On a Vertex-Edge Marking Game on Graphs

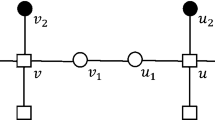
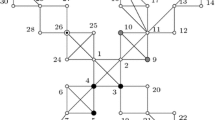
Abstract

The study of a variation of the marking game, in which the first player marks vertices and the second player marks edges of an undirected graph was proposed by Bartnicki et al. (Electron J Combin 15:R72, 2008). In this game, the goal of the second player is to mark as many edges around an unmarked vertex as possible, while the first player wants just the opposite. In this paper, we prove various bounds for the corresponding graph invariant, the vertex-edge coloring number ${\text {col}}_\mathrm{ve}(G)$ of a graph G. In particular, every (finite or infinite) graph G whose edges can be oriented in such a way that the maximum out-degree is bounded by an integer d has ${\text {col}}_\mathrm{ve}(G)\le d+2$. We investigate this invariant in (classes of) planar graphs, including some infinite lattices. We present a close connection between the vertex-edge coloring number of a graph G and the game coloring number of the subdivision graph S(G). In our main result, we bound the vertex-edge coloring number in complete graphs from below and from above, and while ${\text {col}}_\mathrm{ve}(K_n)\le \lceil \log _2{n}\rceil +2$, the difference between the upper and the lower bound is roughly $\log _2(\log _2 n)$. The latter results are, in fact, true for any multigraph whose underlying graph is $K_n$.