Branching Geodesics in Sub-Riemannian Geometry

A metric space is branching if there exist minimal geodesics starting from the same point which follow the same path for some initial time interval, and then become disjoint. Common examples are found in Finsler geometry (e.g. \({\mathbb {R}}^2\) with the sup norm), or on graphs. On the other hand, it is well-known that Riemannian manifolds and Alexandrov spaces with curvature bounded from below are non-branching.

We are interested here in sub-Riemannian spaces, a large class of metric structures generalizing Riemannian geometry where a metric is defined only on a subset of tangent directions (cf. Sect. 2 for precise definitions). Several questions concerning geodesics, which are trivial in Riemannian geometry, become hard open problems in the sub-Riemannian setting. For example it has been only recently proven in [HLD16] that sub-Riemannian geodesics cannot have corners, but it is not yet known whether geodesics are \(C^1\), see for example [Rif17].

To provide further motivation for our contribution, let us mention that there is an on-going effort in trying to define a suitable concept of lower curvature bound for sub-Riemannian spaces, in particular in relation with the synthetic approach à la Lott–Sturm–Villani (cf. for example [BR19, BKS18, BKS19, BG17, Mil19] and [Vil19, p. 1127–1143]). Since the existence of branching geodesics causes difficulties in the study of optimal transport and of spaces satisfying synthetic curvature bounds, it is important for further progress in the theory to understand whether sub-Riemannian structures can exhibit such a phenomenon.

In this paper we show that sub-Riemannian (normal) geodesics can branch, adding this phenomenon to the list of remarkable features of sub-Riemannian geometry. Even though normal geodesics are obtained through the action of a Hamiltonian flow, and are therefore smooth, they are not uniquely characterized by their jet at some point. To our best knowledge, it is the first time that this fact is observed.

1.1 Branching and magnetic fields.

We describe succinctly the branching phenomenon through an example, of the same basic type as Montgomery’s original construction of abnormal minimizers. We will exploit the connection between the equations of motion of a particle in a magnetic field and sub-Riemannian geodesics, pointed out in [Mon90, Mon94].

Take the distribution on \({\mathbb {R}}^3\) defined by the kernel of a one-form \(\omega = dz-A(x,y)dy\), and consider the sub-Riemannian metric given by the restriction of \(dx^2+dy^2\). Let \(B = \partial _x A\) be the magnetic field associated with \(\omega \), that is \(\omega \wedge d\omega = -B(x,y)dx\wedge dy\wedge dz\). Notice that, without changing B, we can alter A in such a way that \(A(0,y)=0\) (gauge freedom), and thus the straight line \(\gamma _0(t) = (0,t,0)\) for \(t\in {\mathbb {R}}\) is horizontal.

It is well-known that abnormal paths are precisely the horizontal curves contained in the zero-locus of B, while normal geodesics are those whose projection (x(t), y(t)) on the xy-plane satisfies

for some \(\lambda \in {\mathbb {R}}\), and where \(\kappa (t)\) is the curvature of (x(t), y(t)), which we assume to be parametrized with constant speed. In particular, the ODE corresponding to (1) describes the motion of a particle with charge \(\lambda \) under the action of the magnetic field B(x, y) normal to the plane.

Choose a smooth potential A(x, y) such that \(B(x,y)=x\) for \(y<0\) and \(B(0,y)>0\) when \(y>0\). The zero-locus of B coincides in this case with \(x=0\) when \(y<0\). In particular, \(\gamma _0(t) = (0,t,0)\), for \(t<0\), is an abnormal geodesic. Since \(B(0,y)=0\) for \(y<0\), the curve \(\gamma _0(t)\) for \(t<0\) satisfies also (1) for any \(\lambda \in {\mathbb {R}}\), so it is also normal. We can now extend such a curve to a normal geodesic \(\gamma _\lambda (t)\) for \(t \in {\mathbb {R}}\), by solving (1) for different values of \(\lambda \in {\mathbb {R}}\). Of course, \(\gamma _0\) corresponds to the straight line but, from the fact that \(B(0,y)>0\) for \(y>0\), the curve \(\gamma _\lambda \) must have non-vanishing curvature for small non-zero \(\lambda \), hence a branching phenomenon occurs at the origin. Moreover, from what we will show in Proposition 11, the projection on the xy-plane of the trajectories \(\gamma _{\lambda }\) contains an open neighborhood of the positive y-axis and those trajectories are all distinct for \(\lambda \) sufficiently small. From the physical viewpoint, this phenomenon corresponds to particles having different charges, which “spray out” following different trajectories under the influence of the magnetic field.

In Sect. 4, we show an explicit construction of such A(x, y), obtained by gluing a flat Martinet structure with the standard Heisenberg one.

1.2 Strictly abnormal branching.

In this note we only consider the branching of normal geodesics, and we do not cover the possible branching of strictly abnormal ones (cf. Sect. 2). It is easy to produce sub-Riemannian structures with branching abnormal paths. For example, consider a degenerate Martinet-type structure in a three-dimensional space, whose Martinet surface itself branches. Such a structure cannot verify the usual non-degeneracy condition, cf. [Mon02, Sec. 3.2]. The Liu–Sussmann local minimality result for abnormal paths does not apply [LS95], and we are not able to prove that these paths are geodesic (i.e. length-minimizing curves).

Open problem

Find an example of branching strictly abnormal geodesics.

1.3 Structure of the paper.

To make the paper self-contained, in Sect. 2 we recall some basic facts in sub-Riemannian geometry, following [ABB19]. Sub-Riemannian branching is then discussed in Sect. 3, and put in relation with the well-known normal/abnormal duality of sub-Riemannian geodesics. The explicit construction of an example, as described in the abstract, is done in Sect. 4. We conclude by building the most general case of multiply-branching normal geodesics, in Sect. 5.

A sub-Riemannian structure on a smooth n-dimensional manifold M, where \(n\ge 2\), is defined by a set of m global smooth vector fields \(X_{1},\ldots ,X_{m}\), called a generating frame. The distribution is the possibly rank-varying family of subspaces of the tangent spaces spanned by the vector fields at each point

The generating frame induces an inner product \(g_{x}\) on \({\mathcal {D}}_{x}\) such that

We assume that the structure is bracket-generating, i.e., the tangent space \(T_{x}M\) is spanned by the vector fields \(X_{1},\ldots ,X_{m}\) and their iterated Lie brackets at x.

A horizontal curve \(\gamma : [0,1] \rightarrow M\) is an absolutely continuous path such that there exists a control \(u\in L^{2}([0,1],{\mathbb {R}}^{m})\) satisfying

This implies that \({{\dot{\gamma }}}(t) \in {\mathcal {D}}_{\gamma (t)}\) for almost every t. Notice that the control u in (2) is not unique, but one can always find a unique minimal control, i.e. the one such that \(g_x({{\dot{\gamma }}}(t),{{\dot{\gamma }}}(t)) = |u(t)|^2\) for a.e. \(t\in [0,1]\). We define the length of \(\gamma \) as

The sub-Riemannian (or Carnot–Carathéodory) distance is defined by:

By the Chow–Rashevskii theorem, under the bracket-generating assumption, between any two points \(x,y\in M\), there exists a horizontal path, and therefore the sub-Riemannian distance is well-defined. Furthermore, one can prove that it is continuous and its induced topology is the same as the manifold topology. We remark that this definition of sub-Riemannian metric, based on the concept of global generating frame, includes the classical constant-rank case, see [ABB19, Section 3.1.4].

In place of the length, it is convenient to consider the energy

Horizontal trajectories minimizing the energy with fixed endpoints are exactly paths that minimize the length, parametrized with constant speed. We call a minimizing geodesic between two points x and y in M a horizontal path \(\gamma :[0,1]\rightarrow M\), with \(\gamma (0)=x\) and \(\gamma (1)=y\), that minimizes the energy among all horizontal paths sharing the same extremities. The term geodesic, instead, denotes the more general class of horizontal paths that are minimizing geodesics locally around each of its points.

2.1 Characterization of geodesics.

Let \(x\in M\). By Cauchy–Lipschitz, there exists an open set \({\mathcal {U}} \subseteq L^2([0,1],{\mathbb {R}}^m)\) such that, for all \(u \in {\mathcal {U}}\), the Cauchy problem:

admits a solution \(\gamma _u\) defined on [0, 1]. The end-point map \(E_x : {\mathcal {U}} \mapsto M\) is then \(E_x(u) = \gamma _u(1)\). The end-point map is weakly continuous and differentiable. The problem of finding a minimizing geodesic between two points x and y is then the problem of minimizing the functional J (seen as a smooth functional defined on \({\mathcal {U}}\)) under the constraint \(E_x(u)=y\). By the Lagrange’s multipliers rule, if \(\gamma \) is a minimizing geodesic between x and y, and u is its minimal control, then there exists \(\lambda _1 \in T_y^*M\) and \(\nu \in \{0,1\}\), with \((\lambda _1,\nu ) \ne 0\), such that

where \(\circ \) denotes the composition of linear maps and D the (Fréchet) differential. Any path whose minimal control verifies (3) with \(\nu =0\) is called abnormal, or singular. A path verifying (3) for its minimal control with \(\nu =1\) is called normal. Notice that the case \(\nu =0\) means that u is a critical point of the end-point map.

The covector \(\lambda _1\) can be interpolated for times \(t \in [0,1]\) yielding a lift of the curve \(\gamma \) in the cotangent bundle. In particular in the normal case, the lift \(\lambda : [0,1]\rightarrow T^*M\) solves a Hamiltonian differential equation. To state this fact more precisely, let us first define some objects: if X is a vector field on M, we can associate to it a function \(h_{X} : T^{*}M \rightarrow {\mathbb {R}}\) defined by \(h_{X}(\lambda )=\langle \lambda ,X \rangle \). In turn, if h is a function on the cotangent bundle, its associated vector field \(\vec {h}\) is defined by \(\sigma (\cdot ,\vec {h})=dh\), where \(\sigma \) is the canonical symplectic form on the cotangent bundle, which can be expressed in coordinates as \(\sigma = \sum _{i=1}^{n}dp_i \wedge dq_i\). Finally, for a sub-Riemannian structure in M given by a generating family as above, we define the Hamiltonian \(H: T^*M \rightarrow {\mathbb {R}}\) by

The following result is an immediate consequence of the characterization of energy minimizers by the Lagrange multipliers rule, or can also be seen as a version of the Pontryagin maximum principle in this setting, cf. [AS04].

Theorem 1

Let \(\gamma \) be a horizontal path minimizing the energy between x et y, and let u be its minimal control. Then there exists a Lipschitz path \(\lambda : [0,1] \rightarrow T^* M\) lifting \(\gamma \)—that is for all \(t \in [0,1]\), \(\lambda (t) \in T_{\gamma (t)}^*M\)—such that

Moreover, one of those two conditions is verified:

1. (N)

   for all \(t \in [0,1]\) and all \(i=1,\dots ,m\), it holds \(u_i(t)=h_{X_i}(\lambda (t))\), that is \(\lambda \) is solution of the differential equation \({\dot{\lambda }}(t)=\vec {H}(\lambda (t))\);

2. (A)

   for all \(t \in [0,1]\) and all \(i =1,\dots ,m\), it holds \(h_{X_i}(\lambda (t))=0\) and \(\lambda (t) \ne 0\).

The conditions (N) and (A) correspond to the normal and abnormal cases of Lagrange multipliers rule, with \(\lambda (1)\) corresponding to the multiplier \(\lambda _1\) in (3).

Remark 2

From (3) the set of normal Lagrange multipliers of a path is an affine space over the linear space generated by its abnormal ones. The same property holds for the corresponding lifts.

The Hamiltonian characterization in the normal case allows us to define an exponential map \(\exp _x : T_x^* M \rightarrow M\), where \(\exp _x(\lambda )=\pi \circ e^{\vec {H}}(\lambda )\), where \(t \mapsto e^{t\vec {H}}\) denotes the one-parameter group of diffeomorphisms on the cotangent bundle given by the Hamiltonian flow. In other words \(\exp _x(\lambda )\) is the extremity at time 1 of the normal geodesic whose lift verifies \(\lambda (0)=\lambda \), that is parametrized by constant speed equal to \(\sqrt{2H(\lambda )}\). Normal paths are locally length minimizing, and hence are geodesics. We assume that \((M,d_{SR})\) is complete, so that \(\vec {H}\) is a complete vector field.

Note that if a path is normal (resp. abnormal), any smaller segment is also normal (resp. abnormal) as the restriction of the lift verifies the same conditions.

The lift of a minimizing path given by Theorem 1 is not necessarily unique and therefore the same horizontal path can be normal and abnormal at the same time. We will call a path strictly normal if it is normal and it does not admit an abnormal lift, and strictly abnormal if it is abnormal and it does not admit a normal lift.

As a final remark, if a path is strictly normal, then its normal lift is unique. Indeed, if \(\lambda \) and \(\mu \) were two distinct normal lifts, then \(\lambda (1)-\mu (1)\) would be an abnormal multiplier for this path (cf. Remark 2).

A natural question is whether strictly normal paths can contain non-trivial abnormal subsegments. We will first show that this behaviour is linked to the occurrence of branching normal geodesics, and moreover that such an occurrence is actually equivalent to a jump in the rank of the differential of the end-point map. Then, in the next section, we will show a simple and natural example of this phenomenon.

First let us define precisely what we will call branching here.

Definition 3

A normal geodesic \(\gamma \) is branching at time \(t\in (0,1)\) if there exists a normal geodesic \(\gamma '\) such that \(\gamma |_{[0,t]}=\gamma '|_{[0,t]}\) and \(\gamma |_{[0,t+\varepsilon ]} \ne \gamma '|_{[0,t+\varepsilon ]}\) for all \(\varepsilon >0\).

Let \(\gamma \) be a normal geodesic. For \(t \in [0,1]\) we define the set

This set is a non-empty affine space corresponding to the initial normal covectors of the path \(\gamma |_{[0,t]}\) given by Theorem 1. The set \(\Pi _t\) is an isomorphic image of the set of normal Lagrange multipliers of \(\gamma |_{[0,t]}\) and, from Remark 2, its dimension is the corank of the path \(\gamma |_{[0,t]}\), defined as the corank of the application \(D_{u_t}E_x\), where \(u_t\) is the minimal control of \(\gamma |_{[0,t]}\). The function \(t \mapsto \Pi _t\) for \(t \in [0,1]\) is nonincreasing for the inclusion order and it is thus piecewise constant with some possible jumps where its dimension decreases.

Definition 4

The corank function of \(\gamma \) is the function that associates to a time \(t \in [0,1]\) the corank of \(\gamma |_{[0,t]}\), that is the function \(t \mapsto \dim \Pi _t\). We say that \(\gamma \) is rank-jumping (or corank-jumping) at time t if there is a discontinuity in the corank function for this time.

The corank function is nonincreasing and piecewise constant and moreover, from the lower semicontinuity of the rank and the \(C^1\) regularity of the end-point map, it is left-continuous. We say that \(\gamma \) is rank-jumping (or corank-jumping) at time t if there is a discontinuity in the corank function for this time.

We can now state our theorem linking the phenomenon of branching normal geodesics with rank jumps, which at this point is very elementary to prove.

Theorem 5

A normal geodesic \(\gamma \) branches at time \(t \in (0,1)\) if and only if it is rank-jumping at time t.

Proof

Assume \(\gamma \) branches at time t. Then the branching geodesic \(\gamma '\) has an initial covector \(\lambda '\) such that \(\lambda ' \in \Pi _t\) but \(\lambda '\notin \Pi _{t+\varepsilon }\) for all \(\varepsilon >0\), which means the rank jumps at t. Conversely, if the rank jumps at time t, there is a covector \(\lambda '\) in \(\Pi _t\) that is not contained in \(\Pi _s\) for \(s>t\), and the path \(\gamma '\) defined by \(\gamma '(t)=\pi \circ e^{t\vec {H}}(\lambda ')\) branches with \(\gamma \) at time t. \(\square \)

An immediate consequence is that a normal path can only branch a finite amount of times (up to the maximal corank of a path, which is the corank of the distribution), and furthermore \(\gamma |_{[0,t]}\) must be abnormal.

If \(\gamma \) is strictly normal, its corank is 0 and we have the following corollary, corresponding to the situation encountered in the example from next section.

Corollary 6

A strictly normal geodesic \(\gamma \) is branching for some time \(t \in (0,1)\) if and only if it contains a non-trivial abnormal subsegment that starts at time 0. In particular if t is the last branching time, \(\gamma |_{[0,t]}\) is a maximal abnormal subsegment.

In this situation, if \(\gamma \) branches at time \(t\in (0,1)\), then it branches in a whole family of distinct normal paths, parametrized by the abnormal Lagrange multipliers of the abnormal subsegment. To be more precise, let \(A \subset T_{\gamma (t)}^*M\) be the set of abnormal Lagrange multipliers associated with the maximal abnormal subsegment \(\gamma |_{[0,t]}\). Notice that \(A \cup \{0\}\) is a vector space, and its dimension is the corank of the abnormal path \(\gamma |_{[0,t]}\). Let \(\lambda \) be the unique normal lift of \(\gamma \). Then for all \(\alpha \in A \cup \{0\}\) the family of curves

is a smooth family of normal geodesics, all coinciding with \(\gamma \) on the subinterval [0, t], and branching from it at time t.

We know that each of the paths in this family is locally minimizing since they are normal. Moreover, if we take a compact subfamily of those, the time at which they are minimizing, starting from the branching point, can be chosen uniformly.

Theorem 7

Let \(\gamma _\alpha \) be a family of normal paths branching from \(\gamma \) at time \(t\in (0,1)\), as in (4). Then for any compact subset \(A_0 \subset A \cup \{0\}\) there exists \(\varepsilon >0\) such that \(\gamma _a|_{[t-\varepsilon ,t+\varepsilon ]}\) is the unique length-minimizing path between its extremities, up to reparametrizations, for all \(\alpha \in A_0\).

The proof of Theorem 7 is a small adaptation of the proof for a single normal path, and it is an immediate consequence of the following more general result.

Proposition 8

Let \(x\in M\), and let \(\Lambda \subset T_{x}^*M\) be a compact set. For \(\lambda \in \Lambda \), consider the normal paths \(\gamma ^{\lambda }(t)=\pi \circ e^{t\vec {H}}(\lambda )\). Then there exists \(\varepsilon >0\) such that, for all \(\lambda \in \Lambda \), the restriction \(\gamma ^{\lambda }|_{[-\varepsilon ,\varepsilon ]}\) is the unique length-minimizing path between its extremities, up to reparametrizations.

Proof

We want to apply the following obvious extension of [ABB19, Corollary 4.64].

Lemma 9

Let \(T>0\) and \(a \in C ^{\infty }(M)\). Let \(\Omega _0\) be an open subset of M such that, for all \(t \in [-T,T]\), the map \(\pi \circ e^{t \vec {H}} \circ da|_{\Omega _0}\) is a diffeomorphism from \(\Omega _0\) on its image \(\Omega _t\). Let \(\lambda _0 \in {\mathcal {L}}_0 \cap \pi ^{-1}(\Omega _0)\) where \({\mathcal {L}}_0=\{d_z a \mid z\in M \}\) and define \({\bar{\gamma }}(t) = \pi \circ e^{t \vec {H}}(\lambda _0)\), for \(t \in [-T,T]\). Then \({\bar{\gamma }}\) is the unique length-minimizing path, up to reparametrization, among all horizontal paths \(\gamma : [-T,T] \rightarrow M\) with the same extremities and such that \(\gamma (t) \in \Omega _t\) for all \(t \in [-T,T]\).

To do it, for \(\lambda \in \Lambda \), we construct a family of functions \(a^{\lambda }\), continuous with respect to \(\lambda \) such that \(d_{x}a^{\lambda }=\lambda \). Indeed, the theorem being a local result, we can suppose to be in a coordinates system \((x_1,\dots ,x_n)\) on a neighborhood of x, and if \(\lambda =\sum _{i=1}^{n} \lambda _i dx_i\), we define \(a^{\lambda }(x_1,\dots ,x_n)=\sum _{i=1}^{n} \lambda _i x_i\).

Let \(\Omega _0\) be a relatively compact neighborhood of x which, for small T, contains \(\gamma ^{\lambda }|_{[-T,T]}\) for all \(\lambda \in \Lambda \). Consider the maps \(\phi _{t}^{\lambda }=\pi \circ e^{t \vec {H}} \circ da^\lambda |_{\Omega _0}\), for \(t \in [-T,T]\) and \(\lambda \in T_{x}^*M\), noting that they are continuous in t and \(\lambda \). For all \(\lambda \in \Lambda \), we have \(\phi _0^{\lambda }=\mathrm {Id}|_{\Omega _0}\), so by semi-continuity of the rank, and by the fact that \({\overline{\Omega }}_0\) is compact, there exists a neighborhood of \(\{0\} \times {\Lambda }\) where \(d_x\phi _{t}^{\lambda }\) in an isomorphism. By compactness of \(\Lambda \), this neighborhood contains a set of the form \([-t_0,t_0] \times \Lambda \). By the inverse function theorem, and up to reducing \(\Omega _0\), \(\phi _{t}^{\lambda }\) is a diffeomorphism on its image for all \((t,\lambda ) \in [-t_0,t_0] \times \Lambda \). Indeed, by compactness, the neighborhood of x given by the inverse function theorem can be uniformly chosen for \((t,\lambda ) \in [-t_0,t_0] \times \Lambda \), by using a quantitative version of the latter, see [Rif14, Theorem B.1.4].

Let \(K_1 \subset \Omega _0\) be a compact neighborhood of x. By continuity, there exists a neighborhood of \(\{0\} \times \Lambda \) such that \(K_1 \subset \Omega _t^\lambda =\phi _{t}^{\lambda }(\Omega _0)\) for all \((t,\lambda )\) in this neighborhood. Since \(\Lambda \) is compact, we get \(t_1 \in (0,t_0]\) such that \(K_1 \subset \Omega _t^{\lambda }\) for all \(t\in [-t_1,t_1]\) and all \(\lambda \in \Lambda \). Let then \(K_2\) be a compact neighborhood of x included in the interior of \(K_1\) and we find \(t_2 \in (0,t_1]\) such that \(\gamma ^{\lambda }(t) \in {K_2}\) for all \(\lambda \in \Lambda \) and all \(t \in [-t_2,t_2]\). Finally, let us pose \(\delta = d_{SR}(K_2,M \setminus K_1) >0\), and

Let \(\lambda \in \Lambda \) and \(\gamma \) be a horizontal path defined for \([-\varepsilon ,\varepsilon ]\) such that \(\gamma (-\varepsilon )=\gamma ^{\lambda }(-\varepsilon )\) and \(\gamma (\varepsilon )=\gamma ^{\lambda }(\varepsilon )\), but whose image \(\Gamma \) is distinct from the image of \(\gamma ^{\lambda }\). If \(\Gamma \subset K_1\), then \(\gamma (t) \in \Omega _t^{\lambda }\) for all t, and we can thus apply Lemma 9 to conclude that \(\ell (\gamma )>\ell (\gamma ^{\lambda }|_{[-\varepsilon ,\varepsilon ]})\). Otherwise, there exists \(t^*\in [-\varepsilon ,\varepsilon ]\) such that \(\gamma (t^*) \notin K_1\). Then, since \(\gamma (-\varepsilon ) \in K_2\), we have:

\(\square \)

Let us stress that normal geodesics cannot branch in real-analytic sub-Riemannian structures, that is when the corresponding Hamiltonian function is real-analytic. In fact in this case, by the Cauchy–Kowalevski theorem, normal geodesics, which are projections of the solutions of the Hamiltonian equation, are real-analytic paths. By the principle of permanence, two distinct real-analytic paths cannot be equal on a segment. That is, the following well-known fact holds:

Proposition 10

If H is real-analytic, normal geodesic cannot branch.

For building an example, we need to find a smooth, but non real-analytic structure, in which there is an abnormal geodesics that becomes strictly normal. A natural idea is to start from a structure admitting non-trivial abnormal geodesics (the simplest example being the flat Martinet structure) and “glue” it to a structure that do not admit non-trivial abnormal paths, like the Heisenberg structure. In fact, this works exactly as stated, and this is the idea that led us to the discovery of branching geodesics.

Let \(\theta : {\mathbb {R}}\rightarrow [0,1]\) be a smooth non-decreasing function such that \(\theta (t)=0\) if \(t\le 0\), \(\theta (t)>0\) if \(t>0\), and \(\theta (t)=1\) if \(t \ge 1\). Let \(A(x,y)=x\theta (y) + x^2 \theta (1-y)\). Consider a rank 2 sub-Riemannian structure on \({\mathbb {R}}^3\) defined by the following vector fields:

so that we have a flat Martinet structure on the half-space \(y \le 0\) and a Heisenberg one for \(y \ge 1\). The Lie bracket between those vector fields is:

so that \({{\,\mathrm{span}\,}}\{X,Y,[X,Y]\}= {\mathbb {R}}^3\), except on the so-called Martinet surface

At all points in \(\Sigma \), we have \([X,[X,Y]] = 2 \theta (1-y) \partial _z \ne 0\), therefore \(\Sigma \) is smooth and the distribution is bracket-generating. It is well-known that abnormal paths for this distribution are exactly the horizontal ones contained in \(\Sigma \), see for example [Mon02, Rif14]. To characterize normal geodesics, the Hamiltonian function is

The Hamiltonian vector field is thus, in coordinates \((x,y,z,p_x,p_y,p_z)\):

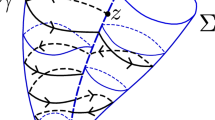
In particular, the path in the cotangent bundle (0, t, 0, 0, 1, 0), for \(t \in {\mathbb {R}}\) is an integral curve of \(\vec {H}\), and therefore the lift of the normal geodesic \(\gamma (t) = (0,t,0)\). For \(t<0\), its projection \(\gamma \) is contained in the Martinet surface \(\Sigma \), and therefore this part of the curve is abnormal. Indeed, for every \(\alpha \ne 0\), the path \((0,t,0,0,0,\alpha )\) is an abnormal lift of this geodesic. As soon as \(t>0\), however, \(\gamma \) is not contained in \(\Sigma \) and therefore any such a segment is strictly normal. It is quite natural for this to happen as the Heisenberg structure has no abnormal geodesics. So if we consider the path \(\gamma (t)=(0,t,0)\) for \(t \in [-T,T]\) for some \(T>0\), it has a maximal abnormal subsegment \([-T,0]\) and therefore by Corollary 6, it branches at time \(t=0\).

What happens is that, starting at \(t=-T\) and until \(t=0\), the differential of the end-point map has a 1-dimensional cokernel for the corresponding control, which is the family of covectors \((0,0,\alpha )\) for \(\alpha \in {\mathbb {R}}\), and thus the space of initial covectors of normal lifts for this path is the 1-dimensional affine space \(\{(0,1,\alpha )\mid \alpha \in {\mathbb {R}}\}\). Once time \(t=0\) is attained the abnormal geodesic can still be prolonged (as the trace of the distribution in \(\Sigma \)) but it loses its normal status, becoming strictly abnormal. Meanwhile, the 1-dimensional family of normal lifts can be prolonged yielding a family of distinct geodesics, which are all strictly normal. In Fig. 1 we computed, using the Euler method, some of those geodesics \(\gamma _\alpha \), for different values of \(\alpha \).

Numerical plot of the branching geodesics \(\gamma _\alpha \), projected on the xy plane. Notice that the abnormal path lies in the Martinet surface, which must bend in order to avoid the Heisenberg region.

Full size image

Finally, we observe that the collection of those normal geodesics do describe an embedded surface of \({\mathbb {R}}^3\), at least locally around the y-axis (which is the normal geodesic with initial covector (0, 1, 0)) as shown in this result:

Proposition 11

The map \(\Phi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^3\) defined by \(\Phi (t,\alpha )=\pi \circ e^{(t+T)\vec {H}}(\lambda _\alpha )\), where \(\lambda _{\alpha }\) is the initial covector \((0,1,\alpha )\) at point \((0,-T,0)\), is an embedding on a neighborhood of any point (t, 0) with \(t>0\).

Proof

Since \(\Phi (t,0) = (0,t,0)\), we have \(\frac{\partial \Phi }{\partial t} (t,0) = \partial _y\). So we just have to show that \(\frac{\partial \Phi }{\partial \alpha } (t,0)\) is independent from \(\partial _y\), which we will do by pointing out that its x component is non zero. Let

be the solution of Hamilton’s equation (5), with initial condition \((0,-T,0,0,1,\alpha )\) at time \(t=0\), in such a way that \(\Phi (t,\alpha ) = (x^\alpha (t),y^\alpha (t),z^\alpha (t))\). We observe that \(p_z^{\alpha }(t) = \alpha \) for all times, and thus:

Here \(f(\alpha ,\tau )\) is a smooth function whose expression can be obtained from (5). We notice only that \(f(0,\tau )=\theta (\tau )\). So

which is non-zero by the properties of \(\theta \). \(\square \)

Remark 12

As anticipated in Sect. 1.1, any smooth A such that \(A(0,y)=0\), and such that \(B=\partial _x A\) satisfies \(B(x,y) =x\) for \(y<0\), and \(B(0,y)>0\) when \(y>0\), yields a one-parameter family of branching geodesics, verifying Proposition 11.

In the example from the previous section, the corank function of a path \(\gamma _{\alpha }\) starting at \(t=-T\) is equal to one for \(t\le 0\) and zero for \(t>0\). From this, we can easily construct any kind of corank function, and therefore any kind of normal branching. To do that, we consider a suitable product of our example.

The product \(M_1 \times M_2\) of sub-Riemannian manifolds \(M_1\) and \(M_2\) has a product sub-Riemannian structure simply defined as the direct sum of the distributions and the metrics in \(M_1\) and \(M_2\). It is then easy to see that a path \(\gamma \) is a geodesic in M if and only if \(\gamma _1\) and \(\gamma _2\) are geodesics in \(M_1\) and \(M_2\), where \(\gamma _i\) is the projection of \(\gamma \) on \(M_i\). Moreover, if \(\lambda _1\) and \(\lambda _2\) are normal Lagrange multipliers for \(\gamma _1\) and \(\gamma _2\) respectively, \((\lambda _1,\lambda _2)\) is a normal Lagrange multiplier for \(\gamma \), and the converse is true. The same is true for abnormal multipliers, so the corank of a path \(\gamma \) is the sum of the coranks of the \(\gamma _i\). From these observations, we get the following result, which gives a complete description of what kind of branching one can expect:

Theorem 13

Let \(f:[0,1] \rightarrow {\mathbb {N}}\) be a nonincreasing left-continuous function. Then there exists a sub-Riemannian manifold M and a normal geodesic \(\gamma \) on M such that its corank function coincides with f. In particular \(\gamma \) branches at the jumps of f.

Proof

Constant paths have corank equal to the corank of the distribution, therefore the corank of M must be equal to f(0). So we define M as the sub-Riemannian product \(M=N^{f(0)}\), where N is the sub-Riemannian structure in \({\mathbb {R}}^3\) defined in Sect. 4. Denote then by \(a=f(0)-f(0^+)\) (\(f(0^+)\) being the right limit of f at 0), \(b=f(1)\) and \(t_1,\dots ,t_k\) the times of the discontinuities of f in (0, 1), each one repeated multiple times according to the amplitude of the discontinuity. Denote as previously by \(\gamma \) the path in N defined by \(\gamma (t)=(0,t,0)\) for \(t\in {\mathbb {R}}\) and take \(\gamma _0\) any strictly normal geodesic with no non-trivial abnormal subsegments in N (for example \(\gamma _0=\gamma |_{[0,1]}\)).

If we define the path \({\tilde{\gamma }} : [0,1] \rightarrow M\) by:

then the corank function of \({\tilde{\gamma }}\) is exactly f.

As a remark, we also have a full description of the normal geodesics branching from \({\tilde{\gamma }}\), given, for \(\alpha _1,\dots ,\alpha _k \in {\mathbb {R}}\), by:

where \(\gamma _{\alpha }\) are the already defined branching geodesics in N, from Sect. 4. \(\square \)