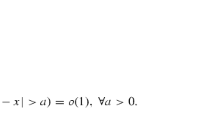Abstract
We study the limit distribution of partial sums with a random number of terms following a class of mixed Poisson distributions. The resulting weak limit is a mixture between a normal distribution and an exponential family, which we call by normal exponential family (NEF) laws. A new stability concept is introduced and a relationship between \(\alpha \)-stable distributions and NEF laws is established. We propose the estimation of the NEF model parameters through the method of moments and also by the maximum likelihood method via an Expectation–Maximization algorithm. Monte Carlo simulation studies are addressed to check the performance of the proposed estimators, and an empirical illustration of the financial market is presented.






Similar content being viewed by others
References
Azzalini A (1985) A class of distributions which includes the normal ones. Scand J Stat 12:171–178
Abramowitz M, Stegun IA (1965) Handb Math Funct. Dover Publications, New York
Barndorff-Nielsen OE (1997) Normal inverse Gaussian distributions and stochastic volatility modelling. Scand J Stat 24:1–13
Barndorff-Nielsen OE, Kent J, Sørensen M (1982) Normal variance-mean mixtures and z distributions. Int Stat Rev 50:145–159
Barreto-Souza W (2015) Long-term survival models with overdispersed number of competing causes. Comput Stat Data Anal 91:51–63
Barreto-Souza W, Simas AB (2016) General mixed Poisson regression models with varying dispersion. Stat Comput 26:1263–1280
Bening VE, Korolev VYu (2005) On an application of the student distribution in the theory of probability and mathematical statistics. Theory Prob Appl 49:377–391
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B 39:1–38
Embrechts P, Kluppelberg C, Mikosch T (2003) Modell Extrem Events Insur Finance. Springer, Berlin
Feller W (1971) An introduction to probability theory and its applications, 2nd edn. Wiley, New York
Gavrilenko SV, Korolev VYu (2006) Convergence rate estimates for mixed Poisson random sums. Sistemy i Sredstva Informatiki. special issue pp 248–257
Gnedenko BV, Korolev VYu (1996) Random summation: limit theorems and applications. CRC Press, Boca Raton
Gut A (2013) Probability: a graduate course. Springer, New York
Kalashnikov V (1997) Geometric sums: bounds for rare events with applications. Kluwer Acad. Publ, Dordrecht
Karlis D, Xekalaki E (2005) Mixed Poisson distributions. Int Stat Rev 73:35–58
Korolev VY (1999) On convergence of distributions of compound Cox processes to stable laws. Theory Prob Appl 43:644–650
Korolev VY, Shevtsova IG (2012) An improvement of the Berry–Esseen inequality with applications to Poisson and mixed Poisson random sums. Scand Actuar J 2012:81–105
Korolev VY, Zeifman AI (2016) On convergence of the distributions of random sequences with independent random indexes to variance-mean mixtures. Stoch Models 32:414–432
Korolev VY, Zeifman AI (2016) On normal variance-mean mixtures as limit laws for statistics with random sample sizes. J Stat Plann Inference 169:34–42
Korolev VY, Dorofeeva A (2017) Bounds of the accuracy of the normal approximation to the distributions of random sums under relaxed moment conditions. Lith Math J 57:38–58
Korolev VY, Zeifman A (2019) Generalized negative binomial distributions as mixed geometric laws and related limit theorems. Lith Math J 59:366–388
Kotz S, Kozubowski T, Podgorski K (2001) The Laplace distribution and generalizations: a revisit with applications to communications, economics, engineering, and finance. Springer, Berlin
Kozubowski TJ, Rachev ST (1994) The theory of geometric stable distributions and its use in modeling financial data. Eur J Oper Res 74:310–324
Kruglov VM, Korolev VY (1990) Limit theorems for random sums. Izdatelstvo Moskovskogo Universiteta, Moscow (in Russian)
Louis TA (1982) Finding the observed information matrix when using the EM algorithm. J R Stat Soc Ser B 44:226–233
Mittnik S, Rachev ST (1989) Stable distributions for asset returns. Appl Math Lett 2:301–304
Mittnik S, Rachev ST (1991) Alternative multivariate stable distributions and their applications to financial modeling. Stable Processes and Related Topics pp 107–119
Paulsen J (2008) Ruin models with investment income. Probab Surv 5:416–434
Puig P, Barquinero JF (2010) An application of compound Poisson modelling to biological dosimetry. Proc R Soc A 467:897–910
Rényi A (1956) A characterization of the Poisson process. Translated. In: Turan P (ed) Selected Papers of Alfréd Rényi, vol I. (Akad. Kiado, Budapest, 1976) pp 622–628
Sampson AR (1975) Characterizing exponential family distributions by moment generating functions. Ann Stat 3:747–753
Shevtsova IG (2018) Convergence rate estimates in the global CLT for compound mixed Poisson distributions. Theory Probab Appl 63:72–93
Schluter C, Trede M (2016) Weak convergence to the Student and Laplace distributions. J Appl Prob 53:121–129
West M (1987) On scale mixtures of normal distributions. Biometrika 74:646–648
Acknowledgements
We would like to express our gratitude to the referee for the insightful comments, suggestions, and careful reading which lead to an improvement in the presentation of our paper. G. Oliveira thanks the financial support from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES-Brazil). W. Barreto-Souza acknowledges support for his research from the KAUST Research Fund, NIH 1R01EB028753-01, and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq-Brazil, Grant Number 305543/2018-0). This work is part of the Ph.D. thesis of Gabriela Oliveira realized at the Department of Statistics of the Universidade Federal de Minas Gerais, Brazil.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 2
Consider the change of variable \(W_\phi ^*=\phi W_\phi \). With this, we obtain that the density function of \(W_\phi ^*\) assumes the form (3) with \(\theta =\xi _0\), \(B(\theta )=-\phi b(\theta )\), \(R(y)=-\log \phi +c(y;\phi )\), and support \({\mathbb {S}}={\mathbb {R}}^+\). Then, we use Theorem 1 above to obtain the ch.f. of \(W_\phi ^*\). This immediately gives us the ch.f. of \(W_\phi \) as follows:
From (13), we obtain that
The Tower Property of conditional expectations giwsves
Let \(G_{N_{\lambda }}(\cdot )\) denote the probability generating function of \(N_{\lambda }\). Then, we use (14) to obtain
Taking \(\lambda \rightarrow \infty \) and applying L’Hôpital’s rule twice (in the second-order derivative we are using the assumption of finite variance of \(X_1\)) we obtain
This completes the proof. \(\square \)
Proof of Theorem 3
If Y is MP-stable, then \({\mathcal {D}}(G)\ne \emptyset \). By Lévy’s Continuity Theorem and (15), the convergence in Expression (5) holds if and only if
where \(\varphi _{\lambda }(t) = \varPsi _{X_1}(a_{\lambda }t)\exp (ita_{\lambda }d_{\lambda })\).
The first derivative of the function \(b(\cdot )\) is positive since it is equal to the mean of the exponential family (its support here is assumed to be \({\mathbb {R}}^+\), so that the mean is positive). This implies that \(b(\cdot )\) is strictly monotone increasing and therefore it is invertible. Using this invertibility, it follows that (16) is equivalent to
We can take the limit above with \(\lambda = \lambda _n=n\in {\mathbb {N}}\) instead of \(\lambda \in {\mathbb {R}}\); \(\{\lambda _n\}\) can be seen as a subsequence. In this case, letting \(a_{\lambda }=a_n\) and \(d_{\lambda }=d_n\), it follows that
From Theorem 1 in Chapter XVII in Feller (1971), the above limit implies that
Since the left side of (17) is the ch.f. of
it follows that the right side of that equation is the ch.f. of some \(\alpha \)-stable random variable A [see Theorem 3.1, Chapter 9 in Gut (2013)], say \(\varPsi _A(t)\). Hence, we obtain
which gives us the sufficiency part of the theorem.
Conversely, if (6) holds and \(\varPsi _A(t)\) is the ch.f. of some \(\alpha \)-stable random variable A, then there exist an i.i.d. sequence \(\{X_n\}_{n\in {\mathbb {N}}}\) of random variables and real sequences \(\{a_n\}_{n\in {\mathbb {N}}}\) and \(\{d_n\}_{n\in {\mathbb {N}}}\) such that
Denote by \(\varPsi _{X_1}(t)\) the ch.f. of \(X_1\) and let \(\gamma _{n}(t) = \varPsi _{X_1}(a_n t)\exp (ita_n d_n)\), \(n\in {\mathbb {N}}\). Then, the weak limit in (18) is equivalent to
From Feller (1971), we have that the above limit implies that
Since by hypothesis
we obtain that
which is equivalent to
The above limit gives Eq. (16) with \(\gamma _{\lambda }(t)\) instead of \(\varphi _{\lambda }(t)\). This shows that \({\mathcal {D}}(G)\ne \emptyset \) and the proof is complete. \(\square \)
Proof of Proposition 1
By standard properties of conditional expectation and using the ch.f. of \(W_{\phi }\) given in (13), we obtain that
which is the characteristic function given in Theorem 2. \(\square \)
Proof of Proposition 3
We have that
By using the explicit form of the normal-gamma distribution density given in Expression (8), we get
Denoting \(U \sim \text{ GIG }\left( a, b, p\right) \) with \(a = \frac{\mu ^2}{\sigma ^2} + 2\phi \), \(b = \frac{y^2}{\sigma ^2}\) and \(p = \phi + K - \frac{1}{2}\) and noting that the integrand above is the kernel of a GIG density function, we obtain the desired result. \(\square \)
Proof of Proposition 4
We have that
Let \(f_Y(y)\) be the NIG density function as given in (9) and denote \(U \sim \text{ GIG }\left( a, b, p\right) \) with \(a = \frac{\mu ^2}{\sigma ^2} + \phi \), \(b = \frac{y^2}{\sigma ^2} + \phi \) and \(p = K - 1\). It follows that
This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Oliveira, G., Barreto-Souza, W. & Silva, R.W.C. Convergence and inference for mixed Poisson random sums. Metrika 84, 751–777 (2021). https://doi.org/10.1007/s00184-020-00800-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00184-020-00800-3