On the minimum value of the Colless index and the bifurcating trees that achieve it

Abstract

Measures of tree balance play an important role in the analysis of phylogenetic trees. One of the oldest and most popular indices in this regard is the Colless index for rooted bifurcating trees, introduced by Colless (Syst Zool 31:100–104, 1982). While many of its statistical properties under different probabilistic models for phylogenetic trees have already been established, little is known about its minimum value and the trees that achieve it. In this manuscript, we fill this gap in the literature. To begin with, we derive both recursive and closed expressions for the minimum Colless index of a tree with n leaves. Surprisingly, these expressions show a connection between the minimum Colless index and the so-called Blancmange curve, a fractal curve. We then fully characterize the tree shapes that achieve this minimum value and we introduce both an algorithm to generate them and a recurrence to count them. After focusing on two extremal classes of trees with minimum Colless index (the maximally balanced trees and the greedy from the bottom trees), we conclude by showing that all trees with minimum Colless index also have minimum Sackin index, another popular balance index.

Appendices

Appendices

1.1 A.1 Proof of Proposition 2

Recall that, for every $n \in {\mathbb {N}}_{\geqslant 2}$,

$$\begin{aligned} QB(n):=\big \{ (n_a,n_b)\in {\mathbb {N}}^2\mid n_a\geqslant n_b\geqslant 1,\ n_a+n_b=n, c_{n_a}+c_{n_b}+n_a-n_b=c_n \big \}. \end{aligned}$$

We shall establish the following result.

Proposition 2

For every $n\geqslant 2$ and for every $n_a,n_b\in {\mathbb {N}}_{\geqslant 1}$ such that $n_a\geqslant n_b$ and $n_a+n_b=n$:

• (1) If $n_a=n_b=n/2$, then $(n_a,n_b)\in QB(n)$ always.

• (2) If $n_a>n_b$, then $(n_a,n_b)\in QB(n)$ if, and only if, one of the following three conditions is satisfied:

  • There exist $k\in {\mathbb {N}}$ and $p\in {\mathbb {N}}_{\geqslant 1}$ such that $n=2^k(2p+1)$, $n_a=2^k(p+1)$ and $n_b=2^kp$.

  • There exist $k\in {\mathbb {N}}$, $l\in {\mathbb {N}}_{\geqslant 2}$, $p\in {\mathbb {N}}_{\geqslant 1}$, and $t\in {\mathbb {N}}$, $0\leqslant t<2^{l-2}$, such that $n=2^k(2^l(2p+1)+2t+1)$, $n_a=2^{k+l}(p+1)$, and $n_b=2^{k}(2^lp+2t+1)$.

  • There exist $k\in {\mathbb {N}}$, $l\in {\mathbb {N}}_{\geqslant 2}$, $p\in {\mathbb {N}}_{\geqslant 1}$, and $t\in {\mathbb {N}}$, $0\leqslant t<2^{l-2}$, such that $n=2^k(2^l(2p+1)-(2t+1))$, $n_a=2^k(2^l(p+1)-(2t+1))$, and $n_b=2^{k+l}p$.

The proof of this proposition relies on several auxiliary lemmas. In order to simplify the language in their statements and proofs, throughout this section we systematically assume, without any further notice, that the symbols j, k, m, n, p, s, t, and x, possibly with subscripts or superscripts, always represent natural numbers.

Lemma 7

Let $s=2^ks_0$ with $k\geqslant 1$ and $s_0\geqslant 1$. Then, for every $m\geqslant 1$, $(m+s,m)\in QB(2m+s)$ if, and only if, $m=2^km_0$, for some $m_0\geqslant 1$ such that $(m_0+s_0,m_0)\in QB(2m_0+s_0)$.

Proof

We prove the equivalence in the statement by induction on the exponent $k\geqslant 1$. Recall that, by Remark 2.(b), if $s\geqslant 1$ is even and $c_{m+s}+c_m+s=c_{2m+s}$, then m must be even, too. Therefore, if $s=2t_0$, then $m=2m_1$ for some $m_1\geqslant 1$, and then, since

$$\begin{aligned} c_{2m_1+2t_0}+c_{2m_1}+2t_0=2(c_{m_1+t_0}+c_{m_1}+t_0) \end{aligned}$$

and $c_{4m_1+2t_0}=2c_{2m_1+t_0}$, the equality $c_{m+s}+c_m+s=c_{2m+s}$ is equivalent to the equality $c_{m_1+t_0}+c_{m_1}+t_0=c_{2m_1+t_0}$. This proves the equivalence in the statement when $k=1$.

Now, assume that this equivalence is true for the exponent $k-1$, and let $s=2^ks_0$. Then, by the case $k=1$, $c_{m+s}+c_m+s=c_{2m+s}$ if, and only if, $m=2m_1$ for some $m_1\geqslant 1$ such that

$$\begin{aligned} c_{m_1+2^{k-1}s_0}+c_{m_1}+2^{k-1}s_0=c_{2m_1+2^{k-1}s_0}, \end{aligned}$$

and, by the induction hypothesis, this last equality holds if, and only if, $m_1=2^{k-1}m_0$ for some $m_0\geqslant 1$ such that $c_{m_0+s_0}+c_{m_0}+s_0=c_{2m_0+s_0}$. Combining both equivalences we obtain the equivalence in the statement, thus proving the inductive step. $\square$

Lemma 8

Let $s=2^{j+1}-(2t+1)$ be an odd integer, with $j={\lfloor }\log _2(s){\rfloor }$ and $0\leqslant t<2^{j-1}$. Then, for every $m\geqslant 1$, $(2m+s,2m)\in QB(4m+s)$ if, and only if, $m=2^{j}p$ for some $p\geqslant 1$.

Proof

We prove the equivalence in the statement by induction on s. When $s=1=2^{1}-1$, so that $j=t=0$, the equivalence says that

$$\begin{aligned} c_{2m+1}+c_{2m}+1=c_{4m+1} \end{aligned}$$

for every $m\geqslant 1$, which is true by Corollary 3.

Assume now that the equivalence is true for every odd natural number $s'<s$ and for every m, and let us prove it for $s=2^{j+1}-(2t+1)$ with $0\leqslant t<2^{j-1}$. We have that

$$\begin{aligned} \begin{array}{l} c_{2m+2^{j+1}-2t-1}+c_{2m}+2^{j+1}-2t-1\\ \qquad =\big (c_{m+2^j-t}+c_m+2^j-t\big )+\big (c_{m+2^j-t-1}+c_m+2^j-t-1\big )+1\\ c_{4m+2^{j+1}-2t-1}=c_{2m+2^j-t}+c_{2m+2^j-t-1}+1 \end{array} \end{aligned}$$

and since, by Eq. (2), $c_{m+2^j-t}+c_m+2^j-t\geqslant c_{2m+2^j-t}$ and $c_{m+2^j-t-1}+c_m+2^j-t-1\geqslant c_{2m+2^j-t-1}$, we have that $c_{2m+s}+c_{2m}+s=c_{4m+s}$ if, and only if, the following two identities are satisfied:

$$\begin{aligned}&c_{m+2^j-t}+c_m+2^j-t= c_{2m+2^j-t} \end{aligned}$$

(13)

$$\begin{aligned}&c_{m+2^j-t-1}+c_m+2^j-t-1= c_{2m+2^j-t-1} \end{aligned}$$

(14)

So, we must prove that Eqns. (13) and (14) hold if, and only if, $m=2^{j}p$ for some $p\geqslant 1$. We distinguish two subcases, depending on the parity of t:

• If $t=2x$ for some $0\leqslant x<2^{j-2}$, then Eq. (13) and Lemma  7 imply that m is even, say $m=2m_0$, and then (14) says

  $$\begin{aligned} c_{2m_0+2^j-2x-1}+c_{2m_0}+2^j-2x-1= c_{4m_0+2^j-2x-1}, \end{aligned}$$

  (15)

  which, by induction, is equivalent to $m_0=2^{j-1}p$ for some $p\geqslant 1$, i.e. to $m=2^{j}p$ for some $p\geqslant 1$. So, to complete the proof of the desired equivalence, it remains to prove that if $m=2^{j}p$, then Eq. (13) holds. If $t=0$, this equality says

  $$\begin{aligned} c_{2^{j}p+2^j}+c_{2^{j}p}+2^j=c_{2^{j+1}p+2^j} \end{aligned}$$

  and it is a direct consequence of Lemma  7 and Corollary 3. So, assume that $t>0$ and write it as $t=2^i(2x_0+1)$ with $1\leqslant i<j-1$ and $x_0<2^{j-i-2}$. Then

  $$\begin{aligned}&c_{m+2^j-t}+c_m+2^j-t \\&\quad = c_{2^{j}p+2^j-2^i(2x_0+1)} +c_{2^{j}p}+2^j-2^i(2x_0+1)\\&\quad = 2^i\big (c_{2^{j-i}p+2^{j-i}-2x_0-1}+c_{2^{j-i}p}+2^{j-i}-2x_0-1\big )\\&\quad = 2^ic_{2^{j-i+1}p+2^{j-i}-2x_0-1} \text{(by } \text{ the } \text{ induction } \text{ hypothesis) }\\&\quad = c_{2^{j+1}p+2^{j}-2^i(2x_0+1)}=c_{2m+2^j-t}. \end{aligned}$$

• If $t=2x+1$ for some $0\leqslant x< 2^{j-2}$, then Eq. (14) and Lemma  7 imply that m is even, say $m=2m_0$, and then it is Eq. (13) which becomes Eq. (15) above, which, in turn, by induction is equivalent to $m_0=2^{j-1}p$ for some $p\geqslant 1$, that is, to $m=2^{j}p$ for some $p\geqslant 1$. Thus, to complete the proof of the desired equivalence, it remains to prove that if $m=2^{j}p$, then (14) holds. Now:

  $$\begin{aligned}&c_{m+2^j-t-1}+c_m+2^j-t-1\\&\quad = c_{2^{j}p+2^j-2x-2}+c_{2^{j}p}+2^j-2x-2\\&\quad =2\big (c_{2^{j-1}p+2^{j-1}-x-1}+c_{2^{j-1}p}+2^{j-1}-x-1\big ) \end{aligned}$$

  If x is even, say $x=2x_0$, then, since $x_0<2^{j-3}$, the induction hypothesis implies that

  $$\begin{aligned}&2\big (c_{2^{j-1}p+2^{j-1}-x-1}+c_{2^{j-1}p}+2^{j-1}-x-1\big )\\&\quad =2 c_{2^{j}p+2^{j-1}-x-1} = c_{2^{j+1}p+2^{j}-2x-2}= c_{2m+2^j-t-1}. \end{aligned}$$

  And if x is odd, write it as $x=2^i(2t_0+1)-1$ for some $1\leqslant i<j-1$ (and notice that $x<2^{j-2}$ implies $t_0<2^{j-i-3}$) and then

  $$\begin{aligned}&2\big (c_{2^{j-1}p+2^{j-1}-x-1}+c_{2^{j-1}p}+2^{j-1}-x-1\big )\\&\quad = 2\big (c_{2^{j-1}p+2^{j-1}-2^i(2t_0+1)}+c_{2^{j-1}p}+2^{j-1}-2^i(2t_0+1)\big )\\&\quad =2\cdot 2^i\big (c_{2^{j-i-1}p+2^{j-i-1}-(2t_0+1)}+c_{2^{j-i-1}p}+2^{j-i-1}-(2t_0+1)\big )\\&\quad = 2^{i+1} c_{2^{j-i}p+2^{j-i-1}-(2t_0+1)} \text{(by } \text{ the } \text{ induction } \text{ hypothesis) }\\&\quad = c_{2^{j+1}p+2^{j}-2^{i+1}(2t_0+1)}=c_{2^{j+1}p+2^{j}-2x-2}\\&\quad =c_{2m+2^j-t-1} \end{aligned}$$

  This completes the proof of the desired equivalence when t is odd.

So, the inductive step is true in all cases. $\square$

Lemma 9

Let $s=2^{j+1}-(2t+1)$ be an odd integer, with $j={\lfloor }\log _2(s){\rfloor }$ and $0\leqslant t<2^{j-1}$. Then, for every $m\geqslant 0$, $(2m+1+s,2m+1)\in QB(4m+2+s)$ if, and only if, either $m=2^{j}p+t$ for some $p\geqslant 1$ or $s=1$ (i.e. $j=t=0$) and $m=0$.

Proof

We also prove the equivalence in this statement by induction on s. When $s=1=2^{1}-1$, the equivalence says that $c_{2m+2}+c_{2m+1}+1=c_{4m+3}$ for every $m\geqslant 0$, which is true by Corollary 3.

Assume now that the equivalence is true for every odd natural number $1\leqslant s'<s$ and for every $m\geqslant 0$, and let us prove it for $s=2^{j+1}-(2t+1)\geqslant 3$ with $0\leqslant t<2^{j-1}$. In this case, m cannot be 0, because, by Remark 2.(a), $(s+1,1)\in QB(s+2)$ if, and only if, $s=1$. So, we can consider only the case $m\geqslant 1$. Then, we have that

$$\begin{aligned}&c_{2m+1+2^{j+1}-2t-1}+c_{2m+1}+2^{j+1}-2t-1\\&\quad =\big (c_{m+2^j-t}+c_m+2^j-t\big )+\big (c_{m+2^j-t}+c_{m+1}+2^j-t-1\big )+1\\&c_{4m+2+2^{j+1}-2t-1}=c_{2m+2^j-t}+c_{2m+2^j-t+1}+1 \end{aligned}$$

and since, by Eq. (2), $c_{m+2^j-t}+c_m+2^j-t\geqslant c_{2m+2^j-t}$ and $c_{m+2^j-t}+c_{m+1}+2^j-t-1\geqslant c_{2m+2^j-t+1}$, we have that $c_{2m+1+s}+c_{2m+1}+s=c_{4m+2+s}$ if, and only if,

$$\begin{aligned}&c_{m+2^j-t}+c_m+2^j-t= c_{2m+2^j-t} \end{aligned}$$

(16)

$$\begin{aligned}&c_{m+2^j-t}+c_{m+1}+2^j-t-1=c_{2m+2^j-t+1} \end{aligned}$$

(17)

So, we must prove that Eqns. (16) and (17) hold for $m\geqslant 1$ if, and only if, $m=2^{j}p+t$ for some $p\geqslant 1$. We distinguish again two subcases, depending on the parity of t:

• If $t=2x$ for some $0\leqslant x<2^{j-2}$, then Eq. (16) and Lemma  7 imply that m is even, say $m=2m_0$ with $m_0\geqslant 1$, and then Eq. (17) can be written

  $$\begin{aligned} c_{2m_0+1+2^j-2x-1}+c_{2m_0+1}+2^j-2x-1= c_{4m_0+2+2^j-2x-1} \end{aligned}$$

  which, by induction, is equivalent to $m_0=2^{j-1}p+x$ for some $p\geqslant 1$, that is, to $m=2m_0=2^{j}p+t$ for some $p\geqslant 1$. Hence, to complete the proof of the desired equivalence, it remains to check that if $m=2^{j}p+t$, then Eq. (16) holds. Now, if $x=0$, so that $m=2^{j}p$, Corollary 3 and Lemma  7 clearly imply Eq. (16) (cf. the case when t is even in the proof of Lemma 8). So, assume that $x>0$ and write it as $x=2^i(2y_0+1)$ with $0\leqslant i< j-2$ and $y_0<2^{j-i-3}$. Then

  $$\begin{aligned}&c_{m+2^j-t}+c_m+2^j-t\\&\quad =c_{2^{j}p+2x+2^j-2x}+c_{2^{j}p+2x}+2^j-2x\\&\quad = c_{2^{j}p+2^{i+1}(2y_0+1)+2^{j}-2^{i+1}(2y_0+1)}\\&\qquad +c_{2^{j}p+2^{i+1}(2y_0+1)}+2^{j}-2^{i+1}(2y_0+1)\\&\quad =2^{i+1}\big (c_{2^{j-i-1}p+2y_0+1+2^{j-i-1} -(2y_0+1)}\\&\qquad +c_{2^{j-i-1}p+2y_0+1}+2^{j-i-1}-(2y_0+1)\big )\\&\quad =2^{i+1} c_{2^{j-i}p+4y_0+2+2^{j-i-1}-(2y_0+1)}\quad \text{(by } \text{ the } \text{ induction } \text{ hypothesis) }\\&\quad =c_{2^{j+1}p+2^{j}+2^{i+1}(2y_0+1)}=c_{2^{j+1}p+2^{j}+2x}\\&\quad =c_{2m+2^j-t} \end{aligned}$$

  as we wanted to prove.

• If $t=2x+1$ for some $0\leqslant x<2^{j-2}$, Eq. (17) and Lemma  7 imply that $m+1$ is even, and then m is odd, say $m=2m_0+1$ for some $m_0\geqslant 0$, and Eq. (16) can be written

  $$\begin{aligned} c_{2m_0+1+2^j-2x-1}+c_{2m_0+1}+2^j-2x-1= c_{4m_0+2+2^j-2x-1}. \end{aligned}$$

  (18)

  Now, if $m_0=0$, Remark 2.(a) implies that this equality holds if, and only if, $2^j-2x-1=1$ which, under the condition $0\leqslant x<2^{j-2}$, only happens when $j=1$ and $x=0$, but then $t=1=2^{j-1}$ against the assumption that $t<2^{j-1}$. Therefore $m_0$ must be at least 1. Then, by induction, Identity (18) is equivalent to $m_0=2^{j-1}p+x$ for some $p\geqslant 1$, that is, to $m=2m_0+1=2^{j}p+2x+1=2^{j}p+t$ for some $p\geqslant 1$. So, to complete the proof of the desired equivalence, it remains to check that if $m=2^{j}p+t$, then Eq. (17) holds. Now, in the current situation:

  $$\begin{aligned}&c_{m+2^j-t}+c_{m+1}+2^j-t-1\\&\quad =c_{2^{j}p+2x+1+2^j-2x-1}+c_{2^{j}p+2x+2}+2^j-2x-2\\&\quad =c_{2^{j}p+2^j}+c_{2^{j}p+2x+2}+2^j-2x-2\\&\quad = 2\big (c_{2^{j-1}p +2^{j-1}}+c_{2^{j-1}p+x+1}+2^{j-1}-x-1\big )\\&\quad = 2\big (c_{(2^{j-1}p+x+1)+(2^{j-1}-x-1)}+c_{2^{j-1}p+x+1}+2^{j-1}-x-1\big )=(**) \end{aligned}$$

  If x is even, say $x=2x_0$ with $0\leqslant x_0<2^{j-3}$, then

  $$\begin{aligned} (**)&=2\big (c_{(2^{j-1}p+2x_0+1)+(2^{j-1}-2x_0-1)}+c_{2^{j-1}p+2x_0+1}+2^{j-1}-2x_0-1\big )\\&= 2c_{2^{j}p+2(2x_0+1)+2^{j-1}-(2x_0+1)} \quad \text{(by } \text{ the } \text{ induction } \text{ hypothesis) }\\&=c_{2^{j+1}p+2^{j}+4x_0+2} =c_{2m+2^j-t+1}. \end{aligned}$$

  And if x is odd, write it as $x=2^i(2t_0+1)-1$ with $1\leqslant i<j-1$ and $t_0<2^{j-i-3}$, and then

  $$\begin{aligned} (**)&=2\big (c_{2^{j-1}p+2^i(2t_0+1)+2^{j-1}-2^i(2t_0+1)}\\&\qquad +c_{2^{j-1}p+2^i(2t_0+1)}+2^{j-1}-2^i(2t_0+1)\big )\\&= 2^{i+1}\big (c_{2^{j-i-1}p+2t_0+1+2^{j-i-1}-(2t_0+1)}\\&\qquad +c_{2^{j-i-1}p+2t_0+1}+2^{j-i-1}-(2t_0+1)\big )\\&= 2^{i+1}c_{2^{j-i}p+4t_0+2+2^{j-i-1}-(2t_0+1)} \quad \text{(by } \text{ the } \text{ induction } \text{ hypothesis) }\\&= c_{2^{j+1}p+2^{i+1}(2t_0+1)+2^{j}}=c_{2^{j+1}p+2x+2+2^{j}}\\&=c_{2m+2^j-t+1} \end{aligned}$$

  This completes the proof of the desired equivalence when t is odd.

$\square$

We are now in a position to proceed with the proof of Proposition 2. Assertion (1) in it is a direct consequence of Corollary 3. So, assume $n_a>n_b$ and set $s=n_a-n_b$, so that $n_a=n_b+s$. Then:

• (a) If $s=1$, then, by Lemma 9, $c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b}$ for every $n_b\geqslant 1$.

• (b) If $s>1$ is odd, write it as $s=2^{j+1}-(2t+1)$, with $j={\lfloor }\log _2(s){\rfloor }\geqslant 1$ and $0\leqslant t<2^{j-1}$. Then, by Lemmas 8 and 9, $c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b}$ if, and only if, either $n_b=2^{j+1}p$ or $n_b=2^{j+1}p+2t+1$, for some $p\geqslant 1$.

• (c) If $s\geqslant 2$ is even, write it as $s=2^ks_0$, with $k\geqslant 1$ the largest exponent of a power of 2 that divides s and $s_0$ an odd integer, and write the latter as $s_0=2^{j+1}-(2t+1)$ with $j={\lfloor }\log _2(s_0){\rfloor }\geqslant 0$ and $0\leqslant t<2^{j-1}$. Then, by Lemma 7, $c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b}$ if, and only if, $n_b=2^km$, for some $m\geqslant 1$ such that $c_{m+s_0}+c_m+s_0=c_{2m+s_0},$ and then:

  • If $s_0=1$ (equivalently, if $j=0$), $c_{m+s_0}+c_m+s_0=c_{2m+s_0}$ for every $m\geqslant 1$ and therefore, in this case, $c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b}$ for every $n_b=2^km$ with $m\geqslant 1$.

  • If $s_0>1$ (equivalently, if $j>0$), Lemmas 8 and 9 imply that $c_{m+s_0}+c_m+s_0=c_{2m+s_0}$ if, and only if, $m=2^{j+1}p$ or $m=2^{j+1}p+2t+1$, for some $p\geqslant 1$. Therefore, in this case, $c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b}$ if, and only if, $n_b=2^{k+j+1}p$ or $n_b=2^k(2^{j+1}p+2t+1)$, for some $p\geqslant 1$.

Combining the three cases, and taking $k=0$ in the odd s case, we conclude that

$$\begin{aligned} c_{n_a}+c_{n_b}+n_a-n_b=c_{n_a+n_b} \end{aligned}$$

if, and only if, writing $n_a-n_b=2^k(2^{j+1}-(2t+1))$ (for some $k\geqslant 0$, $j\geqslant 0$, and $0\leqslant t<2^{j-1}$),

• If $j=0$, then $n_b=2^kp$ for some $p\geqslant 1$, in which case $n_a=2^k(p+1)$ and $n=2^{k}(2p+1)$.

• If $j>0$, then there exists some $p\geqslant 1$ for which one of the following conditions holds:

  • $n_b=2^{k+j+1}p$, in which case $n_a=2^k(2^{j+1}(p+1)-(2t+1))$ and $n=2^k(2^{j+1}(2p+1)-(2t+1))$.

  • $n_b=2^k(2^{j+1}p+2t+1)$, $n_a=2^{k+j+1}(p+1)$ and $n=2^k(2^{j+1}(2p+1)+ 2t+1)$.

This is equivalent to the expressions for $n_a$ and $n_b$ in option (2) in the statement (replacing $j+1$ with $j>0$ by $l\geqslant 2$).

This completes the proof of Proposition 2.

1.2 A.2 Proof of Proposition 5

This appendix is devoted to establish the following result.

Proposition 5

Let $T_n^{ gfb }=(T_a,T_b)$ be a GFB tree with $n\geqslant 2$, $T_a\in {\mathcal {T}}_{n_a}$, $T_b\in {\mathcal {T}}_{n_b}$ and $n_a\geqslant n_b$. Let $n=2^m+p$ with $m=\lfloor \log _2(n)\rfloor$ and $0\leqslant p<2^m$. Then, we have:

• (i) If $0\leqslant p\leqslant 2^{m-1}$, then $n_a = 2^{m-1}+p$, $n_b = 2^{m-1}$ and $T_b$ is fully symmetric.

• (ii) If $2^{m-1}\leqslant p<2^m$, $n_a = 2^{m}$, $n_b=p$ and $T_a$ is fully symmetric.

The proof of this proposition requires of the following lemma. The idea guiding its proof is illustrated in Fig. 9.

Lemma 10

Let $n\geqslant 3$ be an odd natural number. Then, $T_n^{ gfb }$ shares a maximal pending subtree with $T_{n-1}^{ gfb }$ and a maximal pending subtree with $T_{n+1}^{ gfb }$.

Proof

Since $n\geqslant 3$ is odd, the first $(n-1)/{2}$ iterations of the loop in Algorithm 2 result in ${(n-1)}/{2}$ cherries and a single node, which in the $(n+1)/{2}$-th iteration is clustered with a cherry to form a tree with 3 leaves. From this moment on, as the algorithm continues clustering trees, in each i-th iteration there will be one, and only one, tree $T_i^{odd}$ with an odd number s(i) of leaves. Note now that, on the one hand, this unique tree with s(i) leaves is treated by the algorithm like a tree with $s(i)-1$ leaves, except that it is clustered as late as possible, i.e. when all other trees in $treeset$ with $s(i)-1$ leaves (if there are any) have already been clustered. On the other hand, however, this tree is also treated by the algorithm like a tree with $s(i)+1$ leaves, except that it is clustered as early as possible, i.e. before any other elements in $treeset$ with $s(i)+1$ leaves (if there are any) get clustered. So, to summarize, after the first $i\geqslant (n+1)/{2}$ iterations of the loop, $treeset$ contains a unique tree $T_i^{odd}$ with an odd number s(i) of leaves, which at the same time

• (i) is treated like a tree with $s(i)-1$ leaves, but is clustered as late as possible;

• (ii) is treated like a tree with $s(i)+1$ leaves, but is clustered as soon as possible.

Fig. 9

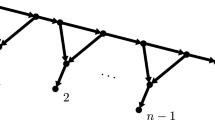
Content of $treeset$ before the $i^{\mathrm{th}}$ iteration of the loop in Algorithm 2 for $n=10, n=11$ and $n=12$. In case of $n=11$, the tree with white leaves for $i=7, \ldots , 10$, depicts the unique tree in $treeset$ with an odd number of leaves. For $n=10$, the leaf depicted as a diamond represents leaf u used in the proof of Lemma 10. Note that the tree containing this leaf is always clustered as late as possible. In case of $n=12$, the leaf depicted as a diamond again represents leaf u used in the proof of Lemma 10. In this case, the tree containing this leaf is always clustered as soon as possible. The last tree depicted in each column represents the GFB tree. Note that $T_n^{ gfb }$ can be obtained from $T_{n-1}^{ gfb }$ by replacing the leaf depicted as a diamond by a cherry. Moreover, $T_n^{ gfb }$ can be obtained from $T_{n+1}^{ gfb }$ by replacing the cherry containing the diamond leaf by a single leaf

Now, first consider Algorithm 2 for $n-1$, which is an even number. After the first $(n-3)/{2}$ iterations of the loop, $treeset$ contains $(n-3)/{2}$ trees with 2 leaves and two trees with 1 leaf, which are clustered last to form the last cherry. We keep tracking one leaf u of this cherry throughout the algorithm. The algorithm at this stage contains only cherries, which are all isomorphic, so without loss of generality, we may assume that u is contained in the one that gets clustered with another tree last, i.e. after all other cherries have been clustered. We continue like this, always assuming without loss of generality (when there is more than one tree in $treeset$ of the same size as the tree that contains u) that the tree containing u is in the last one to be clustered. By (i), this means that if we replace u in $T_{n-1}^{ gfb }$ by a cherry, we derive $T_{n}^{ gfb }$. This is due to the fact that in the analogous step where $treeset$ for $n-1$ only contains cherries, $treeset$ for n will contain only cherries and a tree containing three leaves. This triplet will subsequently act like a cherry, but like the one that happens to be clustered last. So, we identify the cherry in this triplet with u to see the correspondence between $T_{n-1}^{ gfb }$ and $T_{n}^{ gfb }$. Note that this directly implies that $T_{n-1}^{ gfb }$ and $T_{n}^{ gfb }$ share a common maximal pending subtree—namely the one that does not contain u.

Note that by (ii), an analogous procedure for $n+1$ leads to $T_{n+1}^{ gfb }$ and $T_{n}^{ gfb }$ sharing a common maximal pending subtree. In this case, we track a cherry in $T_{n+1}^{ gfb }$, namely the one that happens to be clustered first, and replace it by a single leaf to see the correspondence between $T_{n+1}^{ gfb }$ and $T_{n}^{ gfb }$. This completes the proof. $\square$

We can proceed now to prove Proposition 5. Let $n=2^m+p$ with $m=\lfloor \log _2(n)\rfloor$ and $0\leqslant p<2^m$. We shall prove by induction on n that if $T_n^{ gfb }=(T_a,T_b)$ is a GFB tree with $n\geqslant 2$, $T_a\in {\mathcal {T}}_{n_a}$, $T_b\in {\mathcal {T}}_{n_b}$ and $n_a\geqslant n_b$ then:

• (i) If $0\leqslant p\leqslant 2^{m-1}$, $n_a = 2^{m-1}+p$ and $n_b = 2^{m-1}$ and then $T_b$ is fully symmetric.

• (ii) If $2^{m-1}\leqslant p<2^m$, we have $n_a = 2^{m}$ and $n_b=p$ and then $T_a$ is fully symmetric.

We want to point out that we understand that the conjunction of these two assertions in the case when both premises are satisfied, namely when $p=2^{m-1}$, says that $n_a =2^m$ and $n_b = 2^{m-1}$ and then both $T_a$ (by (ii)) and $T_b$ (by (i)) are fully symmetric.

The base case for (i) is when $n=2$ and for (ii), when $n=3$. In both cases the assertions are obvious, because there is only one bifurcating tree with $2=2^1+0$ leaves (a cherry with $n_a=n_b=1=2^{0}$) and only one bifurcating tree with $3=2^1+1$ leaves (a caterpillar with $n_a=2=2^1$ and $n_b=1$).

Now, let $n \geqslant 4$ and assume that (i) and (ii) hold for up to $n-1$ leaves. Let $T=(T_a,T_b)$ be a GFB tree with n leaves, with $T_a\in {\mathcal {T}}_{n_a}$, $T_b\in {\mathcal {T}}_{n_b}$ and $n_a\geqslant n_b$ Recall that $T_a$ and $T_b$ are again GFB trees by Lemma 5. We distinguish two cases, depending on the parity of n:

• Assume that n is even, say $n=2n_0$ with $n_0\geqslant 2$. In this case, Algorithm 2 results in a tree $T^{ gfb }_n$ with $n_0$ cherries (because in each of the first $n_0$ iterations of the loop a pair of nodes are merged into a cherry). We now consider the tree $T'$ with $n_0$ leaves that is obtained from $T^{ gfb }_n$ by replacing all cherries by single leaves. Let $T'=(T_a',T_b')$ be the decomposition into maximal pending subtrees, with $T_a'\in {\mathcal {T}}_{n_a'}$, $T_b'\in {\mathcal {T}}_{n_b'}$ and $n_a'\geqslant n_b'$. By construction, $T_a$ and $T_b$ are obtained by replacing the leaves of $T_a'$ and $T_b'$ by cherries, and therefore, in particular, $n_a=2n_a'$ and $n_b=2n_b'$. Note now that, since $T^{ gfb }_n$ is a GFB tree, so is $T'$ (because as soon as Algorithm 2 only has cherries to choose from, they are treated like leaves). Note also that, since n is even, so is p, say $p=2p_0$, and $n_0=2^{m-1}+p_0$. Then we have that:

  • (i) If $0\leqslant p\leqslant 2^{m-1}$, then $0\leqslant p_0\leqslant 2^{m-1-1}$ and hence, by the induction hypothesis, $n_a'=2^{m-2}+p_0$, $n_b'=2^{m-2}$, and $T_b'$ is fully symmetric, which implies that $n_a=2n_a'=2^{m-1}+2p_0=2^{m-1}+p$, $n_b=2n_b'=2^{m-1}$, and $T_b$ is fully symmetric, because it is obtained from the fully symmetric tree $T_b'$ by replacing all its leaves by cherries.

  • (ii) If $2^{m-1}\leqslant p< 2^{m}$, then $2^{m-1-1}\leqslant p_0\leqslant 2^{m-1}$ and hence, by the induction hypothesis, $n_a'=2^{m-1}$, $n_b'=p_0$, and $T_a'$ is fully symmetric, which implies that $n_a=2n_a'=2^{m}$, $n_b=2n_b'=2p_0=p$, and, arguing as in (i), $T_a$ is fully symmetric.

• Assume that n is odd, say $n=2n_0+1$ with $n_0\geqslant 2$. In this case both $n-1=2n_0$ and $n+1=2(n_0+1)$ are even. Write $n=2^m+p$ and $p=2p_0+1$, so that $n_0=2^{m-1}+p_0$ with $0\leqslant p_0<2^{m-1}$. Let $T^1 :=T_{n-1}^{ gfb }$ and $T^2:=T_{n+1}^{ gfb }$. The tree $T^1$ satisfies (i) and (ii) by the induction hypothesis, and it can be proved that $T^2$ also satisfies these assertions by arguing as in the previous case when n is even (i.e. replacing the pending $n_0+1$ cherries in $T^2$ by single leaves, noticing that the resulting tree is GFB, applying the induction hypothesis to it and finally returning back to $T^2$ by replacing leaves by cherries). Let $T^1=(T^1_a, T^1_b)$—with $T^1_a\in {\mathcal {T}}_{n^1_a}$ and $T^1_b\in {\mathcal {T}}_{n^1_b}$ and $n^1_a\geqslant n^1_b$—and $T^2=(T^2_a, T^2_b)$—with $T^2_a\in {\mathcal {T}}_{n^2_a}$ and $T^2_b\in {\mathcal {T}}_{n^2_b}$ and $n^2_a\geqslant n^2_b$—denote the decompositions of $T^1$ and $T^2$ into maximal pending subtrees, respectively. Note that, since n is odd, $p\ne 0,2^{m-1}$. Now we have:

  • (i) If $0< p<2^{m-1}$, then $n-1=2^m+(p-1)$ with $0\leqslant p-1<2^{m-1}$ and $n+1=2^m+(p+1)$ with $0<p+1\leqslant 2^{m-1}$. Then, since $T^1$ and $T^2$ satisfy assertion (i),

    $$\begin{aligned} n^1_a=2^{m-1}+p-1,\ n^1_b=2^{m-1},\ n^2_a=2^{m-1}+p+1,\ n^2_b=2^{m-1} \end{aligned}$$

    and both $T_b^1$ and $T_b^2$ are fully symmetric and hence (since they have the same numbers of leaves) $T_b^1=T_b^2$. Now, we know by Lemma 10 that T shares a maximal pending subtree with $T^1$ and a maximal pending subtree with $T^2$. Looking at the numbers of leaves of the maximal pending subtrees of $T^1$ and $T^2$, one easily deduces that the only possibility for this to happen is that T shares with $T^1$ and $T^2$ the same maximal pending subtree: the fully symmetric subtree $T_b^1=T_b^2$. (Indeed, since $T_a^1\ne T_a^2$, because they have different numbers of leaves, if T did not share $T_b^1=T_b^2$ with both $T^1$ and $T^2$, then it would have a maximal pending subtree in common with $T^1$ and the other maximal pending subtree in common with $T^2$, but no combination of a maximal pending subtree of $T^1$ and a maximal pending subtree of $T^2$ yields a tree with $2^m+p$ leaves.) A fortiori, one of the maximal pending subtrees of T is a fully symmetric tree with $2^{m-1}$ leaves and the other must have, thus, the remaining $2^{m-1}+p$ leaves. This shows that $n_a=2^{m-1}+p$ and $n_b=2^{m-1}$ and $T_b$ is fully symmetric.

  • (ii) If $2^{m-1}<p\leqslant 2^{m}-3$ then $n-1=2^m+(p-1)$ with $2^{m-1}\leqslant p-1<2^{m}$ and $n+1=2^m+(p+1)$ with $2^{m-1}<p+1< 2^{m}$. Then, since $T^1$ and $T^2$ satisfy assertion (ii),

    $$\begin{aligned} n^1_a=2^{m},\ n^1_b=p-1,\ n^2_a=2^{m},\ n^2_b=p+1 \end{aligned}$$

    and both $T_a^1$ and $T_a^2$ are fully symmetric and hence (since they have the same numbers of leaves) $T_a^1=T_a^2$. Reasoning as in the previous case, we deduce that T shares with both $T^1$ and $T^2$ the fully symmetric maximal pending subtree $T_a^1=T_a^2$. In particular, one of its maximal pending subtrees has $2^{m}$ leaves (and it is fully symmetric) and the other must have, thus, the remaining p leaves. This shows that $n_a=2^{m}$ and $n_b=p$ and $T_a$ is fully symmetric.

  • (iii) Consider finally the case when $p= 2^{m}-1> 2^{m-1}$. Then, $n-1=2^m+(p-1)$ with $2^{m-1}\leqslant p-1<2^{m}$ and $n+1=2^{m+1}$. In this case, since $T^1$ satisfies assertion (ii) and $T^2$ satisfies assertion (i),

    $$\begin{aligned} n^1_a=2^{m},\ n^1_b=2^{m}-2,\ n^2_a=2^{m},\ n^2_b=2^{m} \end{aligned}$$

    and $T_a^1$, $T_a^2$ and $T_b^2$ are fully symmetric and hence (since they have the same numbers of leaves) $T_a^1=T_a^2=T_b^2$. Arguing as in the previous cases we conclude that T has a maximal pending subtree with $2^m$ leaves that is fully symmetric and the other maximal pending subtree with the remaining $2^m-1$ leaves, and hence it satisfies assertion (ii).

This completes the proof.

1.3 A.3 Proof of Proposition 8

This appendix is devoted to establish the following result.

Proposition 8

For every $n\geqslant 1$, let $n=\sum _{i=1}^\ell 2^{m_i}$, with $\ell \geqslant 1$ and $m_1>\cdots > m_\ell$, be its binary expansion.

• (a) $s(T_n^ gfb )=n-1-(m_1-m_\ell )$.

• (b) For every $T\in \widetilde{\mathcal {MC}}_n$, if $T\ne T_n^ gfb$, then $s(T)< s(T_n^ gfb )$.

Proof

Note first of all that the number s of symmetry vertices satisfies the following recurrence: if $T\in {\mathcal {T}}_1$, then $s(T)=0$, and if $T=(T_a,T_b)\in {\mathcal {T}}_n$ with $n\geqslant 2$, then

$$\begin{aligned} s(T) = {\left\{ \begin{array}{ll} s(T_a) + s(T_b) + 1, &{}\text { if }T_a\text { and }T_b\text { are isomorphic},\\ s(T_a)+ s(T_b) &{}\text { otherwise}. \end{array}\right. } \end{aligned}$$

(19)

We shall now prove (a) by induction on n. When $n=1=2^0$, the statement holds because $s(T_1^ gfb )=0 = 1-1-(0-0) = n-1-(m_1-m_\ell )$. More in general, the statement clearly holds whenever n is a power of 2, say $n=2^{m_1}$, because in this case $T^{ gfb }_n$ is fully symmetric and therefore all its internal nodes are symmetry vertices, i.e. $s(T^{ gfb }_n)=n-1=n-1-(m_1-m_1)$.

Now assume that the statement holds for every GFB tree with $n'$ leaves, with $n'<n$, and consider the tree $T^{ gfb }_n$. By Lemma 5, if $T^{ gfb }_n= (T_a, T_b)$, then $T_a$ and $T_b$ are GFB trees and, by the inductive hypothesis, the statement holds for $T_a=T_{n_a^ gfb }^ gfb$ and $T_b=T_{n_b^ gfb }^ gfb$.

Let us now write n as $2^m+p$ with $m = \lfloor \log _2(n) \rfloor$ and $0 \leqslant p < 2^m$, and consider its binary expansion $n = \sum _{j=1}^\ell 2^{m_j}$ with $m_1>\cdots >m_\ell$, so that $m_1=m$ and $p = \sum _{j=2}^\ell 2^{m_j}$ is the binary expansion of p if $p>0$. Now, we distinguish four cases:

• (i) If $p=0$, then n is a power of 2, in which case we have already seen that the statement holds.

• (ii) If $1\leqslant p<2^{m-1}$, then, by Proposition 5, $n_a^ gfb = 2^{m-1} + p$ and $n_b^ gfb = 2^{m-1}$ and $T_b$ is fully symmetric. In this case, $m_2<m-1=m_1-1$ and thus $n_a^ gfb = 2^{m_1 - 1} + \sum _{j=2}^\ell 2^{m_j}$ is the binary expansion of $n_a^ gfb$. Then $s(T_b)=2^{m-1}-1$ and, by the induction hypothesis,

  $$\begin{aligned} s(T_a)=2^{m-1} + p-1-(m_1-1-m_\ell )=2^{m-1} + p-(m_1-m_\ell ) \end{aligned}$$

  and hence

  $$\begin{aligned} s(T^{ gfb }_n)= & {} s(T_a) + s(T_b)= 2^{m-1} + p-(m_1-m_\ell ) + 2^{m-1}-1\\= & {} n- 1- (m_1 - m_\ell ). \end{aligned}$$

• (iii) If $p= 2^{m-1}$, so that $n=2^m+2^{m-1}$ is the binary expansion of n, then, by Proposition 5, $n_a^ gfb = 2^{m}$ and $n_b^ gfb =2^{m-1}$ and both $T_a$ and $T_b$ are fully symmetric. In this case, $s(T_a)=2^m-1$ and $s(T_b)=2^{m-1}-1$ and hence

  $$\begin{aligned} s(T^{ gfb }_n)&= s(T_a) + s(T_b)= 2^m-1 + 2^{m-1}-1 \\&= 2^m + 2^{m-1} - 1 - (m-(m-1)) = n-1-(m_1-m_\ell ). \end{aligned}$$

• (iv) Finally, assume that $p > 2^{m-1}$, so that its binary expansion is $p= 2^{m-1} + \sum _{i=3}^\ell 2^{m_i}$, and in particular $m_2=m-1=m_1-1$. In this case, by Proposition 5, $n_a^ gfb = 2^m$, and $T_a$ is fully symmetric, and $n_b^ gfb = p$. Then, $s(T_a)=2^m-1$ and, by the induction hypothesis, $s(T_b)=p-1-(m_1-1-m_\ell )=p-(m_1-m_\ell )$ and hence

  $$\begin{aligned} s(T) = s(T_a) + s(T_b) = 2^{m}-1+p-(m_1-m_\ell )= n-1-(m_1 - m_\ell ). \end{aligned}$$

This completes the proof of (a).

As far as (b) goes, we also prove it by induction on n. The case $n=1$ is obvious, since there is only one bifurcating tree in ${\mathcal {T}}_1$. Let now $n\geqslant 2$ and assume that the statement is true for every number $n'$ of leaves smaller than n. Let $T = (T_a,T_b)$, with $T_a\in {\mathcal {T}}_{n_a}$, $T_b\in {\mathcal {T}}_{n_b}$, and $n_a\geqslant n_b$, be a minimal Colless tree with n leaves such that s(T) is maximum in $\widetilde{\mathcal {MC}}_n$. We want to prove that $T=T^{ gfb }_n$.

By Lemma 2, $T_a\in \widetilde{\mathcal {MC}}_{n_a}$ and $T_b\in \widetilde{\mathcal {MC}}_{n_b}$ and therefore, by the inductive hypothesis, $s(T_a)\leqslant s(T_{n_a}^ gfb )$ and $s(T_b)\leqslant s(T_{n_b}^ gfb )$. To prove that $T=T^{ gfb }_n=(T_{n_a^ gfb }^ gfb ,T_{n_b^ gfb }^ gfb )$, it is enough to prove that $n_a=n_a^ gfb$ and $n_b=n_b^ gfb$ (and, actually, it is enough to prove one of these equalities, because then the other will follow from $n_a+n_b=n=n_a^ gfb +n_b^ gfb$) and that $s(T_a)= s(T_{n_a}^ gfb )$ and $s(T_b)= s(T_{n_b}^ gfb )$ (because by the inductive hypothesis these equalities imply that $T_a=T_{n_a}^ gfb$ and $T_b=T_{n_b}^ gfb$). Let $n_a=\sum _{i=1}^{\ell _a} 2^{s_i}$ and $n_b=\sum _{i=1}^{\ell _b} 2^{t_i}$ be the binary decompositions of $n_a$ and $n_b$.

Now, two cases arise, depending on whether the root of T is a symmetry vertex or not. Let us assume first that it is a symmetry vertex, i.e, that $T_a=T_b$. In this case, n must be even and $n_a = n_b = n/2=\sum _{i=1}^{\ell } 2^{m_i-1}$. In particular $s_1=t_1=m_1-1$ and $s_{\ell _a}=t_{\ell _b}=m_{\ell }-1$. Moreover, it must happen that $s(T_a)= s(T_{n/2}^ gfb )$, because if $s(T_a)< s(T_{n/2}^ gfb )$ and if we denote by $T'$ the tree $(T_{n/2}^ gfb ,T_{n/2}^ gfb )$, then $T'\in \widetilde{\mathcal {MC}}_n$ by Proposition 1 (recall that (n/2, n/2) always belongs to QB(n)) and, by Eq. (19),

$$\begin{aligned} s(T)=2s(T_a)+1<2s(T_{n/2}^ gfb )+1=s(T') \end{aligned}$$

against the assumption that s(T) is maximum in $\widetilde{\mathcal {MC}}_n$. So, in this case it remains to prove that $n_a^ gfb =n_b^ gfb =n/2$.

Now, applying Eq. (19) and (a), we have that

$$\begin{aligned} s(T)&=2s(T_a) + 1 =2s(T_{n/2}^ gfb ) + 1 = 2\Big (\frac{n}{2}-1-(s_1-s_{\ell _a})\Big )+1\\&= n-1-2(m_1-1-m_\ell +1)=n-1-2(m_1-m_\ell )\\&=s(T_{n}^ gfb )-(m_1-m_\ell ). \end{aligned}$$

Thus, if $\ell >1$, then $s(T)<s(T_n^ gfb )$, against the assumption that s(T) is maximum in $\widetilde{\mathcal {MC}}_n$. Therefore, $\ell =1$, i.e. $n=2^{m_1}$ and hence $n_a^ gfb =n_b^ gfb =n/2=n_a=n_b$, as we wanted to prove.

Let us assume now that the root of T is not a symmetry vertex. Recall from Corollary 9 that

$$\begin{aligned} n_b^ gfb \leqslant n_b\leqslant n_a\leqslant n_a^ gfb . \end{aligned}$$

Combining these inequalities with Proposition 5 we obtain that:

• If $0\leqslant p< 2^{m_1-1}$, then

  $$\begin{aligned} 2^{m_1-1}=n_b^ gfb \leqslant n_b\leqslant n_a\leqslant n_a^ gfb = 2^{m_1-1}+p<2^{m_1}, \end{aligned}$$

  (20)

  and then, in this case, $s_1=t_1=m_1-1$.

• If $2^{m_1-1}\leqslant p<2^{m_1}$, then

  $$\begin{aligned} 2^{m_1-1}\leqslant p =n_b^ gfb \leqslant n_b\leqslant n_a\leqslant n_a^ gfb =2^{m_1} \end{aligned}$$

  (21)

  and then either $n_a=2^{m_1}=n_a^ gfb$, in which case $n_b=p=n_b^ gfb <2^{m_1}$, $s_1=m_1$, and $t_1=m_1-1$, or $2^{m_1-1}\leqslant n_b\leqslant n_a<n_a^ gfb =2^{m_1}$, in which case $s_1=t_1=m_1-1$.

So, in particular, $t_1$ is always $m_1-1$, and $s_1$ is $m_1$, when $n_a=2^{m_1}=n_a^ gfb$, and $m_1-1$ otherwise. Moreover, since $n_a+n_b=n$, it always happens that $\min \{s_{\ell _a}, t_{\ell _b}\} \leqslant m_\ell$.

Now, in this case we have again that $s(T_a)=s(T_{n_a}^ gfb )$ and $s(T_b)=s(T_{n_b}^ gfb )$, because if, say, $s(T_a)<s(T_{n_a}^ gfb )$ and if we replace in T its maximal pending subtree $T_a$ by $T_{n_a}^ gfb$, then, by Proposition 1 (and recalling that, since $T\in \widetilde{\mathcal {MC}}_n$, by that very proposition we have that $(n_a,n_b)\in QB(n)$), the resulting tree $T'=(T_{n_a}^ gfb ,T_b)$ is still minimal Colless and, by Eq. (19),

$$\begin{aligned} s(T) =s(T_a)+s(T_b)<s(T_{n_a}^ gfb )+s(T_b)\leqslant s(T') \end{aligned}$$

against the assumption that s(T) is maximum in $\widetilde{\mathcal {MC}}_n$. So, $T_a=T_{n_a}^ gfb$ and $T_b=T_{n_b}^ gfb$. It remains to prove that $n_a=n_a^ gfb$ and $n_b=n_b^ gfb$.

By Eq. (19) and (a), we have that

$$\begin{aligned} s(T)&=s(T_a) + s(T_b) =s(T_{n_a}^ gfb ) + s(T_{n_b}^ gfb )\nonumber \\&= n_a-1-(s_1-s_{\ell _a})+n_b-1-(t_1-t_{\ell _b})\nonumber \\&= n-2-(s_1-s_{\ell _a})-(m_1-1-t_{\ell _b})\nonumber \\&= n-1-(m_1-m_\ell )-(s_1+m_\ell -s_{\ell _a}-t_{\ell _b})\nonumber \\&=s(T_{n}^ gfb )-(s_1+m_\ell -s_{\ell _a}-t_{\ell _b}) \end{aligned}$$

(22)

We consider now several possibilities:

• If $s_{\ell _a}=s_1$, then $n_a=2^{s_1}$, where $s_1$ is $m_1-1$ or $m_1$. Now, since $2^{m_1-1}\leqslant n_b\leqslant n_a$ and $n_a+n_b=2^{m_1}+p$, if we had $n_a=2^{m_1-1}$, we would also have $n_b=2^{m_1-1}$ and $p=0$, and then $n_a^ gfb =n_a=n_b=n_b^ gfb$; but then $T_a=T_{n_a}^ gfb$ and $T_b=T_{n_b}^ gfb$ would be isomorphic to the fully symmetric tree $T_{m_1-1}^ fs$ and hence the root of T would be a symmetry vertex, against the current assumption that it is not so.

  So, in this case we have $n_a=2^{m_1}$. By properties (20) and (21), it can only happen when $2^{m_1-1}\leqslant p$ and $n_a= n_a^ gfb$, and then $n_b= n_b^ gfb$, too.

• If $s_{\ell _a}<s_1$ and $t_{\ell _b}\leqslant s_{\ell _a}$, then $t_{\ell _b}=\min \{s_{\ell _a}, t_{\ell _b}\} \leqslant m_\ell$ and hence, by (22),

  $$\begin{aligned} s(T)=s(T_{n}^ gfb )-(s_1+m_\ell -s_{\ell _a}-t_{\ell _b})<s(T_{n}^ gfb ), \end{aligned}$$

  against the assumption that s(T) is maximum among all minimal Colless trees with n leaves.

• If $s_{\ell _a}<s_1$ and $s_{\ell _a}<t_{\ell _b}$, then $s_{\ell _a}=\min \{s_{\ell _a}, t_{\ell _b}\} \leqslant m_\ell$. Since in this case $n_a$ is not a power of 2, we have $s_1=t_1=m_1-1$ and then

  $$\begin{aligned} s_1+m_\ell -s_{\ell _a}-t_{\ell _b}\geqslant m_1-1-t_{\ell _b}=t_1-t_{\ell _b}\geqslant 0. \end{aligned}$$

  If one of these inequalities is strict, we deduce again that

  $$\begin{aligned} s(T)=s(T_{n}^ gfb )-(s_1+m_\ell -s_{\ell _a}-t_{\ell _b})<s(T_{n}^ gfb ), \end{aligned}$$

  reaching the same contradiction as before. Therefore, both inequalities are equalities and hence $s_{\ell _a}=m_\ell$ and $t_{\ell _b}=t_1=m_1-1$, which implies in particular that $n_b=2^{m_1-1}$. By (20) and (21), this can only happen when $0\leqslant p\leqslant 2^{m_1-1}$ and $n_b=2^{m_1-1}=n_b^ gfb$.

This finishes the proof of (b). $\square$

1.4 A.4 Computation of some probabilities under the $\beta$-model

Aldous’ $\beta$ model (Aldous 1996) is a probabilistic model of bifurcating phylogenetic trees that depends on one parameter $\beta \in (-2,\infty )$. As any other such probabilistic model, it yields a probabilistic model of bifurcating unlabeled trees, by defining the probability $P_\beta (T)$ of a tree $T\in {\mathcal {T}}_n$ as the sum of the probabilities of all phylogenetic trees on n leaves with shape T. This probabilistic model of bifurcating unlabeled trees satisfies the following Markovian recurrence. For every $m\geqslant 2$ and $k=1,\ldots ,m-1$, let

$$\begin{aligned} q_{m,\beta }(k)=\frac{1}{a_m(\beta )}\cdot \frac{\varGamma (\beta +k+1)\varGamma (\beta +m-k+1)}{\varGamma (k+1)\varGamma (m-k+1)}, \end{aligned}$$

where $a_m(\beta )$ is a suitable normalizing constant so that $\sum \limits _{a=1}^{m-1} q_{m,\beta }(a)=1$, and

$$\begin{aligned} {\widehat{q}}_{m,\beta }(k)=\left\{ \begin{array}{ll} q_{m,\beta }(k)+q_{m,\beta }(m-k)=2q_{m,\beta }(k) &{} \hbox { if}\ k\ne m/2\\ q_{m,\beta }(k) &{} \hbox { if}\ k= m/2 \end{array}\right. \end{aligned}$$

Then, if $T=(T_{a},T_b)\in {\mathcal {T}}_n$ with $T_a\in {\mathcal {T}}_{n_a}$, $T_b\in {\mathcal {T}}_{n_b}$ and $n_a\geqslant n_b$,

$$\begin{aligned} P_\beta (T)={\widehat{q}}_{n,\beta }(n_a)\cdot P_\beta (T_a)P_\beta (T_b). \end{aligned}$$

(23)

Recall that the Gamma function $\varGamma$ satisfies the recurrence $\varGamma (x+1)=x\varGamma (x)$ and that, for every $n\in {\mathbb {N}}_{\geqslant 1}$, $\varGamma (n)=(n-1)!$.

We want to compute the probabilities under this model of $T_6^ mb$ and $T_6^ gfb$. To do that, we shall need to compute all values $q_{6,\beta }(k)$ (we need all of them in order to compute the normalizing constant $a_6(\beta )$):

$$\begin{aligned} q_{6,\beta }(1)&=q_{6,\beta }(5)=\frac{1}{a_6(\beta )}\cdot \frac{\varGamma (\beta +2)\varGamma (\beta +6)}{\varGamma (2)\varGamma (6)}\\&= \frac{1}{a_6(\beta )}\cdot \frac{(\beta +5)(\beta +4)(\beta +3)(\beta +2)\varGamma (\beta +2)^2}{5!}\\ q_{6,\beta }(2)&=q_{6,\beta }(4)=\frac{1}{a_6(\beta )}\cdot \frac{\varGamma (\beta +3)\varGamma (\beta +5)}{\varGamma (3)\varGamma (5)}\\&= \frac{1}{a_6(\beta )}\cdot \frac{(\beta +4)(\beta +3)(\beta +2)^2\varGamma (\beta +2)^2}{2\cdot 4!}\\ q_{6,\beta }(3)&=\frac{1}{a_6(\beta )}\cdot \frac{\varGamma (\beta +4)^2}{\varGamma (4)^2}\\&= \frac{1}{a_6(\beta )}\cdot \frac{(\beta +3)^2(\beta +2)^2\varGamma (\beta +2)^2}{3!^2} \end{aligned}$$

Imposing now $\sum _{k=1}^5 q_{6,\beta }(k)=1$, i.e.

$$\begin{aligned} 1&=\frac{(\beta +3)(\beta +2)\varGamma (\beta +2)^2}{a_6(\beta )}\\&\qquad \cdot \Big (\frac{2(\beta +5)(\beta +4)}{5!}+\frac{2(\beta +4)(\beta +2)}{2\cdot 4!}+\frac{(\beta +3)(\beta +2)}{3!^2}\Big )\\&=\frac{(\beta +3)(\beta +2)\varGamma (\beta +2)^2(31 \beta ^2 + 194\beta + 300)}{a_6(\beta )\cdot 3\cdot 5!} \end{aligned}$$

and solving for $a_6(\beta )$, we obtain

$$\begin{aligned} a_6(\beta )=\frac{(\beta +3)(\beta +2)\varGamma (\beta +2)^2(31 \beta ^2 + 194\beta + 300)}{3\cdot 5!}. \end{aligned}$$

We can compute now the desired probabilities:

• As far as $P_\beta (T_6^ mb )$ goes, by Eq. (23) we have that

  $$\begin{aligned} P_\beta (T_6^ mb )=q_{6,\beta }(3)\cdot P_\beta (T_3^ mb )^2=q_{6,\beta }(3) \end{aligned}$$

  because ${\mathcal {T}}_3=\{T_3^ mb \}$ and hence $P_\beta (T_3^ mb )=1$. So,

  $$\begin{aligned} P_\beta (T_6^ mb )&= \frac{3\cdot 5!\cdot (\beta +3)^2(\beta +2)^2\varGamma (\beta +2)^2}{3!^2(\beta +3)(\beta +2)\varGamma (\beta +2)^2(31 \beta ^2 + 194\beta + 300)}\\&= \frac{10 (\beta +3)(\beta +2)}{31 \beta ^2 + 194\beta + 300}. \end{aligned}$$

• As to $P_\beta (T_6^ gfb )$ goes, by Eq. (23) (and the fact that $T_6^ gfb = (T_4^ gfb , T_2^ gfb )$ by Lemma 5 and Proposition 5) we have that

  $$\begin{aligned} P_\beta (T_6^ gfb )=2q_{6,\beta }(4)\cdot P_\beta (T_2^ gfb )P_\beta (T_4^ gfb ) \end{aligned}$$

  where $P_\beta (T_2^ gfb )=1$, because $T_2^ gfb$ is the only tree in ${\mathcal {T}}_2$;

  $$\begin{aligned} P_\beta (T_4^ gfb )= P_\beta (T_4^ mb )=\frac{3(\beta +2)}{7\beta +18} \end{aligned}$$

  by Lemma 4 in (Coronado et al. 2019); and

  $$\begin{aligned} q_{6,\beta }(4)&= \frac{3\cdot 5!\cdot (\beta +4)(\beta +3)(\beta +2)^2\varGamma (\beta +2)^2}{2\cdot 4!\cdot (\beta +3)(\beta +2)\varGamma (\beta +2)^2(31 \beta ^2 + 194\beta + 300)}\\&= \frac{15 (\beta +4)(\beta +2)}{2(31 \beta ^2 + 194\beta + 300)}. \end{aligned}$$

  So, finally,

  $$\begin{aligned} P_\beta (T_6^ gfb )&=2\cdot \frac{15 (\beta +4)(\beta +2)}{2(31 \beta ^2 + 194\beta + 300)}\cdot \frac{3(\beta +2)}{7\beta +18}\\&= \frac{45 (\beta +4)(\beta +2)^2}{(31 \beta ^2 + 194\beta + 300)(7\beta +18)}. \end{aligned}$$