Phase relationships between large and small scales in the turbulent boundary layer

Abstract

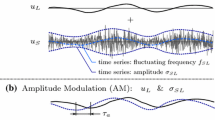
The apparent amplitude modulation effect between large- and small-scale motions in the turbulent boundary layer, including both streamwise and wall-normal velocity components, is explored by cross-correlation techniques. Single-point hotwire and planar PIV measurements are employed to consider the envelopes of small-scale fluctuations in both directions and their correlation with the fluctuations of large-scale motions in the streamwise direction. The degree of correlation is interpreted as a measure of phase lag between the different scale motions, and these phase measurements are used to demonstrate that the fluctuations in the envelope of small-scale motions in both directions tend to lead corresponding fluctuations in the large scales in the streamwise direction. The cospectral density of the cross-correlation between the different scales is used to identify the particular large-scale motions dominant in the modulation effect, and it is shown that the dominant interacting (or ‘modulating’) scale corresponds in size to the very large-scale motions observed in internal flows but not normally observed in the outer region of the boundary layer.

Appendices

Subfundamental sampling in PIV spatial cross-correlation

When the cross-correlation of two pure sinusoids is calculated, the result is a symmetric function if the sinusoids are perfectly in phase, and an antisymmetric function if the two sinusoids are out of phase by π/2. But this rule holds only when the signals are adequately resolved; when less than a full period of the signals is available, the symmetry/antisymmetry rules are broken significantly. In particular, for the case of a phase difference between velocity signals of π/2, the breaking of the antisymmetry of the cross-correlation functions means that the wall-normal location at which this phase difference is measured will no longer correspond to the zero-crossing of the correlation coefficient. The precise form of the discrepancy can be shown by considering two idealized signals separated by precisely that phase difference, $\cos{(x)}$ and $\cos{(x + \pi/2)}$, and calculating explicitly the cross-correlation as a function of the sample domain, [0,X]. For X = n π, n ≥ 2, the cross-correlation function is antisymmetric and identifies the phase lag accurately. However, for real (not necessarily integral) values of n <2, the cross-correlation function loses its antisymmetry: The (negative) trough moves closer to zero, thus causing the value of the correlation coefficient to be negative (and not zero) at the location of the π/2 phase lag between the signals, as shown in Fig. 9. As described above, the overall effect of this subfundamental sampling in real boundary layer signals is to cause the peak-to-trough switch to appear artificially further from the wall and distinctly higher than the zero-crossing of the correlation coefficient. The subfundamental sampling bias is also affected by the size of the filter and the amplitude of the small-scale fluctuations. The above, idealized model can then be elaborated to represent a velocity signal as a large scale superposed with a single small scale being modulated by the large scale, and thus the filtering effect in addition to the sampling period can be considered numerically. Such an analysis reveals that because the small-scale fluctuations in the wall-normal component have lower amplitude than the streamwise fluctuations, as seen in Hutchins and Marusic (2007), the subfundamental sampling effect is made significantly worse, and thus requires more extreme corrections with the filtering cutoff, as described above.

Fig. 9

The cross-correlation function using two idealized sinusoids to represent the large- and small-scale motions, with the wavelength of the large scale ten times that of the small scale and the amplitude one hundred times that of the small scale. On the left, the cross-correlation when a full period of the largest scale is captured; on the right, the cross-correlation when only a fraction of the period is sampled. The fraction is selected by assuming a dominant large scale of 6 δ and using the actual streamwise dimension of the PIV window

Robust fit of cospectral density ridgeline

In order to fit the ridgeline of the cospectral density map, which represents the dominant interacting scale between the large scales and the envelope of small-scale fluctuations, a simple power law relationship was assumed, in Eq. (5). By reversing Taylor’s hypothesis via the mean velocity profile, Eq. (6), the peak frequency in the cospectral density map can also be written as a power law, in Eq. (7). The power law mean velocity profile fit follows from the standard 1/7 power law form for turbulent boundary layers, with Reynolds number naively included for compatibility with the overall scaling in Eq. (5).

$$ \lambda_x/\delta = 10^a (Re)^b (y/\delta)^c $$

(5)

$$ U/U_{\infty} = 10^m (Re)^n (y/\delta)^p $$

(6)

$$ \begin{aligned} f \delta/U_{\infty} & = 10^{-a} (Re)^{-b} (y/\delta)^{-c} (U/U_{\infty})\\ f \delta/U_{\infty} & = 10^{-a+m}(Re)^{-b+n} (y/\delta)^{-c+p} \end{aligned} $$

(7)

Conducting the power law fit using a robust least-squares approach, the parameters for the fit can be optimized for both Reynolds number based on momentum thickness, Re _θ, and based on friction velocity, Re _τ , shown in Table 1. From the standard errors, there appears to be no advantage to either inner or outer scaling, although the functional form of the Reynolds number is admittedly simple and the range of Reynolds numbers quite limited. The resulting fits, including a simplified evaluation using the mean Reynolds number, are shown in Eq. (4).

Table 1 Robust least-squares coefficients for power law models of dominant modulation in inner and outer scaling

A robust fit approach to fitting a power law to data involves iterating a standard, weighted least squared, and modifying the weights with each iteration using a bisquare function of the residuals. Even though most outliers in the ridgeline of the cospectral density maps were eliminated by using the extended Gaussian fits, this process tends to produce a fit that is still more robust against the effects of any remaining outliers.

$$ Co(f \delta/U_{\infty}; \alpha, \mu, \sigma, \phi) = \alpha \exp{\left( -\frac{(f \delta/U_{\infty} -\mu)^2}{2 \sigma^2} \right)} \cos{(\phi)} + (f \delta/U_{\infty}) \sin{(\phi)} $$

(8)

The resulting fitted power laws are shown above in Eq. (4).

The cospectral density maps to which the above fitting was applied were calculated by coherent averaging, as noted above. While the coherent averaging technique appeared to succeed in preserving the phase information, in principle, incoherent averaging should provide a smoother power spectral estimate, at the cost of the preserved phase, as noted in Lyons (2011). Recalculating the cospectral maps using incoherent averaging (not shown) indicates precisely the expected loss of phase information, but, surprisingly, the power appears noisier, although the peak for the dominant large-scale modulation appears roughly consistent. Recalling that the coherent averaging is equivalent to time-domain averaging, the coherently averaged time series is essentially the output of a low-pass filter. In particular, this low-pass filtering would tend to smooth the envelope of the small-scale signal beyond what the envelope rectification accomplished and thereby eliminate the smallest scales in the envelope. By eliminating the smallest-scale fluctuations, the amplitude modulation effect appears to be clarified.