Squared error-based shrinkage estimators of discrete probabilities and their application to variable selection

Abstract

In the paper we consider a new approach to regularize the maximum likelihood estimator of a discrete probability distribution and its application in variable selection. The method relies on choosing a parameter of its convex combination with a low-dimensional target distribution by minimising the squared error (SE) instead of the mean SE (MSE). The choice of an optimal parameter for every sample results in not larger MSE than MSE for James–Stein shrinkage estimator of discrete probability distribution. The introduced parameter is estimated by cross-validation and is shown to perform promisingly for synthetic dependence models. The method is applied to introduce regularized versions of information based variable selection criteria which are investigated in numerical experiments and turn out to work better than commonly used plug-in estimators under several scenarios.

Appendices

A Proof of Eq. (4)

Proof

First recall the form of $\lambda _{MSE}$ in (4):

$$\begin{aligned} \lambda _{MSE}= & {} \frac{\sum _x \Big (\mathrm{Var}({{\hat{p}}}^{(2)}(x))- \mathrm{Cov}( {{\hat{p}}}^{(1)}(x), {{\hat{p}}}^{(2)}(x))\Big )}{\sum _x {{\,\mathrm{{\mathbb {E}}}\,}}({{\hat{p}}}^{(1)}(x)- {{\hat{p}}}^{(2)}(x))^2}. \end{aligned}$$

Similarly to the proof of Lemma 1, we notice that $MSE(\lambda )$ is a quadratic function of $\lambda$:

$$\begin{aligned} MSE(\lambda )= & {} {{\,\mathrm{{\mathbb {E}}}\,}}\bigg (\sum _x (p(x)-{{\hat{p}}}_\lambda (x))^2 \bigg )= {{\,\mathrm{{\mathbb {E}}}\,}}\bigg (\sum _x \Big [\lambda ^2\left( {{\hat{p}}}^{(1)}(x) - {{\hat{p}}}^{(2)}(x)\right) ^2 \nonumber \\&\quad - 2\lambda \left( p(x)-{{\hat{p}}}^{(2)}(x)\right) \left( {{\hat{p}}}^{(1)}(x)- {{\hat{p}}}^{(2)}(x)\right) + \left( p(x) - {{\hat{p}}}^{(2)}(x)\right) ^2\Big ]\bigg ).\nonumber \\ \end{aligned}$$

(37)

Therefore, we obtain

$$\begin{aligned} \lambda _{MSE}=\frac{\sum _x {{\,\mathrm{{\mathbb {E}}}\,}}\left( p(x)-{{\hat{p}}}^{(2)}(x)\right) \left( {{\hat{p}}}^{(1)}(x)- {{\hat{p}}}^{(2)}(x)\right) }{\sum _x {{\,\mathrm{{\mathbb {E}}}\,}}\left( {{\hat{p}}}^{(1)}(x)- {{\hat{p}}}^{(2)}(x)\right) ^2} \end{aligned}$$

(38)

and as ${{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(2)}(x) = p(x)$, we have

$$\begin{aligned}\mathrm{Var}({{\hat{p}}}^{(2)}(x))={{\,\mathrm{{\mathbb {E}}}\,}}\left( {{\hat{p}}}^{(2)}(x) - p(x)\right) {{\hat{p}}}^{(2)}(x)\end{aligned}$$

and

$$\begin{aligned}\mathrm{Cov}({{\hat{p}}}^{(1)}(x),{{\hat{p}}}^{(2)}(x))={{\,\mathrm{{\mathbb {E}}}\,}}\left( {{\hat{p}}}^{(2)}(x) - p(x)\right) {{\hat{p}}}^{(1)}(x).\end{aligned}$$

$\square$

B Proof of Theorem 1

Proof

As ${{\hat{p}}}^{(2)}(x,y)$ is the maximum likelihood estimator of p(x, y), its variance and second moment is well known and we omit the proof. We prove first corrected formula for ${{\,\mathrm{{\mathbb {E}}}\,}}\left( p^{(1)}(x, y) \right) ^2$. We have

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}\left( {{\hat{p}}}^{(1)}(x, y) \right) ^2 = \frac{1}{n^4}{{\,\mathrm{{\mathbb {E}}}\,}}\left[ \sum \limits _{i} {\mathbb {I}}(X_i = x)\sum \limits _{i'} {\mathbb {I}}(X_{i'} = x)\sum \limits _{j} {\mathbb {I}}(Y_j = y)\sum \limits _{j'} {\mathbb {I}}(Y_{j'} = y) \right] . \end{aligned}$$

The contribution to the expected value of the summands on RHS depends on the number of elements of the set $A_1=\{i, i', j, j'\}$.

• $|A_1| = 1$ ($i=j=i'=j'$)

  The contribution is $np(x, y)/n^4$.

• $|A_1| = 2$

  We have four cases:

  • 1. $i = i', j = j', i \ne j$

    $n(n-1)p(x)p(y)/n^4$

  • 2. $i = j, i' = j', i \ne i'$ or $i = j', i = j', i \ne i'$. These two cases have the same contribution which equals:

    $n(n-1)p^2(x, y)/n^4$

  • 3. $i = i' = j, j \ne j'$ or $i = i' = j', j \ne j'$

    $n(n-1)p(x, y)p(y)/n^4$

  • 4. $i = j' = j, i \ne i'$ or $i' = j = j', i \ne i'$

    $n(n-1)p(x, y)p(x)/n^4$

• $|A| = 3$

  We have three cases:

  • 1. $i \ne i', j = j', j \ne i, j \ne i'$

    $n(n-1)(n-2)p^2(x)p(y)/n^4$

  • 2. $i = i', j \ne j', i \ne j, i \ne j'$

    $n(n-1)(n-2)p(x)p^2(y)/n^4$

  • 3. $i = j, i \ne i', j \ne j', i \ne j'$ (there are four cases like this—the remaining three have pairwise unequal indices except for one pair from $\{(i, j')$, $(i', j)$, $(i', j')\}$)

    $n(n-1)(n-2)p(x, y)p(x)p(y)/n^4$

• $|A_1| = 4$

  $n(n-1)(n-2)(n-3)p^2(x)p^2(y)/n^4$

Summing up all of the terms we obtain the formula in Theorem 2. Similarly, we prove the formula for ${{\,\mathrm{{\mathbb {E}}}\,}}({{\hat{p}}}^{(1)}(x,y){{\hat{p}}}^{(2)}(x,y))$:

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}({{\hat{p}}}^{(1)}(x,y){{\hat{p}}}^{(2)}(x,y)) = \frac{1}{n^3}{{\,\mathrm{{\mathbb {E}}}\,}}\left[ \sum \limits _{i} {\mathbb {I}}(X_i = x)\sum \limits _{j} {\mathbb {I}}(Y_j = y)\sum \limits _{k} {\mathbb {I}}(X_{k} = x){\mathbb {I}}(Y_{k} = y) \right] . \end{aligned}$$

We define $A_2=\{i, j, k\}$, and we have three cases:

• $|A_2| = 1$

  The contribution is $np(x, y)/n^3$.

• $|A_2| = 2$

  We have three cases with corresponding contributions:

  • 1. $i = j, i \ne k$

    $n(n-1)p^2(x,y)/n^3$

  • 2. $i = k, i \ne j$

    $n(n-1)p(x)p(x,y)/n^3$

  • 3. $j = k, j \ne i$

    $n(n-1)p(y)p(x,y)/n^3$

• $|A_2| = 3$

  $n(n-1)(n-2)p(x)p(y)p(x,y)/n^3$

To obtain the formula for covariance of ${{\hat{p}}}^{(1)}(x,y)$ and ${{\hat{p}}}^{(2)}(x,y)$, we need to compute ${{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(1)}(x,y)$ and then simply use

$$\begin{aligned} \mathrm{Cov}({{\hat{p}}}^{(1)}(x,y),{{\hat{p}}}^{(2)}(x,y)) = {{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(1)}(x,y){{\hat{p}}}^{(2)}(x,y) - {{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(1)}(x,y){{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(2)}(x,y). \end{aligned}$$

To this end we note that

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}{{\hat{p}}}^{(1)}(x,y)&= \frac{1}{n^2}{{\,\mathrm{{\mathbb {E}}}\,}}\left[ \sum \limits _{i} {\mathbb {I}}(X_i = x)\sum \limits _{j} {\mathbb {I}}(Y_j = y)\right] \\&= \left( np(x, y) + n(n-1)p(x)p(y)\right) / n^2. \end{aligned}$$

$\square$

C Asymptotic behaviour of $\lambda$

We state the result analogous to Theorems 3 and 4 which study asymptotic behaviour of theoretical minimisers $\lambda _{MSE}^{U}$ , $\lambda _{SE}^{U}$, $\lambda _{MSE}^{Ind}$ and $\lambda _{SE}^{Ind}$. Note that in cases when the distribution is not uniform or is not a product of its marginals n times theoretical minimisers tend to the same limits as their empirical counterparts. The behaviour of $\lambda _{MSE}^U$ and $\lambda _{SE}^U$ in the uniform case is much simpler as they are equal to 1, whereas $\lambda _{MSE}^{Ind} \rightarrow 1$ in the independent case. The only unresolved case is the behaviour of $\lambda _{SE}^{Ind}$ in the latter case. We include a partial result as the second part of (iv).

Theorem 5

We have the following convergences provided $n\rightarrow \infty$:

• (i) n$\lambda _{MSE}^U \rightarrow c$ when $p(x)\not \equiv 1/m,$ c defined in (22) and $\lambda _{MSE}^U =1$ otherwise;

• (ii) n$\lambda _{SE}^U \rightarrow c$ a.e. when $p(x)\not \equiv 1/m,$ c defined in (22), and $\lambda _{SE}^U =1$ otherwise;

• (iii) n$\lambda _{MSE}^{Ind} \rightarrow c,$ when $p(x,y)\not \equiv p(x)p(y),$ c defined in (27) and $\lambda _{MSE}^{Ind} \rightarrow 1$ otherwise;

• (iv) n $\lambda _{SE}^{Ind} \rightarrow c$ a.e. when $p(x,y)\not \equiv p(x)p(y),$ c defined in (27). Otherwise we have the following representation

  

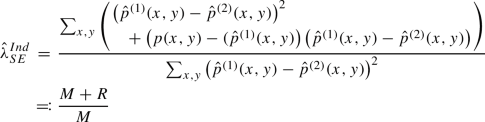
  and ${{\,\mathrm{{\mathbb {E}}}\,}}R =0,$ ${{\,\mathrm{{\mathbb {E}}}\,}}M = O(1/n)$

Proof

We prove the second part of (iv) only as the proofs of the remaining parts are analogous but simpler than those of Theorems 3 and 4. The second part of (ii) follows from checking that the leading terms in the numerator and the denominator of $\lambda _{MSE}^{Ind}$ (of order $n^{-1}$) are the same. We omit the details. In order to prove the second part of (iv) note that representation of $\lambda _{SE}^{Ind}$ follows from a simple calculation. Moreover, using independence we have

$$\begin{aligned} \mathrm{Var}({{\hat{p}}}^{(1)}(x,y))=\bigg (\frac{n-1}{n}p^2(x) +\frac{1}{n}p(x)\bigg )\bigg (\frac{n-1}{n}p^2(y) +\frac{1}{n}p(y)\bigg ) -p^2(x)p^2(y) \end{aligned}$$

and it is seen that it coincides with $\mathrm{Cov}(p^{(1)}(x,y),{{\hat{p}}}^{(2)}(x,y))$ (see Theorem 1). Additionally, it is easily seen that

$$\begin{aligned} \mathrm{Var}({{\hat{p}}}^{(2)}(x,y))- \mathrm{Var}({{\hat{p}}}^{(1)}(x,y))\ge \frac{c_1}{n} \end{aligned}$$

(39)

for some $c_1>0$. Thus we have

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}R= -\sum _{x,y}\mathrm{Var}({{\hat{p}}}^{(1)}(x,y)) + \mathrm{Cov}({{\hat{p}}}^{(1)}(x,y),{{\hat{p}}}^{(2)}(x,y))=0 \end{aligned}$$

whereas

$$\begin{aligned} {{\,\mathrm{{\mathbb {E}}}\,}}M= & {} \sum _{x,y}{{\,\mathrm{{\mathbb {E}}}\,}}\left( {{\hat{p}}}^{(1)}(x,y) - {{\hat{p}}}^{(2)}(x,y)\right) ^2= \sum _{x,y} \Big (\mathrm{Var}({{\hat{p}}}^{(1)}(x,y)) \\&\quad +\mathrm{Var}({{\hat{p}}}^{(2)}(x,y))- 2\mathrm{Cov}({{\hat{p}}}^{(1)}(x,y), {{\hat{p}}}^{(2)}(x,y))\Big ) \ge \frac{c_1}{n} \end{aligned}$$

which ends the proof of the second part of (iv).

$\square$

Remark 4

It follows from the proof of (iv) that in the case when X and Y are independent then

$$\begin{aligned}\mathrm{Var}({{\hat{p}}}^{(2)}(x,y))- \mathrm{Var}({{\hat{p}}}_{\lambda ^{Ind}_{SE}}(x,y))\ge \frac{c_1}{n}\end{aligned}$$

and thus shrinkage estimator has a smaller variance then ML estimator ${{\hat{p}}}^{(2)}$. This is intuitive as ${{\hat{p}}}^{(1)}$ is ML estimator in a smaller model assuming independence of X and Y and it has smaller variance then ${{\hat{p}}}^{(2)}$ [cf. (39)]. This property, which is likely to be preserved for approximate independence, is consistent with an aim of construction of James–Stein shrinkage estimators.