Frictional receding contact problem of a functionally graded layer resting on a homogeneous coated half-plane

Abstract

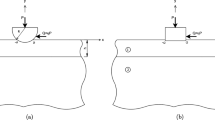
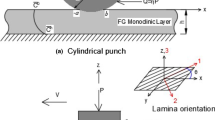
This paper investigates the frictional receding contact problem between a functionally graded (FG) layer resting on a homogeneous coated half-plane when the system indented by a rigid cylindrical punch. The shear modulus of the upper graded layer is assumed to vary exponentially in the depth direction. Upon loading, the advancing contact and receding contact occur between the FG layer and rigid punch and between the FG layer and coating, respectively. Under the assumptions of sliding contact, the shear and normal contact stresses are related through Coulomb’s law of friction. The contact problem is converted analytically using Fourier integral transforms and the proper boundary conditions into a system of two singular integral equations. The unknowns of these integral equations consist of the contact stresses under the punch and between the FG layer and coating as well as the dimensions of the contact zones. The Gauss–Jacobi quadrature collocation method is then employed to transform the singular integral equations into a system of nonlinear equations which are solved using an appropriate iterative algorithm to compute the contact stresses and the dimensions of the contact areas. The main purpose of this paper is to examine the influence of several parameters on the upper and lower contact stresses, which include the material inhomogeneity parameter, friction coefficient, punch radius, applied load, thickness of homogeneous layer, shear modulus of homogeneous layer and shear modulus of homogeneous half-plane. One of the most important conclusions from this study is that the contact stresses and contact areas can be controlled with the addition of the homogeneous layer.

Appendix A

1.1 Expressions of quantities appearing in integral equations (28a) and (28b)

$$\begin{aligned} k_{11} (x_1 ,t_1 )&= \int \limits _0^\infty {\frac{{I\;M_{11} (\alpha ) - \varphi _1 }}{{\varphi _1 }}} \sin \alpha (t_1 - x_1 )\mathrm{d}\alpha + \eta _1 \int \limits _0^\infty {\frac{{\;N_{11} (\alpha ) - \varphi _2 }}{{\varphi _1 }}} \cos \alpha (t_1 - x_1 )\mathrm{d}\alpha \end{aligned}$$

(A.1)

$$\begin{aligned} k_{12} (x_1 ,t_2 )&= \int \limits _0^\infty {\frac{{IM_{12} (\alpha )}}{{\beta _1 }}} \sin \alpha (t_2 - x_1 )\mathrm{d}\alpha + \eta _1 \int \limits _0^\infty {\frac{{N_{12} (\alpha )}}{{\beta _1 }}} \cos \alpha (t_2 - x_1 )\mathrm{d}\alpha \end{aligned}$$

(A.2)

where

$$\begin{aligned} M_{11} (\alpha )= & {} \sum \limits _{j = 1}^4 {\alpha m_{1j} e^{n_{1j} h_1 } A_{1j}^{p1} }, \quad N_{11} (\alpha ) = \sum \limits _{j = 1}^4 {\alpha m_{1j} e^{n_{1j} h_1 } A_{1j}^{q1} } \end{aligned}$$

(A.3)

$$\begin{aligned} M_{12} (\alpha )= & {} \sum \limits _{j = 1}^4 {\alpha m_{1j} e^{n_{1j} h_1 } A_{1j}^{p2} }, \quad N_{12} (\alpha ) = \sum \limits _{j = 1}^4 {\alpha m_{1j} e^{n_{1j} h_1 } A_{1j}^{q2} }. \end{aligned}$$

(A.4)

In Eq. (A.1), the singular terms $\varphi _1$ and $\varphi _2$ are given by

$$\begin{aligned} \varphi _1= & {} \mathop {\lim }\limits _{\alpha \rightarrow \infty } \;I\,M_{11} (\alpha ), \quad \varphi _2 = \mathop {\lim }\limits _{\alpha \rightarrow \infty } \;N_{11} (\alpha ) \end{aligned}$$

(A.5)

$$\begin{aligned} k_{21} (x_2 ,t_1 )= & {} \int \limits _0^\infty {\frac{{IM_{21} (\alpha )}}{{\beta _3 }}} \sin \alpha (t_1 - x_2 )\mathrm{d}\alpha + \eta _2 \int \limits _0^\infty {\frac{{N_{21} (\alpha )}}{{\beta _3 }}} \cos \alpha (t_1 - x_2 )\mathrm{d}\alpha \end{aligned}$$

(A.6)

$$\begin{aligned} k_{22} (x_2 ,t_2 )= & {} \int \limits _0^\infty {\frac{{I\;M_{22} (\alpha ) - \varphi _3 }}{{\varphi _3 }}} \sin \alpha (t_2 - x_2 )\mathrm{d}\alpha + \eta _2 \int \limits _0^\infty {\frac{{\;N_{22} (\alpha ) - \varphi _4 }}{{\varphi _3 }}} \cos \alpha (t_2 - x_2 )\mathrm{d}\alpha \end{aligned}$$

(A.7)

where

$$\begin{aligned} M_{21} (\alpha )= & {} \sum \limits _{j = 1}^4 { - \alpha \left( {m_{1j} A_{1j}^{p1} - m_{2j} A_{2j}^{p1} } \right) }, \quad N_{21} (\alpha ) = \sum \limits _{j = 1}^4 { - \alpha \left( {m_{1j} A_{1j}^{q1} - m_{2j} A_{2j}^{q1} } \right) } \end{aligned}$$

(A.8)

$$\begin{aligned} M_{22} (\alpha )= & {} \sum \limits _{j = 1}^4 { - \alpha \left( {m_{1j} A_{1j}^{p2} - m_{2j} A_{2j}^{p2} } \right) }, \quad N_{22} (\alpha ) = \sum \limits _{j = 1}^4 { - \alpha \left( {m_{1j} A_{1j}^{q2} - m_{2j} A_{2j}^{q2} } \right) }. \end{aligned}$$

(A.9)

In Eq. (A.7), the expressions of the singular terms $\varphi _3$ and $\varphi _4$ can be written as

$$\begin{aligned} \varphi _3 = \mathop {\lim }\limits _{\alpha \rightarrow \infty } \;I\;M_{22} (\alpha ), \quad \varphi _4 = \mathop {\lim }\limits _{\alpha \rightarrow \infty } \;N_{22} (\alpha ) \end{aligned}$$

(A.10)