On the formulation and evaluation of old and new efficient low order triangular plate bending elements with shear effects

Abstract

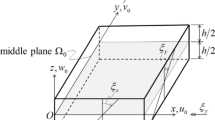
This paper deals with the presentation of a general, variational principle as theoretical support for the development of simple and efficient triangular elements having only one displacement and two rotations at the corner nodes to model thin to thick plates based on the first order Reissner- Mindlin plate theory. The functional is a modified Hellinger–Reissner mixed expression in terms of the kinematic variables (transverse displacement w and rotations βx and βy), and independent transverse shear strains (γx and γy). The approximations of the five independent variables of the mixed formulation take into account the accumulated knowledge on existing performing 2D Timoshenko beams and triangular elements such as T3γ_s, MITC3, DKT, DST, DKMT. The present mixed variational support is useful, not only to give a unique theoretical support to the above existing elements, usually based on assumed natural strain formulations, but it allows also to propose new simple and efficient elements, here called BAK1, BAK2 and BAK3. The paper includes a detailed presentation of results of patch tests for very thin and very thick plates, for convergence of displacements, bending moments and shear forces, for clamped circular and simply supported square plates and for s-norm convergence tests considering regular and irregular meshes. Shear force distribution is also considered for situations with boundary layer effects.

Appendices

Appendix A: 2D Timoskenko beam mixed FE model for an exact stiffness matrix

Consider a 2D beam finite element with $H_{b} = E \cdot I$ (the bending rigidity), $H_{s} = k \cdot G \cdot A$ (the shear rigidity), Query ID="Q4" Text="Please note that the Appendix section equations and their citations are renumbered to ensure sequential ordering." with $E$ and $G$ the Young and shear modulus, $I$ moment of inertia, A cross section.

The internal strain energy, for an element of length $L$ can be expressed in a mixed form as [1]:

$${\Pi }_{int}^{e} \left( {w, \beta , T} \right) = {\Pi }_{int}^{b} \left( { \beta } \right) + {\Pi }_{int}^{s} \left( {w, \beta , T} \right)$$

(A1)

with

$${\Pi }_{int}^{b} = \frac{1}{2} \cdot \mathop \int \limits_{0}^{L} \beta_{^{\prime}x} \cdot H_{b} \cdot \beta_{^{\prime}x} dx$$

(A2)

$${\Pi }_{int}^{s} = - \frac{1}{2} \cdot \mathop \int \limits_{0}^{L} T \cdot H_{s}^{ - 1} \cdot T dx + \mathop \int \limits_{0}^{L} T \cdot \gamma dx$$

(A3)

$w$: normal displacement along z; $\beta$: rotation of the cross section (in $xz$ plane).

$\gamma = w_{^{\prime}x} + \beta$: transverse shear (TS) strain; $T$: shear force (along $z$).

Without distributed load, the equilibrium equation along the $z$ direction can be expressed as:

$$T_{^{\prime}x} = 0$$

(A4)

Hence $T = T_{0}$ constant is sufficient as a $C^{ - 1}$ approximation at the element level. Consider a quadratic expression for $\beta \left( x \right)$, of the form:

$$\beta = N_{1} \cdot \beta_{1} + N_{2} \cdot \beta_{2} + 4 \cdot N_{1} \cdot N_{2} \cdot \Delta \beta$$

(A5)

with $N_{1} = 1 - \frac{x}{L}$; $N_{2} = \frac{x}{L}$; $\Delta \beta$ is the quadratic contribution of rotation at mid-node.

The curvature $\chi = \beta_{^{\prime}x}$ is then:

$$\chi = \left\langle {B_{1}^{b} } \right\rangle \cdot \left\{ {u_{n} } \right\} + B_{2}^{b} \cdot \Delta \beta$$

(A6)

with $\left\langle {B_{1}^{b} } \right\rangle = \left\langle {\begin{array}{*{20}c} 0 & { - \frac{1}{L}} & {\begin{array}{*{20}c} 0 & \frac{1}{L} \\ \end{array} } \\ \end{array} } \right\rangle$; $B_{2}^{b} = \frac{4}{L} \cdot \left( {1 - 2 \cdot \frac{x}{L}} \right)$; $\left\langle {u_{n} } \right\rangle = \left\langle {\begin{array}{*{20}c} {w_{1} } & {\beta_{1} } & {\begin{array}{*{20}c} {w_{2} } & {\beta_{2} } \\ \end{array} } \\ \end{array} } \right\rangle$.

Eq. A2 can be expressed in matrix form as:

$$\begin{aligned} {\Pi }_{int}^{b} & = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \right\rangle \cdot \mathop \int \limits_{0}^{L} \left( {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\left\{ {B_{1}^{b} } \right\}} \\ \cdots \\ {B_{2}^{b} } \\ \end{array} } \right\}} & {H_{b} } & {\left\langle {\begin{array}{*{20}c} {\left\langle {B_{1}^{b} } \right\rangle } & \vdots & {B_{2}^{b} } \\ \end{array} } \right\rangle } \\ \end{array} } \right)dx \left\{ {\begin{array}{*{20}c} {\left\{ {u_{n} } \right\}} \\ \ldots \\ {\Delta \beta } \\ \end{array} } \right\} \\ {\Pi }_{int}^{b} & = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \right\rangle \cdot \left[ {\begin{array}{*{20}c} {\left[ {k_{11}^{b} } \right]} & {\left\{ {k_{12}^{b} } \right\}} \\ {\left\langle {k_{12}^{b} } \right\rangle } & {k_{22} } \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {u_{n} } \\ \ldots \\ {\Delta \beta } \\ \end{array} } \right\} \\ \end{aligned}$$

(A7)

with $\left[ {k_{11}^{b} } \right] = \left\{ {B_{1}^{b} } \right\} \cdot H_{b} \cdot \left\langle {B_{1}^{b} } \right\rangle \cdot L$; $k_{22}^{b} = \frac{16}{{3 \cdot L}} \cdot H_{b} ; \left\{ {k_{12}^{b} } \right\} = \left\{ 0 \right\}$. or

$${\Pi }_{int}^{b} = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \right\rangle \cdot \left[ {\begin{array}{*{20}c} {\left[ {k_{11}^{b} } \right]} & {\left\{ 0 \right\}} \\ {\left\langle 0 \right\rangle } & {\frac{16}{{3 \cdot L}} \cdot H_{b} } \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {u_{n} } \\ \ldots \\ {\Delta \beta } \\ \end{array} } \right\};\,\left[ {k_{11}^{b} } \right] = \frac{{H_{b} }}{L} \cdot \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & { - 1} \\ 0 & 0 & 0 & 0 \\ 0 & { - 1} & 0 & 1 \\ \end{array} } \right]$$

(A8)

The internal shear energy can be expressed as:

$${\Pi }_{int}^{s} = - \frac{1}{2} \cdot T_{0} \cdot \frac{1}{{H_{s} }} \cdot T_{0} \cdot L + T_{0} \cdot \overline{\gamma }$$

(A9)

with

$$\overline{\gamma } = \frac{1}{L}\mathop \int \limits_{0}^{L} \gamma dx = \frac{1}{L}\left( {w_{2} - w_{1} + \frac{L}{2} \cdot \left( {\beta_{1} + \beta_{2} } \right) + \frac{2}{3} \cdot L \cdot \Delta \beta } \right) = \frac{1}{L}\left\langle a \right\rangle \cdot \left\{ {u_{n} } \right\} + \frac{2}{3} \cdot \Delta \beta$$

(A10)

with: $\left\langle a \right\rangle = \left\langle {\begin{array}{*{20}c} { - 1} & \frac{L}{2} & {\begin{array}{*{20}c} 1 & \frac{L}{2} \\ \end{array} } \\ \end{array} } \right\rangle$.

In matrix form:

$${\Pi }_{int}^{s} = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & \vdots & {\begin{array}{*{20}c} {T_{0} } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\rangle \cdot \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left\{ a \right\}L} & {\left\{ 0 \right\}} \\ {L\left\langle a \right\rangle } & { - \frac{L}{{H_{s} }}} & {\frac{2}{3} \cdot L} \\ {\left\langle 0 \right\rangle } & {\frac{2}{3} \cdot L} & 0 \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {\left\{ {u_{n} } \right\}} \\ {T_{0} } \\ {\Delta \beta } \\ \end{array} } \right\}$$

(A11)

The internal strain energy is then:

$${\Pi }_{int}^{e} = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & \vdots & {\begin{array}{*{20}c} {T_{0} } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\rangle \cdot \left[ {k_{0} } \right] \cdot \left\langle {\left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & \vdots & {\begin{array}{*{20}c} {T_{0} } & {\begin{array}{*{20}c} \vdots & {\Delta \beta } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\rangle } \right\rangle^{T}$$

(A12)

$$\left[ {k_{0} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {k_{11}^{b} } \right]} & {\left\{ a \right\}} & {\left\{ 0 \right\}} \\ {\left\langle a \right\rangle } & { - \frac{L}{{H_{s} }}} & {\frac{2}{3} \cdot L} \\ {\left\langle 0 \right\rangle } & {\frac{2}{3} \cdot L} & {\frac{16}{{3 \cdot L}} \cdot H_{b} } \\ \end{array} } \right]$$

Elimination of $\Delta \beta$ (internal variable) leads to:

$$\frac{2}{3} \cdot T_{0} \cdot L + \frac{16}{3} \cdot \frac{{H_{b} }}{L} \cdot \Delta \beta = 0\,{\text{or}}\,\Delta \beta = - \frac{{T_{0} \cdot L^{2} }}{{8 \cdot H_{b} }}$$

(A13)

Then the expression of ${\Pi }_{int}^{e}$ is:

$${\Pi }_{int}^{e} = \frac{1}{2} \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & \vdots & {T_{0} } \\ \end{array} } \right\rangle \cdot \left[ {k_{00} } \right] \cdot \left\langle {\begin{array}{*{20}c} {\left\langle {u_{n} } \right\rangle } & \vdots & {T_{0} } \\ \end{array} } \right\rangle^{T}$$

(A14)

with

$$\left[ {k_{00} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {k_{11}^{b} } \right]} & {\left\{ a \right\}} \\ {\left\langle a \right\rangle } & {\frac{{ - L^{3} }}{{12 \cdot H_{b} }} \cdot \left( {1 + \phi } \right)} \\ \end{array} } \right];\,\phi = \frac{{12 \cdot H_{b} }}{{L^{2} \cdot {\mathbf{H}}_{{\mathbf{s}}} }}$$

(A15)

Elimination of $T_{0}$ leads to:

$$T_{0} = \frac{{12 \cdot H_{b} }}{{L^{3} \cdot \left( {1 + \emptyset } \right)}} \cdot \left\langle a \right\rangle \cdot \left\{ {u_{n} } \right\} = \frac{{12 \cdot H_{b} }}{{L^{3} \cdot \left( {1 + \emptyset } \right)}} \cdot \left( {w_{2} - w_{1} + \frac{1}{2} \cdot \left( {\beta_{1} + \beta_{2} } \right)} \right)$$

(A16)

$${\Pi }_{int}^{e} = \frac{1}{2} \cdot \left\langle {u_{n} } \right\rangle \cdot \left[ k \right] \cdot \left\{ {u_{n} } \right\}$$

(A17)

with

$$\left[ k \right] = \left[ {k_{11}^{b} } \right] + \frac{{12 \cdot H_{b} }}{{L^{3} \cdot \left( {1 + \emptyset } \right)}} \cdot \left\{ a \right\} \cdot \left\langle a \right\rangle = \frac{{H_{b} }}{{L^{3} \cdot \left( {1 + \emptyset } \right)}} \cdot \left[ {\begin{array}{*{20}c} {12} & { - 6 \cdot L} & { - 12} & { - 6 \cdot L} \\ & {\left( {4 + \emptyset } \right) \cdot L^{2} } & {6 \cdot L} & {\left( {2 - \emptyset } \right) \cdot L^{2} } \\ & & {12} & {6 \cdot L} \\ & {sym} & & {\left( {4 + \emptyset } \right) \cdot L^{2} } \\ \end{array} } \right]$$

(A18)

The above stiffness is exact (it can represent the exact strain energy) and will lead to exact nodal values for $w$ and $\beta$ if an “exact” consistent load vector is used for distributed load along $x$. See [1] for more details. We add that an alternative formulation can be proposed, ending with the same stiffness matrix if an assumed transverse shear strain $\underline {\gamma }$ is used instead of the shear force $T$, but using $\underline {\gamma } = \frac{T}{{H_{s} }}$.

Appendix B: General expressions of shear strains using equilibrium equations: DST and DKMT revisited

a) The DST element proposed in 1989 [32] is based on the approximations for the rotations (Eq. 6) but the shear strains are defined using the equilibrium equations. Those independent cartesian shear strains are:

$${\underline {\boldsymbol{\gamma}}} = \left\{ {\begin{array}{*{20}c} {{\underline {\boldsymbol{\gamma}}}_{x} } \\ {{\underline {\boldsymbol{\gamma}}}_{y} } \\ \end{array} } \right\} = {\varvec{H}}_{s}^{ - 1} \cdot \left\{ {\begin{array}{*{20}c} {T_{x} } \\ {T_{y} } \\ \end{array} } \right\}$$

(A19)

$${\text{with}}\,\left\{ {\begin{array}{*{20}c} {T_{x} } \\ {T_{y} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {M_{x,x} + M_{xy,y} } \\ {M_{xy,y} + M_{y,y} } \\ \end{array} } \right\} = \overline{\bf{H}}_{b} \cdot \left\{ {\begin{array}{*{20}c} {\beta_{x,xx} + \beta_{x,yy} + \beta_{y,xy} } \\ {\beta_{x,yx} + \beta_{y,xx} + \beta_{y,yy} } \\ \end{array} } \right\}$$

Therefore:

$${\underline {\boldsymbol{\gamma}}} = {\varvec{B}}_{{s{\Delta }\beta }}^{DST} \cdot {\Delta }{\varvec{\beta}}_{sn}$$

(A20)

with

$$\begin{aligned} {\varvec{B}}_{{s{\Delta }\beta }}^{DST} & = {\varvec{H}}_{s}^{ - 1} \cdot \overline{\bf{H}}_{b} \cdot {\varvec{T}}_{j} \cdot {\varvec{T}}_{{{\Delta }\beta }} \\ \overline{H}_{b} & = D_{b} \cdot \left[ {\begin{array}{*{20}c} 1 & {\frac{1 - \upsilon }{2}} & 0 & 0 & 0 & {\frac{1 + \upsilon }{2}} \\ 0 & 0 & {\frac{1 + \upsilon }{2}} & {\frac{1 - \upsilon }{2}} & 1 & 0 \\ \end{array} } \right];D_{b} = \frac{{E\cdot h^{3} }}{{12\cdot\left( {1 - \gamma^{2} } \right)}} \\ {\varvec{T}}_{j} & = \left[ {\begin{array}{*{20}c} {{\varvec{t}}_{j} } & 0 \\ 0 & {{\varvec{t}}_{j} } \\ \end{array} } \right] \\ \left[ {{\varvec{t}}_{j} } \right] & = \frac{1}{{4 \cdot A^{2} }} \cdot \left[ {\begin{array}{*{20}c} {y_{13}^{2} } & {y_{21}^{2} } & {2 \cdot y_{13} \cdot y_{21} } \\ {x_{13}^{2} } & {x_{21}^{2} } & {2 \cdot x_{13} \cdot x_{21} } \\ { - y_{13} \cdot x_{13} } & { - y_{21} \cdot x_{21} } & { - y_{13} \cdot x_{21} - y_{21} \cdot x_{13} } \\ \end{array} } \right] \\ \left[ {{\varvec{t}}_{{{\Delta }\beta }} } \right] & = \left[ {\begin{array}{*{20}c} { - 8 \cdot C_{4} } & 0 & 0 \\ 0 & 0 & { - 8 \cdot C_{6} } \\ { - 4 \cdot C_{4} } & {4 \cdot C_{5} } & { - 4 \cdot C_{6} } \\ { - 8 \cdot S_{4} } & 0 & 0 \\ 0 & 0 & { - 8 \cdot S_{6} } \\ { - 4 \cdot S_{4} } & {4 \cdot S_{5} } & { - 4 \cdot S_{6} } \\ \end{array} } \right] \\ \end{aligned}$$

For DST the shear energy is then given by:

$${\Pi }_{int}^{s} = \frac{1}{2} \cdot \mathop \int \limits_{A} {\underline {\boldsymbol{\gamma}}}^{T} \cdot {\varvec{H}}_{s} \cdot {\underline {\boldsymbol{\gamma}}} dA = \frac{1}{2} \cdot {\Delta }{\varvec{\beta}}_{sn}^{T} \cdot {\varvec{k}}_{s}^{DST} \cdot {\Delta }{\varvec{\beta}}_{sn}^{T}$$

(A21)

$${\varvec{k}}_{s}^{DST} = \mathop \int \limits_{A} {\varvec{B}}_{{s{\Delta }\beta }}^{DST^{T}} \cdot {\varvec{H}}_{s} \cdot {\varvec{B}}_{{s{\Delta }\beta }}^{DST} dA = A\cdot{\varvec{B}}_{{s{\Delta }\beta }}^{DST^{T}} \cdot{\varvec{H}}_{s} \cdot{\varvec{B}}_{{s{\Delta }\beta }}^{DST}$$

On a side $k$ the assumed tangential shear strain is:

$$\underline {\gamma }_{sk} = C_{k} \cdot \underline {\gamma }_{x} + S_{k} \cdot \underline {\gamma }_{y} = \begin{array}{*{20}c} {C_{k} } & {S_{k} } \\ \end{array} \cdot {\varvec{B}}_{{{\text{s}{\Delta }}\beta }}^{DST} \cdot {\Delta }{\varvec{\beta}}_{sn}$$

(A22)

leading to:

$${\underline {\boldsymbol{\gamma}}}_{sn} = {\varvec{CS}} \cdot {\varvec{B}}_{{{\text{s}{\Delta }}\beta }}^{DST} \cdot {\Delta }{\varvec{\beta}}_{sn}$$

with

$${\varvec{CS}} = \left[ {\begin{array}{*{20}c} {C_{4} } & {S_{4} } \\ {C_{5} } & {S_{5} } \\ {C_{6} } & {S_{6} } \\ \end{array} } \right]$$

We impose the following constraints on each side:

$$\underline {\gamma }_{sk} = \frac{1}{{L_{k} }} \cdot \mathop \int \limits_{0}^{{L_{k} }} \gamma_{s} ds;\,{\text{with}}\,\gamma_{s} = w_{^{\prime}s} + \beta_{s}$$

(A23a)

Hence: $\gamma_{{{\text{sk}}}} = \frac{1}{{L_{k} }}\cdot\left( {w_{j} - w_{i} } \right) + \frac{1}{2} \cdot C_{k} \cdot \left( {\beta_{{x_{i} }} + \beta_{{x_{j} }} } \right) + \frac{1}{2} \cdot S_{k} \cdot \left( {\beta_{{y_{i} }} + \beta_{{y_{j} }} } \right) + \frac{2}{3} \cdot {\Delta }\beta_{sk}$.

and for the element:

$${\underline {\boldsymbol{\gamma}}}_{sn} = {\varvec{A}}_{u} \cdot {\varvec{u}}_{n} + \frac{2}{3} \cdot {\Delta }{\varvec{\beta}}_{sn}$$

(A23b)

Considering A22 and A23 we obtain:

$${\underline {\boldsymbol{\gamma}}}_{sn} = {\varvec{CS}}\cdot{\varvec{B}}_{{s{\Delta }\beta }}^{DST} \cdot{\Delta }{\varvec{\beta}}_{sn}$$

(A24a)

$${\Delta }{\varvec{\beta}}_{sn} = {\varvec{A}}_{{\Delta }}^{DST} \cdot {\varvec{A}}_{u} \cdot {\varvec{u}}_{n}$$

(A24b)

with ${\varvec{A}}_{{\Delta }}^{DST}$ a 3 × 3 full matrix: $\left( {{\varvec{A}}_{{{\Delta } }}^{DST} } \right)^{ - 1} = - \frac{2}{3}\cdot{\varvec{I}}_{3} + {\varvec{CS}}\cdot{\varvec{B}}_{{s{\Delta \beta}}}^{{{\varvec{D}}ST}}$.

The order of magnitude of ${\varvec{B}}_{{s{\Delta \beta}}}^{{{\varvec{D}}ST}}$ is ${\varvec{O}}\left( \phi \right)$ and ${\varvec{O}}\left( {\left( {{\varvec{A}}_{{{\Delta } }}^{DST} } \right)^{ - 1} } \right) = - \frac{2}{3}\cdot{\varvec{I}}_{3} + {\varvec{O}}\left( \phi \right)$.

Hence

$${\text{if}}\,\phi \to 0\,{\text{then}}\,{\varvec{A}}_{{{\Delta } }}^{DST} \to - \frac{3}{2}\cdot{\varvec{I}}_{3}$$

(A25)

as for DKT, so that shear locking is avoided for DST. On the other hand:

$${\text{if}}\,\phi \to \infty \,{\text{then}}\,\left( {{\varvec{A}}_{{{\Delta } }}^{DST} } \right)^{ - 1} \to - \frac{3}{2}\cdot{\varvec{I}}_{3} + {\varvec{O}}\left( \infty \right)\,{\text{and}}\,{\varvec{A}}_{{{\Delta } }}^{DST} \to {\varvec{O}}\left( {0_{3} } \right)$$

(A26)

as for $T3\gamma$. It was the same situation for BAK1 (§6). Since $\phi$ is never infinite, the risk is that some spurious bending $\left( {{\Delta }{\varvec{\beta}}_{{{\varvec{sn}}}} \ne 0} \right)$ exist for thick plates. This was observed and reported in [21, 40] for DST.

The stiffness matrix of a DST element is then:

$$\begin{aligned} {\varvec{k}} & = {\varvec{k}}_{b} + {\varvec{k}}_{s} \,{\text{with}} \\ {\varvec{k}}_{b} & = {\varvec{k}}_{11}^{b} + {\varvec{k}}_{12}^{b} \cdot{\varvec{A}}_{{\Delta }}^{DST} \cdot{\varvec{A}}_{u} + {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DST} } \right)^{T} \cdot{\varvec{k}}_{12}^{b^{T}} + {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DST} } \right)^{T} \cdot{\varvec{k}}_{22}^{b} \cdot{\varvec{A}}_{{\Delta }}^{DST} \cdot{\varvec{A}}_{u} \\ {\varvec{k}}_{s} & = {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DST} } \right)^{T} \cdot{\varvec{k}}_{s}^{DST} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DST} } \right)\cdot{\varvec{A}}_{u} \\ \end{aligned}$$

(A27)

with ${\varvec{k}}_{s}^{DST}$ given by Eq. A21.

b) Another possibility would have been to use the same shear strain energy as for $T3\gamma$ (Eq. 23)

$${\Pi }_{int}^{s} = \frac{1}{2} \cdot {\mathbf{\underline {\gamma } }}_{sn}^{T} \cdot {\varvec{k}}_{11}^{s} \cdot {\underline {\boldsymbol{\gamma}}}_{sn}$$

(A28)

but with full considerations of the equilibrium equations as for DST (A24) and (A25).

After programming it appears that using A28 instead of A21 we obtain the same stiffness matrix as for DST.

c) In [21], Katili proposed the DKMT element where he considers the equilibrium equation on a side k limited to (as for a beam):

$$\underline {\gamma }_{sk} = \frac{{T_{s} }}{{H_{s} }} = \frac{{M_{s,s} }}{{H_{s} }} = \frac{{D_{b} }}{{D_{s} }}\cdot\beta_{s,ss}$$

(A29)

With the expression of $D_{b} , D_{s}$ and the quadratic expression of $\beta_{s}$ on a side k, one obtains:

$$\underline {\gamma }_{sk} = - \frac{2}{3}\cdot\phi_{k} \cdot{\Delta \beta}_{{{\text{sk}}}}$$

(A30)

$${\text{with}}\,\phi_{k} = \frac{{12\cdot D_{b} }}{{D_{s} }}\cdot\left( {\frac{{h^{2} }}{{L_{k}^{2} }}} \right) = \frac{2}{{k\cdot\left( {1 - \nu } \right)}}\cdot\left( {\frac{{h^{2} }}{{L_{k}^{2} }}} \right)$$

Hence for an element:

$${\underline {\boldsymbol{\gamma}}}_{sn} = {\varvec{A}}_{\phi } \cdot{\Delta }{\varvec{\beta}}_{sn}$$

(A31)

$${\text{with}}\,{\varvec{A}}_{\phi } = - \frac{2}{3}\cdot\left[ {\begin{array}{*{20}c} {\phi_{4} } & 0 & 0 \\ 0 & {\phi_{5} } & 0 \\ 0 & 0 & {\phi_{6} } \\ \end{array} } \right]$$

with the constraint (eq. A23), so that:

$${\Delta }{\varvec{\beta}}_{sn} = {\varvec{A}}_{{\Delta }}^{DKMT} \cdot{\varvec{A}}_{u} \cdot{\varvec{u}}_{n}$$

(A32)

with

$$\left( {{\varvec{A}}_{{\Delta }}^{DKMT} } \right)^{ - 1} = - \frac{2}{3}\cdot{\varvec{I}}_{3} + {\varvec{A}}_{\phi }$$

$${\text{or}}\,{\varvec{A}}_{{\Delta }}^{DKMT} = - \frac{3}{2}\cdot\left[ {\begin{array}{*{20}c} {\frac{1}{{1 + \phi_{4} }}} & 0 & 0 \\ 0 & {\frac{1}{{1 + \phi_{5} }}} & 0 \\ 0 & 0 & {\frac{1}{{1 + \phi_{6} }}} \\ \end{array} } \right]$$

(A33)

$${\text{if}}\,\phi \to 0\,{\text{then}}\,{\varvec{A}}_{{{\Delta } }}^{DKMT} \to - \frac{3}{2}\cdot{\varvec{I}}_{3} \,\left( {\text{as for DKT and DST}} \right)$$

(A34)

$${\text{if}}\,\phi \to \infty \,{\text{then}}\,{\varvec{A}}_{{{\Delta } }}^{DKMT} \to \bf{ O}\left( {0_{3} } \right)({\text{as for}}\,T3\gamma )$$

(A35)

The conclusion is the same as for DST but the fact that ${\varvec{A}}_{{{\Delta } }}^{DKMT}$ is diagonal severely reduces the risk of bending locking for thick plates and in fact it is found that the constant curvature kinematical patch tests are exactly satisfied. This is not the case for DST for $L_{k} /h \ll 1$ (Figs. 4, 5). Despite that eq. A29 is an exact expression for beam, it is not a complete expression for a triangular domain. However, eq. A29 is statically consistent with the kinematical constant shear strain constraint on each side (eq. A23a, 23b).

The stiffness matrix of a DKMT element is:

$$\begin{aligned} {\varvec{k}} & = {\varvec{k}}_{b} + {\varvec{k}}_{s} \,{\text{with}} \\ {\varvec{k}}_{b} & = {\varvec{k}}_{11}^{b} + {\varvec{k}}_{12}^{b} \cdot{\varvec{A}}_{{\Delta }}^{DKMT} \cdot{\varvec{A}}_{u} + {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DKMT} } \right)^{T} \cdot{\varvec{k}}_{12}^{b^{T}} + {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DKMT} } \right)^{T} \cdot{\varvec{k}}_{22}^{b} \cdot{\varvec{A}}_{{\Delta }}^{DKMT} \cdot{\varvec{A}}_{u} \\ {\varvec{k}}_{s} & = {\varvec{A}}_{u}^{T} \cdot\left( {{\varvec{A}}_{{\Delta }}^{DKMT} } \right)^{T} \cdot{\varvec{A}}_{\phi }^{T} \cdot{\varvec{k}}_{11}^{s} \cdot{\varvec{A}}_{\phi } \cdot\left( {{\varvec{A}}_{{\Delta }}^{DKMT} } \right)\cdot{\varvec{A}}_{u} \\ \end{aligned}$$

(A36)

with ${\varvec{A}}_{\phi }$ and ${\varvec{A}}_{{\Delta }}^{DKMT}$ given by Eqs. A31 and A33.