Evaluation of three approaches to probable maximum precipitation estimation: a study on two Indian river basins

Abstract

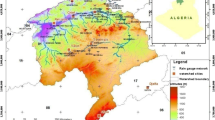
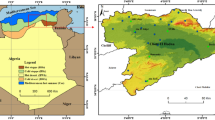
Estimates of probable maximum precipitation (PMP) and corresponding probable maximum flood (PMF) are necessary for planning, design, and risk assessment of flood control structures whose failure could have catastrophic consequences. For PMP estimation, multifractal approach (MA) is deemed to be better than conventional approaches, which are based either on statistical concepts or physical aspects. The MA yields physically meaningful PMP estimates by attempting to capture scale-invariant multiplicative cascade mechanism inherent in rainfall. This paper attempts to gain insights into the performance of MA by comparing PMP estimates obtained using the approach with those resulting from the use of two widely used empirical approaches (storm maximization approach (SMA) and Hershfield method (HM)) on two flood-prone river basins (Mahanadi and Godavari) in India. The results indicate that rainfall data of the two river basins exhibit multifractal properties, and the use of MA has an advantage over HM and SMA in estimating PMP corresponding to longer durations (>3 days). PMP estimates obtained using HM are generally lower (higher) than those obtained using SMA for 1-day (higher) duration. PMP maps are prepared for the two Indian river basins corresponding to 1-day to 5-day durations. Further, PMP estimates obtained based on the PMP maps are provided for 18 catchments in the Mahanadi basin and 53 catchments in the Godavari river basin.

Appendixes

1.1 Generalized extreme value distribution

The GEV distribution is a continuous probability distribution which is useful to model annual maximum values x₁, …, x_m extracted from the observed precipitation data. The cumulative distribution function F of the GEV distribution is of the form:

$$ F(x)=\left\{\begin{array}{l}\exp \left\{-{\left[1+k\frac{\left(x-\xi \right)}{\beta}\right]}^{-1/k}\right\}\kern0.5em \mathrm{for}\ k\ne 0\\ {}\exp \left\{-\exp \left[\frac{\left(x-\xi \right)}{\beta}\right]\right\}\kern2em \mathrm{for}\ k=0\end{array}\right. $$

(A1)

where ξ, β, and k are the location, scale, and shape parameters respectively (β > 0, ξ, k ∈ ℜ) and 1 + k(x − ξ)/β > 0. Estimates of the parameters are obtained in this study using the maximum likelihood method. Equation (A1) can be rearranged to get ${\hat{x}}_F$ (i.e., the quantile estimate of x) for any specified value of non-exceedance probability F (where 0 < F < 1).

$$ {\hat{x}}_F=\left\{\begin{array}{l}\hat{\xi}-\frac{\hat{\beta}}{\hat{k}}\left(1-{\left(-\log F\right)}^{-\hat{k}}\right),\kern0.75em \hat{k}\ne 0\\ {}\hat{\xi}-\hat{\beta}\log \left(-\log F\right)\kern2.5em \hat{k}=0\end{array}\right. $$

(A2)

The shape parameter k is important, as it determines the tail behavior of the distribution. If k > 0, it will correspond to Fréchet distribution, which has a long tail. If k = 0, it is referred to as Gumbel distribution whose tail is exponential. If k < 0, it will correspond to Weibull distribution with an upper limit for x. The sampling error caused by the limited sample data (observations on the extreme precipitation) is inevitable, which increases the uncertainty in $\hat{k}$ and consequently x_F that depends on $\hat{k}$. The uncertainty can be assessed by constructing the profile likelihood function to determine the confidence intervals of the shape parameter k and the quantile estimate x_F (e.g., Coles et al. 2001; Lu et al. 2013).

For a given value of precipitation (PMP), the corresponding return period T can be estimated in the case of GEV distribution as,

$$ T=\frac{1}{1-\exp \left\{-{\left[1+\frac{k}{\beta}\left(\mathrm{PMP}-\xi \right)\right]}^{-1/k}\right\}} $$

(A3)

1.2 Concept of profile likelihood function

In analysis with GEV distribution, the procedure to estimate confidence intervals of the shape parameter k and the quantile estimate x_F using profile likelihood function (Coles et al. 2001; Lu et al. 2013) involves the following steps.

• (1) Determine the maximum likelihood estimates of parameters $\left(\hat{\xi},\hat{\beta},\hat{k}\right)$ and quantile x_F of the GEV distribution, where $\hat{\xi}$ and $\hat{\beta}$ denote location and scale parameters, respectively.

Let x₁, …, x_m denote the data points in the annual maximum precipitation record. Construct the log-likelihood function to estimate parameters of GEV distribution. The function is given by Equation (A4) when k ≠ 0, and by Equation (A5) if k = 0.

$$ \mathrm{\ell}\left(\xi, \beta, k\right)=-m\log \beta -\left(1+1/k\right)\times \sum \limits_{i=1}^m\log \left[1+k\left(\frac{x_i-\xi }{\beta}\right)\right]-\sum \limits_{i=1}^m{\left[1+k\left(\frac{x_i-\xi }{\beta}\right)\right]}^{-1/k} $$

(A4)

$$ \mathrm{\ell}\left(\mu, \beta \right)=-m\log \beta -\sum \limits_{i=1}^m\left(\frac{x_i-\xi }{\beta}\right)-\sum \limits_{i=1}^m\exp \left\{-\left(\frac{x_i-\xi }{\beta}\right)\right\} $$

(A5)

Maximize the log-likelihood function to determine the maximum likelihood estimates of the parameters $\left(\hat{\xi},\hat{\beta},\hat{k}\right)$. Use the estimated values of the parameters in Equation (A2) to arrive at a quantile estimate x_F corresponding to non-exceedance probability F (where 0 < F < 1).

• (2) Determine profile likelihood estimate of the shape parameter k of GEV distribution.

Suppose the shape parameter k = k₀ ≠ 0 is a constant. Maximize the log-likelihood function given by Equation (A4) about ξ and β, repetitively in a certain range of k₀. For each value assumed for k₀, the maximum value of the likelihood function can be obtained. The profile likelihood function of k is constructed using the resulting information. Finally, an approximation of 1 − α confidence interval of k is determined by using ${C}_{\alpha }=\left\{k:2\left(\mathrm{\ell}\left(\hat{\xi},\hat{\beta},\hat{k}\right)-\underset{\xi, \alpha }{\max}\mathrm{\ell}\left(\xi, \beta, k\right)\right)\le {c}_{1-\alpha}\right\}$, where c_1 − α is 1 − α quantile of chi-square distribution with one degree of freedom.

• (3) Determine profile likelihood estimate of quantile x_F of GEV distribution

To obtain a profile likelihood estimate of annual maximum precipitation quantile x_F, redefine the parameters of GEV distribution by introducing x_F into the likelihood function. It can be achieved by rearranging Equation (A2) to get Equation (A6) and substituting Equation (A6) into Equation (A4) to derive the log-likelihood function of GEV as a function of (x_F, β, k).

$$ \xi =\left\{\begin{array}{l}{x}_F+\frac{\beta }{k}\left(1-{\left(-\log F\right)}^{-k}\right),\kern0.75em k\ne 0\\ {}{x}_F+\beta \log \left(-\log F\right)\kern2.5em k=0\end{array}\right. $$

(A6)

Finally, the profile likelihood estimate and confidence interval of quantile x_F of GEV distribution can be obtained by following the procedure described (for shape parameter k) in step (2).

1.3 Area weighted PMP for a catchment

To estimate PMP for the catchment of a stream gauge in a river basin, the following steps were executed.

• (1) Catchment of the gauge was delineated by processing SRTM DEM data using ArcHYDRO tools in the ArcGIS framework.

• (2) Area weighted PMP corresponding to 1-day to 5-day durations was estimated for the catchment based on PMP map prepared for the basin as,

$$ {\mathrm{PMP}}^{(c)}=\sum \limits_{i=1}^{N_c}{w}_i\times {\mathrm{PMP}}_i=\sum \limits_{i=1}^{N_c}\left(\frac{A_i^{(c)}}{CA}\right)\times {\mathrm{PMP}}_i $$

(A7)

where PMP^(c) denotes area-weighted PMP for a catchment c having area CA and comprising N_c grids, ${A}_i^{(c)}$ denotes the area of i-th grid (i = 1, …, N_c) contained in the catchment, and w_i is the weight assigned to PMP_i (i.e., PMP corresponding to i-th grid) as the ratio of ${A}_i^{(c)}$ to CA.