Time reversal and last passage time of diffusions with applications to credit risk management

Abstract

We study time reversal, last passage time and $h$-transform of linear diffusions. For general diffusions with killing, we obtain the probability density of the last passage time to an arbitrary level and analyse the distribution of the time left until killing after the last passage time. With these tools, we develop a new risk management framework for companies based on the leverage process (the ratio of a company asset process over its debt) and its corresponding alarming level. We also suggest how a company can determine the alarming level for the leverage process by constructing a relevant optimisation problem.

1 Introduction

In this paper, we study the last passage time to a specific state and time reversal of linear diffusions and consider their applications to credit risk management. Specifically, we deal with a general time-homogeneous transient linear diffusion process $X$ that is killed only at the boundary points. We address three problems concerning the diffusion $X$. First, we fix an arbitrary level which we denote by $\alpha$ and call “reference point” in the mathematical context or “alarming (or premonition) level” in the financial context. This is an entrance point to a certain region which we refer to as a dangerous zone. We study the distribution of the last passage time to this point. Second, we derive the distribution of the time between the last passage time to $\alpha$ and the killing time. Finally, we suggest how the level $\alpha$ of interest can be chosen as a solution to an optimisation problem in the context of credit risk management.

Last passage times of standard Markov processes are studied in Getoor and Sharpe [12] where they analyse the joint distribution of the last exit time of the process from a transient set and its location at that time. Pitman and Yor [25] study the density of the last exit time of regular linear diffusions on the positive axis with the scale function satisfying $s(0+)=-\infty$ and $s(\infty )<\infty$ by using Tanaka’s formula and apply the result to Bessel processes. We study last passage times in a general setting and employ the technique presented in Salminen [27], which uses the $h$-transform method. This technique is a fast and easy way to obtain an explicit formula. In Proposition 3.1, we treat various cases comprehensively, providing a method with which one can find the distribution of the last passage time of general diffusions, irrespective of the spatial relationship of the starting point and reference point, or whether the killing time is almost surely finite or not. The density of the last passage time to level $\alpha$ can be used for a premonition of imminent killing: how dangerous would it be if the process hits the level $\alpha$? We apply our mathematical results to the leverage process of a company which is a function of a regular time-homogeneous linear diffusion in our setting (see Sect. 2.2 for the financial model). We discuss this application in Sect. 1.1.

Sect. 3.2 is concerned with the time left until killing after the last passage time to $\alpha$. While the literature mostly deals with the total time spent in a dangerous zone, that is, the occupation time, we study the time after the last passage time to level $\alpha$. This is essential information for risk management and is one of the novel features of this section. Since this problem involves two random variables (last passage time and time of killing), it is complex; therefore, we use the reversed process of diffusions to make the problem simpler. See Sharpe [29] and Williams [30] for a specific example of time reversal and a recent account by Chung and Walsh [4, Chaps. 11 and 13]. Proposition 3.6 derives the distribution of the time left until killing (after the last passage time to $\alpha$) for a general diffusion $X$. For a Brownian motion with drift, we obtain a semi-explicit expression of the density of the time until killing in Proposition 3.9. To the best of our knowledge, there are no articles that handle this problem.

Finally, in Sect. 3.3, we suggest a method to choose an appropriate level $\alpha ^{*}$ for our general diffusion $X$. For this, we formulate an optimisation problem which we believe is new, using last passage time arguments and the occupation time distribution. This problem is constructed in the context of credit risk management, but can be applied to various problems.

1.1 Application to credit risk management framework

We continue this section by discussing the application of our theoretical results to risk management. We apply general results for a diffusion $X$ (Propositions 3.1 and 3.6) to the leverage process of a company. In our financial model (Sect. 2.2), the leverage process is a function of a regular time-homogeneous linear diffusion. We are interested in a certain threshold, denoted by $R^{*}$, of the company’s leverage ratio, an exit from which means an entry into a dangerous zone and leads to insolvency without returning to $R^{*}$. In our setting, the level $R^{*}$ for the leverage ratio is equivalent to a certain level $\alpha$ for the underlying diffusion; therefore, we continue the discussion using $\alpha$.

Elliott et al. [9] discuss the valuation of defaultable claims when the payoff depends on the last passage time of a firm’s value to a certain state (see also Jeanblanc and Rutkowski [14]). We study the last passage time to $\alpha$ (denoted by $\lambda _{\alpha }$) before insolvency for the leverage process and analyse its implications to credit risk. It is well known that $\lambda _{\alpha }$ is not a stopping time. We take this point into consideration by using the optional projection (see Remark 3.2). The last passage to $\alpha$ indicates that the company cannot recover to normal business conditions once this occurs. It is often the case that firms in financial distress cannot recover once the leverage ratio deteriorates to a certain level: the lack of creditworthiness makes it almost impossible to continue usual business relations with their contractors, suppliers, customers, creditors and investors, which further pushes the firm to the brink of insolvency. In this sense, $\alpha$ can be considered as a precautionary level, the passage of which triggers an alarm. While$\lambda _{\alpha }$is not a stopping time, the density in Corollary3.4enables us to calculate certain probabilities associated with$\lambda _{\alpha }$. We emphasise that all of these probabilities are calculated based on the current position of the leverage process and the information available up to current time. This is a novel approach to analysing the dynamics of the leverage ratio, and there are no other studies to the best of our knowledge. As we demonstrate by using the actual company data in Sect. 4.1, the probabilities associated with $\lambda _{\alpha }$ provide very useful information for risk management.

Together with $\lambda _{\alpha }$, we study the time left until insolvency after the leverage process passes $\alpha$ for the last time. There are no other studies that analyse this time interval. The expectation of this random variable can be computed at time zero based on the drift and volatility parameters of the leverage process. We obtain the density of the time until insolvency after $\lambda _{\alpha }$ semi-explicitly in Proposition 3.9. See Sect. 4.2 and Fig. 3, where we used the actual company data for the analysis.

Finally, the appropriate level of $\alpha ^{*}$ for the leverage ratio, the passing of which should trigger an alarm to the management, can be determined by solving the optimisation problem in Sect. 3.3. This problem involves the last passage time and occupation time of a dangerous zone. An example of a study related to our optimisation problem is by Gerber et al. [11] which models the surplus of the company by using a Brownian motion with drift and uses the Omega model to analyse the occupation time in the “red”. In Gerber et al. [11], the authors study the total time a Brownian motion with positive drift spends below zero and the relation between the Laplace transform of this occupation time and the probability of going bankrupt in finite time.

We believe that our paper can contribute to more refined credit risk management for companies, as illustrated in Sect. 4 with an empirical analysis. The risk-free rates were obtained from the website of the US Department of the Treasury and the remaining data for the estimation was obtained from Thomson Reuters Datastream.

2 Mathematical framework

Let us consider a probability space $(\Omega , \mathcal{F}, \mathbb{P})$, where $\Omega$ is the set of all possible realisations of the stochastic economy and ℙ is a probability measure defined on ℱ. We denote by $\mathbb{F}=(\mathcal{F}_{t})_{t\ge 0}$ a filtration satisfying the usual conditions and consider a regular time-homogeneous transient diffusion process $X$ adapted to $\mathbb{F}$. The state space of $X$ is $\mathcal{I}:=(\ell , r)\subseteq \mathbb{R}$, and we adjoin an isolated point $\Delta$ to ℐ. We call $\omega$ a sample path from $[0, \infty )\to \mathcal{I}\cup \Delta$ with coordinates $\omega (t)=X_{t}(\omega )$. The lifetime of $X$ is defined by $\zeta (\omega ):=\inf \{t\ge 0: X_{t}(\omega )\notin \mathcal{I}\}$. Killing is not allowed inside ℐ and $X$ is killed only when it hits the boundary point $\ell$ or $r$. When killing occurs, the diffusion is immediately transferred to $\Delta$. Let $\mathbb{P}_{y}$ denote the probability measure associated to $X$ when started at $y\in \mathcal{I}$. Let $(P_{t})_{t\ge 0}$ be the transition semigroup of $X$. As in Karlin and Taylor [17, Chap. 15, Sect. 6], we assume $X$ has continuous infinitesimal drift and variance coefficients $\mu (x)$ and $\sigma ^{2}(x)>0$ on $x\in \mathcal{I}$, respectively. Also as in Karlin and Taylor [17, Chap. 15, Sect. 9], we assume that

$$ \lim _{h\downarrow 0} \frac{\mathbb{E}[|X_{t+h}-X_{t}|^{r}\vert X_{t}=x]}{h}=0, \qquad r=3,4, \dots $$

The generator is defined by $\mathfrak{G}f(x):=\mu (x)f'(x)+\frac{1}{2}\sigma ^{2}(x)f''(x)$ for a twice continuously differentiable function $f(x)$ on ℐ. Let the first passage time be denoted by $T_{x}:=\inf \{t\ge 0: \omega (t)=x\}$ for $x\in \mathcal{I}$. For $\ell < a\le y\le b< r$, the scale function $s(\cdot )$ of $X$, defined on $\mathcal{I}=(\ell ,r)$, satisfies

$$ \mathbb{P}_{y}[T_{a}< T_{b}]=\frac{s(b)-s(y)}{s(b)-s(a)}. $$

We denote the speed measure by $m(\cdot )$. For more information about diffusion processes, see e.g. Borodin and Salminen [3, Chap. II].

2.1 $h$-transform

Let $h$ be an excessive function; that is, $h$ is a nonnegative Borel-measurable function with the properties

$$\begin{aligned} &h\ge P_{t} h, \quad \forall t\ge 0 \qquad \text{and}\qquad h=\lim _{t \downarrow 0}P_{t} h. \end{aligned}$$

For a Borel-measurable set $A\in \mathcal{B}(\mathcal{I})$, define for $u, v\in \mathcal{I}$

$$ P^{h}_{t}(u, A):=\frac{1}{h(u)}\int _{A} h(v) P_{t}(u, {\mathrm {d}}v). $$

(2.1)

The $h$-transform of $X$ is a regular diffusion with the transition function (2.1) (Borodin and Salminen [3, Chap. II, Sect. 5]). Following Salminen [28], let us call an excessive function $h$minimal if the $h$-transform of $X$ converges $\mathbb{P}^{h}_{.}$-a.s. to a single point, that is, for all $y\in \mathcal{I}$,

$$ \mathbb{P}_{y}^{h}\Big[\lim _{t\rightarrow \zeta }X_{t}=z\Big]=1 $$

for some $z\in [\ell , r]$. Note that $\mathbb{P}_{y}^{h}$ is the probability law of the $h$-transform of $X$ starting at $y$.

2.2 Leverage process

We use the structural approach proposed by Merton [22] and analyse the credit-worthiness of a company through the behaviour of its unobservable asset process (the firm’s value). This approach models the firm’s value as a geometric Brownian motion and assumes the company equity is a European call option written on the asset process with a strike price equal to the value of debt at maturity. The structural approach is widely implemented in practice, and one of the examples is the expected default frequency (EDF) model provided by Moody’s analytics. For more information about structural models, we refer the reader to McNeil et al. [21, Sect. 10.3].

Suppose that a firm has total assets with market value $A=(A_{t})_{t\ge 0}$. We assume that the asset process $A$ follows a geometric Brownian motion with parameters $\nu \in \mathbb{R}$ and $\sigma >0$, and the debt process $D=(D_{t})_{t\ge 0}$ grows at a constant rate $r_{D}$, i.e.,

$$ A_{t}=A_{0}e^{\nu t+\sigma B_{t}^{A}} \qquad \text{and}\qquad D_{t}=D_{0}e^{r_{D}t}, $$

where we set the initial values as $A_{0}$ and $D_{0}$, respectively, and $B^{A}=(B_{t}^{A})_{t\geq 0}$ denotes a standard Brownian motion on $(\Omega , \mathcal{F},\mathbb{P})$ adapted to the filtration $\mathbb{F}$. Assuming $A_{0}>D_{0}$, we define the leverage process $R=(R_{t})_{t\ge 0}$ as $R_{t} := \frac{A_{t}}{D_{t}}$. Then we set the insolvency time of the firm as

$$ T:=\inf \{t\ge 0: R_{t} =1\}, $$

and $R_{T}=1$ implies

$$ \frac{\nu -r_{D}}{\sigma }T+B_{T}^{A}=\frac{1}{\sigma }\ln \frac{D_{0}}{A_{0}}=:c, $$

which means that the insolvency time is the first passage time to the state $c$ of a Brownian motion with drift $\frac{\nu -r_{D}}{\sigma }$ and unit variance parameter. Consequently, our study about the leverage process $R$ can be reduced to the study of a Brownian motion with drift and unit variance parameter, given by

$$ X_{t}:=y+ \frac{\nu -r_{D}}{\sigma } t + B_{t}^{A}, \qquad t\ge 0, $$

(2.2)

on the state space $\mathcal{I}':=(c, \infty )$. It follows that $y=0$ in our model; however, we continue the discussion for an arbitrary $y$ for the purpose of making general statements. We have

$$ T=T_{c}:=\inf \{t\ge 0: y+\mu t + B_{t}^{A}=c\} \qquad \mbox{with } \mu :=\frac{\nu -r_{D}}{\sigma }. $$

(2.3)

Since the stopping time $T$ is predictable, it is possible and may be a good idea to set a threshold level $R^{*}$ for the leverage process, so that when it passes this point from above, the firm should prepare and start precautionary measures to avoid possible subsequent insolvency. Also $R_{t}=R^{*}$ means that $X_{t}=\frac{1}{\sigma }\ln \frac{R^{*} D_{0}}{A_{0}}=:\alpha$, and we can again study the passage time to this arbitrary $\alpha \in (c, \infty )$ for a Brownian motion with drift starting from $y$.

We discuss and prove our results for a generic diffusion $X$ together with an application to our process (2.2). While we use the same $X$ for a general diffusion and the specific leverage process, we have made sure that the reader would not be confused.

3 Mathematical results

Let $X$ be a general diffusion as in Sect. 2. We consider two cases: $s(\ell )>-\infty$ and $s(r)=+\infty$ (Case 1) and $s(\ell )>-\infty$ and $s(r)<+\infty$ (Case 2). The left boundary can be exit, natural or regular. The right boundary can be either entrance or natural in Case 1 and exit, natural or regular in Case 2.

3.1 The last passage time

Let $\lambda _{x}=\sup \{t\geq 0: \omega (t)=x\}$ denote the last passage time to the level $x$ with the convention $\sup \emptyset =0$. Before deriving the distribution of $\lambda _{x}$, let us introduce some objects that are needed.

Case 1. The Green function (see Borodin and Salminen [3, Chap. II] for the definition) is

$$ G(y, z)=\int _{0}^{\infty }p(t; y, z){\mathrm {d}}t=\big(s(y)-s(\ell )\big) \wedge \big(s(z)-s(\ell )\big), \qquad y, z\in \mathcal{I}, $$

(3.1)

where $p(t; y, z)$ is the transition density of $X$ with respect to the speed measure so that $\mathbb{P}_{y}[X_{t}\in {\mathrm {d}}z]=p(t;y,z)m({\mathrm {d}}z)$. The functions $k_{\ell }$, $k_{r}$ and $k_{x}$ given by

$$\begin{aligned} k_{\ell }(x)&=1, \qquad k_{r}(x)=s(x)-s(\ell ) \end{aligned}$$

(3.2)

and

$$ k_{x}(y):=\min \left (k_{\ell }(y),\frac{k_{r}(y)}{s(x)-s(\ell )} \right )=\mathbb{P}_{y}[\lambda _{x}>0]= \textstyle\begin{cases} \frac{s(y)-s(\ell )}{s(x)-s(\ell )}, & y\leq x, \\ 1, & y>x, \end{cases} $$

(3.3)

with $x,y \in \mathcal{I}$, are minimal excessive. The excessiveness in (3.2) is because the functions are harmonic (see Dynkin [8, Theorem 12.4]). Now, $k_{\ell }(x)=1$ is minimal because $X$ converges to the boundary point $\ell$, that is, $\mathbb{P}_{y}[\lim _{t\rightarrow \zeta }X_{t}=\ell ]=1$ for all $y\in \mathcal{I}$. Next, the $k_{r}$-transform of $X$ is a regular diffusion with a transition function as in (2.1) with $h$ replaced by $k_{r}$. Its scale function is $s^{r}(x)=-\frac{1}{s(x)-s(\ell )}$. Then we can see that for all $y\in \mathcal{I}$, we have $\mathbb{P}_{y}^{k_{r}}[\lim _{t\rightarrow \zeta } X_{t}=r]=1$ since $s^{r}(\ell )=-\infty$. Finally, $k_{x}$ is excessive since it is the minimum of two excessive functions (see Chung and Walsh [4, Proposition 3.2.2]). The $k_{x}$-transform of $X$ is a regular diffusion with the transition function (2.1) with $h$ replaced by $k_{x}$. It can be seen that

$$\begin{aligned} &\text{The $k_{x}$-transform (or $k_{x}$-diffusion) is identical in law} \\ &\text{with $X$ conditioned to hit $x$ and be killed at its last exit time from $x$.} \end{aligned}$$

(3.4)

Indeed, for any $u,v\in \mathcal{I}$, the transition density $\bar{p}$ of such a conditioned diffusion with respect to the speed measure $\bar{m}$ satisfies

where $m$ denotes the speed measure of the original diffusion $X$ and $\theta (\cdot )$ is the shift operator (see also Meyer et al. [23, Theorem 2.1]). It follows that for all $x\in \mathcal{I}$, $\mathbb{P}_{y}^{k_{x}}[\lim _{t\rightarrow \zeta } X_{t}=x]=1$, so that $k_{x}$ is minimal.

Case 2. The minimal excessive functions $k_{\ell }$, $k_{r}$ and $k_{x}$ are

$$\begin{aligned} k_{\ell }(x)=s(r)-s(x), \qquad k_{r}(x)=s(x)-s(\ell ) \end{aligned}$$

(3.5)

and

$$k_x(y)=\{\begin{array}{cc}\frac{s(y)-s(\ell )}{s(x)-s(\ell )},& y\le x,\\ \frac{s(r)-s(y)}{s(r)-s(x)},& y>x,\end{array}$$

with $x, y\in \mathcal{I}$ (see e.g. Salminen [28, Theorem 2.10]). The Green function for $X$ is

$$G(y,z)={\int }_0^{\mathrm{\infty }}p(t;y,z)\mathrm{d}t=\{\begin{array}{cc}\frac{(s(y)-s(\ell ))(s(r)-s(z))}{s(r)-s(\ell )},& \ell <y\le z<r,\\ \frac{(s(z)-s(\ell ))(s(r)-s(y))}{s(r)-s(\ell )},& \ell <z\le y<r,\end{array}$$

where $p(t; y, z)$ is the transition density with respect to the speed measure so that $\mathbb{P}_{y}[X_{t}\in {\mathrm {d}}z]=p(t;y,z)m({\mathrm {d}}z)$.

We have the following result concerning the distribution of $\lambda _{x}$ for a general $X$ that complements Proposition 4 and Corollary 6 in Salminen [27]. Indeed, in the proof we provide detailed techniques applicable to various cases, which depend upon whether $s(r)$ is finite or infinite, and whether $\mathbb{P}_{y}[T_{x}<\infty ]$ is equal to or less than 1.

Proposition 3.1

Let$X$be a general diffusion process as in Sect. 2. We have for Case 1 and Case 2 for any$y, x\in \mathcal{I}$the result that

$$\begin{aligned} &\mathbb{P}_{y}[\lambda _{x}\in {\mathrm {d}}t,\lambda _{x}>0,T_{\ell }< T_{r}]= \frac{p(t; y, x)}{s(x)-s(\ell )}{\mathrm {d}}t , \end{aligned}$$

where$p(t; y, x)$is the transition density of$X$with respect to the speed measure$m(\cdot )$.

Remark 3.2

Since the last passage time $\lambda _{x}$ is not a stopping time, we use the optional projection (see Rogers and Williams [26, Chap. 6, Sect. 3]) to make it informative at an arbitrary fixed time $t$. Specifically, we consider the optional projection of on the filtration $\mathbb{F}$, given at $t$ by $\mathbb{P}_{y}[\lambda _{x}>t\vert \mathcal{F}_{t}]$ which is $\mathcal{F}_{t}$-measurable. We have

Note that since $s(r)=+\infty$ in Case 1, we have if $X_{t}>x$. We use both Proposition 3.1 and Remark 3.2 in the credit risk management application.

Proof of Proposition 3.1

For both cases, by observing that

$$ \mathbb{P}_{y}[\lambda _{x}\in {\mathrm {d}}t, \lambda _{x}>0, T_{\ell }< T_{r}]= \mathbb{P}_{y}[\lambda _{x}\in {\mathrm {d}}t, \lambda _{x}>0 \lvert T_{ \ell }< T_{r}] \mathbb{P}_{y}[T_{\ell }< T_{r}], $$

(3.6)

we consider the conditioned diffusion $X^{*}$ that visits $\ell$ in finite time. This condition is equivalent to the condition $T_{\ell }< T_{r}$ which in turn implies $\lim _{t\to \zeta }X_{t}=\ell$. By the Markov property, the transition density of $X^{*}$ with respect to the speed measure satisfies

$$\begin{aligned} p^{*}(t;u,v)m^{*}({\mathrm {d}}v)=\mathbb{P}_{u}[X_{t}\in {\mathrm {d}}v \lvert T_{ \ell }< T_{r}]=p(t;u,v)m({\mathrm {d}}v)\frac{s(r)-s(v)}{s(r)-s(u)}, \end{aligned}$$

where $m$ denotes the speed measure of the original diffusion $X$. Note that this is the same as the $k_{\ell }$-transform (see (3.2) and (3.5)). Let $\mathbb{P}^{*}$ denote the probability law of $X^{*}$. Since $s(r)=+\infty$ in Case 1, $T_{\ell }< T_{r}$ a.s. Using a Taylor expansion of the scale functions (see Karlin and Taylor [17, Chap. 15, Sect. 9]), we obtain

$$ s^{*}(x)=\left \{ \textstyle\begin{array}{llll} s(x) & \quad \mbox{in Case 1}, \\ \frac{1}{s(r)-s(x)} &\quad \mbox{in Case 2}, \end{array}\displaystyle \right . \quad \,\,\, m^{*}({\mathrm {d}}x)=\left \{ \textstyle\begin{array}{llll} m({\mathrm {d}}x) & \quad \mbox{in Case 1}, \\ (s(r)-s(x))^{2}m({\mathrm {d}}x) & \quad \mbox{in Case 2}, \end{array}\displaystyle \right . $$

(3.7)

and the transition density with respect to the speed measure $m^{*}(\cdot )$ is

$$ p^{*}(t;u,v)=\left \{ \textstyle\begin{array}{llll} p(t; u,v) & \quad \mbox{in Case 1}, \\ \frac{p(t;u,v)}{(s(r)-s(v))(s(r)-s(u))} & \quad \mbox{in Case 2}. \end{array}\displaystyle \right . $$

(3.8)

First, we are interested in the case when $X^{*}$ starts at $y\ge x$. Then $X^{*}$ will hit $x$ a.s. and the last exit time distribution from $x$ and the lifetime distribution of its $k_{x}$-transform coincide (see e.g. (3.4)). Thus we have to compute the lifetime distribution of the $k_{x}$-transform of $X^{*}$. By considering $X^{*}$ in space-time and following the argument of Martin boundary theory in the proof of Salminen [27, Proposition 4]), we obtain for $y\geq x$ that

$$ (\mathbb{P}_{y}^{*})^{k_{x}}[\zeta \in {\mathrm {d}}t]=\mathbb{P}_{y}^{*}[ \lambda _{x}\in {\mathrm {d}}t,\lambda _{x}>0]= \frac{p^{*}(t; y, x)}{G^{*}(y, x)}{\mathrm {d}}t= \frac{p^{*}(t; y, x)}{s^{*}(x)-s^{*}(\ell )}{\mathrm {d}}t $$

(see (3.1)). Now, $\mathbb{P}_{y}[T_{\ell }< T_{r}]=\frac{s(r)-s(y)}{s(r)-s(\ell )}$ and from (3.6),

$$\begin{aligned} \mathbb{P}_{y}[\lambda _{x}\in {\mathrm {d}}t, \lambda _{x}>0, T_{\ell }< T_{r}] &=\mathbb{P}_{y}^{*}[\lambda _{x}\in {\mathrm {d}}t, \lambda _{x}\!>\!0] \mathbb{P}_{y}[T_{\ell }< T_{r}] =\frac{p(t;y,x)}{s(x)-s(\ell )}{\mathrm {d}}t, \end{aligned}$$

where we used (3.7) and (3.8).

Now let $y< x$. We need the following lemma, which is of interest in its own right.

Lemma 3.3

Let$y< x$and consider the diffusion$X$in Case 1. Starting from$y$, the$k_{x}$-transform of$X^{k_{r}}$ (the$k_{r}$-transform of$X$) and the$k_{x}$-transform of$X$are identical in law.

Proof

The scale function $s^{r}$, speed measure $m^{r}$ and transition density $p^{r}(t; y, x)$ (with respect to $m^{r}$) of $X^{k_{r}}$ are written as

$$\begin{aligned} s^{r}(x)&=-\frac{1}{s(x)-s(\ell )}, \qquad m^{r}({\mathrm {d}}x)=\big(s(x)-s( \ell )\big)^{2} m({\mathrm {d}}x), \end{aligned}$$

(3.9)

$$\begin{aligned} p^{r}(t;y,x)&=\frac{p(t;y,x)}{(s(y)-s(\ell ))(s(x)-s(\ell ))}. \end{aligned}$$

(3.10)

We have

$$\begin{aligned} (\mathbb{P}^{k_{r}}_{y})^{k_{x}}[X_{t}\in A]&=\int _{A}p^{r}(t;y,u)m^{r}({ \mathrm {d}}u) \frac{\mathbb{P}_{u}^{r}[\lambda _{x}>0]}{\mathbb{P}_{y}^{r}[\lambda _{x}>0]} \\ &=\int _{A}p(t;y,u)m({\mathrm {d}}u)\frac{s(u)-s(\ell )}{s(y)-s(\ell )} \frac{\mathbb{P}^{r}_{u}[\lambda _{x}>0]}{1} \\ &=\left \{ \textstyle\begin{array}{llll} \int _{A}p(t;y,u)m({\mathrm {d}}u)\frac{s(u)-s(\ell )}{s(y)-s(\ell )}, & \quad u< x, \\ \int _{A}p(t;y,u)m({\mathrm {d}}u)\frac{s(u)-s(\ell )}{s(y)-s(\ell )} \frac{s^{r}(r)-s^{r}(u)}{s^{r}(r)-s^{r}(x)}, & \quad u\geq x, \end{array}\displaystyle \right . \\ &=\left \{ \textstyle\begin{array}{llll} \int _{A}p(t;y,u)m({\mathrm {d}}u)\frac{s(u)-s(\ell )}{s(y)-s(\ell )}, & \quad u< x, \\ \int _{A}p(t;y,u)m({\mathrm {d}}u)\frac{s(x)-s(\ell )}{s(y)-s(\ell )}, & \quad u\geq x, \end{array}\displaystyle \right . \\ &=\int _{A}p(t;y,u)m({\mathrm {d}}u) \frac{\mathbb{P}_{u}[\lambda _{x}>0]}{\mathbb{P}_{y}[\lambda _{x}>0]}= \mathbb{P}^{k_{x}}_{y}[X_{t}\in A]. \end{aligned}$$

In the first line, we used the definition of $k_{x}(\cdot )$ in (3.3) and (3.10). For the third line, we used $s(r)=+\infty$ in computing $s^{r}(r)=0$. □

From Lemma 3.3 and (3.4), we obtain that the lifetime of the $k_{x}$-transform of $X^{*}$ and the last exit time from $x$ for the $k_{r}$-transform of $X^{*}$ have the same distribution. Now $(X^{*})^{k_{r}}$ converges to $r$ a.s. and starting from $y< x$, $(X^{*})^{k_{r}}$ visits the level $x$ a.s. Hence we can argue as in the previous case (i.e., $x>y$) with $X^{*}$ replaced by $(X^{*})^{k_{r}}$. In particular, the last passage time to $x$ has the distribution

$$\begin{aligned} (\mathbb{P}^{*}_{y})^{k_{r}}[\lambda _{x}\in {\mathrm {d}}t]=(\mathbb{P}_{y}^{*})^{k_{x}}[ \zeta \in {\mathrm {d}}t] &=\frac{(p^{*})^{r}(t;y;x)}{(G^{*})^{r}(y,x)}{ \mathrm {d}}t \\ &=\frac{(p^{*})^{r}(t;y;x)}{(s^{*})^{r}(r)-(s^{*})^{r}(x)}{\mathrm {d}}t = \frac{p^{*}(t;y,x)}{s^{*}(y)-s^{*}(\ell )}{\mathrm {d}}t. \end{aligned}$$

In sum, for $y< x$, the last passage time to $x$ for $X^{*}$ has an atom at 0 since it may happen that $X^{*}$ does not hit $x$ at all. The continuous part is given by

$$\begin{aligned} \mathbb{P}_{y}^{*}[\lambda _{x}\in {\mathrm {d}}t,\lambda _{x}>0]&= \mathbb{P}_{y}^{*}[\lambda _{x}\in {\mathrm {d}}t\lvert \lambda _{x}>0] \mathbb{P}_{y}^{*}[\lambda _{x}>0] \\ &=(\mathbb{P}_{y}^{*})^{k_{x}}[\zeta \in {\mathrm {d}}t] \mathbb{P}_{y}^{*}[T_{x}< T_{ \ell }] \\ &=\frac{p^{*}(t;y,x){\mathrm {d}}t}{s^{*}(y)-s^{*}(\ell )} \frac{s^{*}(y)-s^{*}(\ell )}{s^{*}(x)-s^{*}(\ell )}= \frac{p^{*}(t;y,x)}{s^{*}(x)-s^{*}(\ell )}{\mathrm {d}}t. \end{aligned}$$

(3.11)

From (3.6) and (3.11), $\mathbb{P}_{y}[\lambda _{x}\in {\mathrm {d}}t,\lambda _{x}>0, T_{\ell }< T_{r}]= \frac{p(t;y,x)}{s(x)-s(\ell )}{\mathrm {d}}t \mbox{ for } y< x$.  □

As discussed in Sect. 2.2, for the leverage process, we are interested in the last passage time of a Brownian motion (starting at $y$) with drift $\mu (\neq 0)$ and unit variance parameter to the state $\alpha$, i.e., $\lambda _{\alpha }=\sup \{t\ge 0: X_{t}=\alpha \}$. The scale function$s(\cdot )$ and the speed measure$m(\cdot )$ for such a Brownian motion are given by

$$ s(x)=\frac{1}{2\mu }(1-e^{-2\mu x}), \qquad m({\mathrm {d}}x)=2e^{2\mu x}{ \mathrm {d}}x $$

(3.12)

for $x\in (c,\infty )$, which is the state space in our case (Borodin and Salminen [3, Appendix 1]). The left boundary is attracting since $s(c)>-\infty$. The right boundary can be attracting ($s(\infty )<+\infty$ when $\mu >0$) or non-attracting ($s(\infty )=+\infty$ when $\mu <0$). We now apply Proposition 3.1 to our model (2.2) with (2.3).

Corollary 3.4

Let$X$be a Brownian motion with drift$\mu \neq 0$and unit variance parameter and let$c$be a regular killing boundary. For any$y,\alpha \in \mathcal{I}'$satisfying$\alpha \le y$, the distribution of$\lambda _{\alpha }$on the set$\{T_{c}<\infty \}$ (i.e., when the company becomes insolvent in finite time) is given by

$$ \mathbb{P}_{y}[\lambda _{\alpha }\in {\mathrm {d}}t,T_{c}< \infty ]= \frac{p(t; y, \alpha )}{\frac{1}{2\mu }(e^{-2\mu c}-e^{-2\mu \alpha })}{ \mathrm {d}}t, $$

(3.13)

where$p(t; u, v)$denotes the transition density, with respect to the speed measure$m({\mathrm {d}}v)=2e^{2\mu v}{\mathrm {d}}v$, of the Brownian motion$X$being killed at$c$, which is given by

$$ p(t; u, v)=\frac{1}{2\sqrt{2\pi t}}e^{-\mu (u+v)-\frac{\mu ^{2}t}{2}} \big(e^{-\frac{(u-v)^{2}}{2t}}-e^{-\frac{(u+v-2c)^{2}}{2t}}\big) $$

(3.14)

for$u,v>c$. For$\alpha >y$, the distribution of$\lambda _{\alpha }$on the set$\{T_{c}<\infty \}$has an atom at 0. The continuous part$\mathbb{P}_{y}[\lambda _{\alpha }\in {\mathrm {d}}t,\lambda _{\alpha }>0,T_{c}< \infty ]$is given by (3.13).

Proof

The case $\mu <0$ corresponds to Case 1 and $\mu >0$ corresponds to Case 2. We simply use the proof of Proposition 3.1 with $\ell =c$. □

Remark 3.5

(1) Equation (3.14) is equation $(2.1.8)$ in Baldeaux and Platen [1, Corollary 2.1.10], where $u,v>c$.

(2) When $\mu >0$, we have $s(r)=s(\infty )=\frac{1}{2\mu }$ and the company does not become insolvent in finite time with probability $\mathbb{P}_{y}[T_{r}< T_{c}]=1-e^{-2\mu (y-c)}$.

3.2 Time until killing after last passage time

We want to find $\mathbb{P}_{y}[T_{\ell }-\lambda _{\alpha }\in {\mathrm {d}}t, T_{\ell }< \infty ]$. However, since $T_{\ell }$ and $\lambda _{\alpha }$ are not independent under $\mathbb{P}_{y}$, it is not easy to compute this distribution. To overcome this difficulty, we consider the reversed path of the conditioned diffusion $X^{*}$ (introduced in the proof of Proposition 3.1) from $\ell$ and its first passage time to $\alpha$. While the first passage time distribution is perhaps not always available, it is much more convenient than handling the joint density of $\lambda _{\alpha }$ and $T_{\ell }$ in the original problem. Note that $X^{*}$ hits the state $\ell$ a.s. and is killed at $\ell$. The task is to identify the reverse process of $X^{*}$. We refer the reader to Chung and Walsh [4, Sect. 13.9] for results regarding reversal from a random time.

In this section, it is convenient to use for the original diffusion $X$ the representation $X=\{\omega (t), t\ge 0, \mathbb{P}_{y}\}$. Then we can denote our transformed diffusions by modifying the time period to be considered and the probability law. This notation is in line with Salminen [27].

Proposition 3.6

Let$X$be a general diffusion process as in Sect. 2, starting from$y \in \mathcal{I}$. Assume that$\ell$is a regular or exit boundary and consider the diffusion$X^{*}$ ($X$ conditioned to hit$\ell$in finite time). Then in Case 1 and Case 2, the reversed process of$X^{*}$is its$k_{r}$-transform starting from$\ell$ (its entrance boundary) and killed at its last passage time to$y$. That is, the two processes$\{\omega ({T_{\ell }-t}), 0< t< T_{\ell }, \mathbb{P}_{y}^{*}\}$and$\{\omega (t), 0< t< \lambda _{y},(\mathbb{P}_{\ell }^{*})^{k_{r}} \}$have the same law.

Proof

We confirm that the $k_{r}$-transform of $X^{*}$, starting at $\ell$ and reversed at its last passage time to $y$, is indeed the original $X^{*}$. From (3.7), we have $s^{*}(\ell )>-\infty$ and $s^{*}(r)=+\infty$ (recall Case 1). For simplicity, in this proof, we omit the superscript ^∗when referring to$X^{*}$or the functionals associated with$X^{*}$. From (3.9), we have $s^{r}(x)-s^{r}(\ell )=+\infty$ for $x\in \mathcal{I}$. Also,

$$\begin{aligned} &\int _{\ell }^{x}\big(s^{r}(x)-s^{r}(\eta )\big)m^{r}({\mathrm {d}}\eta ) \\ &=\int _{\ell }^{x}\left (\frac{1}{s(\eta )-s(\ell )}- \frac{1}{s(x)-s(\ell )}\right )\big(s(\eta )-s(\ell )\big)^{2}m({\mathrm {d}} \eta ) \\ &< \int _{\ell }^{x}\left (\frac{1}{s(\eta )-s(\ell )}\right )\big(s( \eta )-s(\ell )\big)^{2}m({\mathrm {d}}\eta ) \\ &=\int _{\ell }^{x}\big(s(\eta )-s(\ell )\big)m({\mathrm {d}}\eta )< \infty , \end{aligned}$$

where the last inequality holds due to $\ell$ being a regular or exit boundary for $X$. This proves that $\ell$ is an entrance boundary for the $k_{r}$-transform $X^{k_{r}}$ (Karlin and Taylor [17, Chap. 15, Table 6.2]). The Green function of $X^{k_{r}}$ is

$$G^r(y,z)=\{\begin{array}{cc}{s}^r(r)-s^r(z),& y\le z,\\ s^r(r)-s^r(y),& z\le y.\end{array}$$

(3.15)

Recall that as in Chung and Walsh [4, Definition 11.23], a random variable $L$ with values in $[0, \infty ]$ is co-optional if for all $t\ge 0$, we have $L\circ \theta (t)=(L-t)^{+}$, where $\theta (t)$ is the shift operator. Recall that Nagasawa’s theorem on time reversal in this context reads as follows; see Nagasawa [24] and Sharpe [29].

Theorem 3.7

Let$X$and$\widehat{X}$be standard Markov processes in duality relative to a$\sigma$-finite reference measure$\xi$on their common state space$E$. Let$u(x, y)$be the potential kernel density relative to$\xi$so that

$$ Uf(x)=\mathbb{E}_{x}\bigg[\int _{0}^{\infty }f(X_{t}){\mathrm {d}}t\bigg]= \int _{E} u(x, y) f(y)\xi ({\mathrm {d}}y). $$

Let$L$be a co-optional time for$X$. Denote$\widetilde{X}$by

$$\begin{aligned} \widetilde{X}_{t}:=\left \{ \textstyle\begin{array}{llll} X_{(L-t)-} &\quad \textit{for } 0< t< L \; \textit{on} \; \{0< L< \infty \}, \\ \Delta & \quad \textit{otherwise}. \end{array}\displaystyle \right . \end{aligned}$$

For an initial distribution$\lambda$, let$v(y):=\int _{E} \lambda ({\mathrm {d}}x)u(x, y)$. Then under$\mathbb{P}_{\lambda }$, the reversed process$(\widetilde{X}_{t})_{t>0}$is a homogeneous Markov process on$E$with transition semigroup$(\widetilde{P}_{t})$given by

$$\begin{aligned} \widetilde{P}_{t} f(y)=\left \{ \textstyle\begin{array}{llll} \widehat{P}_{t}(fv)(y)/v(y), & \quad 0< v(y)< \infty , \\ 0, & \quad \textit{otherwise}. \end{array}\displaystyle \right . \end{aligned}$$

In our case, $X^{k_{r}}$ is self-dual relative to its speed measure $m^{r}$. Set $\lambda ({\mathrm {d}}x)=\delta _{\ell }({\mathrm {d}}x)$, the Dirac measure at $\ell$, and use Theorem 3.7 with $E=[\ell ,r)$, $\xi ({\mathrm {d}}y)=m^{r}({\mathrm {d}}y)$, $L=\lambda _{y}^{r}$ (the last passage time of $X^{k_{r}}$ to $y$), $u(x,y)=G^{r}(x,y)$ to obtain

$$ v^{r}(z)=\int _{\ell }^{r} \delta _{\ell }({\mathrm {d}}y)G^{r}(y, z)=G^{r}( \ell , z)=s^{r}(r)-s^{r}(z), $$

where we use the first case of (3.15) since $\ell$ is the lower boundary of the state space. For a nonnegative Borel-measurable function $f$, the potential operator of $\widetilde{X^{k_{r}}}$ (the reversed process of $X^{k_{r}}$), denoted by $V$, is written as

$$\begin{aligned} Vf(y)&=\frac{U(fv^{r})(y)}{v^{r}(y)}=\int _{\ell }^{r} G^{r}(y,z) \frac{v^{r}(z)}{v^{r}(y)}f(z)m^{r}({\mathrm {d}}z) \\ &=\int _{\ell }^{y} \big(s^{r}(r)-s^{r}(y)\big) \frac{s^{r}(r)-s^{r}(z)}{s^{r}(r)-s^{r}(y)}f(z)m^{r}({\mathrm {d}}z) \\ &\phantom{=:}+\int _{y}^{r} \frac{(s^{r}(r)-s^{r}(z))^{2}}{s^{r}(r)-s^{r}(y)}f(z)m^{r}({ \mathrm {d}}z) \\ &=\int _{\ell }^{r} G^{**}(y, z)f(z)\big(s^{r}(r)-s^{r}(z)\big)^{2}m^{r}({ \mathrm {d}}z), \end{aligned}$$

where

$$G^{\ast \ast }(y,z):=\{\begin{array}{cc}\frac{1}{s^r(r)-s^r(z)},& z\le y,\\ \frac{1}{s^r(r)-s^r(y)},& y\le z.\end{array}$$

By (3.9), we have $s^{r}(r)=0$ and $Vf(y)$ is simplified to

$$ Vf(y)=\int _{\ell }^{r} \bigg(\Big(-\frac{1}{s^{r}(z)}\Big)\wedge \Big(-\frac{1}{s^{r}(y)}\Big)\bigg)f(z)\big(s^{r}(z)\big)^{2}m^{r}({ \mathrm {d}}z). $$

(3.16)

This reversed transform $\widetilde{X^{k_{r}}}$ dies only at $\ell$. Below we use $\widetilde{\mathbb{E}^{r}}$ to denote the law of $\widetilde{X^{k_{r}}}$. Take any $\ell < y< a< b< r$. Using the strong Markov property, we have

Hence from (3.16) and (3.9), because $\ell < y< a$ and $s^{r}(\cdot )$ is monotone increasing. This shows that the scale function of $\widetilde{X^{k_{r}}}$ coincides with that of $X$. Also, $(s^{r}(z))^{2}m^{r}({\mathrm {d}}z)$ becomes the speed measure of $\widetilde{X^{k_{r}}}$ by definition and also coincides with the speed measure of $X$.

Since both $X^{*}$ (which has been denoted by $X$ in this proof) and $\widetilde{(X^{*})^{k_{r}}}$ are killed only at $\ell$ and their scale functions and speed measures coincide, we conclude that the reversed process from $\ell$ of the diffusion $X^{*}$ is its $k_{r}$-transform starting from $\ell$ and killed at its last passage time to $y$.  □

We want to find $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha }\in {\mathrm {d}}t, T_{c}<\infty ]$ for $\alpha ,y\in \mathcal{I}'$ for the leverage process in Sect. 2.2. This distribution should be useful in knowing how long the firm would have for implementing its measures to avoid insolvency. Note that for risk management purposes, we are interested in the case when $\alpha \le y$. In Corollary 3.8, we identify the reversed process of our model (2.2), and in Proposition 3.9, we provide a semi-explicit form of the density of the time left until killing after $\lambda _{\alpha }$ in terms of its Laplace transform. See Remark 3.10 for the case when $\alpha >y$.

Corollary 3.8

Let$X=\{\omega (t),0\le t< T_{c},\mathbb{P}_{y}\}$be a Brownian motion with drift$\mu \neq 0$and unit variance on$\mathcal{I}'=(c,\infty )$, with$c$being a regular killing boundary.

(a) When$\mu <0$, the reversed process$\tilde{X}=\{\omega (T_{c}-t),0< t< T_{c},\mathbb{P}_{y}\}$of$X$has the generator$\tilde{\mathfrak{G}}$given by

$$ \tilde{\mathfrak{G}}f(x)=\mu \coth \big(\mu (x-c)\big)f'(x)+ \frac{1}{2}f''(x), $$

(3.17)

and with respect to its speed measure$\tilde{m}({\mathrm {d}}v)= \frac{(e^{-2\mu c}-e^{-2\mu v})^{2}e^{2\mu v}{\mathrm {d}}v}{2\mu ^{2}}$, the transition density of$\tilde{X}$is given by

$$ \tilde{p}(t; u, v)= \frac{e^{-\mu (u+v)-\frac{\mu ^{2}t}{2}} (e^{-\frac{(u-v)^{2}}{2t}}-e^{-\frac{(u+v-2c)^{2}}{2t}})}{2\sqrt{2\pi t}(\frac{1}{2\mu })^{2}(e^{-2\mu c}-e^{-2\mu v})(e^{-2\mu c}-e^{-2\mu u})} $$

for$u,v>c$and

$$ \tilde{p}(t; c, v)=\frac{2\mu (v-c)}{t\sqrt{2\pi t}} \frac{e^{-\frac{(v-c)^{2}}{2t}-\mu (v-c)-\frac{\mu ^{2}t}{2}}}{e^{-2\mu c}-e^{-2\mu v}} $$

for$u=c$. For$c<\alpha \le y<\infty$, the distribution of$T_{c}-\lambda _{\alpha }$under$\mathbb{P}_{y}$is the same as that of$T_{\alpha }$under$\tilde{\mathbb{P}}_{c}$, where$\tilde{\mathbb{P}}$denotes the probability law of$\tilde{X}$.

(b) When$\mu >0$, $X$conditioned to hit$c$in finite time (denoted by$X^{*}$) is a Brownian motion with negative drift$-\mu$and unit variance, killed at$c$. Its reversed process$\widetilde{X^{*}}=\{\omega (T_{c}-t),0< t< T_{c},\mathbb{P}_{y}^{*}\}$has the generator in (3.17), and its speed measure and transition density have the same form as in (a) with$\mu$replaced by$-\mu$. For$c<\alpha \le y<\infty$, we have the distribution

$$ \mathbb{P}_{y}[T_{c}-\lambda _{\alpha }\in {\mathrm {d}}t, T_{c}< \infty ]= \widetilde{\mathbb{P}^{*}_{c}}[T_{\alpha }\in {\mathrm {d}}t]\mathbb{P}_{y}[T_{c}< \infty ], $$

where$\widetilde{\mathbb{P}^{*}}$denotes the probability law of$\widetilde{X^{*}}$.

Proof

(a) Using Proposition 3.6, $X^{*}$ is the original diffusion $X$ and we are interested in finding $X^{k_{r}}$ which is the reversed process $\tilde{X}$. Let $\tilde{\mathbb{P}}$ denote the probability law of $\tilde{X}$. From (3.9), we obtain with (3.12) that

$$\begin{aligned} s^{r}(x)&=-\frac{1}{\frac{1}{2\mu }(e^{-2\mu c}-e^{-2\mu x})}, \\ m^{r}({\mathrm {d}}x)&=\bigg(\frac{1}{2\mu }(e^{-2\mu c}-e^{-2\mu x})\bigg)^{2}2e^{2 \mu x}{\mathrm {d}}x =:\bar{m}^{r}(x) {\mathrm {d}}x. \end{aligned}$$

Since $\tilde{\mathfrak{G}} f(x)=\frac{1}{\bar{m}^{r}(x)} \frac{{\mathrm {d}}}{{\mathrm {d}}x}(\frac{1}{(s^{r}(x))'} \frac{{\mathrm {d}}f(x)}{{\mathrm {d}}x})$ (see e.g. Karlin and Taylor [17, Chap. 15, Sect. 3]), we use $s^{r}(\cdot )$ and $\bar{m}^{r}(\cdot )$ to obtain (3.17). The transition density with respect to the speed measure is obtained by (3.10) and (3.14). The entrance law from $c$ is due to L’Hôpital’s rule, and $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha }\in {\mathrm {d}}t\vert T_{c}< \infty ]=\tilde{\mathbb{P}}_{c}[T_{\alpha }\in {\mathrm {d}}t, T_{\alpha }< \lambda _{y}]$ by Proposition 3.6. When $\alpha \le y$, we have $\tilde{\mathbb{P}}_{c}[T_{\alpha }\in {\mathrm {d}}t,T_{\alpha }<\lambda _{y}]= \tilde{\mathbb{P}}_{c}[T_{\alpha }\in {\mathrm {d}}t]$ and obtain the final assertion.

(b) By direct computation using (3.7), (3.8), (3.12), and (3.14), we confirm that the probability law of $X^{*}$, $\mathbb{P}_{y}^{*}[X_{t}\in {\mathrm {d}}x]$ with $x,y>c$, coincides with that of a Brownian motion with negative drift $-\mu$ and unit variance, killed at $c$. Hence all the results presented in (a) apply to $X^{*}$ with $\mu$ replaced by $-\mu$. □

Proposition 3.9

Let$\alpha$$\le y$for any$y,\alpha \in \mathcal{I}'$. Given$T_{c}<\infty$, the time until the killing at state$c$after$\lambda _{\alpha }$for a Brownian motion with drift$\mu \neq 0$and unit variance is given by

$$ \mathbb{P}_{y}[T_{c}-\lambda _{\alpha }\in {\mathrm {d}}t\lvert T_{c}< \infty ]=\lim _{x\downarrow c} \frac{\sinh (\mu (\alpha -c))}{\sinh (\mu (x-c))} e^{-\frac{1}{2}\mu ^{2} t}\mathbb{P}_{x}[T_{\alpha }^{B}\in {\mathrm {d}}t, t< T_{c}^{B}], $$

(3.18)

where$B=(B_{t})_{t\ge 0}$is a Brownian motion with zero drift and unit variance starting at$x$under$\mathbb{P}_{x}$and$T_{\alpha }^{B}:=\inf \{t\ge 0: B_{t}=\alpha \}$. With$q>0$, $\mathbb{P}_{x}[T_{\alpha }^{B}\in {\mathrm {d}}t, t< T_{c}^{B}]$has the Laplace transform

$$ \int _{0}^{\infty }e^{-qt}\mathbb{P}_{x}[T_{\alpha }^{B}\in {\mathrm {d}}t, t< T_{c}^{B}]= \frac{\sinh (\sqrt{2q}(x-c))}{\sinh (\sqrt{2q}(\alpha -c))} $$

(3.19)

and it holds that

$$ \mathbb{E}_{y}[e^{-q(T_{c}-\lambda _{\alpha })}\lvert T_{c}< \infty ]= \frac{\sqrt{2q+\mu ^{2}}}{\mu } \frac{\sinh (\mu (\alpha -c))}{\sinh (\sqrt{2q+\mu ^{2}}(\alpha -c))}. $$

(3.20)

Proof

Due to the results of Corollary 3.8, the problem reduces to finding the distribution of the first passage time of the reversed diffusion (starting at $c$) of a Brownian motion with drift $-|\mu |$ and unit variance (defined in Corollary 3.8). Let us denote this reversed diffusion by $Y$. By (3.17), $Y$ has the drift $\mu \coth (\mu (x-c))$, taking values in $\mathbb{R}_{+}$ for any $\mu \in \mathbb{R}\backslash \{0\}$ and $x>c$. For notational simplicity, we use ℙ and $\mathbb{E}$ to denote the probability law and expectation associated with $Y$, respectively.

Given any small $\varepsilon >0$, we consider another Brownian motion $B=(B_{t})_{t\ge 0}$ with zero drift and unit variance on some probability space $(\Omega , \mathcal{F},\mathbb{P})$ with the filtration $\mathbb{F}=(\mathcal{F}_{t})_{t\ge 0}$ and such that $B_{0}=x$ a.s. with $x\in (c+\varepsilon ,\alpha )$. This can be the original probability space defined in Sect. 2. Therefore, we use the same notation. We let $T_{z}^{B}=\inf \{t\ge 0: B_{t}=z\}$ denote the hitting time of $z\in \mathbb{R}$ for $B$. We set for $t\in \mathbb{R}_{+}$

The integrand is bounded for $s\ge 0$, taking values in $[\mu \coth (\mu (\alpha +1-c)),\mu \coth (\mu \varepsilon )]$, and by Karatzas and Shreve [16, Proposition 3.5.12 and its preceding argument], $(Z_{t})_{t \geq 0 }$ is a martingale under ℙ and in ${\mathbb{F}}$. Itô’s formula applied to the function $\ln (\sinh (|\mu |z))$ with $z\in (0,\infty )$ yields

$$\begin{aligned} &\ln \Big(\sinh \big(|\mu |(B_{t\wedge T_{c+\varepsilon }^{B}\wedge T_{ \alpha +1}^{B}}-c)\big)\Big)-\ln \Big(\sinh \big(|\mu |\left (x-c \right )\big)\Big) \\ &= \int _{0}^{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}} \mu \coth \big(\mu (B_{s}-c)\big){\mathrm {d}}B_{s} \\ &\phantom{=:}+\frac{1}{2}\int _{0}^{t\wedge T_{c+\varepsilon }^{B}\wedge T_{ \alpha +1}^{B}}\mu ^{2}\Big(1-\coth ^{2}\big(\mu (B_{s}-c)\big)\Big){ \mathrm {d}}s \qquad \text{$\mathbb{P}_{x}$-a.s.}, \end{aligned}$$

resulting in

$$ \frac{\sinh (\mu (B_{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}-c))}{\sinh (\mu (x-c))}e^{- \frac{1}{2}\mu ^{2} (t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B} )}=Z_{t} \qquad \mathbb{P}_{x}\mbox{-a.s.} $$

(3.21)

Hence $0\le Z_{t}\le \frac{\sinh (\mu (\alpha +1-c))}{\sinh (\mu (x-c))}$ for $t \geq 0$ and $(Z_{t})$ is a nonnegative uniformly integrable family of random variables. By Karatzas and Shreve [16, Problem 1.3.20], $Z_{\infty }:=\lim _{t\to \infty }Z_{t}$ exists ℙ-a.s. and $(Z_{t})_{0\leq t \leq \infty }$ is a martingale for $(\mathcal{F}_{t})_{0\leq t \leq \infty }$ with $\mathcal{F}_{ \infty }=\bigvee _{t \geq 0}\mathcal{F}_{t}$. Note that (see Chung and Williams [5, Eq. (6.7)]). Moreover, $Z_{\infty }=Z_{T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}$ ℙ-a.s. and

Define a new probability measure $\hat{\mathbb{P}}$ on $(\Omega ,\mathcal{F})$ by the Radon–Nikodým density $Z_{\infty }$, that is,

$$ \frac{{\mathrm {d}}\hat{\mathbb{P}}}{{\mathrm {d}}\mathbb{P}}=Z_{\infty }. $$

Since $Z_{\infty }>0$ ℙ-a.s., $\hat{\mathbb{P}}$ is equivalent to ℙ. By noting that $T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}<\infty$ a.s. and using Karatzas and Shreve [16, Theorem 3.5.1],

$$ \bigg(B_{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}- \int _{0}^{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}} \mu \coth \big(\mu (B_{s}-c)\big){\mathrm {d}}s\bigg)_{0 \leq t \leq T_{c+ \varepsilon }^{B}\wedge T_{\alpha +1}^{B}} $$

under $\hat{\mathbb{P}}$ has the same law as a Brownian motion with zero drift and unit variance, starting at $x$ a.s. By writing

$$\begin{aligned} B_{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}&=\bigg(B_{t \wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}-\int _{0}^{t \wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}}\mu \coth \big( \mu (B_{s}-c)\big){\mathrm {d}}s\bigg) \\ &\phantom{=:}+\int _{0}^{t\wedge T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}} \mu \coth \big(\mu (B_{s}-c)\big){\mathrm {d}}s, \end{aligned}$$

we see that $(B_{t})$ has for $t\in [0,T_{c+\varepsilon }^{B}\wedge T_{\alpha +1}^{B}]$ the same probability law under $\hat{\mathbb{P}}_{x}$ as $(Y_{t})$ for $t\in [0, T^{Y}_{c+\varepsilon }\wedge T^{Y}_{\alpha +1}]$ under $\mathbb{P}_{x}$. Here $T^{Y}$ denotes the hitting time of $Y$. Therefore, since $T_{\alpha }^{B}< T_{\alpha +1}^{B}$$\hat{\mathbb{P}}_{x}$-a.s. and $T^{Y}_{\alpha }< T^{Y}_{\alpha +1}$$\mathbb{P}_{x}$-a.s.,

$$ \tilde{H}_{\alpha }^{\varepsilon }:=\inf \{u\ge 0: Y_{u\wedge T^{Y}_{c+ \varepsilon }}=\alpha \} \qquad \mbox{under } \mathbb{P}_{x} $$

has the same distribution as

$$ H_{\alpha }^{\varepsilon }:=\inf \{u\ge 0: B_{u\wedge T_{c+ \varepsilon }^{B}}=\alpha \} \qquad \mbox{under } \hat{\mathbb{P}}_{x}. $$

So we obtain

where we used the martingale property of $Z$ in the fourth equality and optional sampling for the uniformly integrable martingale $Z$ in the last equality. From (3.21),

Thus we obtain

By letting $\varepsilon \downarrow 0$ and setting $\tilde{H}_{ \alpha }:=\inf \{u\ge 0: Y_{u\wedge T^{Y}_{c}}=\alpha \}=\inf \{u\ge 0: Y_{u}=\alpha \}$ ($c$ is the entrance boundary for $Y$ as proved in Proposition 3.6), we have

where we used monotone convergence for the final equality. This leads to the density

$$\begin{aligned} \mathbb{P}_{x} [\tilde{H}_{\alpha }\in {\mathrm {d}}u ]&= \frac{\sinh (\mu (\alpha -c))}{\sinh (\mu (x-c))}e^{-\frac{1}{2}\mu ^{2} u}\mathbb{P}_{x} [T_{\alpha }^{B}\in {\mathrm {d}}u,u< T_{c}^{B} ], \end{aligned}$$

where $\mathbb{P}_{x}[T_{\alpha }^{B}\in {\mathrm {d}}u,u< T_{c}^{B}]$ has the Laplace transform (3.19) (see Kyprianou [19, Sect. 8.2] and Borodin and Salminen [3, Part II, Sect. 1.3]). Hence we obtain (3.18). Using (3.19), we have for $q>0$ that

$$\begin{aligned} \mathbb{E}_{c} [e^{-q \tilde{H}_{\alpha }} ]&=\lim _{x\downarrow c} \mathbb{E}_{x} [e^{-q \tilde{H}_{\alpha }} ] \\ &=\lim _{x\downarrow c}\int _{0}^{\infty }e^{-qu}e^{-\frac{1}{2}\mu ^{2} u}\frac{\sinh (\mu (\alpha -c))}{\sinh (\mu (x-c))}\mathbb{P}_{x} [T_{ \alpha }^{B}\in {\mathrm {d}}u,u< T_{c}^{B} ] \\ &=\lim _{x\downarrow c} \frac{\sinh (\mu (\alpha -c))}{\sinh (\mu (x-c))} \frac{\sinh (\sqrt{2q+\mu ^{2}}(x-c))}{\sinh (\sqrt{2q+\mu ^{2}}(\alpha -c))} \\ &= \frac{\sqrt{2q+\mu ^{2}}\sinh (\mu (\alpha -c))}{\mu \sinh (\sqrt{2q+\mu ^{2}}(\alpha -c))}, \end{aligned}$$

where we evaluated the limit in the final equality after using L’Hôpital’s rule. This completes the proof of (3.20). □

Remark 3.10

Let $\tilde{\mathbb{P}}$ denote the probability law of the reversed process (defined in Corollary 3.8) of a Brownian motion with drift $-|\mu |\neq 0$ and unit variance, killed at $c$. When $c< y<\alpha <\infty$, we have $\tilde{\mathbb{P}}_{c}[T_{\alpha }\in {\mathrm {d}}t,T_{\alpha }<\lambda _{y}] \neq \tilde{\mathbb{P}}_{c}[T_{\alpha }\in {\mathrm {d}}t]$. The computation of the probability on the left-hand side requires the joint density of the hitting time and the last passage time.

3.3 Endogenising the threshold

In the previous sections, we calculated some functionals that involve $\lambda _{\alpha }$, the last visit to state $\alpha$ before the original process is killed. In this section, we wish to make the level $\alpha$ endogenous: we obtain this threshold as a solution to a certain appropriate optimisation problem. Let us consider again a general diffusion $X$ as in Sect. 2. To form an optimisation problem, it should be reasonable to assume the following:

(1) If the level of $\alpha$ is too low, $X$ may hit $\ell$ shortly after it is below $\alpha$. From the perspective of risk management, this means that the firm may become insolvent shortly after it finds itself below the precautionary threshold. In this case, the management has missed out on a bad sign on a timely basis. Hence, the management wants an alarm early enough to implement some measures.

(2) The company as a whole wants to minimise the time spent below a precautionary threshold. That time is given by . The creditors naturally want the company to operate above the threshold $\alpha$. From the shareholders’ point of view as well, the value of the investment in the company has decreased and they are at risk of losing the whole investment while the firm is operating below the level $\alpha$. Also, it will be harder to receive dividends.

For (1), we consider for fixed $t$ with $Q_{t}:=\sup \{s< t: X_{s}=\alpha \}$ the quantity

$$ \mathbb{P}_{y}\left [Q_{t}=\lambda _{\alpha }, X_{t}\in (\ell , \alpha ) \right ]=\int _{\ell }^{\alpha } \frac{s(\alpha )-s(z)}{s(\alpha )-s(\ell )}\mathbb{P}_{y}[X_{t}\in { \mathrm {d}}z] $$

(3.22)

(see Sects. 4.1.1 and 4.1.2). The equality holds due to the strong Markov property. This quantity can be computed by using the first case of the representation of $\mathbb{P}_{y}[\lambda _{x}>t |\mathcal{F}_{t}]$ in Remark 3.2 (by replacing $x$ there with $\alpha$). The probability in (3.22) indicates how likely it is that when the process is below $\alpha$ at time $t$, it will never recover to $\alpha$ and will hit the killing boundary. This quantity is an increasing function of $\alpha$. The firm can be sufficiently cautious by setting the alarming $\alpha$ at a high level (thus raising the probability in (3.22)), but the time spent below $\alpha$ (discussed in (2)) would be larger. In particular, for (2), we can consider for $q > 0$ the Laplace transform

where the last equality holds due to the dominated convergence theorem. If we increase $\alpha$ (by setting $\alpha$ closer to $y$), the quantity $A_{\infty }$ increases (and hence $\mathbb{E}_{y}[e^{-q A_{\infty }}]$ decreases). Accordingly, for a given $t$, we set the optimisation problem as a convex combination of two terms via

(3.23)

where $\Gamma \in [0,1]$ indicates the relative importance between the two terms. Using $\Gamma$, one can adjust the priority of the two quantities in a flexible way (see Sect. 4.3). The first term indicates the probability that up to time $t$, the process $X$ is already killed, or otherwise $X_{t}$ is in $(\ell , \alpha )$ and does not return to the level $\alpha$. From the risk management’s point of view, we call the second term a financial distress. This term is constructed based on the fact that our primary interest lies in the case where $T_{\ell }< T_{r}$. This corresponds to killing (insolvency) occurring in finite time. For $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha }, X_{t}\in (\ell ,\alpha )]$, the inclusion of the event $T_{\ell }< T_{r}$ in this probability would not make any difference.

Equation (3.23) is constructed for a general diffusion $X$. We briefly summarise its implication for credit risk management. A lower $\alpha$ would decrease the time spent below the precautionary threshold $A_{\infty }$, increasing the second term. On the other hand, a low level of $\alpha$ is not appropriate as a precautionary threshold and would make the first term smaller. In summary, the management would want to set $\alpha$ to a level that would minimise the risk of insolvency; however, if $\alpha$ is too high, this would increase the time spent in financial distress. This is the kind of trade-off that we wanted to see.

Now, is evaluated as in Zhang [31, Sect. 4.1] with $b\uparrow r$ and $a\downarrow \ell$ there as

The quantity $W_{q,1}(\alpha ,\ell )$ is defined in Zhang [31, Sect. 2] in the following manner. Let $\varphi$ and $\psi$ denote the positive increasing and decreasing solutions of the ordinary differential equation $\mathfrak{G}f(x)=qf(x)$ for $q>0$, where $\mathfrak{G}$ is the generator of $X$. There exists a constant $\omega _{q}>0$ satisfying $\omega _{q} s'(x)=\varphi '(x)\psi (x)-\psi '(x)\varphi (x)$. Setting

$$W_q(x,y)={\omega }_q^{-1}det\left(\begin{array}{cc}\phi (x)& \phi (y)\\ \psi (x)& \psi (y)\end{array}\right)$$

for $x,y\in \mathcal{I}$, we have $W_{q,1}(x,y)=\frac{\partial }{\partial x}W_{q}(x,y)$. Thus our optimisation problem becomes

$$\begin{aligned} v(y; t):=&\max _{\alpha \in [\ell , y]}\bigg(\Gamma \Big(\int _{\ell }^{ \alpha }\frac{s(\alpha )-s(z)}{s(\alpha )-s(\ell )}\mathbb{P}_{y}[X_{t} \in {\mathrm {d}}z]+\int _{0}^{t}\mathbb{P}_{y}[T_{\ell }\in {\mathrm {d}}z] \Big) \\ &\qquad \qquad +(1-\Gamma ) \frac{(s(r)-s(y))s'(\alpha )}{(s(r)-s(\alpha ))W_{q,1}(\alpha ,\ell )+s'(\alpha )W_{q}(\alpha ,\ell )} \bigg) \end{aligned}$$

(3.24)

for $s(r)<\infty$, and

$$\begin{aligned} v(y; t)&:=\max _{\alpha \in [\ell , y]}\bigg(\Gamma \Big(\int _{\ell }^{ \alpha }\frac{s(\alpha )-s(z)}{s(\alpha )-s(\ell )}\mathbb{P}_{y}[X_{t} \in {\mathrm {d}}z]+\int _{0}^{t}\mathbb{P}_{y}[T_{\ell }\in {\mathrm {d}}z] \Big) \\ &\phantom{=:}\qquad \qquad \,\,+(1-\Gamma ) \frac{s'(\alpha )}{W_{q,1}(\alpha ,\ell )}\bigg) \end{aligned}$$

(3.25)

for $s(r)=\infty$.

Remark 3.11

Our formulation here is just an example of how $\alpha$ can be chosen for credit risk management. It is up to the party of interest (the management) to decide which quantities to use for representing trade-offs. Another quantity of interest can be $\int _{0}^{t} \mathbb{P}_{y}[\lambda _{\alpha }\in {\mathrm {d}}s]$ for a fixed $t$ and $\alpha \le y$ from Sect. 3.1. The quantity $\mathbb{P}_{y}[\lambda _{\alpha }\in {\mathrm {d}}t]$ decreases as $\alpha$ decreases (i.e., when $\alpha$ approaches $\ell$). This is easily checked if we consider $T_{\alpha }$ for the reversed process. We can also use the time left until killing after $\lambda _{\alpha }$ (see Propositions 3.6 and 3.9). The company management would want to make this quantity longer, since this would give them some time to recover.

When $X$ is a Brownian motion with drift $\mu$ and unit variance on $(c,\infty )$ with $c$ being a regular killing boundary, (3.24) and (3.25) become for $\mu >0$

$$\begin{aligned} &v(y; t) \\ &:=\max _{\alpha \in [c, y]}\bigg(\Gamma \Big(\int _{c}^{\alpha } \frac{e^{-2\mu z}-e^{-2\mu \alpha }}{e^{-2\mu c}-e^{-2\mu \alpha }} \frac{e^{-\mu (y-z)-\frac{\mu ^{2}t}{2}}}{\sqrt{2\pi t}}\big(e^{- \frac{(y-z)^{2}}{2t}}-e^{-\frac{(y+z-2c)^{2}}{2t}}\big){\mathrm {d}}z \\ &\qquad \qquad \qquad +\int _{0}^{t}\frac{|c-y|}{\sqrt{2\pi u^{3}}}e^{- \frac{(c-y-\mu u)^{2}}{2u}}{\mathrm {d}}u\Big) \\ &\qquad \qquad \qquad + \frac{(1-\Gamma )e^{\mu (\alpha +c)}e^{-2\mu y}}{\cosh (\sqrt{\mu ^{2}+2q}(\alpha -c))+\frac{\mu }{\sqrt{\mu ^{2}+2q}}\sinh (\sqrt{\mu ^{2}+2q}(\alpha -c))} \bigg), \end{aligned}$$

(3.26)

and for $\mu <0$

$$\begin{aligned} &v(y; t) \\ &:=\max _{\alpha \in [c, y]}\bigg(\Gamma \Big(\int _{c}^{\alpha } \frac{e^{-2\mu z}-e^{-2\mu \alpha }}{e^{-2\mu c}-e^{-2\mu \alpha }} \frac{e^{-\mu (y-z)-\frac{\mu ^{2}t}{2}}}{\sqrt{2\pi t}}\big(e^{- \frac{(y-z)^{2}}{2t}}-e^{-\frac{(y+z-2c)^{2}}{2t}}\big){\mathrm {d}}z \\ &\qquad \qquad \qquad +\int _{0}^{t}\frac{|c-y|}{\sqrt{2\pi u^{3}}}e^{- \frac{(c-y-\mu u)^{2}}{2u}}{\mathrm {d}}u\Big) \\ &\qquad \qquad \qquad + \frac{(1-\Gamma )e^{-\mu (\alpha -c)}}{\cosh (\sqrt{\mu ^{2}+2q}(\alpha -c))-\frac{\mu }{\sqrt{\mu ^{2}+2q}}\sinh (\sqrt{\mu ^{2}+2q}(\alpha -c))} \bigg). \end{aligned}$$

(3.27)

We used $p(t;\cdot , \cdot )$ in (3.14) and the hitting time density (see Karatzas and Shreve [16, Chap. 3, Sect. 3.5.C]). For the discount rate $q$, one could use the expected return on the company’s asset or the weighted average of cost of capital (WACC). In our examples in Sect. 4, we defined $q$ as WACC (see Appendix for the calculation method).

4 Application to the leverage process

4.1 Last passage time

Below, we illustrate how the last passage time can be useful for risk management. For the analysis, we choose American Apparel Inc., which filed for bankruptcy protection in October 2015 (see [10]). The method to choose an appropriate alarming threshold is discussed in Sect. 3.3. Here we use two alarming thresholds for the analysis, namely $R^{*}=\frac{1}{0.8}=1.25$ and $R^{*}=\frac{1}{0.6}\approx 1.67$. These are the levels of the leverage ratio when debt makes up $80\%$ and $60\%$ of assets, respectively.

As discussed in Sect. 2.2, the study of the leverage process can be reduced to the study of a Brownian motion with drift; therefore, the last passage time of the leverage ratio to $R^{*}$ is equivalent to the last passage time $\lambda _{\alpha }$ of a Brownian motion with drift $\mu$ to an appropriate $\alpha$. While $\lambda _{\alpha }$ is not a stopping time, the mathematical foundation provided in our paper enables us to calculate certain probabilities associated with $\lambda _{\alpha }$, based on the information of the current position of the leverage process and the information available up to the current time. As we show below, the probabilities associated with $\lambda _{\alpha }$ provide very useful information for risk management.

4.1.1 Methodology

In order to analyse the distribution of the last passage time to $R^{*}$, we estimate the necessary parameters $\nu$ and $\sigma$ of the leverage process by the method in Duan [6], Duan [7] and Lehar [20]. This is the estimation method used for structural credit risk models, and it assumes that the company equity is a European call option written on the company’s assets with a strike price equal to a certain level of debt (see Sect. 2.2). In Lehar [20], it is assumed that the debt process grows at the risk-free rate $r_{f}$, which we follow. To emphasise this point in this section, we use the risk-free rate $r_{f}$ as the constant growth rate of debt $r_{D}$ in Sect. 2.2. Let us take the example of December 2013 and demonstrate the estimation procedure that we use for each month in the first column of Table 1.

Table 1 American Apparel Inc. parameters (up to 4 decimal points). Standard errors are displayed in parentheses. $A_{0}$, $D_{0}$, $R_{0}$ are the values at the end of each indicated month. 1-year treasury yield curve rate observed at the end of each indicated month was used as $r_{f}$

(1) At the end of December 2013, the estimated drift and volatility parameters ($\nu$ and $\sigma$) of the company’s asset process $A$ are −0.5080 and 0.2974, respectively. These parameters were calculated by using the equity and debt data of the previous 6 months. We set the debt level $D$ as the sum of “revolving credit facilities and current”, “cash overdraft”, “current portion of long-term debt”, “subord. notes payable – related party”, and one-half of “total long term debt”, all taken from the company’s balance sheet (December 2013). We use daily data for our estimation. Using the quarterly balance sheets, we obtain daily debt values by interpolation. We use the 1-year treasury yield at the end of December 2013 as the risk-free rate $r_{f}$. We calculate the drift in (2.2) as $\mu =\frac{\nu -r_{f}}{\sigma }$.

(2) We compute the initial asset value $A_{0}$ (i.e., the value at the end of December 2013) from the Black–Scholes formula (see Lehar [20]) by using $\sigma$$(=0.2974)$, the equity value $E_{0}$ and debt level $D_{0}$ at the end of December 2013 via

$$ E_{0}=A_{0} \Phi (d_{0})-D_{0} \Phi (d_{0}-\sigma \sqrt{T}), \qquad \text{where } d_{0}= \frac{\ln (A_{0}/D_{0})+\frac{\sigma ^{2} T}{2}}{\sigma \sqrt{T}}. $$

We set $T=1$ following Lehar [20]; $\Phi$ is the standard normal distribution function.

(3) We set $B_{0}^{A}=0$ and compute $R_{0}$ as the ratio of $A_{0}$ and $D_{0}$ to obtain $R_{0}=1.8596$. We compute $y$, $\alpha$ and $c$ from $\frac{1}{\sigma }\ln \frac{R D_{0}}{A_{0}}$ by setting $R=R_{0}$, $R=R^{*}$ and $R=1$, respectively. Note that $y$ is equal to 0.

For each reference month in Table 1, we calculate the necessary parameters (expressed as yearly estimates) using the method described above. Note that $R_{0}$ in Table 1 is the value of $R$ at the end of each estimation period, which is equal to the starting value in an empirical analysis regarding $\lambda _{\alpha }$. We are interested in the following four topics:

– Starting at $y$, what is the probability that the last passage time will occur within one year when the insolvency occurs in finite time? This is expressed by the quantity $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$. Note that $T_{c}<\infty$ a.s. when $\mu <0$. Since the parameters change depending on the reference month (Table 1), this quantity changes according to the starting reference point as well. Naturally, a higher probability indicates a greater credit risk. Note that when $\alpha >y$, the process may never reach $\alpha$. For such situations, we have calculated $\mathbb{P}_{y}[\lambda _{\alpha }=0]$ as well.

– At any point in time, by varying $R^{*}$ and studying the last passage time to each level, one can obtain detailed information about the credit risk. We set one reference month as a starting point and by varying $R^{*}$ from 1.2 to 2.5, we calculate $\mathbb{P}_{y}[\lambda _{\alpha }\in [0,1]]$ for each corresponding $\alpha$. We emphasise that by varying $R^{*}$, only the corresponding $\alpha$ change.

– We analyse the relationship between $\lambda _{\alpha }$ and the default probability (DP). At each reference point, we calculate the probability of defaulting at the end of next year in Merton’s [22] model. For this, we simulate the asset path for 1 year using the estimated parameters and compare the debt $D_{0}e^{r_{f}}$ and the asset value at the end of 1 year. If the asset value is smaller than the debt, we consider it as default. We also calculate $\mathbb{P}_{y}[T_{c}<1]$ which is naturally higher than DP, since the latter only considers the final asset and debt values.

– Finally, we calculate $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t}\in (c,\alpha )]$ in (3.22) with $c=\ell$. This is the probability that at a fixed time $t$, if the leverage ratio is below $R^{*}$, it will never reach $R^{*}$ again. We use this quantity in our optimisation problem in Sect. 3.3 as well. For our analysis, we set $t=\frac{1}{4}$ and $t=\frac{1}{2}$, meaning that we are interested in the position after 3 and 6 months. Note that this probability may be small due to the fact that $\mathbb{P}_{y}[X_{t}\in (c,\alpha )]$ is small. This in turn may be the result of $\mathbb{P}_{y}[T_{c}< t]$ being high. Therefore, we calculate all three quantities together for the sake of comparison.

4.1.2 Evaluations

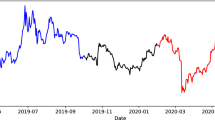
We discuss the four topics raised in Sect. 4.1.1 and demonstrate that we can extract more detailed information of credit conditions than when we only know $\mathbb{P}_{y}[T_{c}< t]$. For the two thresholds $R^{*}=1.25$ and $R^{*}=1.67$, Fig. 1 displays the probability $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$. This probability was calculated by applying Corollary 3.4 to the process in (2.2). We note that there is a sharp rise in the graph in 2013, which is consistent with the fact that American Apparel Inc. had problems with a new distribution center in 2013. For more details about the company’s financial situation before going bankrupt, see [15]. Although the company recovered to some extent during the period of June–December 2014, it went bankrupt in October 2015. The calculation results are summarised in Table 2 and we discuss them here.

Fig. 1

Last passage time to $R^{*}=1.25$ (black dotted line) and $R^{*}=1.67$ (red line) for American Apparel Inc. For $\alpha$ corresponding to $R^{*}$, the graph displays $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$ for Brownian motion with drift. In our setting, we have $y=0$. The estimated values are available in Table 2

Table 2 Calculation results (up to 4 decimal points) based on the parameters in Table 1. In our setting, we have $y=0$. Given the estimated parameters, by changing the level of $R^{*}$, only the corresponding values of $\alpha$ change, based on the equation $\alpha =\frac{1}{\sigma }\ln \frac{R^{*}D_{0}}{A_{0}}$ (see Sect. 2.2). For each starting point, DP denotes the probability of defaulting at the end of next year and $\Lambda _{\alpha }:=\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$

(1) The two quantities $\mathbb{P}_{y}[0 <\lambda _{\alpha } \leq 1, T_{c}<\infty ]$ and $\mathbb{P}_{y}[\lambda _{\alpha }=0]$ provide additional information to $\mathbb{P}_{y}[T_{c}<1]$ and the default probability (DP) regarding the creditworthiness of the company. For example, $\mathbb{P}_{y}[T_{c}<1]$ and DP are both high in Sep-13. Even though they decrease by more than $10\%$ in Dec-13, $\mathbb{P}_{y}[0< \lambda _{\alpha }\le 1, T_{c}<\infty ]$ still remains above $80\%$ for $R^{*}=1.67$. For the leverage ratio, this means that the probability of passing the level 1.67 last time within 1 year is more than $80\%$ and indicates a high credit risk.

(2) Moving to Mar-14, we see that $\mathbb{P}_{y}[\lambda _{\alpha }=0]$ has increased for $R^{*}=1.67$. Note that $R_{0}=1.4548<1.67$ for this reference month (see Table 1); therefore, there is around $44\%$ probability (see Table 2) that the firm will become insolvent before the leverage ratio recovers to 1.67. We also have a $90\%$ probability of passing the level 1.25 for the last time within 1 year. The drift $\mu$ turns positive for the next 3 reference points, but later becomes negative again.

(3) $\mathbb{P}_{y}[T_{c}<1]$ and DP greatly increase from Dec-14 to Mar-15, but the increase in $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$ is even greater for $R^{*}=1.67$ and signals increased risk. Finally, $R_{0}=1.5428<1.67$ in Jun-15 and $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$ becomes relatively small (see the red line in Fig. 1). However, this is because the probability of never recovering to 1.67 becomes $74\%$. This, together with all the other values, indicates an extremely high risk of insolvency. Note also that $\mathbb{P}_{y}[0<\lambda _{\alpha }\le 1, T_{c}<\infty ]$ is even higher in Jun-15 for the level $R^{*}=1.25$ (black dotted line), in contrast to $R^{*}=1.67$. It follows that by considering several levels of $R^{*}$, we can see the company’s credit conditions more closely. By reviewing these numbers, the management may fine-tune the company’s strategy, investment and operations.

The last passage time not only provides additional information to the default probability, but is also important in its own right. We illustrate this by looking into Table 3 and Fig. 2. Suppose that we are at the end of December 2013. The initial position of the leverage ratio is $R_{0}=1.8596$ for this point in time. We set various levels of $R^{*}$ (and hence $\alpha$) and compute $\mathbb{P}_{y}[0<\alpha \le 1]$, the probability that the premonition (i.e., the last passage to $R^{*}$) occurs within 1 year and $\mathbb{P}_{y}[\lambda _{\alpha }=0]$, the probability that the leverage ratio never hits $R^{*}$. Note that for this period, the drift of Brownian motion is $\mu =-1.7128$, and therefore $T_{c}<\infty$ a.s.

Fig. 2

Last passage time to varying $R^{*}$ for American Apparel Inc. by using the end of December 2013 as the starting point (see Tables 1 and 3). The horizontal axis displays $R^{*}$, and the vertical axis displays $\mathbb{P}_{y}[0<\alpha \le 1]$ (red lines) and $\mathbb{P}_{y}[\lambda _{\alpha }=0]$ (blue bars) for a Brownian motion with drift for the $\alpha$ corresponding to $R^{*}$. We recall that $R_{0}=1.8596$. Note that $y=0$ in our setting

Table 3 American Apparel Inc. last passage time probabilities (up to 4 decimal points) for varying $R^{*}$ by using the end of December 2013 as the starting point (see Table 1). We note that the change of $R^{*}$ affects only $\alpha$; all other parameters are unchanged. The dotted line between $R^{*}=1.9$ and $R^{*}=1.8$ indicates that $R_{0}=1.8596$ in December 2013 is located between the two numbers. Note that $y=0$ in our setting

(4) We see that there is more than $75\%$ probability that the leverage ratio will never recover to 2.1 or higher levels. Even though the current level is $R_{0}=1.8596$, this indicates that the levels above 2.1 are too high in credit quality relative to the company’s current position.

(5) Next, take $R^{*}=1.9$. Then $\mathbb{P}_{y}[\lambda _{\alpha }=0]$ is down to 0.2195, while the probability that the last passage to $R^{*}=1.9$ occurs within 1 year is 0.7045. These values together indicate that the probability of never recovering even to the level 1.9 after 1 year is more than $92\%$. This is valuable information because the decrease in the default probability from Sep-13 to Dec-13 and the increase in $\mu$ (Table 2) may be interpreted as credit quality improvement, while the information in Table 3 clearly indicates the presence of high risk and that the prognosis is not good.

(6) If we go further down to $R^{*}=1.5$, we have more than $75\%$ chance of passing the levels 1.5 and above for the last time within 1 year. Even for $R^{*}=1.2$, we have $\mathbb{P}_{y}[0<\alpha \le 1]=0.5347$. This means that there is about 50% chance that the company passes $R^{*}=1.2$ within 1 year and will not return to this level based on the current position of $R_{0}=1.8596$.

The quantities associated with the last passage time are more stable than the default probabilities; see points (1) and (5) above. These quantities should prevent the management from becoming too optimistic when the risk still persists. Finally, we calculate $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t}\in (c,\alpha )]$ (see (3.22)) which is the probability that at a fixed time $t$, if the leverage ratio is below $R^{*}$, it will never reach $R^{*}$ again. The results for $t=\frac{1}{4}$ and $t=\frac{1}{2}$ are displayed in Table 4 where we have chosen $\alpha$ corresponding to $R^{*}=1.67$.

Table 4 Summary of the results for $R^{*}=1.67$, with $\Theta _{\alpha }:=\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t} \in (c,\alpha )]$. In our setting, we have $y=0$

(7) At the end of September 2013, the probabilities of insolvency happening in 3 and 6 months are 0.13% and 9.34%, respectively. However, the probability that the leverage ratio never recovers to the level of 1.67 if it is below 1.67 after 3 (6) months is 30.88% (53.44%) and signals a high risk.

(8) The probability $\mathbb{P}_{y}[T_{c}< t]$ of becoming insolvent decreases in December 2013 for both $t=\frac{1}{4}$ and $t=\frac{1}{2}$. In contrast, we see an increase in the probability $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t}\in (c,\alpha )]$ which in turn indicates a still remaining high credit risk and provides valuable information to the management.

(9) At the end of March 2014, $\mathbb{P}_{y}[T_{c}< t]$ is more than 50% (70%) for $t=\frac{1}{4}$ ($t=\frac{1}{2}$); therefore, $\mathbb{P}_{y}[X_{t}\in (c,\alpha )]$ becomes smaller than the numbers in the previous data point Dec-13, which in turn decreases $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t}\in (c,\alpha )]$. For this reference point, $R_{0}=1.4548<1.67$ and the probability of never recovering to 1.67 is 43.53%, an increase from the previous data point (see Table 2).

(10) The situation worsens after December 2014. In June 2015, we observe $R_{0}=1.5428<1.67$ and there is roughly 13% probability of becoming insolvent within the next 3 months (see the last row in Table 4 with $t=1/4$). In addition to this, we find that there is 84% chance that the leverage ratio will be below 1.67 after 3 months, and when this is the case, it will never recover back to 1.67 with a probability of 80%. For $t=\frac{1}{2}$, $\mathbb{P}_{y}[T_{c}< t]$ is greater than 60%. Hence $\mathbb{P}_{y}[X_{t}\in (c,\alpha )]$ and $\mathbb{P}_{y}[Q_{t}=\lambda _{\alpha },X_{t}\in (c,\alpha )]$ are less than 40%. We also know that there is more than 74% chance that the leverage ratio never recovers to the level of 1.67 (see Table 2).

We should keep in mind that the occurrence of the last passage to $R^{*}$ within a certain period of time does not mean that insolvency occurs within that period. To obtain more information in this respect, we consider in the next section the time interval between the last passage time to a state and a subsequent insolvency.

4.2 Time left until insolvency after the last passage time

We use Proposition 3.9 to analyse the density $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha }\in {\mathrm {d}}t, T_{c}<\infty ]$. Figure 3 displays this density (black dashed line) for the reference point December 2013 (see Table 1) when $\alpha =-1.3358$, $c=-2.0862$ and $\mu =\frac{\nu -r_{f}}{\sigma }=-1.7128$ (taken from Table 2). This is the density of the time left until insolvency after the last passage time to $R^{*}=1.25$. We used Zakian’s method described in Halsted and Brown [13] to obtain the density. We numerically confirm that when taking the limit $x\to c$, the density in (3.18) converges. The distribution is concentrated in the range of $t\in [0.1, 0.2]$, so that insolvency is rather imminent after passing $\alpha =-1.3358$, since the company’s asset value has the negative drift parameter $\mu =-1.7128$. From the numerical result in Sect. 4.1.2, for $R^{*}=1.25$, the probability $\mathbb{P}_{y}[0<\alpha \le 1]$ is 0.5725 (see Table 2). Based on the analysis here, if the last passage time occurs, the time left for the management to improve credit quality is only a month or so.

Fig. 3

The density of the distribution $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha ^{*}}\in {\mathrm {d}}t, T_{c}< \infty ]$ for $\alpha ^{*}=-1.3358$ (black dashed line) and $\alpha ^{*}=-0.2334$ (red line) for American Apparel Inc. The end of December 2013 (see Tables 1 and 2) is used as the reference point. We have $y=0$, $c=-2.0862$, $\mu =-1.7128$

4.3 Endogenising the threshold

In this section, we solve the optimisation problem in Sect. 3.3 to endogeneously obtain the threshold $\alpha$ of interest for the leverage ratio. Figure 4 displays the optimal values of $\alpha$ (we call it $\alpha ^{*}$) for each $\Gamma$ by using the end of December 2013 as a reference point. As it is expected, when the second element of the objective function has priority (i.e., $\Gamma$ is small), the optimal $\alpha$ is low. This renders $A_{\infty }$ into a small value, making the Laplace transform greater. For $\Gamma \le 0.3$, we have a corner solution and $\alpha ^{*}=c$. In contrast, when the first element has priority (i.e., $\Gamma$ is large), the optimal $\alpha$ increases, giving a sense of danger as a precaution of potential threat even at high levels of $\alpha$. We remind the reader that $y=0$ in our setting; therefore, for large $\Gamma$, we have a corner solution and $\alpha ^{*}=y$. A closer look at Fig. 4 reveals that our optimisation problem has an inner solution for $\Gamma \in (0.32,0.46)$.

Fig. 4

Optimal values of $\alpha$ for $\Gamma \in [0,1]$ (left panel) and a closer look for $\Gamma \in [0.3,0.5]$ (right panel). The end of December 2013 (see Table 2) is chosen as a starting point. We have $y=0$, $c=-2.0862$, $\mu =-1.7128$, $q=0.2993$, $t=1$

4.4 Summary of the risk management tool

We summarise the proposed risk management tool in this paper. The management watches the company’s leverage ratio and they can estimate the drift and variance parameters of the firm’s asset value process, based on the method described in Sect. 4.1.1. Then for any future time horizon, the management can determine the threshold level $\alpha ^{*}$ below which the company should be operated on alert and with precaution. For this $\alpha ^{*}$, the management can compute $\mathbb{P}_{y}[\lambda _{\alpha ^{*}}\in {\mathrm {d}}t]$ (together with other associated probabilities in Sects. 4.1.1 and 4.1.2) and $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha ^{*}}\in {\mathrm {d}}t, T_{c}< \infty ]$ (as in Proposition 3.9) to make plans for future business operations. For example, suppose that the company has the parameters of December 2013 (see Table 1) and solves (3.27) with $\Gamma =0.4$ and $y=0$ to obtain the solution $\alpha ^{*}=-0.2334$. Then the red line in Fig. 3 is the density of the distribution $\mathbb{P}_{y}[T_{c}-\lambda _{\alpha ^{*}}\in {\mathrm {d}}t, T_{c}< \infty ]$ for $\alpha ^{*}=-0.2334$. This density is concentrated around 0.5 years. This means that if the management sets $\alpha$ as −0.2334, given the company’s current leverage level and asset growth rate, it is not unnatural to assume that there will be still half a year between the last passage to $\alpha$ and insolvency. The black dashed line is the density computed under the arbitrary assumption that $\alpha ^{*}=-1.3358$, which corresponds to debt being 80% of the assets. It is concentrated around 0.1–0.2 years. It follows that one could be better off by setting $\alpha ^{*}$ higher based on the optimisation of $\alpha$, rather than arbitrarily setting the level, to avoid further deterioration and to have a longer period until insolvency even after the last passage of $\alpha ^{*}$. Hence, together with $\mathbb{P}_{y}[\lambda _{\alpha ^{*}}\in {\mathrm {d}}t]$, one can extract information useful for risk management by the techniques presented in Sects. 3 and 4.

Remark 4.1

Finally, we comment on the possibility of extending our results in Sect. 3 to Lévy processes. Our analysis relies on the scale functions, speed measures and Green functions of diffusions. For spectrally negative Lévy processes, the scale function and the process conditioned to stay positive are well studied; see Kyprianou [19, Chap. 8], Kuznetsov et al. [18] and Bertoin [2, Chap. VII]. For the reversal of Lévy processes, it is well known that the dual of $X$, which is $-X$, has the same law as the reverse of $X$ from a fixed time (Bertoin [2, Lemma II.2]). However, to the best of our knowledge, the transform to make the process go to a specific state is not available. To extend the analysis in this article to Lévy processes, this task may be necessary.

Appendix

We demonstrate the calculation procedure for $q$ in (3.26) and (3.27) by using the end of December 2013 as a reference point. The values of $A$, $D$, $E$ and “interest paid” are displayed in millions of U.S. dollars.

(1) The value of equity $E$$(=135.43)$ is calculated as the difference between the market value of assets $A$$(=292.98)$ (estimated by the method in Sect. 4.1.1) and the value of debt $D$$(=157.55)$ (used in the estimation of $A$). Using these estimates, the weights of the equity and debt are determined as $w_{E}=\frac{E}{A}$ and $w_{D}=\frac{D}{A}$, respectively.

(2) We set the daily risk-free rates equal to daily 1-year US treasury yield curve rates divided by 360. The company’s $\beta$ is estimated by regressing (without intercept) the daily excess returns (of 2013) of the company stock on those of the NASDAQ composite price index. With this $\beta$$(=1.42)$, the annual NASDAQ return $R_{m}$$(=38.32\%)$ for 2013 and 1-year US treasury yield curve rate $R_{f}$$(=0.13\%)$ for the end of 2013, we calculate the cost of equity as $C_{E}=R_{f}+\beta (R_{m}-R_{f})=54.31\%$.

(3) Dividing “interest paid” ($=18.95$) from the cash flow statement of the year 2013 by the average of the debt values of December 2012 ($D_{2012}=117.05$) and December 2013 ($D_{2013}=157.55$) gives us the cost of debt $C_{D}=13.8\%$. The calculation of debt values is described in Sect. 4.1.1.

(4) Setting the corporate tax rate as $35\%$, we obtain

$$ q=w_{E} C_{E}+w_{D} C_{D} (1-0.35)=29.9306\%. $$