Behavior and mixing of a cold intermediate layer near a sloping boundary

Abstract

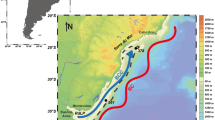
As in many other subarctic basins, a cold intermediate layer (CIL) is found during ice-free months in the Lower St. Lawrence Estuary (LSLE), Canada. This study examines the behavior of the CIL above the sloping bottom using a high-resolution mooring deployed on the northern side of the estuary. Observations show successive swashes/backwashes of the CIL on the slope at a semi-diurnal frequency. It is shown that these upslope and downslope motions are likely caused by internal tides generated at the nearby channel head sill. Quantification of mixing from 322 turbulence casts reveals that in the bottom 10 m of the water column, the time-average dissipation rate of turbulent kinetic energy is 𝜖 _{10 m} = 1.6×10⁻⁷Wkg⁻¹, an order of magnitude greater than found in the interior of the basin, far from boundaries. Near-bottom dissipation during the flood phase of the M₂ tide cycle (upslope flow) is about four times greater than during the ebb phase (downslope flow). Bottom shear stress, shear instabilities, and internal wave scattering are considered as potential boundary mixing mechanisms near the seabed. In the interior of the water column, far from the bottom, increasing dissipation rates are observed with both increasing stratification and shear, which suggests some control of the dissipation by the internal wave field. However, poor fits with a parametrization for large-scale wave-wave interactions suggests that the mixing is partly driven by more complex non-linear and/or smaller scale waves.

Appendix: Analytical solutions for the vertical modal structure of isopycnal displacements

In this Appendix, we re-derive the analytical expression for the vertical modal structure of the Poincaré wave for the isopycnal displacements η ₀(z) given a analytical density profile (Eq. 6).

1.1 A1 Problem formulation

For a certain vertical mode n, η ₀ is the solution of the ordinary differential equation (ODE) given by (e.g., Cushman-Roisin and Beckers, 2011):

$$ \frac{d^{2}\eta_{0}}{dz^{2}} + \left(\frac{N^{2}-\sigma^{2}}{{c_{n}^{2}}}\right)\eta_{0}=0, $$

(A1)

where $N^{2}=\frac {g}{\rho }\frac {\partial \rho }{\partial z} = \frac {gd}{(z+h)^{2}}$ given the density profile imposed by Eq. 6, and c _n the phase velocity that, as we will show later, depends on the vertical mode n. If we let $\nu ^{2} = \frac {gd}{{c_{n}^{2}}}$, and neglecting σ ² because N ²>>σ ², Eq. A1 can be re-written:

$$ \frac{d^{2}\eta_{0}}{dz^{2}} + \frac{\nu^{2}}{(z+h)^{2}}\eta_{0}=0. $$

(A2)

1.2 A2 Simplifications and general solution of the problem

To resolve the problem, we start by introducing two successive variable changes in order to scale the equation. We first introduce the non-dimensional parameter ξ such as z=ξ h ($d\xi = \frac {1}{h}dz$). Then, if we let ζ=ξ+1 (d ζ=d ξ), the ODE becomes:

$$ \frac{d^{2}\eta(z)}{d\zeta^{2}} + \frac{\nu^{2}}{\zeta^{2}}\eta=0. $$

(A3)

We now assume that the solution has the form η ₀(ζ)=A(ζ)B(ζ). After applying the derivative rules, the ODE is now:

$$\begin{array}{@{}rcl@{}} &A\frac{d^{2}B}{d\zeta^{2}} + 2A_{\zeta}\frac{dB}{d\zeta} + A_{\zeta\zeta}B + \frac{\nu^{2}}{\zeta^{2}}AB = 0\\ &\frac{d^{2}B}{d\zeta^{2}} + \frac{2A_{\zeta}}{A}\frac{dB}{d\zeta} + B\left[\frac{A_{\zeta\zeta}}{A} + \frac{\nu^{2}}{\zeta^{2}}\right] = 0. \end{array} $$

(A4)

where subscripts to variable A stand for derivative relative to ζ. The passage from the first to the second line of Eq. A4 was made by multiplying by 1/A.

We now choose A=ζ ^1/2. Knowing that:

$$\begin{array}{@{}rcl@{}} A_{\zeta} &= &\frac{1}{2\zeta^{1/2}}, \\ A_{\zeta\zeta} &=& \frac{-1}{4\zeta^{3/2}}, \\ \frac{A_{\zeta}}{A} &=& \frac{1}{2\zeta} ~~\text{and} \\ \frac{A_{\zeta\zeta}}{A} &=& \frac{-1}{4\zeta^{2}}, \end{array} $$

(A5)

and by multiplying Eq. A4 by ζ ², the ODE becomes:

$$ \zeta^{2}\frac{d^{2}B}{d\zeta^{2}} + \zeta\frac{dB}{d\zeta} + B\left[\nu^{2}-\frac{1}{4}\right] = 0. $$

(A6)

We now introduce a new variable change s= ln(ζ) (thus ζ=e ^S) which results in the following derivation rules:

$$\begin{array}{@{}rcl@{}} \frac{ds}{d\zeta} &=& \frac{1}{\zeta} = e^{-s}, \\ \frac{d}{d\zeta} &=& e^{-s}\frac{d}{ds}~~ \text{and} \\ \frac{d^{2}}{d\zeta^{2}} &=& e^{-2s}\left[\frac{d^{2}}{ds^{2}} - \frac{d}{ds}\right]. \end{array} $$

(A7)

With this variable change, the equation is:

$$ \frac{d^{2}B}{ds^{2}} + \left[\nu^{2}-\frac{1}{4}\right]B = 0. $$

(A8)

This last expression is a second-order homogeneous differential equation with constant coefficients that can be resolved with standard procedures (see any ODE textbook). The characteristic equation for this equation is λ ² + μ²=0, where ${\upmu }^{2} = \nu ^{2}-\frac {1}{4}$. Since μ² is positive by construction (this can be easily verified later), the characteristic equation leads to complex roots λ=±iμ. In this case, the analytical solution for the variable B has the form:

$$ B = C_{1}\cos(\upmu s) + C_{2} \sin(\upmu s), $$

(A9)

where C ₁ and C ₂ are constant coefficients to be determined.

1.3 A3 Specific solutions given the boundary conditions

Recalling that η ₀(ζ)=A(ζ)B(ζ) and A(ζ)=ζ ^1/2, we can now use the boundary conditions on η ₀ to find the specific solution of our problem. Because displacements are vertically limited by the seafloor and the surface, the boundary conditions are η ₀(z=0)=0 and η ₀(z=H) = 0, where H is the total depth. Given the variables changes made in the preceding, these boundary conditions imply B(s=0)=0 (i.e., z=0→ζ=1→s=0) and $Bs=\ln\left({H}/{h}+1\right)=0$ (i.e., $z = H \rightarrow \zeta =\frac {H}{h}+1 \rightarrow s=\ln \left (\frac {H}{h}+1\right )$).

The first boundary condition (at the surface) implies that C ₁ = 0, while the second condition implies that the argument under the sine must be of the form μs=n π, with n=1,2,..., an integer corresponding to the n^th vertical mode. Substituting $s=\ln {\left (\frac {H}{h}+1\right )}$ in the preceding, a necessary condition is that:

$$ \mu = \frac{n\pi}{\ln{\left(\frac{H}{h}+1\right)}}. $$

(A10)

After replacing all terms by their expressions in z and taking into consideration these boundary conditions, Eq. A9 becomes:

$$ \eta_{0}(z) = \eta_{n}\left(\frac{z}{h}+1\right)^{1/2}\sin \left[\frac{\ln{\left(\frac{z}{h}+1\right)}}{\ln{\left(\frac{H}{h}+1\right)}}n\pi \right]. $$

(A11)

Note that in the last expression, C ₂ has been replaced by η _n for clarity and is the parameter that carries the dimension (m) of η ₀. This constant parameter is determined by fitting Eq. A11 to observations. Note also that Eq. A11 is slightly different than the one presented in Forrester (1974) (its Eq. 10), but by carefully adjusting the constant parameters in Forrester’s equation, we can show that both equations give the same structure.

Another consequence of the second boundary condition (Eq. A10) is that it gives conditions on the phase velocity (c _n ) of the admissible Poincaré waves. Replacing μ by its expression in z this equation leads to:

$$ {c_{n}^{2}} = \frac{gd}{\left( \frac{n\pi}{\ln\left( \frac{H}{h}+1 \right)} \right)^{2} + \frac{1}{4}}. $$

(A12)

This expression is necessary for the dispersion relation presented in Eq. 5.