Viscous Taylor droplets in axisymmetric and planar tubes: from Bretherton’s theory to empirical models

Abstract

The aim of this study is to derive accurate models for quantities characterizing the dynamics of droplets of non-vanishing viscosity in capillaries. In particular, we propose models for the uniform-film thickness separating the droplet from the tube walls, for the droplet front and rear curvatures and pressure jumps, and for the droplet velocity in a range of capillary numbers, Ca, from $10^{-4}$ to 1 and inner-to-outer viscosity ratios, $\lambda$, from 0, i.e. a bubble, to high-viscosity droplets. Theoretical asymptotic results obtained in the limit of small capillary number are combined with accurate numerical simulations at larger Ca. With these models at hand, we can compute the pressure drop induced by the droplet. The film thickness at low capillary numbers ($Ca<10^{-3}$) agrees well with Bretherton’s scaling for bubbles as long as $\lambda <1$. For larger viscosity ratios, the film thickness increases monotonically, before saturating for $\lambda>10^3$ to a value $2^{2/3}$ times larger than the film thickness of a bubble. At larger capillary numbers, the film thickness follows the rational function proposed by Aussillous and Quéré (Phys Fluids 12(10):2367–2371, 2000) for bubbles, with a fitting coefficient which is viscosity-ratio dependent. This coefficient modifies the value to which the film thickness saturates at large capillary numbers. The velocity of the droplet is found to be strongly dependent on the capillary number and viscosity ratio. We also show that the normal viscous stresses at the front and rear caps of the droplets cannot be neglected when calculating the pressure drop for $Ca>10^{-3}$.

Appendices

Appendix 1: Derivation of the flow profiles in the thin-film region for the planar configuration

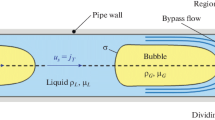
Consider an axial location in the thin-film region. The velocity profiles inside, $u_i$, and outside, $u_o$, of the droplet can be described by:

$$\begin{aligned} u_i(r)&= {} \frac{1}{2 \mu _i} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} r^2 + A_i r + B_i,\end{aligned}$$

(52)

$$\begin{aligned} u_o(r)&= {} \frac{1}{2 \mu _o} \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} r^2 + A_o r + B_o, \end{aligned}$$

(53)

where $p_i$ and $p_o$ are the inner, respectively outer, pressures, and $A_i$, $B_i$, $A_o$ and $B_o$ are real constants to be determined. Given the symmetry at $r=0$ of the inner velocity, $A_i=0$. The other constants are found by imposing the no-slip boundary condition at the channel walls $u(R) = -U_d$ in the droplet reference frame, the continuity of velocities at the interface located at $r=R-H$, $u_i(R-H) = u_o(R-H)$, and the continuity of tangential stresses at the interface

$$\begin{aligned} \mu _i \frac{\mathrm{{d}} u_i}{\mathrm{{d}}z}\bigg \vert _{r=R-H} = \mu _o \frac{\mathrm{{d}} u_o}{\mathrm{{d}}z}\bigg \vert _{r=R-H}. \end{aligned}$$

(54)

Eventually one obtains:

$$\begin{aligned} A_o&= {} \frac{1}{\mu _o} \left( \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}-\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) (R-H),\end{aligned}$$

(55)

$$\begin{aligned} B_i= {} \frac{1}{2 \mu _i \mu _o} \left[ -(R - H)^2\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \mu _o + H \left( 2 H \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} - H \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} - 2 R \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \right) \mu _i \right] -U_d,\end{aligned}$$

(56)

$$\begin{aligned} B_o&= {} \frac{1}{2 \mu _o}\left[ \left( \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} - 2\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \right) R^2- 2 H R \left( \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} - \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \right) \right] -U_d. \end{aligned}$$

(57)

Appendix 2: Derivation of the interface profile equation for the planar configuration

The flow rates at any axial location where the external film thickness is H are:

$$\begin{aligned} q_i&= {} 2 \int _0^{R-H} u_i(r) \mathrm{{d}}r \nonumber \\&= {} \frac{1}{3\mu _i\mu _o}\left\{ -(R-H)\left[ 3 H \left( H \left( \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} -2 \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} \right) +2\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} R\right) \mu _i \right. \right. \nonumber \\&+ \left. \left. 2 \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} (R-H)^2\mu _o\right] \right\} -2U_d (R-H), \end{aligned}$$

(58)

$$\begin{aligned} q_o&= {} 2 \int _{R-H}^{R} u_o(r) \mathrm{{d}}r \nonumber \\&= {} \frac{H^2}{3\mu _o}\left[ H\left( 3\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} -2\frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\right) -3\frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} R\right] -2 U_d H. \end{aligned}$$

(59)

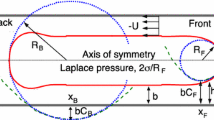
In the droplet reference frame, the flow rate of the inner phase has to vanish, $q_i =0$. Furthermore, in the region where the film is uniform (see Fig. 11), $H=H_{\infty }$, the inner and outer pressure gradients have to be equal. Using these two conditions, one can solve for the pressure gradient in the uniform film region

$$\begin{aligned} \frac{\mathrm{{d}} p}{\mathrm{{d}}z} \bigg \vert _{r=R-H_{\infty }} \approx -\frac{6 \mu _i U_d}{2 R^2-(4 -6\lambda ) H_{\infty } R + (2-3 \lambda ) H_{\infty }^2} \end{aligned}$$

(60)

and for the outer flow rate, where the limit $H_{\infty }/R \ll 1$ is considered:

$$\begin{aligned} q_o\approx & {} -2 H_{\infty } \left[ \frac{2 R^2 - (4-3 \lambda ) H_{\infty } R +2(1- \lambda ) H_{\infty }^2 }{ 2R^2 - (4 -6\lambda ) H_{\infty } R+(2-3 \lambda ) H_{\infty }^2}\right] U_d \nonumber \\\approx & {} -H_{\infty } \left[ \frac{2 R - (4-3 \lambda ) H_{\infty } }{ R - (2 -3\lambda ) H_{\infty } }\right] U_d. \end{aligned}$$

(61)

The pressure gradients in the dynamic meniscus regions are no longer equal and their difference is proportional to the deformation of the interface $r=R-H$. Under the assumption of a quasi-parallel flow, and neglecting the viscous contribution in view of the lubrication assumption, the Laplace’s law imposes:

$$\begin{aligned} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z} - \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z} = \gamma \frac{\mathrm{{d}}^3 H}{\mathrm{{d}} z^3}. \end{aligned}$$

(62)

Knowing $q_i$ and $q_o$, Eqs. (58), (59) can be solved for the unknown pressure gradients $\mathrm{{d}}p_i/\mathrm{{d}}z$, $\mathrm{{d}}p_o/\mathrm{{d}}z$ as a function of H:

$$\begin{aligned} \frac{\mathrm{{d}} p_i}{\mathrm{{d}}z}\approx & {} \frac{ 3\lambda \left\{ 2H\left[ H_{\infty }(3\lambda -2)+R\right] -3H_{\infty }\left[ H_{\infty }(3\lambda -4)+2R\right] \right\} \mu _oU_d}{H(R-H)\left[ H(3\lambda -4)+4R\right] \left[ H_{\infty }(3\lambda -2)+R\right] },\end{aligned}$$

(63)

$$\begin{aligned} \frac{\mathrm{{d}} p_o}{\mathrm{{d}}z}\approx & {} -6 \left\{ \frac{R(H-H_{\infty })\left[ 3\lambda (H+H_{\infty })-2(H+2H_{\infty })\right] }{H^3\left[ H(3\lambda -4)+4R\right] \left[ H_{\infty }(3\lambda -2)+R\right] }\right. \nonumber \\&\left. +\frac{H H_{\infty }[H(2-3\lambda )^2+H_{\infty }(3(5-3\lambda )\lambda -4)]+2R^2(H-H_{\infty })}{H^3\left[ H(3\lambda -4)+4R\right] \left[ H_{\infty }(3\lambda -2)+R\right] }\right\} \mu _o U_d \end{aligned}$$

(64)

and substituted into Eq. (62). Following Bretherton (1961), the resulting equation can be put in an universal form by the substitutions $H = H_{\infty } \eta$ and $z = H_{\infty } (3 Ca)^{-1/3} \xi$. In the limit of $H_{\infty }/R\rightarrow 0$, the governing equation for the interface profile reads:

$$\begin{aligned} \frac{{\text {d}}^3 \eta }{{\text {d}}\xi ^3} =2\frac{\eta -1}{\eta ^3}\left[ \frac{2+3 m (1+ \eta + 3 m \eta )}{(1+3m)(4+3m\eta )}\right]. \end{aligned}$$

(65)

where

$$\begin{aligned} m = \lambda \frac{H_{\infty }}{R} \end{aligned}$$

(66)

is the rescaled viscosity ratio.

Appendix 3: Derivation of the droplet velocity model for the planar configuration

The velocity profiles in the uniform film region have been derived in “Appendix 1”. In particular, the inner and outer volumetric fluxes are given by Eqs. (58) and (59), respectively. At the location where $H=H_{\infty }$ the interface is flat and the pressure gradients are equal, $\mathrm{{d}}p_i/\mathrm{{d}}z=\mathrm{{d}}p_o/\mathrm{{d}}z=\mathrm{{d}}p/\mathrm{{d}}z$. Furthermore, mass conservation imposes that $q_o= 2R (U_{\infty }-U_d)$ and since we are in the reference frame of the droplet, $q_i=0$. The system of two equations can be solved for the pressure gradient

$$\begin{aligned} \frac{\mathrm{{d}} p}{\mathrm{{d}}z} \bigg \vert _{r=R-H_{\infty }} = \frac{-3 R U_{\infty } \mu _i}{(R-H_{\infty })^3+H_{\infty }(3R^2-3H_{\infty }R +H_{\infty }^2)\lambda } \end{aligned}$$

(67)

and the droplet velocity

$$\begin{aligned} U_d= \frac{R[2(R-H_{\infty })^2+3 H_{\infty }(2R-H_{\infty })\lambda ]}{2(R-H_{\infty })^3+2H_{\infty }(3R^2-3H_{\infty }R+H_{\infty }^2)\lambda }U_{\infty }. \end{aligned}$$

(68)

The relative velocity of the planar droplet reads

$$\begin{aligned} \frac{U_d-U_{\infty }}{U_d} = \frac{\frac{H_{\infty }}{R} \left\{ 2-\frac{H_{\infty }}{R} \left[ 4+2 \frac{H_{\infty }}{R}(\lambda -1) -3 \lambda \right] \right\} }{2+\left( 2-\frac{H_{\infty }}{R}\right) \frac{H_{\infty }}{R}(3\lambda -2)}. \end{aligned}$$

(69)

Appendix 4: Derivation of the critical uniform film thickness for the appearance of the recirculation regions

The velocity profile in the channel away from the droplet is given by Eq. (11) for the axisymmetric configuration and by

$$\begin{aligned} u_{\infty }(y) = \frac{3}{2} U_{\infty }\left[ 1-\left( \frac{y}{R}\right) ^2\right] -U_d \end{aligned}$$

(70)

for the planar one. The droplet velocity for the former case is given by Eq. (32), whereas for the latter it is given by Eq. (68). With the use of Eqs. (32) and (68), the velocity $u_{\infty }$ can be expressed as a function of $H_{\infty }/R$. The critical uniform film thickness for the appearance of recirculation regions, $H_{\infty }^{\star }$, is obtained by solving $u_{\infty }(0) = 0$, resulting in Eqs. (12) and (13) for the axisymmetric and planar configurations, respectively.

Appendix 5: Fitting laws for the model coefficients

The model coefficients Q in Eq. (30), G in Eq. (38), $T_{f,r}$ and $Z_{f,r}$ in Eq. (41) and $M_{f,r}$, $N_{f,r}$ and $O_{f,r}$ in Eq. (44) can be well approximated by the rational function

$$\begin{aligned} \frac{a_3 \lambda ^3+a_2 \lambda ^2+a_1 \lambda + a_0 }{\lambda ^3+b_2 \lambda ^2 +b_1 \lambda + b_0}, \end{aligned}$$

(71)

where the constants $a_i$ with $i=0,..,3$ and $b_j$ with $j=0,..,2$ are given in Tables 1 and 2 for the axisymmetric and planar geometries, respectively.

Table 1 Coefficients of the fitting law for the axisymmetric configuration

Table 2 Coefficients of the fitting law for the planar configuration

Appendix 6: Additional results

For the sake of clarity, the results for $\lambda = 0$ and 100 are shown in the appendix rather than in the main text, except for the normal viscous stresses jump, whose results for $\lambda = 0$ are presented in the main text as for $\lambda = 1$ the normal viscous stress jumps are small (Figs. 25, 26, 27, 28, 29, 30).

Fig. 25

Uniform film thickness given by Eq. (30) (lines) and FEM-ALE numerical results (symbols) as a function of the droplet capillary number for $\lambda = 0$ (a) and 100 (b) and both axisymmetric (blue solid line, full symbols) and planar (dashed red line, empty symbols) geometries. (Color figure online)

Fig. 26

Minimum film thickness given by Eq. (38) (lines) and FEM-ALE numerical results (symbols) as a function of the droplet capillary number for $\lambda = 0$ (a) and 100 (b) and both axisymmetric (blue solid line, full symbols) and planar (dashed red line, empty symbols) geometries. (Color figure online)

Fig. 27

Curvature $\kappa _f$ of the front meniscus predicted by the model Eq. (41) (lines) and FEM-ALE data (symbols) versus Ca for both axisymmetric (blue line, full symbols) and planar (red dashed line, empty symbols) geometries, where the viscosity ratio is $\lambda = 0$ (a) and 100 (b). (Color figure online)

Fig. 28

The rear counterpart $\kappa _r$ of Fig. 27. (Color figure online)

Fig. 29

Front pressure jump $\Delta p_f$ given by Eq. (43) (solid lines) and front normal viscous stress jump $\Delta \tau _{{zz}_{f}}$ by Eq. (44) (inset, solid lines) and FEM-ALE data (symbols) versus Ca for both axisymmetric (blue line, full symbols) and planar (red line, empty symbols) geometries, where the viscosity ratio is $\lambda = 1$ (a) and 100 (b). The dashed lines correspond to the improved pressure jump model Eq. (46). Note the different scale in the insets. (Color figure online)

Fig. 30

The rear counterpart, pressure jump $\Delta p_r$ and normal viscous stress jump $\Delta \tau _{{zz}_{r}}$, of Fig. 29. (Color figure online)

Fig. 31

Pressure correction due to non-parallel flow effects at the rear (a) and front (b) outer sides of the interface for $\lambda = 0.04$ (blue squares), 0.12 (red crosses), 1 (yellow circles), 15 (purple stars) and 50 (green diamonds) for the axisymmetric configuration. The results are obtained from FEM-ALE numerical simulations. (Color figure online)

Fig. 32

Pressure correction due to non-parallel flow effects at the rear (a) and front (b) inner sides of the interface for $\lambda = 0.04$ (blue squares), 0.12 (red crosses), 1 (yellow circles), 15 (purple stars) and 50 (green diamonds) for the axisymmetric configuration. The results are obtained from FEM-ALE numerical simulations. (Color figure online)

Appendix 7: Pressure corrections due to non-parallel flow

Some typical total stresses corrections at the outer and inner sides of the droplet interface as a function of Ca and for different viscosity ratios $\lambda$ are shown in Figs. 31 and 32, respectively.