On the planar central configurations of rhomboidal and triangular four- and five-body problems

Abstract

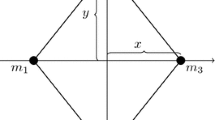
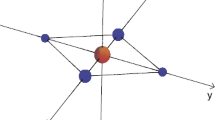
We consider a symmetric five-body problem with three unequal collinear masses on the axis of symmetry. The remaining two masses are symmetrically placed on both sides of the axis of symmetry. Regions of possible central configurations are derived for the four- and five-body problems. These regions are determined analytically and explored numerically. The equations of motion are regularized using Levi-Civita type transformations and then the phase space is investigated for chaotic and periodic orbits by means of Poincaré surface of sections.

Appendix

1.1 Derivation of $R_{N_{\mu_{0}}}$

The numerator of $\mu_{0}$, $N_{\mu_{0}}$ is positive when ${A}_{ {1}}{C}_{{2}}{C}_{{3}}>0$ and ${B}_{{1}}{B}_{{3}}{C}_{{2}}+{B}_{ {2}}{C}_{{1}}{C}_{{3}}<0$ or when both factors have opposite sign and the positive factor is greater than the absolute value of the negative factor. All these possibilities are listed below with the corresponding regions, where $N_{\mu_{0}}>0$:

• 1. ${A}_{{1}}{C}_{{2}}{C}_{{3}}>0$ and ${B}_{{1}}{B}_{{3}}{C}_{{2}}+ {B}_{{2}}{C}_{{1}}{C}_{{3}}<0$: Using numerical approximation techniques we see that $N_{\mu_{0}}>0$ in the following region:

  $$ R_{cN_{\mu_{0}}}(t,w)=R_{aN_{\mu_{0}}}(t,w)\cup R_{bN_{\mu_{0}}}(t,w), $$

  (56)

  where

  $$\begin{aligned} R_{aN_{\mu_{0}}}(t,w) =&\bigl\{ (t,w)|(0< t< 0.41\wedge0< w< 1) \\ &{}\vee(0.41< t< 1\wedge w>2.41)\vee\bigl(-1.73 \\ &{}< w\leq-1.5\wedge0.75\cdot d_{2}(w)< t< 1\bigr)\bigr\} , \\ R_{bN_{\mu_{0}}}(t,w) =&(w< -1.8\wedge0< t< 0.23)\vee(-1.43 \\ &{}< w\leq-1\wedge0.56< t< 1)\vee(-1< w \\ &{}< -0.41\wedge0.41< t< -w)\vee(2< w \\ &{}< 2.41\wedge0.41< t< 1). \end{aligned}$$

• 2. ${A}_{{1}}{C}_{{2}}{C}_{{3}}>0$ and ${B}_{{1}}{B}_{{3}}{C}_{{2}}+ {B}_{{2}}{C}_{{1}}{C}_{{3}}>0$. It is numerically confirmed that ${B}_{{1}}{B}_{{3}}{C}_{{2}}+{B}_{{2}}{C}_{{1}}{C}_{{3}}>{A}_{{1}} {C}_{{2}}{C}_{{3}}$ when ${A}_{{1}}{C}_{{2}}{C}_{{3}}>0$. Hence, $N_{\mu_{0}}<0$ for all $(t,w)$ such that ${A}_{{1}}{C}_{{2}}{C}_{ {3}}>0$.

• 3. ${A}_{{1}}{C}_{{2}}{C}_{{3}}<0$ and ${B}_{{1}}{B}_{{3}}{C}_{{2}}+ {B}_{{2}}{C}_{{1}}{C}_{{3}}<0$. In this case using numerical approximation techniques we find that $N_{\mu_{0}}$ is positive in the following region:

  $$\begin{aligned} R_{dN_{\mu_{0}}}(t,w) =&\bigl\{ (t,w)|(-1.73< w< -1.5 \\ &{}\wedge 0< t< 0.25)\vee\bigl(-1.5\leq w< -1 \\ &{}\wedge 0< t< 0.2\cdot d_{2}(w)\bigr)\vee(0< t< 0.41 \\ &{}\wedge -t< w < 0) \vee(0.41< t< 1 \\ &{}\wedge 0< w< 1)\bigr\} . \end{aligned}$$

Hence, $N_{\mu_{0}}>0$ in (see Fig. 9b)

$$ R_{N_{\mu_{0}}}=R_{cN_{\mu_{0}}}(t,w)\cup R_{dN_{\mu_{0}}}(t,w). $$

(57)

1.2 Derivation of $R_{N_{\mu_{2}}}$

The numerator of $\mu_{2}$, $N_{\mu_{2}}$, is always positive when $A_{3}B_{2}C_{1} >0$ and $A_{1}A_{3}C_{2}+A_{2}C_{1}C_{3}<0$. It is not necessarily positive when $A_{3}B_{2}C_{1}>0$ and $A_{1}A_{3}C_{2}+A _{2}C_{1}C_{3}<0$ or $A_{3}B_{2}C_{1}<0$ and $A_{1}A_{3}C_{2}+A_{2}C _{1}C_{3}<0$. It might be positive in a segment of this region or might not be positive at all. We will list all these possibilities below with the corresponding regions, where $N_{\mu_{2}}>0$.

• 1. $A_{3}B_{2}C_{1}>0$ and $A_{1}A_{3}C_{2}+A_{2}C_{1}B_{3}<0$. Using numerical approximation techniques we show that $N_{\mu_{2}}>0$ in

  $$\begin{aligned} R_{aN_{\mu_{2}}}(t,w) =&aaN_{\mu_{2}}(t,w)\cup baN_{\mu_{2}}(t,w) \\ &{}\cup caN _{\mu_{2}}(t,w), \end{aligned}$$

  (58)

  where

  $$\begin{aligned} aaN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|\bigl(0< w\leq0.41\wedge d_{1}(w) \\ &{}< t< 1\bigr) \vee\bigl(0.41< w< 0.58 \\ &{}\wedge d_{1}(w)< t< 0.5\cdot d_{2}(w)\bigr) \\ &{}\vee\bigl(w>\sqrt{3}\wedge0< t< d_{1}(w)\bigr)\bigr\} , \\ baN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|(w\leq-2.41\wedge0.463 \\ &{}- 0.079\cdot w < t< 1)\vee\bigl(-2.41< w \\ &{}< -1.73\wedge0.463-0.079w \\ &{}< t < 0.5 d_{2}(w)\bigr)\bigr\} , \\ caN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|1< w< 1.73 \wedge 0< t< d_{1}(w)\bigr\} . \end{aligned}$$

• 2. $A_{3}B_{2}C_{1}>0$ and $A_{1}A_{3}C_{2}+A_{2}C_{1}B_{3}>0$. Using numerical approximation techniques we show that $N_{\mu_{2}}>0$ in

  $$\begin{aligned} R_{bN_{\mu_{2}}}(t,w) =& abN_{\mu_{2}}(t,w)\cup bbN_{\mu_{2}}(t,w) \\ &{}\cup cbN _{\mu_{2}}(t,w), \end{aligned}$$

  (59)

  where

  $$\begin{aligned} abN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|{-}1.73< w< -1 \\ &{}\wedge 0< t< 0.5\cdot d_{2}(w)\bigr\} , \\ bbN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|1< w< 1.73 \wedge 0< t< d_{1}(w)\bigr\} , \\ cbN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|(w\leq-2.41\wedge 0< t< 1) \\ &{}\vee\bigl(-2.41< w< -1.73 \\ &{}\wedge 0< t< 0.5\cdot d_{2}(w)\bigr)\bigr\} . \end{aligned}$$

• 3. $A_{3}B_{2}C_{1}<0$ and $A_{1}A_{3}C_{2}+A_{2}C_{1}B_{3}<0$. Using numerical approximation techniques we show that $N_{\mu_{2}}>0$ in

  $$ R_{cN_{\mu_{2}}}(t,w)=acN_{\mu_{2}}(t,w)\cup bcN_{\mu_{2}}(t,w), $$

  (60)

  where

  $$\begin{aligned} acN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|\bigl(-2.4< w< -2 \\ &{}\wedge 0.5\cdot d_{2}(w)< t< 1\bigr)\vee \\ &{}\wedge \bigl(1< w< 1.73\wedge d_{1}(w)< t< 1\bigr)\bigr\} , \\ bcN_{\mu_{2}}(t,w) =&\bigl\{ (t,w)|\bigl(1.31\cdot t^{2}-2.012 \cdot t+0.9 \\ &{}< w< 0.58\wedge0< t< d_{1}(w)\bigr) \\ &{}\vee \bigl(1.31\cdot t^{2}-2.012 \cdot t+0.9\leq w< 1 \\ &{}\wedge 0< t< 0.5 \cdot d_{2}(w)\bigr) \\ &{}\vee \bigl(w>1.732\wedge d_{1}(w)< t< 1\bigr)\bigr\} . \end{aligned}$$

  Therefore, $N_{\mu_{2}}(t,w)>0$ in the region

  $$ R_{N_{\mu_{2}}}=R_{aN_{\mu_{2}}}(t,w)\cup R_{bN_{\mu_{2}}}(t,w)\cup R _{cN_{\mu_{2}}}(t,w). $$

  (61)

1.3 Derivation of $R_{N_{\mu_{4}}}$

$N_{\mu_{4}}$ is always positive when $A_{2}B_{1}C_{3}>0$ and $A_{3}B_{1}B_{2}+A_{1}A_{2}C_{3}<0$. It is not necessarily positive when $A_{2}B_{1}C_{3}>0$ and $A_{3}B_{1}B_{2}+A_{1}A_{2}C_{3}<0$ or when both factors are negative. It might be positive in a segment of this region or might not be positive at all. We will list all these possibilities below with the corresponding regions, where $N_{\mu_{4}}>0$.

• 1. When $A_{2}B_{1}C_{3}>0$, and $A_{3}B_{1}B_{2}+A_{1}A_{2}C_{3}<0$, $N_{\mu_{4}}> 0$ in the region

  $$\begin{aligned} R_{aN_{\mu_{4}}} =&\bigl\{ (t,w)|(1.73< w< 2.4\wedge0.< t< d_{1}) \\ &{}\vee (-1< w< -0.41\wedge-w< t< 1) \\ &{}\vee (0< w< 1 \wedge d_{1}< t< 1) \\ &{}\vee \bigl(w< -377.64t^{4}+677.58t^{3}-458.06t^{2} \\ &{}+136.9t-17.79\wedge0.25< t< 0.6\bigr) \\ &{}\vee (-1< w< -0.41\wedge0< t< 0.05) \\ &{}\vee (1.73< w< 2.41\wedge d_{1}< t< 0.41)\bigr\} . \end{aligned}$$

• 2. When $A_{2}B_{1}C_{3}>0$, and $A_{3}B_{1}B_{2}+A_{1}A_{2}C_{3}>0$, $N_{\mu_{4}}> 0$ in the region

  $$\begin{aligned} R_{bN_{\mu_{4}}} =&\bigl\{ (t,w)|(0.1< w< 1\wedge0.41< t< d_{1}) \\ &{}\vee (1< w< 1.73\wedge d_{1}< t< 0.41) \\ &{}\vee (1.73< w< 2.41\wedge0.41< t< 1) \\ &{}\vee (-1< w< -0.41\wedge-w< t< 1) \\ &{}\vee (0< w< 1\wedge d_{1}< t< 1) \\ &{}\vee (1< w< 1.73\wedge0< t< d_{1}) \\ &{}\vee \bigl(1.31t^{2}-2t+0.9< w< 1 \wedge 0< t< 0.41\bigr) \\ &{}\vee (1< w< 1.73\wedge0.41< t< 1) \\ &{}\vee (1.73< w< 2.41\wedge d_{1}< t< 0.41)\bigr\} . \end{aligned}$$

• 3. When $A_{2}B_{1}C_{3}<0$, and $A_{3}B_{1}B_{2}+A_{1}A_{2}C_{3}<0$, $N_{\mu_{4}}>0$ in the region

  $$\begin{aligned} R_{cN_{\mu_{4}}} =&\bigl\{ (t,w)|(-0.41< w< 0\wedge0< t< -w) \\ &{}\vee\bigl(w< -1.3t^{2}-1.9t+3.44 \\ &{}\wedge d_{1}< t< 0.41\bigr) \\ &{}\vee(w>2.41\wedge0< t< d_{1})\bigr\} . \end{aligned}$$

  Therefore, $N_{\mu_{4}}(t,w)>0$ in (see Fig. 11a)

  $$ R_{N_{\mu_{4}}}=R_{aN_{\mu_{4}}}(t,w)\cup R_{bN_{\mu_{4}}}(t,w)\cup R _{cN_{\mu_{4}}}(t,w). $$

  (62)