Secular and tidal evolution of circumbinary systems

Abstract

We investigate the secular dynamics of three-body circumbinary systems under the effect of tides. We use the octupolar non-restricted approximation for the orbital interactions, general relativity corrections, the quadrupolar approximation for the spins, and the viscous linear model for tides. We derive the averaged equations of motion in a simplified vectorial formalism, which is suitable to model the long-term evolution of a wide variety of circumbinary systems in very eccentric and inclined orbits. In particular, this vectorial approach can be used to derive constraints for tidal migration, capture in Cassini states, and stellar spin–orbit misalignment. We show that circumbinary planets with initial arbitrary orbital inclination can become coplanar through a secular resonance between the precession of the orbit and the precession of the spin of one of the stars. We also show that circumbinary systems for which the pericenter of the inner orbit is initially in libration present chaotic motion for the spins and for the eccentricity of the outer orbit. Because our model is valid for the non-restricted problem, it can also be applied to any three-body hierarchical system such as star–planet–satellite systems and triple stellar systems.

Appendices

Appendix 1: Oblate spheroid potential

The gravitational potential of an oblate body of mass $m_i$ symmetric about its rotation axis $\hat{\mathbf {s}}$ is given by (e.g. Goldstein 1950):

$$\begin{aligned} V_{i} (\mathbf {r}) = - G \frac{m_i}{r} \left[ 1 - J_{2,i} \left( \frac{R_i}{r}\right) ^2 P_2 (\hat{\mathbf {r}} \cdot \hat{\mathbf {s}}_i) \right] , \end{aligned}$$

(93)

where we neglected terms in $(R_i/r)^3$. The gravity field coefficient $J_{2,i}$ is obtained from the principal moments of inertia $A_i= B_i$ and $C_i$ as $J_{2,i} = (C_i-A_i) / m_iR_i^2$. When the asymmetry in the body mass distribution results only from its rotation, $J_{2,i}$ is given by expression (2). The main term in the above expression is responsible for the orbital motion (Eq. 4), while the contribution in $J_{2,i}$ is responsible for a perturbation of this motion, since $J_{2,i} (R_i/r)^2 \ll 1$. Thus, retaining only the terms in $J_{2,i}$, the resulting perturbing potential energy of a system composed of three oblate bodies is given by:

$$\begin{aligned} U_R = U_{R,0} + U_{R,1} + U_{R,2}, \end{aligned}$$

(94)

where we have for the planet

$$\begin{aligned} U_{R,2} = \sum _{i= 0,1} m_iV_{2} (\mathbf {r}_{2i}) = \sum _{i= 0,1} G \frac{m_im_2}{r_{2i}} J_{2,2} \left( \frac{R_2}{r_{2i}}\right) ^2 P_2 (\hat{\mathbf {r}}_{2i} \cdot \hat{\mathbf {s}}_2), \end{aligned}$$

(95)

and for each star ($i= 0, 1$)

$$\begin{aligned} U_{R,i} = G \frac{m_0m_1}{r_1} J_{2,i} \left( \frac{R_i}{r_1}\right) ^2 P_2 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {s}}_i) + G \frac{m_im_2}{r_{2i}} J_{2,i} \left( \frac{R_i}{r_{2i}}\right) ^2 P_2 (\hat{\mathbf {r}}_{2i} \cdot \hat{\mathbf {s}}_i). \end{aligned}$$

(96)

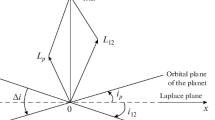
We also have (Fig. 1)

$$\begin{aligned} \mathbf {r}_{2i} = \mathbf {r}_2+ \delta _i\mathbf {r}_1, \end{aligned}$$

(97)

where $\delta _0= m_1/ m_{01}$ and $\delta _1= - m_0/ m_{01}$. Since we assume that $r_1\ll r_2$, we can write

$$\begin{aligned} \frac{P_2 (\hat{\mathbf {r}}_{2i} \cdot \hat{\mathbf {s}}_j)}{r_{2i}^3}\approx & {} \frac{P_2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {s}}_j)}{r_2^3} + \frac{3 \delta _i}{2 r_2^3} \frac{r_1}{r_2} \left[ \hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_2- 5 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_2) (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {s}}_j)^2\right. \nonumber \\&\left. + 2 (\hat{\mathbf {r}}_1\cdot \mathbf {s}_j) (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {s}}_j) \right] , \end{aligned}$$

(98)

where we neglected terms in $(r_1/ r_2)^2$, that is, we neglect terms in $J_{2,i} (R_i/r_i)^2 (r_1/ r_2)^2$ in the potential energy. Replacing in expressions (96) and (95) we get for the planet

$$\begin{aligned} U_{R,2} = G \frac{m_2m_{01}}{r_2} J_{2,2} \left( \frac{R_2}{r_2} \right) ^2 P_2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {s}}_2), \end{aligned}$$

(99)

since $m_0\delta _0+ m_1\delta _1= 0$, and for each star ($i= 0,1$; $j=1-i$)

$$\begin{aligned} U_{R,i}= & {} G \frac{m_0m_1}{r_1} J_{2,i} \left( \frac{R_i}{r_1}\right) ^2 \left[ P_2 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {s}}_i) + \frac{m_2}{m_j} \left( \frac{r_1}{r_2} \right) ^3 P_2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {s}}_i) \right] \nonumber \\\approx & {} G \frac{m_0m_1}{r_1} J_{2,i} \left( \frac{R_i}{r_1}\right) ^2 P_2 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {s}}_i), \end{aligned}$$

(100)

since terms in $m_2/ m_j(r_1/r_2)^3$ can also be neglected.

Appendix 2: Tidal potential

The tidal potential of a body of mass $m_i$ when deformed by another body of mass $m'$ at the position $\mathbf {r}'$ is given by (e.g. Kaula 1964):

$$\begin{aligned} V_{i} (\mathbf {r}, \mathbf {r}', m') = - k_{2,i} \frac{G m' R_i^5}{r^3 r'^3} P_2 (\hat{\mathbf {r}} \cdot \hat{\mathbf {r}}'), \end{aligned}$$

(101)

where we neglected terms in $(R_i/r)^4 (R_i/r')^4$. The resulting perturbing potential energy of a system composed of three bodies is given by:

$$\begin{aligned} U_T = U_{T,0} + U_{T,1} + U_{T,2}, \end{aligned}$$

(102)

where we have for the planet

$$\begin{aligned} U_{T,2} = \sum _{i,j=0,1} m_iV_{2} (\mathbf {r}_{2i}, \mathbf {r}_{2j}', m_j) = \sum _{i,j=0,1} - k_{2,2} \frac{G m_im_jR_2^5}{r_{2i}^3 r_{2j}'^3} P_2 (\hat{\mathbf {r}}_{2i} \cdot \hat{\mathbf {r}}_{2j}'), \end{aligned}$$

(103)

and for each star ($i= 0,1$; $j=1-i$)

$$\begin{aligned} U_{T,i} = m_j\left[ V_{i} (\mathbf {r}_1, \mathbf {r}_1', m_j) + V_{i} (\mathbf {r}_1, \mathbf {r}_{2i}', m_2) \right] + m_2\left[ V_{i} (\mathbf {r}_{2i}, \mathbf {r}_1', m_j) + V_{i} (\mathbf {r}_{2i}, \mathbf {r}_{2i}', m_2) \right] .\nonumber \\ \end{aligned}$$

(104)

Neglecting the tidal interactions with the external body $m_2$, i.e., neglecting terms in $m_2/ m_j(r_1/r_2)^3$, the above potential can be simplified as

$$\begin{aligned} U_{T,i} \approx m_iV_{i} (\mathbf {r}_1, \mathbf {r}_1', m_j) = - k_{2,i} \frac{G m_j^2 R_i^5}{r_1^3 r_1'^3} P_2 \left( \hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_1'\right) . \end{aligned}$$

(105)

Using expression (97) we can rewrite

$$\begin{aligned} \frac{P_2 (\hat{\mathbf {r}}_{2i} \cdot \hat{\mathbf {r}}_{2j}')}{r_{2i}^3 r_{2j}'^3}\approx & {} \frac{P_2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2')}{r_2^3 r_2'^3} + \frac{3 \delta _i}{2 r_2^3 r_2'^3} \frac{r_1}{r_2} \left[ \hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_2- 5 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_2) (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2')^2 + 2 (\hat{\mathbf {r}}_1\cdot \hat{\mathbf {r}}_2')(\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2') \right] \nonumber \\&+ \frac{3 \delta _j}{2 r_2^3 r_2'^3} \frac{r_1'}{r_2'} \left[ \hat{\mathbf {r}}_1' \cdot \hat{\mathbf {r}}_2' - 5 (\hat{\mathbf {r}}_1' \cdot \hat{\mathbf {r}}_2')(\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2')^2 + 2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_1')(\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2')\right] , \end{aligned}$$

(106)

where we neglected terms in $(r_1/ r_2)^2$, that is, we neglect terms in $(R_2/r_2)^6 (r_1/ r_2)^2$ in the potential energy. Replacing in expression (103) we get for the planet

$$\begin{aligned} U_{T,2} = - k_{2,2} \frac{G m_{01}^2 R_2^5}{r_2^3 r_2'^3} P_2 (\hat{\mathbf {r}}_2\cdot \hat{\mathbf {r}}_2'), \end{aligned}$$

(107)

since $m_0^2 \delta _0+ m_0m_1(\delta _0+ \delta _1) + m_1^2 \delta _1= 0$.

Appendix 3: Averaged quantities

For completeness, we gather here the average formulae that are used in the computation of secular equations. Let $F(\mathbf {r},\dot{\mathbf {r}})$ be a function of a position vector $\mathbf {r}$ and velocity $\dot{\mathbf {r}}$, its averaged expression over the mean anomaly (M) is given by

$$\begin{aligned} \left\langle {F}\right\rangle _{M} = \frac{1}{2\pi }\int _0^{2\pi } F(\mathbf {r}, \dot{\mathbf {r}})\, \mathrm{d}M\ . \end{aligned}$$

(108)

Depending on the case, this integral is computing using the eccentric anomaly (E), or the true anomaly (v) as an intermediate variable. The basic formulae are

$$\begin{aligned} \mathrm{d}M= & {} \frac{r}{a}\mathrm{d}E = \frac{r^2}{a^2\sqrt{1-e^2}}\mathrm{d}v\ ,\nonumber \\ \mathbf {r}= & {} a(\cos E-e)\, \hat{\mathbf {e}} + a\sqrt{1-e^2}(\sin E)\, \hat{\mathbf {k}} \times \hat{\mathbf {e}}\ ,\nonumber \\ \mathbf {r}= & {} r\cos v\, \hat{\mathbf {e}} + r\sin v\, \hat{\mathbf {k}} \times \hat{\mathbf {e}}\ ,\nonumber \\ \dot{\mathbf {r}}= & {} \frac{na}{\sqrt{1-e^2}}\, \hat{\mathbf {k}} \times (\hat{\mathbf {r}} + \mathbf {e})\ ,\nonumber \\ r= & {} a (1-e\cos E) = \frac{a(1-e^2)}{1+e\cos v}\ , \end{aligned}$$

(109)

where $\hat{\mathbf {k}}$ is the unit vector of the orbital angular momentum, and $\mathbf {e}$ the Laplace–Runge–Lenz vector (Eq. 6). We have then

$$\begin{aligned} \left\langle {\frac{1}{r^3}}\right\rangle = \frac{1}{a^3(1-e^2)^{3/2}}\ , \quad \mathrm{and } \quad \left\langle {\frac{\mathbf {r} {}{\mathbf {r}}^t}{r^5}}\right\rangle = \frac{1}{2a^3(1-e^2)^{3/2}} \left( 1-\hat{\mathbf {k}} {}{\hat{\mathbf {k}}}^t \right) , \end{aligned}$$

(110)

where ${}{\mathbf {u}}^t$ denotes the transpose of any vector $\mathbf {u}$. This leads to

$$\begin{aligned} \left\langle {\frac{1}{r^3}P_2(\hat{\mathbf {r}} \cdot \hat{\mathbf {u}})}\right\rangle = -\frac{1}{2a^3(1-e^2)^{3/2}} P_2(\hat{\mathbf {k}} \cdot \hat{\mathbf {u}})\ , \end{aligned}$$

(111)

for any unit vector $\hat{\mathbf {u}}$. In the same way,

$$\begin{aligned} \left\langle {r^2}\right\rangle = a^2\left( 1+\frac{3}{2}e^2\right) \ , \quad \mathrm{and } \quad \left\langle {\mathbf {r} {}{\mathbf {r}}^t}\right\rangle = a^2\frac{1-e^2}{2} \left( 1-\hat{\mathbf {k}} {}{\hat{\mathbf {k}}}^t\right) + \frac{5}{2} a^2 \mathbf {e} {}{\mathbf {e}}^t\ , \end{aligned}$$

(112)

give

$$\begin{aligned} \left\langle {r^2 P_2(\hat{\mathbf {r}} \cdot \hat{\mathbf {u}})}\right\rangle = -\frac{a^2}{2}\Big ((1-e^2)P_2(\hat{\mathbf {k}} \cdot \hat{\mathbf {u}}) - 5 e^2 P_2(\hat{\mathbf {e}} \cdot \hat{\mathbf {u}})\Big )\ . \end{aligned}$$

(113)

The other useful formulae are

$$\begin{aligned} \left\langle {\frac{1}{r^6}}\right\rangle= & {} \frac{1}{a^6} f_1(e)\ , \end{aligned}$$

(114)

$$\begin{aligned} \left\langle {\frac{1}{r^8}}\right\rangle= & {} \frac{1}{a^8\sqrt{1-e^2}} f_2(e)\ , \end{aligned}$$

(115)

$$\begin{aligned} \left\langle {\frac{\mathbf {r} {}{\mathbf {r}}^t}{r^8}}\right\rangle= & {} \frac{\sqrt{1-e^2}}{2a^6} f_4(e) \left( 1-\hat{\mathbf {k}} {}{\hat{\mathbf {k}}}^t\right) +\frac{6+e^2}{4a^6(1-e^2)^{9/2}} \mathbf {e} {}{\mathbf {e}}^t\ , \end{aligned}$$

(116)

$$\begin{aligned} \left\langle {\frac{\mathbf {r}}{r^8}}\right\rangle= & {} \frac{5}{2}\frac{1}{a^7\sqrt{1-e^2}}\, f_4(e) \mathbf {e}\ , \end{aligned}$$

(117)

$$\begin{aligned} \left\langle {\frac{\mathbf {r}}{r^{10}}}\right\rangle= & {} \frac{7}{2}\frac{1}{a^9(1-e^2)}\, f_5(e) \mathbf {e}\ , \end{aligned}$$

(118)

$$\begin{aligned} \left\langle {\frac{(\mathbf {r} \cdot \dot{\mathbf {r}}) \mathbf {r}}{r^{10}}}\right\rangle= & {} \frac{n}{2a^7 \sqrt{1-e^2}} f_5(e)\, \hat{\mathbf {k}} \times \mathbf {e}\ , \end{aligned}$$

(119)

where the $f_i(e)$ functions are given by expressions (46)–(50).

Finally, for the average over the argument of the pericenter ($\omega$), we can proceed in an identical manner:

$$\begin{aligned} \left\langle {\mathbf {e} {}{\mathbf {e}}^t}\right\rangle _\omega = \frac{1}{2 \pi } \int _0^{2 \pi } \mathbf {e} {}{\mathbf {e}}^t \, d \omega = \frac{e^2}{2} \left( 1 - \mathbf {k} {}{\mathbf {k}}^t \right) , \end{aligned}$$

(120)

which gives

$$\begin{aligned} \left\langle { \left( \mathbf {e} \cdot \hat{\mathbf {u}} \right) \mathbf {e}}\right\rangle _\omega = \frac{e^2}{2} \Big ( \hat{\mathbf {u}} - ( \mathbf {k} \cdot \hat{\mathbf {u}} ) \mathbf {k} \Big ). \end{aligned}$$

(121)