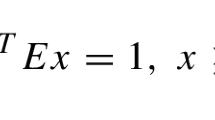Abstract
We consider an optimization problem with positively homogeneous functions in its objective and constraint functions. Examples of such positively homogeneous functions include the absolute value function and the p-norm function, where p is a positive real number. The problem, which is not necessarily convex, extends the absolute value optimization proposed in Mangasarian (Comput Optim Appl 36:43–53, 2007). In this work, we propose a dual formulation that, differently from the Lagrangian dual approach, has a closed-form and some interesting properties. In particular, we discuss the relation between the Lagrangian duality and the one proposed here, and give some sufficient conditions under which these dual problems coincide. Finally, we show that some well-known problems, e.g., sum of norms optimization and the group Lasso-type optimization problems, can be reformulated as positively homogeneous optimization problems.
Similar content being viewed by others
References
Alizadeh, F., Goldfarb, D.: Second-order cone programming. Math. Program. 95(1), 3–51 (2003)
Aravkin, A.Y., Burke, J.V., Drusvyatskiy, D., Friedlander, M.P., MacPhee, K.: Foundations of gauge and perspective duality. arXiv preprint arXiv:1702.08649 (2017)
Caccetta, L., Qu, B., Zhou, G.: A globally and quadratically convergent method for absolute value equations. Comput. Optim. Appl. 48(1), 45–58 (2011)
Chartrand, R.: Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 14(10), 707–710 (2007)
Chartrand, R., Yin, W.: Iteratively reweighted algorithms for compressive sensing. In: IEEE International Conference on Acoustics, Speech and Signal Processing, 2008. ICASSP 2008, IEEE, pp. 3869–3872 (2008)
Eldar, Y.C., Mishali, M.: Robust recovery of signals from a structured union of subspaces. IEEE Trans. Inf. Theory 55(11), 5302–5316 (2009)
Freund, R.M.: Dual gauge programs, with applications to quadratic programming and the minimum-norm problem. Math. Program. 38(1), 47–67 (1987)
Friedlander, M.P., Macedo, I., Pong, T.K.: Gauge optimization and duality. SIAM J. Optim. 24(4), 1999–2022 (2014)
Hu, S., Huang, Z.: A note on absolute value equations. Optim. Lett. 4(3), 417–424 (2010)
Hu, S., Huang, Z., Zhang, Q.: A generalized Newton method for absolute value equations associated with second order cones. J. Comput. Appl. Math. 235(5), 1490–1501 (2011)
Kirmaci, U.S., Bakula, M.K., Özdemir, M.E., Pecaric, J.E.: On some inequalities for \(p-\)norms. J. Inequal. Pure Appl. Math. 9(1), 1–8 (2008)
Luo, Z.Q., Pang, J.S., Ralph, D.: Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge (1996)
Mangasarian, O.L.: Absolute value equation solution via concave minimization. Optim. Lett. 1(1), 3–8 (2007)
Mangasarian, O.L.: Absolute value programming. Comput. Optim. Appl. 36(1), 43–53 (2007)
Mangasarian, O.L.: A generalized Newton method for absolute value equations. Optim. Lett. 3(1), 101–108 (2009)
Mangasarian, O.L., Meyer, R.R.: Absolute value equations. Linear Algebra Appl. 419(2), 359–367 (2006)
Meier, L., van de Geer, S., Bühlmann, P.: The group Lasso for logistic regression. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 70(1), 53–71 (2008)
Miao, X., Yang, J., Hu, S.: A generalized Newton method for absolute value equations associated with circular cones. Appl. Math. Comput. 269, 155–168 (2015)
Mourad, N., Reilly, J.P.: Minimizing nonconvex functions for sparse vector reconstruction. IEEE Trans. Signal Process. 58(7), 3485–3496 (2010)
Prokopyev, O.: On equivalent reformulations for absolute value equations. Comput. Optim. Appl. 44(3), 363–372 (2009)
Rohn, J.: A theorem of the alternatives for the equation \(ax+ b|x|= b\). Linear Multilinear Algebra 52(6), 421–426 (2004)
Rohn, J.: An algorithm for solving the absolute value equation. Electron. J. Linear Algebra 18(5), 589–599 (2009)
Stojnic, M., Parvaresh, F., Hassibi, B.: On the reconstruction of block-sparse signals with an optimal number of measurements. IEEE Trans. Signal Process. 57(8), 3075–3085 (2009)
Wolf, G.W.: Facility Location: Concepts, Models, Algorithms and Case Studies. Taylor & Francis, Routledge (2011)
Xue, G., Ye, Y.: An efficient algorithm for minimizing a sum of \(p-\)norms. SIAM J. Optim. 10(2), 551–579 (2000)
Yamanaka, S., Fukushima, M.: A branch-and-bound method for absolute value programs. Optimization 63(2), 305–319 (2014)
Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 68(1), 49–67 (2006)
Zhang, C., Wei, Q.J.: Global and finite convergence of a generalized Newton method for absolute value equations. J. Optim. Theory Appl. 143(2), 391–403 (2009)
Acknowledgements
The authors are grateful to Prof. Ellen. H. Fukuda for helpful comments and suggestions. This work was supported in part by a Grant-in-Aid for Scientific Research (C) (17K00032) from Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The following proposition shows that the dual of the p-norm function is the \(\infty \)-norm even when p is less than 1.
Proposition A.1
Suppose that \(p \in (0, 1)\). Then, the dual of the p-norm function is equal to the \(\infty \)-norm.
Proof
Let \(y \in \mathbb {R}^n\) be an arbitrary vector. If \(y = 0\), this proposition clearly holds. If \(y \ne 0\), from Definition 2.3, we obtain
Since \(p \in (0, 1)\), we note that \(\Vert x \Vert _1 \le \Vert x \Vert _p\) holds [11]. Then, we have
Now, take an arbitrary \(i_0 \in \mathop {\mathrm{argmax}}\limits _i | y_i |\), and define \(\bar{x}_i\) as follows:
where
Then, \(\Vert \bar{x} \Vert _p = 1\) and we have
which completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Yamanaka, S., Yamashita, N. Duality of nonconvex optimization with positively homogeneous functions. Comput Optim Appl 71, 435–456 (2018). https://doi.org/10.1007/s10589-018-0018-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-018-0018-y