Glorious pairs of roots and Abelian ideals of a Borel subalgebra

Abstract

Let ${{\mathfrak {g}}}$ be a simple Lie algebra with a Borel subalgebra ${{\mathfrak {b}}}$. Let $\Delta ^+$ be the corresponding (po)set of positive roots and $\theta$ the highest root. A pair $\{\eta ,\eta '\}\subset \Delta ^+$ is said to be glorious, if $\eta ,\eta '$ are incomparable and $\eta +\eta '=\theta$. Using the theory of abelian ideals of ${{\mathfrak {b}}}$, we (1) establish a relationship of $\eta ,\eta '$ to certain abelian ideals associated with long simple roots, (2) provide a natural bijection between the glorious pairs and the pairs of adjacent long simple roots (i.e., some edges of the Dynkin diagram), and (3) point out a simple transform connecting two glorious pairs corresponding to the incident edges in the Dynkin diagram. In types ${{\mathbf {\mathsf{{{DE}}}}}}_{}$, we prove that if $\{\eta ,\eta '\}$ corresponds to the edge through the branching node of the Dynkin diagram, then the meet $\eta \wedge \eta '$ is the unique maximal non-commutative root. There is also an analogue of this property for all other types except type ${{\mathbf {\mathsf{{{A}}}}}}_{}$. As an application, we describe the minimal non-abelian ideals of ${{\mathfrak {b}}}$.

1 Introduction

Let ${{\mathfrak {g}}}$ be a complex simple Lie algebra, with a Cartan subalgebra ${{\mathfrak {t}}}$ and a triangular decomposition ${{\mathfrak {g}}}={{\mathfrak {u}}}\oplus {{\mathfrak {t}}}\oplus {{\mathfrak {u}}}^-$. Here ${{\mathfrak {b}}}={{\mathfrak {u}}}\oplus {{\mathfrak {t}}}$ is a fixed Borel subalgebra. In this note, we present new combinatorial properties of root systems and abelian ideals of ${{\mathfrak {b}}}$. Our setting is always combinatorial, i.e., the abelian ideals of ${{\mathfrak {b}}}$, which are sums of root spaces of ${{\mathfrak {u}}}$, are identified with the corresponding sets of positive roots.

Let $\Delta$ be the root system of $({{\mathfrak {g}}},{{\mathfrak {t}}})$ in the ${{\mathbb {R}}}$-vector space $V={{\mathfrak {t}}}_{{\mathbb {R}}}^*$, $\Delta ^+$ the set of positive roots in $\Delta$ corresponding to ${{\mathfrak {u}}}$, $\Pi$ the set of simple roots in $\Delta ^+$, and $\theta$ the highest root in $\Delta ^+$. We regard $\Delta ^+$ as poset with the usual partial ordering ‘$\succcurlyeq$’. An ideal of $(\Delta ^+,\succcurlyeq )$ is a subset $I\subset \Delta ^+$ such that if $\gamma \in I, \nu \in \Delta ^+$, and $\nu +\gamma \in \Delta ^+$, then $\nu +\gamma \in I$. The set of minimal elements of I is denoted by $\min (I)$. Write also $\max (\Delta ^+\setminus I)$ for the set of maximal elements of $\Delta ^+\setminus I$. An ideal I is abelian, if $\gamma '+\gamma ''\not \in \Delta ^+$ for all $\gamma ',\gamma ''\in I$.

Let $\mathfrak {Ad}$ (resp. $\mathfrak {Ab}$) be the set of all (resp. all abelian) ideals of $\Delta ^+$. Then $\mathfrak {Ab}\subset \mathfrak {Ad}$ and we think of both sets as posets with respect to inclusion. The ideal generated by $\gamma \in \Delta ^+$ is $I\langle {\succcurlyeq }\gamma \rangle =\{\nu \in \Delta ^+\mid \nu \succcurlyeq \gamma \}\in \mathfrak {Ad}$, and $\gamma$ is said to be commutative, if $I\langle {\succcurlyeq }\gamma \rangle \in \mathfrak {Ab}$. Write $\Delta ^+_{\textsf {com}}$ for the set of all commutative roots. For any $\Delta$, this subset is explicitly described in [10, Theorem 4.4]. Note that $\Delta ^+_{\textsf {com}}\in \mathfrak {Ad}$.

A pair $\{\eta ,\eta '\}\subset \Delta ^+$ is said to be glorious, if $\eta ,\eta '$ are incomparable in the poset $(\Delta ^+,\succcurlyeq )$, i.e., $\{\eta ,\eta '\}$ is an antichain, and $\eta +\eta '=\theta$. Our goal is to explore properties of glorious pairs in connection with the theory of abelian ideals. We prove that

• (1) these $\eta , \eta '$ are necessarily long and commutative;

• (2) there is a natural bijection between the glorious pairs and the pairs of adjacent long simple roots, i.e., certain edges of the Dynkin diagram, see Theorem 3.5;

• (3) there is a simple transformation connecting two glorious pairs corresponding to a triple of consecutive long simple roots, i.e., two incident edges, see Theorem 3.11.

• (4) if $I\in \mathfrak {Ad}$ and $\#I {<} h^*$, where $h^*$ is the dual Coxeter number of $\Delta$, then $I\in \mathfrak {Ab}$, see Lemma . A weaker result that I is abelian if $\#I={\mathsf {rk\,}}{{\mathfrak {g}}}$ appears in [8, Lemma 12].

Let $\Pi _l$ be the set of long simple roots. (In the ${{\mathbf {\mathsf{{{ADE}}}}}}_{}$-case, all roots are assumed to be long and hence $\Pi _l=\Pi$.) Since $\Pi _l$ is connected in the Dynkin diagram, we have $\#\{\text {glorious pairs}\}=\#\Pi _l-1$, and the above bijection (2) can be understood as a bijection with the edges of the subdiagram $\Pi _l$. In the non-simply laced case, there is a unique pair of adjacent simple roots of different length. This gives rise to a similar pair of roots (the semi-glorious pair), which is discussed in Sect. 4.2. To state more properties of glorious pairs, we need more notation.

Let $\mathfrak {Ab}^o$ be the set of nonempty abelian ideals and $\Delta ^+_l$ the set of long positive roots. In [9, Sect. 2], we constructed a map $\tau : \mathfrak {Ab}^o\rightarrow \Delta ^+_l$, which is onto (see Sect. 1). If $\tau (I)=\mu$, then $\mu \in \Delta ^+_l$ is called the rootlet of I, also denoted ${\mathsf {rt}}(I)$. Letting $\mathfrak {Ab}_\mu =\tau ^{-1}(\mu )$, we get a partition of $\mathfrak {Ab}^o$ parameterised by $\Delta ^+_l$. Each $\mathfrak {Ab}_\mu$ is a subposet of $\mathfrak {Ab}$ and, moreover, $\mathfrak {Ab}_\mu$ has a unique minimal and unique maximal element (ideal) [9, Sect. 3]. These extreme elements of $\mathfrak {Ab}_\mu$ are denoted by $I(\mu )_{\textsf {min}}$ and $I(\mu )_{\textsf {max}}$.

• We show that the glorious pairs are related to the abelian ideals $I(\alpha )_{\textsf {min}}$ with $\alpha \in \Pi _l$. If a glorious pair $\{\eta ,\eta '\}$ gives rise to adjacent $\alpha ,\alpha '\in \Pi _l$, then $\eta \in \min (I(\alpha )_{\textsf {min}})$, $\eta '\in \min (I(\alpha ')_{\textsf {min}})$ and also ${\mathsf {cl}}(\eta )=\alpha '$ and ${\mathsf {cl}}(\eta ')=\alpha$, see Proposition 3.2. Here ${\mathsf {cl}}({\cdot })$ is a natural map from $\Delta ^+_{\textsf {com}}$ to ${\widehat{\Pi }}$, the set of affine simple roots, see Sect. 1 for details.

• Conversely, given adjacent $\alpha ,\alpha '\in \Pi _l$, the corresponding glorious pair is the unique pair in $I(\alpha )_{\textsf {min}}\cup I(\alpha ')_{\textsf {min}}$ that sums to $\theta$. The constructions of $\{\eta ,\eta '\}$ from $\{\alpha ,\alpha '\}$ and vice versa heavily rely on properties of $I(\alpha )_{\textsf {min}}$, $I(\alpha )_{\textsf {max}}$, and the minuscule elements of the affine Weyl group ${\widehat{W}}$, as it was developed in [9, 11].

• It is noticed in [10, Sect. 4] and conceptually proved in [14, Sect. 3] that if $\Delta$ is not of type ${{\mathbf {\mathsf{{{A}}}}}}_{n}$, then $\Delta ^+_{\textsf {nc}}:=\Delta ^+\setminus \Delta ^+_{\textsf {com}}$ has a unique maximal element, denoted ${\lfloor \theta /2\rfloor }$. Then ${\lceil \theta /2\rceil }:=\theta -{\lfloor \theta /2\rfloor }\in \Delta ^+$ and ${\lfloor \theta /2\rfloor }\preccurlyeq {\lceil \theta /2\rceil }$. In Sect. 4, we prove that if $\Delta \in \{{{\mathbf {\mathsf{{{D-E}}}}}}_{}\}$, then the interval $[{\lfloor \theta /2\rfloor },{\lceil \theta /2\rceil }]$ in $\Delta ^+$, which is a cube ${\mathbb {B}}^3$ [14, Sect. 5], is related to the glorious pairs associated with the edges through the branching node, $\varvec{{\hat{\alpha }}}$, of the Dynkin diagram. This is deduced from some properties of the shortest element of W that takes $\theta$ to $\varvec{{\hat{\alpha }}}$, see Theorem 4.3. If $\Delta \in \{{{\mathbf {\mathsf{{{B-C-F-G}}}}}}_{}\}$, then ${\lceil \theta /2\rceil }={\lfloor \theta /2\rfloor }\in \Pi$ and $\{{\lfloor \theta /2\rfloor }, {\lceil \theta /2\rceil }\}$ is just the unique semi-glorious pair associated with the adjacent simple roots of different length.

• In Sect. 5, we prove that all minimal non-abelian ideals of ${{\mathfrak {b}}}$ are related to either the glorious or semi-glorious pairs. All these ideals have the same cardinality, $h^*$.

We refer to [1, 5, § 3.1] for standard results on root systems and Weyl groups. The numbering of simple roots for the exceptional Lie algebras follows [5, Tables].

2 Preliminaries

Our main objects are $\Pi =\{\alpha _1,\dots ,\alpha _n\}$, the vector space $V=\oplus _{i=1}^n{{\mathbb {R}}}\alpha _i$, the Weyl group W generated by simple reflections $s_\alpha$ ($\alpha \in \Pi$), and a W-invariant inner product $(\ ,\ )$ on V. Set $\rho =\frac{1}{2}\sum _{\nu \in \Delta ^+}\nu$. The partial ordering ‘$\preccurlyeq$’ in $\Delta ^+$ is defined by the rule that $\mu \preccurlyeq \nu$ if $\nu -\mu$ is a non-negative integral linear combination of simple roots. If $\mu =\sum _{i=1}^n c_i\alpha _i\in \Delta ^+$, then ${\mathsf {ht}}(\mu ):=\sum _{i=1}^n c_i$ and $\{\mu :\alpha _i\}:=c_i$.

1.1 The theory of abelian ideals of ${{\mathfrak {b}}}$ is built on their relationship, due to D. Peterson, with the minuscule elements of the affine Weyl group ${\widehat{W}}$, see Kostant’s account in [6]; another approach is presented in [2]. Recall the necessary setup. Letting ${\widehat{V}}=V\oplus {{\mathbb {R}}}\delta \oplus {{\mathbb {R}}}\lambda$, we extend the inner product $(\ ,\ )$ on ${\widehat{V}}$ so that $(\delta ,V)=(\lambda ,V)=(\delta ,\delta )= (\lambda ,\lambda )=0$ and $(\delta ,\lambda )=1$. Set $\alpha _0=\delta -\theta$, where $\theta$ is the highest root in $\Delta ^+$. Then

• ${\widehat{\Delta }}=\{\Delta +k\delta \mid k\in {{\mathbb {Z}}}\}$ is the set of affine (real) roots;

• ${\widehat{\Delta }}^+= \Delta ^+ \cup \{ \Delta +k\delta \mid k\geqslant 1\}$ is the set of positive affine roots;

• ${\widehat{\Pi }}=\Pi \cup \{\alpha _0\}$ is the corresponding set of affine simple roots;

• $\mu ^\vee =2\mu /(\mu ,\mu )$ is the coroot corresponding to $\mu \in {\widehat{\Delta }}$;

For each $\alpha \in {\widehat{\Pi }}$, let $s_\alpha$ denote the corresponding reflection in $GL({\widehat{V}})$.That is, $s_\alpha (x)=x- (x,\alpha )\alpha ^\vee$ for any $x\in {\widehat{V}}$. The affine Weyl group, ${\widehat{W}}$, is the subgroup of $GL({\widehat{V}})$ generated by the reflections $s_\alpha$ ($\alpha \in {\widehat{\Pi }}$). The extended inner product $(\ ,\ )$ on ${\widehat{V}}$ is ${\widehat{W}}$-invariant. The inversion set of $w\in {\widehat{W}}$ is $\mathcal {N}(w)=\{\nu \in {\widehat{\Delta }}^+\mid w(\nu )\in -{\widehat{\Delta }}^+\}$.

1.2 Following D. Peterson, we say that ${\hat{w}}\in {\widehat{W}}$ is minuscule, if $\mathcal {N}({\hat{w}})=\{\delta -\gamma \mid \gamma \in I_{{\hat{w}}}\}$ for some $I_{{\hat{w}}}\subset \Delta$, see [6, 2.2]. One then proves that (i) $I_{{\hat{w}}}\subset \Delta ^+$ and it is an abelian ideal, (ii) the assignment ${\hat{w}}\mapsto I_{{\hat{w}}}$ yields a bijection between the minuscule elements of ${\widehat{W}}$ and the abelian ideals, see [6, 2, Proposition 2.8]. Accordingly, if $I\in \mathfrak {Ab}$, then ${\hat{w}}_I$ denotes the corresponding minuscule element of ${\widehat{W}}$. Obviously, $\# I=\#\mathcal {N}({\hat{w}}_I)=\ell ({\hat{w}}_I)$, where $\ell$ is the usual length function on ${\widehat{W}}$.

Proposition 1.1

(cf. [9, Theorems 2.2& 2.4]) Let $J\in \mathfrak {Ab}$.

• 1) For $\gamma \in J$, we have $\gamma \in \min (J)$ if and only if ${\hat{w}}_J(\delta -\gamma )\in -{\widehat{\Pi }}$;

• 2) if $\eta \not \in J$, then $J\cup \{\eta \} \in \mathfrak {Ab}$ if and only if ${\hat{w}}_J(\delta -\gamma )=:\beta \in {\widehat{\Pi }}$. If this is the case, then ${\hat{w}}_{J\cup \{\gamma \}}=s_\beta {\hat{w}}_J$.

1.3 Using the above assertion, one defines a natural map ${\mathsf {cl}}: \Delta ^+_{\textsf {com}}\rightarrow {\widehat{\Pi }}$ as follows. Given $\gamma \in \Delta ^+_{\textsf {com}}$, take any $I\in \mathfrak {Ab}$ such that $\gamma \in \min (I)$. (For instance, $I=I\langle {\succcurlyeq }\gamma \rangle$ will do.) Then ${\hat{w}}_I(-\delta +\gamma )=\beta \in {\widehat{\Pi }}$ and we set ${\mathsf {cl}}(\gamma )=\beta$. The point is that this $\beta$ does not depend on the choice of I, see [10, Theorem 4.5]. We say that ${\mathsf {cl}}(\gamma )$ is the class of $\gamma$. It can be shown that ${\mathsf {cl}}(\gamma )\in \Pi$, whenever $\gamma \in {\mathcal {H}}\setminus \{\theta \}$.

1.4 For any nontrivial minuscule ${\hat{w}}_I$, we have ${\hat{w}}_I(\alpha _0)+\delta ={\hat{w}}_I(2\delta -\theta )\in \Delta ^+_l$ [9, Proposition 2.5]. This yields the mapping $\tau : \mathfrak {Ab}^o\rightarrow \Delta ^+_l$, which is onto [9, Theorem 2.6(1)]. That is, ${\mathsf {rt}}(I)={\hat{w}}_I(2\delta -\theta )$. The Heisenberg ideal

$$\begin{aligned} {\mathcal {H}}:=\{\gamma \in \Delta ^+ \mid (\gamma , \theta )\ne 0\}= \{\gamma \in \Delta ^+ \mid (\gamma , \theta )> 0\}\in \mathfrak {Ad}\end{aligned}$$

plays a prominent role in the theory of abelian ideals and posets $\mathfrak {Ab}_\mu =\tau ^{-1}(\mu )$:

• $I=I(\mu )_{\textsf {min}}$ for some $\mu \in \Delta ^+_l$ if and only if $I\subset {\mathcal {H}}$ [9, Theorem 4.3];

• $\# I(\mu )_{\textsf {min}}=(\rho ,\theta ^\vee -\mu ^\vee )+1$ [9, Theorem 4.2(4)];

• For $I\in \mathfrak {Ab}^o$, we have $I\in \mathfrak {Ab}_\mu$ if and only if $I\cap {\mathcal {H}}=I(\mu )_{\textsf {min}}$ [11, Proposition 3.2];

If $I=I(\mu )_{\textsf {min}}$, then ${\hat{w}}_I$ has the following simple description. First, there is a unique element of minimal length in W that takes $\theta$ to $\mu$ [9, Theorem 4.1]. Writing $w_\mu$ for this element, one has $\ell (w_\mu )=(\rho ,\theta ^\vee -\mu ^\vee )$ and ${\hat{w}}_I=w_\mu s_{\alpha _0}$ [9, Theorem 4.2].

1.5 Generalizing Peterson’s idea, Cellini–Papi associate a canonical element of ${\widehat{W}}$ to any $I\in \mathfrak {Ad}$, see [2, Sect. 2]. Set $I^k:=I^{k-1}+I$ for $k\geqslant 2$, where $J+I=\{\nu +\eta \in \Delta ^+\mid \nu \in J, \eta \in I\}$. If $m\in {{\mathbb {N}}}$ is the smallest integer such that $I^m=\varnothing$, then ${\hat{w}}_I$ is the unique element of ${\widehat{W}}$ such that ${\mathcal {N}}({\hat{w}}_I)=\bigsqcup _{k=1}^{m-1} (k\delta -I^k)$. For the abelian ideals, $I^2=\varnothing$ and one recovers the definition of minuscule elements.

Some basic results on abelian ideals of ${{\mathfrak {b}}}$ that explore other directions of investigations can be found in [3, 4, 7, 13, 15].

3 Some auxiliary results

We begin with some properties of arbitrary ideals in $(\Delta ^+,\preccurlyeq )$. Recall that $\#{\mathcal {H}}=2h^*-3$, where $h^*:=(\rho , \theta ^\vee )+1$ is the dual Coxeter number of $\Delta$.

Lemma 2.1

If $I\subset \Delta ^+$ is a non-abelian ideal, then there are $\gamma _1,\gamma _2\in I$ such that $\gamma _1+\gamma _2=\theta$.

Proof

If $\gamma _1+\gamma _2=\mu$ for some $\gamma _1,\gamma _2\in I$ and $\mu \ne \theta$, then there is $\alpha \in \Pi$ such that $\mu +\alpha$ is a root. In this case, $\gamma _1+\alpha$ or $\gamma _2+\alpha$ is a root, necessarily in I, which provides an induction step. $\square$

Lemma 2.2

If ${\hat{I}}\in \mathfrak {Ad}$ is non-abelian, then $\# {\hat{I}}\geqslant h^*$. Conversely, if $I\subset {\mathcal {H}}$ is an ideal and $\# I\geqslant h^*$, then I is not abelian.

Proof

• 1) If ${\hat{I}}$ is non-abelian, then so is ${\hat{I}}\cap {\mathcal {H}}$ (Lemma 2.1). Therefore, we may assume that ${\hat{I}}\subset {\mathcal {H}}$ and $\gamma _1+\gamma _2=\theta$ for some $\gamma _1,\gamma _2\in {\hat{I}}$. Let ${\hat{w}}_{{\hat{I}}} \in {\widehat{W}}$ be the canonical element associated with ${\hat{I}}$, see Sect. 1.5. Since ${\hat{I}}^2=\{\theta \}$ and ${\hat{I}}^3=\varnothing$, we have

  $$\begin{aligned} {\mathcal {N}}({\hat{w}}_{{\hat{I}}})=\{\delta -\gamma \mid \gamma \in {\hat{I}}\}\cup \{2\delta -\theta \} . \end{aligned}$$

  Since ${\widehat{\Delta }}^+\setminus {\mathcal {N}}({\hat{w}}_{{\hat{I}}})$ is a closed under addition subset of ${\widehat{\Delta }}^+$, ${\mathcal {H}}\setminus {\hat{I}}$ does not contain pairs of summable (to $\theta$) elements. Hence ${\mathcal {H}}\setminus {\hat{I}}$ is contained in a Lagrangian half of ${\mathcal {H}}\setminus \{\theta \}$ and is strictly less (because ${\hat{I}}$ contains a summable pair $\gamma _1,\gamma _2$). Thus,

  $$\begin{aligned} \#({\mathcal {H}}\setminus {\hat{I}})=\#{\mathcal {H}}- \# {\hat{I}}< (\#{\mathcal {H}}-1)/2 . \end{aligned}$$

  Hence $\# {\hat{I}}> (\#{\mathcal {H}}+1)/2=h^*-1$.

• 2) The set ${\mathcal {H}}\setminus \{\theta \}$ consists of $h^*-2$ different pairs of roots that sums to $\theta$. Therefore, if $\# I\geqslant h^*$, then I contains at least one such summable pair. $\square$

Remark 2.3

(1) :

A weaker result that all ${{\mathfrak {b}}}$-ideals of dimension ${\mathsf {rk\,}}{{\mathfrak {g}}}$ are abelian appears in [8, Lemma 12]. (Note that $h^*$ can be much larger than ${\mathsf {rk\,}}{{\mathfrak {g}}}$.)

(2) :

Of course, there are abelian ideals I with $\#I \geqslant h^*$. Such ideals are not contained in ${\mathcal {H}}$.

Lemma 2.4

If $I\subset {\mathcal {H}}$ is an abelian ideal and $I\cup \{\gamma \}$ is a non-abelian ideal for some $\gamma \in \Delta ^+$, then (i) $\gamma \in {\mathcal {H}}$, (ii) $I=I(\alpha )_{\textsf {min}}$ for some $\alpha \in \Pi _l$, and (iii) $\#I=h^*-1$.

Proof

Since I is abelian, whereas $I\cup \{\gamma \}$ is not, there is $\mu \in I$ such that $\gamma +\mu =\theta$ (use Lemma 2.1). Hence $\gamma \in {\mathcal {H}}$. By [9, Proposition 4.2(4)], if I is abelian, then $\#I \leqslant (\rho ,\theta ^\vee )=h^*-1$. Furthermore, $\#I=h^*-1$ if and only if $I=I(\alpha )_{\textsf {min}}$ for some $\alpha \in \Pi$. Now, since $I\cup \{\gamma \}$ is non-abelian, we have $\#(I\cup \{\gamma \})\geqslant h^*$. Thus, $\#I=h^*-1$ and we are done. $\square$

If $\eta +\eta '=\theta$, then we set ${\tilde{I}}=I\langle {\succcurlyeq } \eta ,\eta '\rangle = \{\nu \in \Delta ^+\mid \nu \succcurlyeq \eta \text { or } \nu \succcurlyeq \eta '\}$. Then ${\tilde{I}}$ is not abelian and $\min ({\tilde{I}})\subset \{\eta ,\eta '\}$. Clearly, both roots $\eta ,\eta '$ are either long or short.

Lemma 2.5

If $\eta ,\eta '\in \Delta ^+_{\textsf {com}}$ and $\eta +\eta '=\theta$, then

(i):

these two roots are incomparable and hence $\min ({\tilde{I}})= \{\eta ,\eta '\}$;

(ii):

the ideals ${\tilde{I}}\setminus \{\eta \}$ and ${\tilde{I}}\setminus \{\eta '\}$ are abelian;

(iii):

$\eta ,\eta '\in \Delta _l$.

Proof

(i) :

Obvious.

(ii) :

Assume that ${\tilde{I}}\setminus \{\eta \}$ is non-abelian. Then there are $\gamma _1,\gamma _2\in {\tilde{I}}\setminus \{\eta \}$ such that $\gamma _1+\gamma _2=\theta$. Since both $I\langle {\succcurlyeq }\eta \rangle$ and $I\langle {\succcurlyeq }\eta '\rangle$ are abelian, up to permutation of indices, one has

$$\begin{aligned} \gamma _1\in I\langle {\succcurlyeq }\eta '\rangle \text { and }\gamma _2\in I\langle {\succcurlyeq }\eta \rangle \setminus \{\eta \}, \\ \text { while } \gamma _1\not \in I\langle {\succcurlyeq }\eta \rangle \text { and } \gamma _2\not \in I\langle {\succcurlyeq }\eta '\rangle . \end{aligned}$$

This means that ${\mathsf {ht}}(\gamma _1)\geqslant {\mathsf {ht}}(\eta ')$ and ${\mathsf {ht}}(\gamma _2)> {\mathsf {ht}}(\eta )$. Hence ${\mathsf {ht}}(\gamma _1+\gamma _2)>{\mathsf {ht}}(\theta )$. A contradiction! Therefore, ${\tilde{I}}\setminus \{\eta \}\in \mathfrak {Ab}$ and likewise for ${\tilde{I}}\setminus \{\eta '\}$.

(iii) :

Now, $J={\tilde{I}}\setminus \{\eta ,\eta '\}$ is an abelian ideal that has two abelian extensions: $J \mapsto J\cup \{\eta \}$, $J \mapsto J\cup \{\eta '\}$. Let ${\hat{w}}_J\in {\widehat{W}}$ be the minuscule element corresponding to J. The first extension means that ${\hat{w}}_J(\delta -\eta )=\beta$ for some $\beta \in {\widehat{\Pi }}$. Likewise, ${\hat{w}}_J(\delta -\eta ')=\beta '\in {\widehat{\Pi }}$, see Proposition 1.1. Since $\eta +\eta '=\theta$, we have ${\hat{w}}_J(2\delta -\theta )={\hat{w}}_J(2\delta -\eta -\eta ')=\beta +\beta '$. On the other hand, ${\hat{w}}_J(2\delta -\theta )=\tau (J)$, and it is an element of $\Delta ^+_l$, see Sect. 1.4. Hence $\beta ,\beta '$ are adjacent simple roots of $\Delta$. Finally, because $\theta$ is long, then so is $\beta +\beta '$. This is only possible if $\beta ,\beta '$ are long and hence $\eta ,\eta '$ are also long. $\square$

Remark

All the ideals $I(\alpha )_{\textsf {min}}$ ($\alpha \in \Pi _l$) have the same cardinality, $h^*-1=(\rho ,\theta ^\vee )$; while this is not the case for $I(\alpha )_{\textsf {max}}$. A general formula for $\#(I(\alpha )_{\textsf {max}})$ is given in [3].

4 Glorious pairs, adjacent long simple roots and incident edges of the Dynkin diagram

Definition 1

A pair $\{\eta ,\eta '\}\subset \Delta ^+$ is said to be glorious, if these two roots are incomparable and $\eta +\eta '=\theta$.

Set ${\lfloor \theta /2\rfloor }=\sum _{\alpha \in \Pi } \lfloor \{\theta :\alpha \}/2\rfloor \alpha$. If $\Delta$ is of type ${{\mathbf {\mathsf{{{A}}}}}}_{n}$, then ${\lfloor \theta /2\rfloor }=0$. For all other types, one can prove uniformly that ${\lfloor \theta /2\rfloor }\in \Delta ^+$, ${\lfloor \theta /2\rfloor }$ is not commutative, and ${\lfloor \theta /2\rfloor }$ is the unique maximal element of $\Delta ^+_{\textsf {nc}}:=\Delta ^+\setminus \Delta ^+_{\textsf {com}}$, see [14, Sect. 3].

Lemma 3.1

Suppose that $\eta +\eta '=\theta$. Then $\eta ,\eta '$ are incomparable $\Leftrightarrow$ they are commutative.

Proof

The implication ‘$\Leftarrow$’ is obvious (cf. Lemma 2.5(i)). To prove the other implication, assume that $\eta \not \in \Delta ^+_{\textsf {com}}$. Then there are $\gamma _1,\gamma _2\succcurlyeq \eta$ such that $\gamma _1+\gamma _2=\theta$. Therefore, $\theta \succcurlyeq 2\eta$. In other words, $\eta \preccurlyeq {\lfloor \theta /2\rfloor }$. This clearly implies that $\eta '\succcurlyeq {\lfloor \theta /2\rfloor }$ and hence $\eta '\succcurlyeq {\lfloor \theta /2\rfloor }\succcurlyeq \eta$. $\square$

Note that both elements of a glorious pair belong to ${\mathcal {H}}$ and they are long in view of Lemma 2.5(iii).

4.1 From glorious pairs to adjacent simple roots

Proposition 3.2

For a glorious pair $\{\eta ,\eta '\}$ and ${\tilde{I}}=I\langle {\succcurlyeq } \eta ,\eta '\rangle$ as in Sect. 2, we have

(i):

$\#{\tilde{I}}=h^*$ and ${\tilde{I}}=I(\alpha )_{\textsf {min}}\cup \{\eta '\}=I(\alpha ')_{\textsf {min}}\cup \{\eta \}$ for some $\alpha , \alpha '\in \Pi _l$;

(ii):

the long simple roots $\alpha , \alpha '$ are adjacent in the Dynkin diagram;

(iii):

${\mathsf {cl}}(\eta )=\alpha '$ and ${\mathsf {cl}}(\eta ')=\alpha$;

(iv):

$\eta \in \min (I(\alpha )_{\textsf {min}})$ and $\eta '\in \min (I(\alpha ')_{\textsf {min}})$.

Proof

(i) :

This follows from Lemmata 2.4 and 2.5(ii).

(ii) :

Using $J:={\tilde{I}}\setminus \{\eta ,\eta '\}$, the minuscule element ${\hat{w}}_J\in {\widehat{W}}$, and two abelian extensions of J, as in the proof of Lemma 2.5(iii), we obtain

$$\begin{aligned} {\hat{w}}_J(\delta -\eta )=\beta \in \Pi _l, \ {\hat{w}}_J(\delta -\eta ')=\beta '\in \Pi _l, \text { and } {\mathsf {rt}}(J)=\beta +\beta '. \end{aligned}$$

This also means that ${\hat{w}}_{J\cup \{\eta \}}=s_{\beta }{\hat{w}}_J$ and ${\hat{w}}_{J\cup \{\eta '\}}=s_{\beta '}{\hat{w}}_J$, see Proposition 1.1. Then

$$\begin{aligned} \alpha ={\mathsf {rt}}(I(\alpha )_{\textsf {min}})={\mathsf {rt}}(J\cup \{\eta \})=s_{\beta }{\hat{w}}_J(2\delta - \theta )=s_\beta (\beta +\beta ')=\beta ', \\ \alpha ' ={\mathsf {rt}}(I(\alpha ')_{\textsf {min}})={\mathsf {rt}}(J\cup \{\eta '\})=s_{\beta '}{\hat{w}}_J(2\delta - \theta )=s_{\beta '}(\beta +\beta ')=\beta . \end{aligned}$$

(iii) :

By the previous part of the proof, we have ${\hat{w}}_{J\cup \{\eta \}}=s_{\alpha '}{\hat{w}}_J$ and ${\hat{w}}_{J\cup \{\eta '\}}=s_{\alpha }{\hat{w}}_J$, and by definition of the class we have

$$\begin{aligned} {\mathsf {cl}}(\eta )=-s_{\alpha '}{\hat{w}}_J(\delta -\eta )=-s_{\alpha '}(\alpha ')=\alpha ', \\ {\mathsf {cl}}(\eta ')=-s_{\alpha }{\hat{w}}_J(\delta -\eta ')=-s_{\alpha }(\alpha )=\alpha . \end{aligned}$$

(iv) :

This follows from (i).

$\square$

Remark

Part (ii) of the proposition already appears in [9, Proposition 3.4(1)]. However, we essentially reproduced a proof in order to have the necessary notation for Part (iii).

It follows from Proposition 3.2 that one associates an edge of the Dynkin (sub-)diagram of $\Pi _l$ to any glorious pair. Below, we prove that this map is actually a bijection and obtain some more properties for the quadruple $(\eta ,\eta ',\alpha ,\alpha ')$ of Proposition 3.2. To achieve this goal, one should be able to construct a glorious pair starting from a pair of adjacent long simple roots.

4.2 From adjacent simple roots to glorious pairs

Let $\alpha \in \Pi _l$. By [9, Proposition 4.6], there is a natural bijection between $\min (I(\alpha )_{\textsf {min}})$ and the simple roots adjacent to $\alpha$, and this correspondence respects the length. More precisely, let $w_\alpha \in W$ be the unique shortest element taking $\theta$ to $\alpha$. If $\alpha '\in \Pi$ is adjacent to $\alpha$, then $\eta :=w_\alpha ^{-1}(\alpha +\alpha ')\in \min (I(\alpha )_{\textsf {min}})$ corresponds to $\alpha '$. In particular, $\eta \in \Delta ^+_{\textsf {com}}$. (Here $\alpha '$ is not necessarily long and $\Vert \alpha '\Vert =\Vert \eta \Vert$.) Suppose now that $\alpha '$ is long. Then so is $\eta$. Furthermore, $(\theta ,\eta )=(\alpha ,\alpha +\alpha ')>0$, hence $\eta ':=\theta -\eta$ is a long root, too.

Proposition 3.3

If $\alpha ,\alpha '\in \Pi _l$ are adjacent and $\eta =w_\alpha ^{-1}(\alpha +\alpha ')$, then $\eta '=w_{\alpha '}^{-1}(\alpha +\alpha ')$ has the property that $\eta +\eta '=\theta$. Furthermore, ${\mathsf {cl}}(\eta )=\alpha '$ and ${\mathsf {cl}}(\eta ')=\alpha$.

Proof

• 1) Recall that $\ell (w_{\alpha +\alpha '})=(\rho ,\theta ^\vee -(\alpha +\alpha ')^\vee )=h^*-3$, see Sect. 1.4. Then $\ell (s_\alpha w_{\alpha +\alpha '})\leqslant h^*-2=(\rho ,\theta ^\vee -(\alpha ')^\vee )$ and $s_\alpha w_{\alpha +\alpha '}$ takes $\theta$ to $\alpha '$. Hence one must have $w_{\alpha '}=s_{\alpha }w_{\alpha +\alpha '}$ and also $w_\alpha =s_{\alpha '}w_{\alpha +\alpha '}$. (The first equality means that a “shortest reflection route” inside $\Delta ^+_l$ from $\theta$ to $\alpha '$ can be realized as a shortest route from $\theta$ to $\alpha +\alpha '$ and then the last step $\alpha +\alpha '{\mathop {\longrightarrow }\limits ^{s_\alpha }} \alpha '$.) Now $w_\alpha ^{-1}(\alpha +\alpha ')=w_{\alpha +\alpha '}^{-1}(\alpha ')$. Hence $w_\alpha ^{-1}(\alpha +\alpha ')+w_{\alpha '}^{-1}(\alpha +\alpha ')=w_{\alpha +\alpha '}^{-1}(\alpha '+\alpha )=\theta$.

• 2) To compute the class, we need the fact that the minuscule element of $I(\alpha )_{\textsf {min}}$ in ${\widehat{W}}$ is $w_\alpha s_{\alpha _0}$. (This element already appeared in Sect. 3.1 as $s_{\alpha '}{\hat{w}}_J$, which is the same, because ${\hat{w}}_J=w_{\alpha +\alpha '}s_{\alpha _0}$ and $s_{\alpha '}w_{\alpha +\alpha '}=w_{\alpha }$.) Therefore, by definition,

  $$\begin{aligned} {\mathsf {cl}}(\eta )=-w_\alpha s_{\alpha _0}(\delta -\eta )=-w_\alpha (\theta -\eta )=-\alpha +(\alpha +\alpha ')=\alpha ' . \end{aligned}$$

  (3.1)

  And likewise for $\eta '$. $\square$

Thus, both $\eta$ and $\eta '$ are long, commutative and sum to $\theta$, i.e., we have obtained a glorious pair associated with $(\alpha ,\alpha ')$. The above result shows that the construction of $\eta$ and $\eta '$ is symmetric w.r.t. $\alpha$ and $\alpha '$, and the classes of $\eta$ and $\eta '$ are computable.

Remark 3.4

Proposition 3.3 provides an explicit formula for $\eta ,\eta '$ via adjacent $\alpha ,\alpha '\in \Pi _l$. There is also another approach. By [9, Theorem 2.1], for two adjacent long simple roots, $I(\alpha )_{\textsf {min}}\cap I(\alpha ')_{\textsf {min}}=I(\alpha +\alpha ')_{\textsf {min}}$. Furthermore, $\# I(\alpha +\alpha ')_{\textsf {min}}=(\rho , \theta ^\vee -(\alpha +\alpha ')^\vee )+1=h^*-2$, see Sect. 1.4. Therefore, $\#\bigl (I(\alpha )_{\textsf {min}}\setminus I(\alpha +\alpha ')_{\textsf {min}}\bigr )=1$ and likewise for $\alpha '$. Hence $I(\alpha )_{\textsf {min}}\setminus I(\alpha +\alpha ')_{\textsf {min}}=\{\eta \}$ and $I(\alpha ')_{\textsf {min}}\setminus I(\alpha +\alpha ')_{\textsf {min}}=\{\eta '\}$. Since $\#\bigl ( I(\alpha )_{\textsf {min}}\cup I(\alpha ')_{\textsf {min}}\bigr )=h^*$ and $I(\alpha )_{\textsf {min}}\cup I(\alpha ')_{\textsf {min}}\subset {\mathcal {H}}$, this ideal cannot be abelian, i.e., $\{\eta ,\eta '\}$ is a glorious pair.

4.3 Bijections and examples

It is easily seen that the constructions of Sects. 3.1 and 3.2 are mutually inverse. This yields one of the main results of the article.

Theorem 3.5

There is a natural bijection

$$\begin{aligned} \{ \text {the glorious pairs in } \ \Delta ^+\} {\mathop {\longleftrightarrow }\limits ^{1:1}} \{ \text {the pairs of adjacent roots in } \Pi _l\}, \\ (\eta ,\eta ') {\mathop {\longmapsto }\limits ^{1:1}} (\alpha ,\alpha ') \end{aligned}$$

such that $\eta \in \min (I(\alpha )_{\textsf {min}})$, $\eta '\in \min (I(\alpha ')_{\textsf {min}})$, ${\mathsf {cl}}(\eta )=\alpha '$, and ${\mathsf {cl}}(\eta ')=\alpha$.

Corollary 3.6

The number of glorious pairs equals $\#\Pi _l-1$.

This provides an a priori proof for Theorem 4.8(ii) in [12], where glorious pairs appear disguised as “summable 2-antichains” in $\Delta (1):={\mathcal {H}}\setminus \{\theta \}$.

Corollary 3.7

Every ordered glorious pair $(\eta ,\eta ')$ arises as an element of the set $\min (I(\alpha )_{\textsf {min}})\times \max (\Delta ^+\setminus I(\alpha )_{\textsf {max}})$ for a unique $\alpha \in \Pi _l$.

Proof

Given a glorious pair $(\eta ,\eta ')\in \min (I(\alpha )_{\textsf {min}})\times \min (I(\alpha ')_{\textsf {min}})$, one can apply [11, Theorem 4.7] in two different ways. For, one can say that either $\eta '=\theta -\eta \in \max (\Delta ^+\setminus I(\alpha )_{\textsf {max}})$ or $\eta =\theta -\eta '\in \max (\Delta ^+\setminus I(\alpha ')_{\textsf {max}})$. Therefore,

$$\begin{aligned} (\eta ,\eta ')\in \min (I(\alpha )_{\textsf {min}})\times \max (\Delta ^+\setminus I(\alpha )_{\textsf {max}}) , \\ (\eta ',\eta )\in \min (I(\alpha ')_{\textsf {min}})\times \max (\Delta ^+\setminus I(\alpha ')_{\textsf {max}}) . \end{aligned}$$

Example 3.8

Let $\Delta$ be of type ${{\mathbf {\mathsf{{{D}}}}}}_{n}$, with $\alpha _i=\varepsilon _i-\varepsilon _{i+1}$ ($1\leqslant i\leqslant n-1$) and $\alpha _n=\varepsilon _{n-1}+\varepsilon _n$. Then $\theta =\varepsilon _1+\varepsilon _2$ and the quadruples $(\alpha ,\alpha ',\eta ,\eta ')$ are given in the table.

Using these data, one easily determines $\min (I(\alpha )_{\textsf {min}})$ for all $\alpha \in \Pi$. Given $\alpha _i\in \Pi$, we look at all its occurrences in the first two columns an pick the related roots $\eta$, if $\alpha _i=\alpha$, and $\eta '$, if $\alpha _i=\alpha '$. This yields $\min (I(\alpha _i)_{\textsf {min}})$. For instance, $\min (I(\alpha _{n-2})_{\textsf {min}})=\{\varepsilon _2+\varepsilon _{n-1}, \varepsilon _1+\varepsilon _{n},\varepsilon _1-\varepsilon _{n}\}$.

Example 3.9

Let $\Delta$ be of type ${{\mathbf {\mathsf{{{B}}}}}}_{n}$, with $\alpha _i=\varepsilon _i-\varepsilon _{i+1}$ ($1\leqslant i\leqslant n$), where $\varepsilon _{n+1}=0$. Then $\Pi _l=\{\alpha _1,\dots ,\alpha _{n-1}\}$, $\theta =\varepsilon _1+\varepsilon _2$, and the quadruples $(\alpha ,\alpha ',\eta ,\eta ')$ are

Example 3.10

In the following table, we illustrate the bijection of Theorem 3.5 and Corollary 3.7 with data for $\Delta$ of type ${{\mathbf {\mathsf{{{E}}}}}}_{6}$. The second column contains 10 different roots, which form 5 glorious pairs. For each root there, one has to pick the unique root such that their sum equals $\theta =\left( \begin{array}{c} 12321\\ 2\\ \end{array}\right)$. The same 10 roots occur in the third column, and reading the table along the rows, we meet all 10 ordered glorious pairs.

Remark

There are no glorious pairs for ${{\mathbf {\mathsf{{{C}}}}}}_{n}$ and ${{\mathbf {\mathsf{{{G}}}}}}_{2}$, since $\#\Pi _l=1$ in these cases.

4.4 Adjacent glorious pairs

Two glorious pairs are said to be adjacent if the corresponding edges are incident in the Dynkin diagram, i.e., have a common node (in $\Pi _l$). Here we prove that there is a simple transform connecting two adjacent glorious pairs. First, we need some notation.

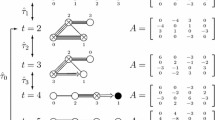
Let $\alpha _i,\alpha _j,\alpha _k$ be consecutive long simple roots in the Dynkin diagram, see figure

It is not forbidden here that one of the nodes is the branching node (if there is any).

To handle this situation, we slightly modify our notation. The glorious pair associated with $(\alpha _i,\alpha _j)$ is denoted by $(\eta _{ij}, \eta _{ji})$ and likewise for $(\alpha _j,\alpha _k)$. Here $\eta _{ij}\in \min (I(\alpha _i)_{\textsf {min}})$, ${\mathsf {cl}}(\eta _{ij})=\alpha _j$, etc. Set $w_i=w_{\alpha _i}$, the shortest element of W taking $\theta$ to $\alpha _i$, and likewise for the other admissible sets of indices, e.g., $w_{jk}$ (resp. $w_{ijk}$) is the shortest element taking $\theta$ to $\alpha _j+\alpha _k$ (resp. $\alpha _i+\alpha _j+\alpha _k$). Then $\eta _{ij}=w_i^{-1}(\alpha _i+\alpha _j)$ and $\eta _{ji}=w_j^{-1}(\alpha _i+\alpha _j)$, cf. Sect. 3.2.

Theorem 3.11

If $\alpha _i,\alpha _j,\alpha _k$ are consecutive long simple roots, then

$$\begin{aligned} (\eta _{jk},\eta _{kj})=(\eta _{ij}-\gamma , \eta _{ji}+\gamma ) , \end{aligned}$$

where $\gamma =w_{ijk}^{-1}(\alpha _j)\in \Pi _l$ and $(\gamma ,\theta )=0$.

Proof

It is easily seen that $w_i=s_js_kw_{ijk}, \ w_j=(s_is_k)w_{ijk}, \ w_k=s_js_i w_{ijk}$, cf. the proof of Proposition 3.3(1). Then

$$\begin{aligned} \eta _{jk}= & {} w_j^{-1}(\alpha _j+\alpha _k)=w_{ijk}^{-1}(s_ks_i)(\alpha _j +\alpha _k)=w_{ijk}^{-1}(\alpha _i+\alpha _j) , \\ \eta _{kj}= & {} w_k^{-1}(\alpha _j+\alpha _k)=w_{ijk}^{-1}{\cdot }s_i s_j(\alpha _j+\alpha _k)=w_{ijk}^{-1}(\alpha _k) . \end{aligned}$$

Similarly, $\eta _{ij}=w_{ijk}^{-1}(\alpha _i)$ and $\eta _{ji}=w_{ijk}^{-1}(\alpha _j+\alpha _k)$. Therefore

$$\begin{aligned} \eta _{jk}-\eta _{ij}=w_{ijk}^{-1}(\alpha _j)=\eta _{ji}-\eta _{kj} . \end{aligned}$$

(3.2)

Since $(\alpha _i+\alpha _j+\alpha _k,\alpha _j)=0$, it follows from [13, Lemma 2.1] that $w_{ijk}^{-1}(\alpha _j)\in \Pi$ and $(w_{ijk}^{-1}(\alpha _j),\theta )=0$. $\square$

We will say that this $\gamma \in \Pi$ is the transition root for two incident edges $(\alpha _i,\alpha _j)$ and $(\alpha _j,\alpha _k)$. If there is a longer chain of long simple roots, say

then one obtains two associated transition roots $\gamma _j=w_{ijk}^{-1}(\alpha _j)$ and $\gamma _k=w_{jkl}^{-1}(\alpha _k)$. A useful complement to the previous theorem is

Proposition 3.12

The simple roots $\gamma _j, \gamma _k$ are adjacent in the Dynkin diagram, i.e., $(\gamma _j,\gamma _k)<0$, and $\eta _{kl}-\eta _{ij}=\gamma _j+\gamma _k=\eta _{ji}-\eta _{lk} \in \Delta ^+$.

Proof

Using the obvious notation, one has $w_{ijk}=s_l w_{ijkl}$ and $w_{jkl}=s_i w_{ijkl}$. Therefore $\gamma _j=w_{ijk}^{-1}(\alpha _j)=w_{ijkl}^{-1}(\alpha _j)$ and $\gamma _k=w_{jkl}^{-1}(\alpha _k)=w_{ijkl}^{-1}(\alpha _k)$. Hence $(\gamma _j,\gamma _k)=(\alpha _j,\alpha _k)<0$. To prove the second relation, use Eq. (3.2) and its analogue for (jkl). $\square$

Remark 3.13

For a chain of m consecutive long simple roots, say $\alpha _1,\dots ,\alpha _m$, one similarly obtains $m-2$ transition roots $\gamma _j$, $j=2,\dots ,m-1$. Here $\gamma _2=w_{123}^{-1}(\alpha _2)$, etc. It follows from Proposition 3.12 that $\gamma _i$ and $\gamma _{i+1}$ are adjacent in the Dynkin diagram. Moreover, arguing by induction on $m\geqslant 4$, one easily proves that all $\gamma _i$’s are different, i.e., they form a genuine chain in $\Pi$. This provides a curious bijection in the ${{\mathbf {\mathsf{{{ADE}}}}}}_{}$-case. Namely, Theorem 3.11 asserts that each pair of incident edges in the Dynkin diagram defines a $\gamma \in \Pi _l$ such that $(\gamma ,\theta )=0$. For ${{\mathbf {\mathsf{{{D}}}}}}_{n}$ and ${{\mathbf {\mathsf{{{E}}}}}}_{n}$, there is $n-1$ pair of incident edges in the Dynkin diagram and also $n-1$ simple roots orthogonal to $\theta$. For ${{\mathbf {\mathsf{{{A}}}}}}_{n}$, the same phenomenon occurs with $n-2$ in place of $n-1$. Thus, one obtains natural bijections related to the Dynkin diagram:

$$\begin{aligned} \left\{ \!\!\begin{array}{c} \text {triples of consecutive} \\ \text {simple roots} \end{array}\!\! \right\} \leftrightarrow \{\text {pairs of incident edges}\}\leftrightarrow \{\gamma \in \Pi \mid (\gamma ,\theta )=0\} . \end{aligned}$$

That is, every simple root orthogonal to $\theta$ occurs as the transition root for a unique pair of incident edges. In Sect. 3, we provide this correspondence for ${{\mathbf {\mathsf{{{E}}}}}}_{6}$, ${{\mathbf {\mathsf{{{E}}}}}}_{7}$, ${{\mathbf {\mathsf{{{E}}}}}}_{8}$, and ${{\mathbf {\mathsf{{{D}}}}}}_{8}$.

This fails, however, in the non-simply laced case.

5 Glorious pairs related to the interval $[{\lfloor \theta /2\rfloor },{\lceil \theta /2\rceil }]$, tails, and elements of W

Recall that ${\lfloor \theta /2\rfloor }=\sum _{\alpha \in \Pi } \lfloor \{\theta :\alpha \}/2\rfloor \alpha$ and if $\Delta \ne {{\mathbf {\mathsf{{{A}}}}}}_{n}$, then ${\lfloor \theta /2\rfloor }\in \Delta ^+$. Outside type ${{\mathbf {\mathsf{{{A}}}}}}_{}$, $\theta$ is a multiple of a fundamental weight and there is a unique $\alpha _\theta \in \Pi$ such that $(\theta ,\alpha _\theta )\ne 0$. Here $\{\theta :\alpha _\theta \}=2$, hence $\{{\lfloor \theta /2\rfloor }:\alpha _\theta \}=1$ and ${\lfloor \theta /2\rfloor }\in {\mathcal {H}}$. Then ${\lceil \theta /2\rceil }:=\theta -{\lfloor \theta /2\rfloor }$ also belongs to ${\mathcal {H}}$ and ${\lfloor \theta /2\rfloor }\preccurlyeq {\lceil \theta /2\rceil }$. Set ${\mathfrak {J}}=\{\gamma \in \Delta ^+\mid {\lfloor \theta /2\rfloor }\preccurlyeq \gamma \preccurlyeq {\lceil \theta /2\rceil }\}$. By [14, Sect. 5], if $\Delta \in \{{{\mathbf {\mathsf{{{D-E}}}}}}_{}\}$, then ${\mathfrak {J}}\simeq {\mathbb {B}}^3$ (Boolean cube, see Fig. 2); and if $\Delta \in \{{{\mathbf {\mathsf{{{B-C-F-G}}}}}}_{}\}$, then ${\mathfrak {J}}=\{{\lfloor \theta /2\rfloor },{\lceil \theta /2\rceil }\}$.

Write |M| for the sum of elements of a subset $M\subset \Pi$. Recall that $|M|\in \Delta ^+$ if and only if M is connected. Our results below exploit the following fact for $\Delta$ that is not of type ${{\mathbf {\mathsf{{{A}}}}}}_{}$ (see [14, Proposition 4.6]):

$$\begin{aligned} \text { there is a unique }\varvec{{\hat{\alpha }}}\in \Pi \text { such that }|\Pi _l|+\varvec{{\hat{\alpha }}}\in \Delta ^+\text { and then }w_{|\Pi _l|}^{-1}(\varvec{{\hat{\alpha }}})=-{\lfloor \theta /2\rfloor }. \end{aligned}$$

(4.1)

Set $\mathcal {O}=\{\alpha \in \Pi \mid \{\theta :\alpha \} \text { is odd}\}$. The roots in $\mathcal {O}$ are also said to be odd. It follows from the definition of ${\lfloor \theta /2\rfloor }$ that

$$\begin{aligned} \theta -2{\lfloor \theta /2\rfloor }= {\lceil \theta /2\rceil }-{\lfloor \theta /2\rfloor }=|\mathcal {O}| . \end{aligned}$$

(4.2)

5.1 The glorious pairs related to ${\mathfrak {J}}$ in the $\{{{\mathbf {\mathsf{{{D-E}}}}}}_{}\}$-case

In types ${{\mathbf {\mathsf{{{D}}}}}}_{}$ and ${{\mathbf {\mathsf{{{E}}}}}}_{}$, there are exactly three odd roots. They are denoted by $\beta _1,\beta _2, \beta _3$. In this case, $\varvec{{\hat{\alpha }}}\in \Pi$ of Eq. (4.1) is the branching node in the Dynkin diagram and $\Pi \setminus \{\varvec{{\hat{\alpha }}}\}$ has three connected components, which are called tails. Each tail ${{\mathcal {T}}}_i$ is a chain, and it is also regarded as a subset of $\Pi$. Then $|{{\mathcal {T}}}_i|\in \Delta ^+$, $\Pi \setminus \{\varvec{{\hat{\alpha }}}\}=\sqcup _{i=1}^3 {{\mathcal {T}}}_i$, and

$$\begin{aligned} |\Pi |=\sum _{i=1}^3|{{\mathcal {T}}}_i|+\varvec{{\hat{\alpha }}}. \end{aligned}$$

(4.3)

Set ${\widehat{{{\mathcal {T}}}}}_i={{\mathcal {T}}}_i\cup \{\varvec{{\hat{\alpha }}}\}$. Then $|{\widehat{{{\mathcal {T}}}}}_i|\in \Delta ^+$ and $\Pi \setminus {\widehat{{{\mathcal {T}}}}}_i$ is a disconnected subset of the Dynkin diagram. Therefore, $|\Pi |-|{\widehat{{{\mathcal {T}}}}}_i|\not \in \Delta ^+$ and hence $(|\Pi |,|{\widehat{{{\mathcal {T}}}}}_i|^\vee )\geqslant 0$. Since ${\mathcal {N}}(w_\mu ^{-1})=\{\gamma \in \Delta ^+\mid (\gamma ,\mu ^\vee )=-1\}$ for any $\mu \in \Delta ^+_l$ [9, Theorem 4.1], this means that $|{\widehat{{{\mathcal {T}}}}}_i|\not \in {\mathcal {N}}(w_{|\Pi |}^{-1})$, i.e., $w_{|\Pi |}^{-1}(|{\widehat{{{\mathcal {T}}}}}_i|)\in \Delta ^+$. Moreover, the following is true.

Theorem 4.1

After a suitable renumbering of the $\beta _i$’s, one has

$$\begin{aligned} w_{|\Pi |}^{-1}(|{\widehat{{{\mathcal {T}}}}}_i|)=\beta _i \quad \text {for } \ i=1,2,3 . \end{aligned}$$

Proof

It follows from Eq. (4.3) that $|\Pi |=\sum _{i=1}^3|{\widehat{{{\mathcal {T}}}}}_i|-2\varvec{{\hat{\alpha }}}$. By (4.1), we also have $w_{|\Pi |}^{-1}(\varvec{{\hat{\alpha }}})=-{\lfloor \theta /2\rfloor }$. Therefore,

$$\begin{aligned} \theta =w_{|\Pi |}^{-1}(|\Pi |)=\sum _{i=1}^3 w_{|\Pi |}^{-1}(|{\widehat{{{\mathcal {T}}}}}_i|)+2{\lfloor \theta /2\rfloor }. \end{aligned}$$

Using Eq. (4.2), we obtain $\beta _1+\beta _2+\beta _3=\sum _{i=1}^3 w_{|\Pi |}^{-1}(|{\widehat{{{\mathcal {T}}}}}_i|)$, and each summand in the right-hand side is a positive root. Hence the assertion! $\square$

Corollary 4.2

$w_{|\Pi |}^{-1}(|{{\mathcal {T}}}_i|)={\lfloor \theta /2\rfloor }+\beta _i$.

It is assumed below that numbering of the tails and odd roots is matched as prescribed by Theorem 4.1. The explicit correspondence ${{\mathcal {T}}}_i\longleftrightarrow \beta _i$ is pointed out in Sect. 2.

Theorem 4.3

Let $\nu _i\in {{\mathcal {T}}}_i$ be the unique root adjacent to $\varvec{{\hat{\alpha }}}$. Then $w_{\varvec{{\hat{\alpha }}}}^{-1}(\nu _i){=-}{\lfloor \theta /2\rfloor }{-}\beta _i$.

Proof

For each tail ${{\mathcal {T}}}_i$, we define the element $w({{\mathcal {T}}}_i)\in W$ as the ordered product of simple reflections $s_\alpha$, where the $\alpha$’s are taken along the chain ${{\mathcal {T}}}_i$ and $s_{\nu _i}$ is the initial factor on the left, see Fig. 1.

Fig. 1

Tails

Note that $w({{\mathcal {T}}}_i)$ and $w({{\mathcal {T}}}_j)$ commute, $w({{\mathcal {T}}}_i)^{-1}(\nu _i)=-|{{\mathcal {T}}}_i|$, and $w({{\mathcal {T}}}_j)^{-1}(\nu _i)=\nu _i$ if $i\ne j$. We can write $w_{\varvec{{\hat{\alpha }}}}=w({{\mathcal {T}}}_1)\,w({{\mathcal {T}}}_2)\,w({{\mathcal {T}}}_3)\,w_{|\Pi |}$. Indeed, $w({{\mathcal {T}}}_i)|\Pi |=|\Pi |-|{{\mathcal {T}}}_i|$ and hence the element in the RHS takes $\theta$ to $|\Pi |-\sum _{i=1}^3 |{{\mathcal {T}}}_i|= \varvec{{\hat{\alpha }}}$. Moreover, its length is at most $(\rho ,\theta ^\vee )-1=(\rho ,\theta ^\vee -\varvec{{\hat{\alpha }}}^\vee )$. Hence it must be the unique element of minimal length taking $\theta$ to $\varvec{{\hat{\alpha }}}$. Then

$$\begin{aligned} w_{\varvec{{\hat{\alpha }}}}^{-1}(\nu _i)=w_{|\Pi |}^{-1} \prod _{j=1}^3w({{\mathcal {T}}}_j)^{-1}(\nu _i)=w_{|\Pi |}^{-1}w({{\mathcal {T}}}_i)^{-1}(\nu _i)= w_{|\Pi |}^{-1}(-|{{\mathcal {T}}}_i|)=-{\lfloor \theta /2\rfloor }-\beta _i . \end{aligned}$$

We assume below that $\{i,j,k\}=\{1,2,3\}$.

Corollary 4.4

For any $i\in \{1,2,3\}$,

(i):

$w_{\varvec{{\hat{\alpha }}}}^{-1}(\varvec{{\hat{\alpha }}}+\nu _i)={\lceil \theta /2\rceil }-\beta _i={\lfloor \theta /2\rfloor }+\beta _j+\beta _k$;

(ii):

$w_{\nu _i}^{-1}(\varvec{{\hat{\alpha }}}+\nu _i)={\lfloor \theta /2\rfloor }+\beta _i$.

Proof

(i) :

Use the equality $w_{\varvec{{\hat{\alpha }}}}^{-1}(\varvec{{\hat{\alpha }}})=\theta$.

(ii) :

This follows from (i) and Proposition 3.3 with $\alpha =\varvec{{\hat{\alpha }}}$ and $\alpha '=\nu _i$. $\square$

It follows that the six roots strictly between ${\lfloor \theta /2\rfloor }$ and ${\lceil \theta /2\rceil }$ form the three glorious pairs corresponding to the edges of the Dynkin diagram through $\varvec{{\hat{\alpha }}}$. Namely,

By [11, Appendix], the join ‘$\vee$’ of two elements of the poset $(\Delta ^+,\succcurlyeq )$ always exists. In [14, Sect. 2], we proved that the meet ‘$\wedge$’ of two elements of $(\Delta ^+,\succcurlyeq )$ exists if and only if their supports are not disjoint. More precisely, if ${\mathsf {supp}}(\eta ): =\{\alpha \in \Pi \mid \{\eta :\alpha \}\ne 0\}$ and ${\mathsf {supp}}(\eta )\cap {\mathsf {supp}}(\eta ')\ne \varnothing$, then

$$\begin{aligned} \eta \wedge \eta '=\sum _{\alpha \in \Pi } \min \{\{\eta :\alpha \},\{\eta ':\alpha \}\}\alpha . \end{aligned}$$

In this case, $\eta \vee \eta '=\sum _{\alpha \in \Pi } \max \{\{\eta :\alpha \},\{\eta ':\alpha \}\}\alpha$. Hence $\eta +\eta '=\eta \wedge \eta '+\eta \vee \eta '$. Therefore, for any glorious pair, we have $\eta \wedge \eta '+\eta \vee \eta '=\theta$.

Corollary 4.5

If $\{\eta ,\eta '\}$ is the glorious pair corresponding to $\{\varvec{{\hat{\alpha }}},\nu _i\}$, then $\eta \wedge \eta '={\lfloor \theta /2\rfloor }$ and $\eta \vee \eta '={\lceil \theta /2\rceil }$.

Proof

$({\lfloor \theta /2\rfloor }+\beta _i)\wedge ({\lfloor \theta /2\rfloor }+\beta _j+\beta _k)={\lfloor \theta /2\rfloor }$ and $({\lceil \theta /2\rceil }-\beta _j-\beta _k)\vee ({\lceil \theta /2\rceil }-\beta _i)={\lceil \theta /2\rceil }$. $\square$

Remark 4.6

For any glorious pair $\{\eta ,\eta '\}$, the meet $\eta \wedge \eta '$ exists and belongs to ${\mathcal {H}}$ whenever $\Delta$ is not of type ${{\mathbf {\mathsf{{{A}}}}}}_{n}$, see [14, Remark 2.6]. Since $\eta ,\eta '\in I\langle {\succcurlyeq } (\eta \wedge \eta ')\rangle$, we have $\eta \wedge \eta '\in \Delta ^+_{\textsf {nc}}$ and hence $\eta \wedge \eta '\preccurlyeq {\lfloor \theta /2\rfloor }$. It is just proved that this upper bound is attained for the edges through the branching node $\varvec{{\hat{\alpha }}}\in \Pi$. Using Theorem 3.11, Proposition 3.12, and Remark 3.13, one can prove that, for all other edges, the strict inequality $\eta \wedge \eta '\prec {\lfloor \theta /2\rfloor }$ holds. More precisely, let us say that the edges through $\varvec{{\hat{\alpha }}}$ are central. For any other edge $\mathcal {E}$ of the subdiagram $\Pi _l$, we consider the natural distance, $d(\mathcal {E})$, from $\mathcal {E}$ to the closest central edge. (That is, $d(\mathcal {E})=1$ if $\mathcal {E}$ is not central, but is incident to a central edge, etc.) Suppose that $\{\eta ,\eta '\}$ corresponds to $\mathcal {E}$ and

$$\begin{aligned} \mathcal {E}=\mathcal {E}_0, \mathcal {E}_1,\dots , \mathcal {E}_d=\mathcal {C} , \end{aligned}$$

is the unique chain of edges connecting $\mathcal {E}$ with the closest central edge $\mathcal {C}$.

Let $\gamma _i$ be the transition root for the incident edges $(\mathcal {E}_{i-1},\mathcal {E}_i)$, $i=1,\dots ,d$, cf. Theorem 3.11. Then $d=d(\mathcal {E})$ and $\eta \wedge \eta '={\lfloor \theta /2\rfloor }-\sum _{i=1}^d \gamma _i$, hence $\eta \vee \eta '={\lceil \theta /2\rceil }+\sum _{i=1}^d \gamma _i$. In particular, ${\mathsf {ht}}(\eta \wedge \eta ')={\mathsf {ht}}({\lfloor \theta /2\rfloor })-d(\mathcal {E})$.

Fig. 2

The interval between ${\lfloor \theta /2\rfloor }$ and ${\lceil \theta /2\rceil }$ for ${{\mathbf {\mathsf{{{D}}}}}}_{n}$ and ${{\mathbf {\mathsf{{{E}}}}}}_{n}$

Remark 4.7

If $\{i,j,k\}=\{1,2,3\}$, then the odd root $\beta _i$ is the transition root between the pair of central edges $\{\varvec{{\hat{\alpha }}},\nu _j\}$ and $\{\varvec{{\hat{\alpha }}},\nu _k\}$.

All the roots but ${\lfloor \theta /2\rfloor }$ in Fig. 2 are commutative, hence their classes are well-defined.

Proposition 4.8

We have ${\mathsf {cl}}({\lfloor \theta /2\rfloor }+\beta _i)=\varvec{{\hat{\alpha }}}$, ${\mathsf {cl}}({\lfloor \theta /2\rfloor }+\beta _j+\beta _k)=\nu _i$, and ${\mathsf {cl}}({\lceil \theta /2\rceil })=\varvec{{\hat{\alpha }}}$.

Proof

Since the roots between ${\lfloor \theta /2\rfloor }$ and ${\lceil \theta /2\rceil }$ comprise three glorious pairs, the first two equalities follow from Proposition 3.3 and Corollary 4.4.

The root ${\lceil \theta /2\rceil }$ is adjacent to the roots ${\lceil \theta /2\rceil }-\beta _i$ ($i=1,2,3$) in the Hasse diagram of $\Delta ^+$, see Fig. 2. Therefore, ${\mathsf {cl}}({\lceil \theta /2\rceil })$ is adjacent to the ${\mathsf {cl}}({\lceil \theta /2\rceil }-\beta _i)=\nu _i$ ($i=1,2,3$) in the Dynkin diagram, see [10, Lemma 4.6]. Hence the only possibility for ${\mathsf {cl}}({\lceil \theta /2\rceil })$ is $\varvec{{\hat{\alpha }}}$. $\square$

Remark

The roots of class $\varvec{{\hat{\alpha }}}$ are colored in Fig. 2.

5.2 The interval ${\mathfrak {J}}$ in the $\{{{\mathbf {\mathsf{{{B-C-F-G}}}}}}_{}\}$-case

The construction in Sect. 3.2 associates a glorious pair to any pair of adjacent long simple roots. This leaves nothing more to say in the simply laced case. But, in the non-simply laced cases, there is exactly one pair of adjacent simple roots of different length, and one can construct a certain pair of roots as follows.

Let $\alpha \in \Pi _l$, $\alpha '\in \Pi _s:=\Pi \setminus \Pi _l$, and $(\alpha ,\alpha ')<0$. Then $\alpha '=\varvec{{\hat{\alpha }}}$ and $\eta =w_\alpha ^{-1}(\alpha +\alpha ')\in \min (I(\alpha )_{\textsf {min}})$ is a short root in ${\mathcal {H}}$. Hence $\eta \in \Delta ^+_{\textsf {com}}$ and $(\eta ,\theta )=(\alpha ,\alpha +\alpha ')>0$. But $\eta '=\theta -\eta \not \in \Delta ^+_{\textsf {com}}$ in view of Lemma 2.5(iii). For this reason, we say that the pair $(\eta ,\eta ')$ is the (unique) semi-glorious pair.

Theorem 4.9

Suppose that $\Delta$ is non-simply laced and $(\eta ,\eta ')$ is the semi-glorious pair associated with the adjacent $\alpha \in \Pi _l$ and $\alpha '\in \Pi _s$, as above. Then

(i):

$I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}=I(\alpha )_{\textsf {min}}$ and $\eta -\eta '\in \Pi$;

(ii):

${\mathsf {cl}}(\eta )=\alpha '$;

(iii):

$(\eta ,\eta ')=({\lceil \theta /2\rceil },{\lfloor \theta /2\rfloor })$.

Proof

(i) :

Since $I\langle {\succcurlyeq }\eta '\rangle$ is not abelian, there are $\mu ,\mu '\succcurlyeq \eta$ such that $\mu +\mu '=\theta$ (Lemma 2.1). Because $\eta \in \min (I(\alpha )_{\textsf {min}})$, it follows from [11, Theorem 4.7] that $\eta '=\theta -\eta \in \max (\Delta ^+\setminus I(\alpha )_{\textsf {max}})$. Hence $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}$ lies in $I(\alpha )_{\textsf {max}}$ and thereby is abelian. Therefore, the only possibility is $\mu =\eta$, $\mu '=\eta '$. In this case, we have $\eta '\prec \eta$.

Furthermore, since $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}$ is abelian, while $I\langle {\succcurlyeq }\eta '\rangle$ is not, Lemma 2.4 implies that the former ideal is $I(\beta )_{\textsf {min}}$ for some $\beta \in \Pi _l$. By the construction, $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\} \subset I(\alpha )_{\textsf {max}}$. Now, using the theory developed in [11, Sect. 3], we obtain

$$\begin{aligned} I(\alpha )_{\textsf {min}}=\bigl ( I(\alpha )_{\textsf {max}}\cap {\mathcal {H}}\bigr ) \supset \bigl ( I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}\bigr )=I(\beta )_{\textsf {min}} , \end{aligned}$$

which implies that $\beta =\alpha$. Thus, $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}=I(\alpha )_{\textsf {min}}$ contains $\eta$ as a minimal element. Since all minimal elements of $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}$ cover $\eta '$, we have $\eta -\eta '\in \Pi$.

(ii) :

The computation of Eq. (3.1) applies here as well.

(iii) :

Set $\gamma =|\Pi _l|$, the sum of all roots in $\Pi _l$. Then $\gamma \in \Delta ^+$ and also $\gamma +\alpha '\in \Delta ^+$. That is, $\alpha '=\varvec{{\hat{\alpha }}}$ occurs in Eq. (4.1). Therefore, $w_\gamma ^{-1}(\alpha ')=-{\lfloor \theta /2\rfloor }$. Let ${{\mathcal {T}}}$ be the connected component of $\Pi \setminus \{\alpha \}$ that contains long roots. Then ${{\mathcal {T}}}$ is a chain, and if ${{\mathcal {T}}}$ consists of consecutive (long) simple roots $\alpha _{i_1}, \dots , \alpha _{i_s}$, where $\alpha _{i_s}$ is adjacent to $\alpha$, then we consider the element ${\varvec{w}}=s_{i_s}\cdots s_{i_1}w_\gamma \in W$. Since $w_\gamma (\theta )=\gamma = \alpha _{i_1}+ \dots +\alpha _{i_s}+\alpha$, we have ${\varvec{w}}(\theta )=\alpha$. Because $\ell ({\varvec{w}})\leqslant \ell (w_\gamma )+ \#(\Pi _l)-1=(\rho ,\theta ^\vee )-1$, we see that $\ell ({\varvec{w}})=(\rho ,\theta ^\vee )-1$ and ${\varvec{w}}=w_\alpha$. Since $s_{i_j}(\alpha ')=\alpha '$ for each $i_j$, we have $w_\alpha ^{-1}(\alpha ')=w_\gamma ^{-1}(\alpha ')=-{\lfloor \theta /2\rfloor }$. Therefore, $\eta =w_\alpha ^{-1}(\alpha +\alpha ')=\theta -{\lfloor \theta /2\rfloor }={\lceil \theta /2\rceil }$. $\square$

The complete information on the semi-glorious pairs is presented in the following table:

The numbering of simple roots follows [5, Tables], and the notation, say, (1221) stands for $\alpha _1+2\alpha _2+2\alpha _3+\alpha _4$, and so on.

Remark 4.10

Our result that ${\lceil \theta /2\rceil }-{\lfloor \theta /2\rfloor }\in \Pi$ yields a proof for the fact that $\#\mathcal {O}=1$ in the ${{\mathbf {\mathsf{{{BCFG}}}}}}_{}$-case, cf. Eq. (4.2).

There is an analogue of Theorem 3.11 that involves semi-glorious pairs. Let $\alpha _i,\alpha _j,\alpha _k$ be consecutive simple roots such that $\alpha _i,\alpha _j\in \Pi _l$ and $\alpha _k\in \Pi _s$, cf. Sect. 3.4. (This only happens for ${{\mathbf {\mathsf{{{B}}}}}}_{n}$ and ${{\mathbf {\mathsf{{{F}}}}}}_{4}$.) Then we still have the shortest elements $w_i$ and $w_j$, but not $w_k$. Recall that $\eta _{ij}=w_i^{-1}(\alpha _i+\alpha _j)$, $\eta _{ji}=w_j^{-1}(\alpha _i+\alpha _j)$, and also $\eta _{jk}=w_j^{-1}(\alpha _j+\alpha _k)$ is the commutative root in the semi-glorious pair. It follows from Theorem 4.9(iii) that $\eta _{jk}={\lceil \theta /2\rceil }$, but this is not needed now.

Theorem 4.11

$\eta _{jk}-\eta _{ij}=:\gamma$ is a short simple root and $(\gamma ,\theta )=0$.

Proof

In this situation, $\Vert \alpha _j\Vert ^2/\Vert \alpha _k\Vert ^2=2$ and therefore $\alpha _i+\alpha _j+2\alpha _k\in \Delta ^+_l$. Write $w_{ij\underline{k}}$ for the shortest element of W taking $\theta$ to $\alpha _i+\alpha _j+2\alpha _k$. Then $w_i=s_j s_k w_{ij\underline{k}}$ and $w_j=(s_is_k)w_{ij\underline{k}}$. Therefore

$$\begin{aligned} \eta _{jk}= & {} w_{ij\underline{k}}^{-1}(s_ks_i)(\alpha _j+\alpha _k)=w_{ij\underline{k}}^{-1}(\alpha _i+\alpha _j+\alpha _k), \\ \eta _{ij}= & {} w_{ij\underline{k}}^{-1}s_k s_j (\alpha _i+\alpha _j)= w_{ij\underline{k}}^{-1}(\alpha _i) . \end{aligned}$$

Hence $\eta _{jk}-\eta _{ij}=w_{ij\underline{k}}^{-1}(\alpha _j+\alpha _k)=\gamma$ is a short root. Here $(\gamma ,\theta )= (\alpha _i+\alpha _j+2\alpha _k, \alpha _j+\alpha _k)=0$, but we cannot blindly apply [13, Lemma 2.1], as in Theorem  3.11, because $\alpha _j+\alpha _k$ is not simple. Nevertheless, that proof can be adapted to this situation, see below. $\square$

Lemma 4.12

Under the above notation, $\gamma :=w_{ij\underline{k}}^{-1}(\alpha _j+\alpha _k)$ is a simple root.

Proof

Set $\mu =\alpha _i+\alpha _j+2\alpha _k$. Since $\mathcal {N}(w_{\mu }^{-1})=\{\nu \in \Delta ^+\mid (\nu ,\mu ^\vee )=-1\}$ [9, Theorem 4.1(2)] and $(\mu ,\alpha _j+\alpha _k)=0$, we have $\gamma \in \Delta ^+$. Assume that $w_{\mu }^{-1}(\alpha _j+\alpha _k)=\gamma _1+\gamma _2$ is a sum of positive roots. Then $\alpha _j+\alpha _k=w_\mu (\gamma _1)+w_\mu (\gamma _2)$.

If both summands in the RHS are positive, then $\alpha _j=w_\mu (\gamma _1)$, which is impossible, because $(\alpha _j,\mu ^\vee )=-1$ and hence $w_\mu ^{-1}(\alpha _j)$ is negative. Therefore, without loss of generality, one may assume that $-\nu _1:=w_\mu (\gamma _1)$ is negative. Then $\nu _1\in \mathcal {N}(w_\mu ^{-1})$, hence $(-\nu _1,\mu ^\vee )=1$. Consequently, $(\gamma _1,\theta ^\vee )=1$. On the other hand, $0=(\mu ,\alpha _j+\alpha _k)=(\theta ,\gamma _1+\gamma _2)$ and therefore $(\theta , \gamma _2)<0$, which is impossible. Thus, $w_\mu ^{-1}(\alpha _j+\alpha _k)$ must be simple. $\square$

Remark 4.13

If $(\eta ,\eta ')$ is the unique semi-glorious pair, then $\eta \vee \eta '=\eta ={\lceil \theta /2\rceil }$; whereas for all genuine glorious pairs, one has $\eta \vee \eta ' \succ {\lceil \theta /2\rceil }$. Again, if a glorious pair $(\eta ,\eta ')$ corresponds to the edge $\mathcal {E}$ and $d(\mathcal {E})$ is the distance from $\mathcal {E}$ to the edge of the semi-glorious pair, then $\eta \vee \eta '={\lceil \theta /2\rceil }+\sum _{i=1}^d \gamma _i$ and ${\mathsf {ht}}(\eta \vee \eta ')={\mathsf {ht}}({\lceil \theta /2\rceil })+d(\mathcal {E})$, cf. Remark 4.6.

6 The minimal non-abelian ideals of ${{\mathfrak {b}}}$

As an application of previous theory, we characterize the minimal non-abelian ideals in $\mathfrak {Ad}$ and point out the associated canonical elements in ${\widehat{W}}$ (cf. Sect. 1.5). By Lemma , if $\mathcal {J}\in \mathfrak {Ad}\setminus \mathfrak {Ab}$ and $\#\mathcal {J}=h^*$, then $\mathcal {J}$ is minimal non-abelian. The precise assertion is:

Theorem 5.1

An ideal $\mathcal {J}\in \mathfrak {Ad}$ is minimal non-abelian if and only if either $\min (\mathcal {J})$ is a glorious pair or $\Delta$ is non-simply laced and $\mathcal {J}=I\langle {\succcurlyeq }{\lfloor \theta /2\rfloor }\rangle$. For all these cases, $\mathcal {J}\subset {\mathcal {H}}$, $\#\mathcal {J}=h^*$, and the unique summable (to $\theta$) pair of roots in $\mathcal {J}$ is either a glorious or semi-glorious pair.

Proof

If $\mathcal {J}$ is non-abelian, then there are $\eta ,\eta '\in \mathcal {J}$ such that $\eta +\eta '=\theta$. Hence $I\langle {\succcurlyeq }\eta ,\eta '\rangle \subset \mathcal {J}$, and there must be equality if $\mathcal {J}$ is minimal. There are two possibilities now.

(a):

If $\eta ,\eta '$ are incomparable, then $\{\eta ,\eta '\}$ is a glorious pair and also $\#\mathcal {J}=h^*$, see Proposition 3.2(i). Here $\mathcal {J}=I(\alpha )_{\textsf {min}}\cup \{\eta '\}=I(\alpha ')_{\textsf {min}}\cup \{\eta \}$.

(b):

Suppose that $\eta '\preccurlyeq \eta$. Then $\mathcal {J}=I\langle {\succcurlyeq }\eta '\rangle$ and also $\eta '\in \Delta ^+_{\textsf {nc}}$. (This already excludes the ${{\mathbf {\mathsf{{{A}}}}}}_{n}$-case, where all 1-generated ideals are abelian.) Then $\eta '\preccurlyeq {\lfloor \theta /2\rfloor }$ and the minimality of $\mathcal {J}$ implies that $\eta '= {\lfloor \theta /2\rfloor }$. However, in the ${{\mathbf {\mathsf{{{DE}}}}}}_{}$-case the non-abelian ideal $I\langle {\succcurlyeq }{\lfloor \theta /2\rfloor }\rangle$ is not minimal, since it properly contains three smaller non-abelian ideals generated by the glorious pairs related to the central edges of the Dynkin diagram, see Corollary 4.4 and Fig. 2. In the ${{\mathbf {\mathsf{{{BCFG}}}}}}_{}$-case, we do obtain a minimal non-abelian ideal of cardinality $h^*$, as follows from Theorem 4.9(i). For, then $I\langle {\succcurlyeq }\eta '\rangle \setminus \{\eta '\}=I(\alpha )_{\textsf {min}}$ and $\#I(\alpha )_{\textsf {min}}=h^*-1$. $\square$

A nice uniform formulation is that the minimal non-abelian ideals are in a one-to-one correspondence with the edges of the Dynkin diagram that are incident to the long simple roots.

Remark 5.2

For a minimal non-abelian ideal $\mathcal {J}$, the canonical element ${\hat{w}}_{\mathcal {J}}\in {\widehat{W}}$ (see 1.5) can explicitly be described. Note that in both cases below, $\ell ({\hat{w}}_{\mathcal {J}})=\#\mathcal {J}+\#(\mathcal {J}^2)=h^*+1$.

(a):

Suppose that $\mathcal {J}=I\langle {\succcurlyeq }\eta ,\eta '\rangle$, where $(\eta ,\eta ')$ is the glorious pair corresponding to adjacent $\alpha ,\alpha '\in \Pi _l$. Then

$$\begin{aligned} {\hat{w}}_{\mathcal {J}}=s_{\alpha '} s_\alpha w_{\alpha }s_0=s_\alpha s_{\alpha '} w_{\alpha '}s_0. \end{aligned}$$

For, $w_{\alpha }s_0$ is the minuscule element for $I(\alpha )_{\textsf {min}}$ (Sect. 1.4). Hence ${\mathcal {N}}(w_{\alpha }s_0)=\{\delta -\gamma \mid \gamma \in I(\alpha )_{\textsf {min}}\}$. Then ${\mathcal {N}}(s_\alpha w_{\alpha }s_0)={\mathcal {N}}(w_{\alpha }s_0)\cup \{ (w_{\alpha }s_0)^{-1}(\alpha )\} ={\mathcal {N}}(w_{\alpha }s_0)\cup \{2\delta -\theta \}$, and

$$\begin{aligned} {\mathcal {N}}(s_{\alpha '}s_\alpha w_{\alpha }s_0)={\mathcal {N}}(s_\alpha w_{\alpha }s_0)\cup \{\delta -\eta '\}= \{\delta -\gamma \mid \gamma \in \mathcal {J}\}\cup \{2\delta -\theta \} . \end{aligned}$$

For the second equality, use the relations $s_\alpha w_{\alpha +\alpha '}=w_{\alpha '}$, $s_{\alpha '} w_{\alpha +\alpha '}=w_\alpha$, and $(s_\alpha s_{\alpha '})^3=1$.

(b):

If $\mathcal {J}=I\langle {\succcurlyeq }{\lfloor \theta /2\rfloor }\rangle$, then $\mathcal {J}$ can be thought of as the ideal related to the semi-glorious pair $({\lceil \theta /2\rceil },{\lfloor \theta /2\rfloor })$. If $\alpha \in \Pi _l$ and $\alpha '\in \Pi _s$ are the related adjacent roots, then similarly

$$\begin{aligned} {\hat{w}}_{\mathcal {J}}=s_{\alpha '} s_\alpha w_{\alpha }s_0 . \end{aligned}$$

Note that here $w_{\alpha '}$ does not exist and $(s_\alpha s_{\alpha '})^3\ne 1$.

Appendix A. Data for the exceptional Lie algebras

A.1 For ${{\mathbf {\mathsf{{{E}}}}}}_{6}$, ${{\mathbf {\mathsf{{{E}}}}}}_{7}$, and ${{\mathbf {\mathsf{{{E}}}}}}_{8}$, the numbering of the simple roots is

For ${{\mathbf {\mathsf{{{E}}}}}}_{6}$, ${{\mathbf {\mathsf{{{E}}}}}}_{7}$, and ${{\mathbf {\mathsf{{{E}}}}}}_{8}$, the numbering of the simple roots is

respectively.

The glorious pairs $(\eta ,\eta ')$ associated with adjacent simple roots $(\alpha ,\alpha ')$ are given below. Recall that here $\eta \in \min (I(\alpha )_{\textsf {min}})$ and ${\mathsf {cl}}(\eta )=\alpha '$.

A.2 For ${{\mathbf {\mathsf{{{D}}}}}}_{n}$ and ${{\mathbf {\mathsf{{{E}}}}}}_{n}$, the explicit correspondence between tails and odd roots is presented below. The numbering of tails follows Fig. 1. That is, according to the chosen numbering of $\Pi$, see Example 3.8 and figures in Sect. 1, ${{\mathcal {T}}}_1$ contains $\alpha _1$, ${{\mathcal {T}}}_2$ contains $\alpha _{n-1}$, and ${{\mathcal {T}}}_3$ contains $\alpha _n$. In particular, we always have $\#{{\mathcal {T}}}_3=1$. Then the odd root $\beta _i$ corresponding to ${{\mathcal {T}}}_i$ is:

A.3 Here we provide the transition roots for the pairs of incident edges in types ${{\mathbf {\mathsf{{{E}}}}}}_{6}$, ${{\mathbf {\mathsf{{{E}}}}}}_{7}$, and ${{\mathbf {\mathsf{{{E}}}}}}_{8}$, and thereby explicitly present the bijection of Remark 3.13.