Abstract
There is a famous criterion for objective wave function reduction which is derived by using the Shrödinger–Newton equation [L Diosi, Phys. Lett. A 105(4–5), 199 (1984)]. In this regard, a critical mass for the transition from quantum world to the classical world is determined for a particle or an object. In this paper, we shall derive that criterion by using the concept of Bohmian trajectories. This study has two consequences. The first is, it provides a geometric framework for the problem of wave function reduction. The second is, it represents the role of quantum and gravitational forces in the reduction process.




Similar content being viewed by others
References
L Diosi, Phys. Lett. A 105(4–5), 199 (1984)
F Karolyhazy, Nuovo Cimento A 42, 390 (1966)
L Diosi, Phys. Lett. A 120(8), 377 (1987)
L Diosi, Phys. Rev. A 40, 1165 (1989)
A Bassi, K Lochan, S Satin, T P Singh and H Ulbricht, Rev. Mod. Phys. 85, 471 (2013)
R Penrose, Gen. Relativ. Gravit. 28(5), 581 (1996)
R Penrose, J. Phys.: Conf. Ser. 174012001 (2009)
R Penrose, Found. Phys. 44, 557 (2014)
P R Holland, The quantum theory of motion (Cambridge University Press, Cambridge, 1993)
J J Sakurai and J Napolitano, Modern quantum mechanics (Cambridge University Press, 2017)
K Landsman, The measurement problem, in: Foundations of quantum theory. Fundamental theories of physics (Springer, Cham, 2017) Vol. 188
J Von Neumann, Mathematical foundations of quantum mechanics (Princeton University Press, 1996)
J A Wheeler and W H Zurek, Quantum theory and measurement (Princeton University Press, 1983)
F J Belinfante, A survey of hidden-variables theories (Elsevier Science and Technology, 1973)
G C Ghirardi, A Rimini and T Weber, Quantum probability and applications II (1984) pp. 223–232
G C Ghirardi, A Rimini and T Weber, Phys. Rev. D 34, 470 (1986)
V Allori, S Goldstein, R Tumulka and N Zanghi, On the common structure of Bohmian mechanics and the Ghirardi–Rimini–Weber theory, arXiv:quant-ph/0603027
N Gisin, Phys. Lett. A 143(1–2) 1 (1990)
R W Carrol, Fluctuations, information, gravity and the quantum potential (Springer, Netherlands, 2006)
F Shojai and M Golshani, Int. J. Mod. Phys. A 13(4), 677 (1998)
I Licata and D Fiscaletti, Quantum potential: Physics, geometry and algebra (Springer International Publishing, 2014)
F Rahmani, M Golshani and M Sarbishei, Pramana – J. Phys. 86(4), 747 (2016)
Bryce Seligman Dewitt and Neill Graham, The many worlds interpretation of quantum mechanics (Princeton Series in Physics, 2015)
Max Tegmark, Fortsch. Phys. 46, 855 (1998)
H Everett, Rev. Mod. Phys. 29, 454 (1957)
J A Wheeler, Rev. Mod. Phys. 29, 463 (1973)
David Wallace, The emergent multiverse: Quantum theory according to the Everett interpretation (Oxford University Press, 2014), ISBN 978-0-19-954696-1
D Bohm, Phys. Rev. 85(2), 166 (1952)
D Bohm, Wholeness and the implicate order (Routledge & Kegan Paul, 1980)
D Bohm and B J Hiley, The undivided universe: An ontological interpretation of quantum theory (Routledge, 1993)
The Bohmian quantum potential for the relativistic electron has been derived recently by Hiley and co-workers through complicated methods of Clifford algebra \(C^{0}_{3}\,[33]\). There, the quantum potential is considered as additional term in the Hamilton–Jacobi equation of the electron and is obtained by comparing with the original equation \(p_\mu p^\mu =m^2\). In other words, in that case too the relation \(p_\mu p^\mu ={\cal{M}}^2\) holds, where \(\cal{M}^2=m^2+Q_{\text{Dirac}}\)
The polar form substitution of the wave function into the Klein–Gordon equation is not the only way to get the Hamilton–Jacobi equation (11)
B J Hiley and R E Callaghan, Found. Phys. 42, 192 (2012)
F Rahmani and M Golshani, Int. J. Theor. Phys. 56, 3096 (2017)
F Rahmani, M Golshani and Gh Jafari, Int. J. Mod. Phys. A 33(22) (2018), https://doi.org/10.1142/S0217751X18501294
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rahmani, F., Golshani, M. & Jafari, G. A geometric look at the objective gravitational wave function reduction. Pramana - J Phys 94, 163 (2020). https://doi.org/10.1007/s12043-020-02032-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12043-020-02032-6
Keywords
- Gravitational reduction of the wave function
- Bohmian quantum potential
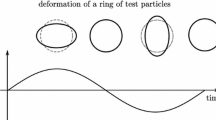
- Bohmian geodesic deviation equation
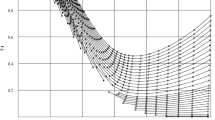
- Bohmian trajectories