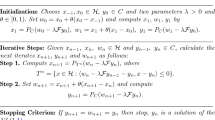Skip to main content

Advertisement

SpringerLink
Log in

A general inertial projected gradient method for variational inequality problems

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

The purpose of this article is to introduce a general inertial projected gradient method with a self-adaptive stepsize for solving variational inequality problems. The proposed method incorporates two different extrapolations with respect to the previous iterates into the projected gradient method. The weak convergence for our method is proved under standard assumptions without any requirement of the knowledge of the Lipschitz constant of the mapping. Furthermore, R-linear convergence rate is established under the strong monotonicity assumption of the mapping. Finally preliminary results from numerical experiments and applications to optimal control problems are performed which show the advantage of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Alt W, Baier R, Gerdts M, Lempio F (2012) Error bounds for Euler approximation of linear-quadratic control problems with bang-bang solutions. Numer Algebra Control Optim 2:547–570

    Article  MathSciNet  Google Scholar 

  • Antipin AS (1976) On a method for convex programs using a symmetrical modification of the Lagrange function. Ekonomika i Matematicheskie Metody 12(6):1164–1173

    Google Scholar 

  • Bauschke HH, Combettes PL (2017) Convex analysis and monotone operator theory in Hilbert spaces, 2nd edn. Springer, Berlin

  • Beck A, Teboulle M (2009) A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci 2(1):183–202

    Article  MathSciNet  Google Scholar 

  • Bressan B, Piccoli B (2007) Introduction to the mathematical theory of control, In: Volume 2 of AIMS Series on Applied Mathematics. American Institute of Mathematical Sciences (AIMS), Springfield, MO

  • Censor Y, Gibali A, Reich S (2011) The subgradient extragradient method for solving variational inequalities in Hilbert space. J Optim Theory Appl 148:318–335

    Article  MathSciNet  Google Scholar 

  • Dong Y (2021) New inertial factors of the Krasnosel’skiǐ–Mann iteration. Set-Valued Var Anal 29:145–161

  • Dong QL, Lu YY, Yang J (2016) The extragradient algorithm with inertial effects for solving the variational inequality. Optimization 65:2217–2226

    Article  MathSciNet  Google Scholar 

  • Dong QL, Cho YJ, Rassias TM (2018a) General inertial Mann algorithms and their convergence analysis for nonexpansive mappings. In: Rassias TM (ed) Applications of nonlinear analysis. Springer, pp 175–191

  • Dong QL, Cho YJ, Zhong LL et al (2018b) Inertial projection and contraction algorithms for variational inequalities. J Glob Optim 70(3):687–704

  • Dong QL, Yuan HB, Cho YJ et al (2018c) Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim Lett 12:87–102

  • Dong QL, Huang J, Li XH et al (2019a) MiKM: multi-step inertial Krasnosel’skiǐ-Mann algorithm and its applications. J Glob Optim 73(4):801–824

  • Dong QL, Yang J, Yuan HB (2019b) The projection and contraction algorithm for solving variational inequality problems in Hilbert spaces. J Nonlinear Convex Anal 20:111–122

  • Dong QL, He S, Cho YJ, Rassias TM (2021) The Krasnosel’skiǐ–Mann iterative method—recent progress and applications, preprint

  • Facchinei F, Pang JS (2003) Finite-dimensional variational inequality and complementarity problems. Springer, New York

    MATH  Google Scholar 

  • Fichera G (1963) Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad Naz Lincei VIII Ser Rend Cl Sci Fis Mat Nat 34:138–142

  • Giselsson P, Fält M, Boyd S (2016) Line search for averaged operator iteration. In: 2016 IEEE 55th conference on decision and control (CDC). IEEE, pp 1015–1022

  • Harker PT, Pang JS (1990) A damped-Newton method for the linear complementarity problem. In: Allgower G, Georg K (eds). Computational solution of nonlinear systems of equations. Providence, RI: AMS. pp 265–284 (Lectures in Applied Mathematics; 26)

  • He BS (1997) A class of projection and contraction methods for monotone variational inequalities. Appl Math Optim 35:69–76

    Article  MathSciNet  Google Scholar 

  • He S, Dong QL, Tian H (2020) On the optimal parameters of Krasnosel’skii–Mann iteration. Optimization. https://doi.org/10.1080/02331934.2020.1753741

  • Hieu DV, Anh PK, Muu LD (2017) Modified hybrid projection methods for finding common solutions to variational inequality problems. Comput Optim Appl 66:75–96

    Article  MathSciNet  Google Scholar 

  • Hieu DV, Strodiot JJ, Muu LD (2020) An explicit extragradient algorithm for solving variational inequalities. J Optim Theory Appl 185:476–503

    Article  MathSciNet  Google Scholar 

  • Korpelevich GM (1976) The extragradient method for finding saddle points and other problems. Ekon Mat Metody 12:747–756

    MathSciNet  MATH  Google Scholar 

  • La Cruz W (2018) A residual algorithm for finding a fixed point of a nonexpansive mapping. J Fixed Point Theory Appl 20(3):116

    Article  MathSciNet  Google Scholar 

  • Mainge PE (2008) Convergence theorems for inertial \(KM\)-type algorithms. J Comput Appl Math 219:223–236

    Article  MathSciNet  Google Scholar 

  • Mainge PE, Gobinddass ML (2016) Convergence of one-step projected gradient methods for variational inequalities. J Optim Theory Appl 171:146–168

    Article  MathSciNet  Google Scholar 

  • Malitsky Y (2015) Projected reflected gradient methods for variational inequalities. SIAM J Optim 25(1):502–520

    Article  MathSciNet  Google Scholar 

  • Malitsky Y (2020) Golden ratio algorithms for variational inequalities. Math Prog 184:383–410

    Article  MathSciNet  Google Scholar 

  • Malitsky Y, Tam MK (2020) A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J Optim 30(2):1451–1472

    Article  MathSciNet  Google Scholar 

  • Polyak BT (1964) Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys 4:1–17

  • Popov LD (1980) A modification of the Arrow-Hurwicz method for searching for saddle points. Mat Zametki 28:777–784

    MathSciNet  MATH  Google Scholar 

  • Preininger J, Vuong PT (2018) On the convergence of the gradient projection method for convex optimal control problems with bang-bang solutions. Comput Optim Appl 70:221–238

    Article  MathSciNet  Google Scholar 

  • Shehu Y, Iyiola OS (2020) Projection methods with alternating inertial steps for variational inequalities: weak and linear convergence. Appl Numer Math 157:315–337

    Article  MathSciNet  Google Scholar 

  • Stampacchia G (1964) Forms bilineaires coercitives sur les ensembles convexes. C R Acad Sci Paris 258:4413–4416

    MathSciNet  MATH  Google Scholar 

  • Sun D (1994) A projection and contraction method for the nonlinear complementarity problems and its extensions. Math Numer Sin 16:183–194

    Article  MathSciNet  Google Scholar 

  • Thong DV, Hieu DV (2018) Modified Tseng’s extragradient algorithms for variational inequality problems. J Fixed Point Theory Appl 20:152

    Article  MathSciNet  Google Scholar 

  • Thong DV, Li X, Dong Q (2021) An inertial Popov’s method for solving pseudomonotone variational inequalities. Optim Lett 15:757–777

  • Tseng P (2000) A modified forward-backward splitting method for maximal monotone mapping. SIAM J Control Optim 38:431–446

    Article  MathSciNet  Google Scholar 

  • Vuong PT, Shehu Y (2019) Convergence of an extragradient-type method for variational inequality with applications to optimal control problems. Numer Algor 81(1):269–291

    Article  MathSciNet  Google Scholar 

  • Wen B, Chen X, Pong TK (2018) A proximal difference-of-convex algorithm with extrapolation. Comput Optim Appl 69:297–324

    Article  MathSciNet  Google Scholar 

  • Wu Z, Li M (2019) General inertial proximal gradient method for a class of nonconvex nonsmooth optimization problems. Comput Optim Appl 73:129–158

    Article  MathSciNet  Google Scholar 

  • Yang J, Liu H (2018) A modified projected gradient method for monotone variational inequalities. J Optim Theory Appl 179:197–211

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We sincerely thank the anonymous reviewers for their constructive comments and suggestions that greatly improved the manuscript. This work was supported by Fundamental Research Funds for the Central Universities (No. 3122019142)

Author information

Authors and Affiliations

  1. Tianjin Key Laboratory for Advanced Signal Processing and College of Science, Civil Aviation University of China, Tianjin, 300300, China

    Qiao-Li Dong, Songnian He & Lulu Liu

Authors
  1. Qiao-Li Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Songnian He
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lulu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiao-Li Dong.

Additional information

Communicated by Ernesto G. Birgin.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dong, QL., He, S. & Liu, L. A general inertial projected gradient method for variational inequality problems. Comp. Appl. Math. 40, 168 (2021). https://doi.org/10.1007/s40314-021-01540-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-021-01540-4

Keywords

Mathematics Subject Classification

Search

Navigation