Abstract
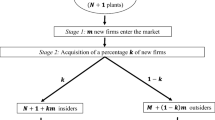
My objective is to better understand how a business should expand through acquisition. In a differentiated market where firms first choose quality and then compete in prices, the idea is to analyze acquisition as an expansion strategy. The specific questions I consider are the following: (a) is it better to acquire a direct or an indirect competitor? (b) how are the quality levels affected by acquisition and does it matter whether the path to increase quality is fixed costs or costs that depend on the volume of sales? (c) how are profits affected by acquisition? (d) how are prices affected by acquisition? and (e) what are the welfare effects of acquisition? To study these questions, I employ a spatial model in which each attractive location in the market is occupied by a business. The analysis shows that a firm enjoys superior profitability by acquiring a direct competitor. This obtains because independent of quality, the ability to coordinate prices with the acquisition of a direct competitor is strong: this reduces the intensity of price competition. Second, the model shows that the synergy created by direct mergers is inversely related to the cost of building quality when higher quality comes from fixed investments and is unaffected by the cost of quality when the costs depend on the volume of sales. Third, the model shows that post-acquisition, the merged firm implements reductions in quality when higher quality comes from fixed investments but chooses the same quality when higher quality is delivered by higher variable costs. Competitors respond by increasing quality in the first case and by leaving quality unchanged in the second case. In addition, when higher quality comes from fixed investment, direct acquisitions create a market outcome where price and quality are negatively correlated. Finally, the model shows that the effect of acquisition on total welfare is ambiguous in the case of fixed investment; however, it is unambiguously lower when higher quality comes from higher variable costs.





Similar content being viewed by others
Change history
04 November 2022
In Table 1, the second last entry was changed from "Burger King acquires Tim Horton'" to "Burger King acquires Tim Hortons".
Notes
Often, competition in markets is such that the acquisition of one firm by another has relatively small effects on total welfare.
The model applies to markets where the level of quality can be adjusted more easily than the horizontal location. For example, it is easier for a Quick Service Restaurant to modify the service experience of customers than to change its cuisine category (to move from burgers to pizza for example).
The economies may be in terms of manufacturing, distribution, servicing and/or administration.
Similarly, Giraud-Heraud et al. [15] find that acquisitions of adjacent competitors are more profitable in horizontal markets restricted to price competition.
The literature recognizes that mergers may have an impact on product quality. Willig [41] discusses the impact on total welfare of changes in quality due to a merger when the change in quality is exogenous.
The model of Shaked and Sutton consists of three stages where the first stage is an entry decision. the second stage is a choice of quality and the third stage is a choice of prices.
The findings are affected by the sequential nature of the quality and price decisions. Contexts where quality and price are chosen simultaneously are less common.
Similar to Levy and Reitzes [20], the “merged” firm continues to operate from two locations.
There are contexts where a firm might merge due to its profits being reduced if two competitors merge; however, that is not a factor in this framework. Even firms “on the outside” benefit from the reduced intensity of competition.
When the equilibrium is determined, the outcomes are checked to ensure that the assumption is justified.
In equilibrium (with t normalized to 1 and the marginal cost normalized to zero), \(v\geqq \frac {3}{8}\) is sufficient to ensure coverage.
Lemma 3 is conditional on β being greater than a threshold that is sufficient for the existence of a unique equilibrium. Details about the limit for β such the conditions for uniqueness are satisfied are provided in the A.
In competitive models, when the best responses of competitors for a key decision (like price or quantity) are positively correlated, they are known as strategic complements. When they are negative correlated, they are known as strategic substitutes [5].
As noted in the previous section, the quality of offers is unaffected by acquisition when costs that are proportional to the quantity sold are used to increase quality.
In [4], acquisition leads to an average quality increase. However, in a 3 firm model, there are only two firms after an acquisition. As a result, the incentives of the sole outside firm to increase quality are amplified.
The European Commission decision was rendered on June 27, 2007 (Case # COMP/M.4439).
The details of the acquisition are provided in https://globalnews.ca/news/1724238/its-official-tim-hortons-burger-king-become-one/
Background on the challenge of improving quality in QSRs is available at https://www.paystone.com/blog/7-tips-to-improve-the-customer-experience-in-your-restaurantput, https://benbria.com/4-elements-of-cx-that-every-qsr-should-measure/ and, https://www.usa-shade.com/resources/articles/ways-to-enhance-your-qsr-experience.
Background is available at https://www.scrapehero.com/top-fast-food-chains-in-canada/. Because Burger King is a strictly controlled global brand and its Canadian operations are relatively small, the flexibility of RBI to adjust the quality of Burger King in Canada is limited.
Background on Burger King is available at https://www.eatthis.com/news-burger-king-decline/ and https://www.forbes.com/sites/jonhartley/2014/08/25/burger-kings-tax-inversion-and-canadas-favorable-corporate-tax-rates/?sh=5c4edb6c3ed7.
These results are discussed in https://www.cbc.ca/news/business/rbi-tim-hortons-popeyes-burger-king-earnings-1.5458089
Brekke et al. [4] find that total welfare can increase when demand is sufficiently responsive to quality. This finding is related to my explanation; invariably, total welfare can increase when acquisition leads to more efficient investments in quality.
The economies may be in terms of manufacturing, distribution, servicing and/or administration.
Often the focus of acquisition strategy is economies and complementarities unlocked through acquisition.
References
Armstrong M, Chen Y (2009) Inattentive consumers and product quality. J Eur Econ Assoc 7(2–3):411–422
Atmar H, Hudson S, Koshy A, Rickert S, Slelatt R (2020) The next normal in consumer: Implications for Consumer Goods M&A. McKinsey Consumer Packaged Goods, June 24. https://www.mckinsey.com/industries/consumer-packaged-goods/our-insights/the-next-normal-in-consumer-implications-for-consumer-goods-m-and-a. Accessed 21 Oct 2022
Brander J, Eaton J (1984) Product line rivalry. Am Econ Rev 74:323–334
Brekke KR, Siciliani L, Straume OR (2017) Horizontal mergers and product quality. Canadian J Econ 50(4):1063–1103
Bulow J, Geanakoplos J, Klemperer P (1985) Multimarket oligopoly: strategic substitutes and strategic complements. J Polit Econ 93:488–511
Chambers C, Kouvelis P, Semple J (2006) Quality-Based Competition, profitability, and variable costs. Manag Sci 52(12):1884–1895
Chioveanu I (2012) Price and quality competition. J Econ 107(1):p23-44
Davidson C, Deneckere R (1984) Horizontal mergers and collusive behavior. Int J Ind Organ 2(2):117–132
Davidson C, Deneckere R (1985) Incentives to form coalitions with Bertrand competition. Rand J Econ 16(4):473–486
Esteban L, Hernández J (2014) Endogenous direct advertising and price competition. J Econ 112(3):p225-251
Fan Y (2013) Ownership consolidation and product characteristics: a study of the US daily newspaper market. Am Econ Rev 103(5):1598–1628
Farrell J, Shapiro C (1990) Horizontal mergers: an equilibrium analysis. Am Econ Rev 80(1):107–126
Ghose A, Huang Ke-Wei (2009) Personalized pricing and quality customization. J Econ Manag Strategy 18(4):p1095-1135
Ghosh B, Balachander S (2007) Competitive bundling and counterbundling with generalist and specialist firms. Manag Sci 53(1):159–168
Giraud-Heraud E, Hammoudi H, Mokrane M (1999) Industrial structure and strategic takeover in a differentiated market working paper 99-34, Paris X - Nanterre, U.F.R. de Sc. Ec. Gest. Maths Infor
Giraud-Heraud E, Hammoudi H, Mokrane M (2003) Multiproduct firm behavior in a differentiated market. Can J Econ 36(1):41–61
Hotelling H (1929) Stability in competition. Econ J 39:41–57
Iyer G (1998) Coordinating channels under price and nonprice competition. Mark Sci 17(4):338–355
Kirby J (2020) Maple glazed Tim Hortons. Macleans 133(3):36–37
Levy DT, Reitzes JD (1992) Anticompetitive effects of mergers in markets with localized competition, Journal of Law. Econ Organ 8(2):427–440
Lilien GL, Kotler P, Moorthy S (1992) Marketing models. Prentice-Hall, Inc, Englewood Cliffs, New Jersey, pp 223–236
Maskin E, Riley J (1984) Monopoly with incomplete information. Rand J Econ 15(2):171–196
McAfee R, Simons J, Williams M (1992) Preston horizontal mergers in spatially differentiated noncooperative markets. J Ind Econ 40(4):349–358
Mendelson H, Parlaktürk AK (2008) Product-line competition: Customization vs Proliferation. Manage Sci 54(12):2039–2053
Moorthy KS (1988) Product and price competition in a duopoly. Mark Sci 7(2):141–168
Motta M (1993) Endogenous quality Choice:Price versus quantity competition. J Ind Econ 41(2):113–131
Mussa M, Rosen S (1978) Monopoly and product quality. J Econ Theory 18(2):301–317
Norman G, Pepall L (2000) Profitable mergers in a cournot model of spatial competition. South Econ J 66(3):667–681
Panzar JC, Willig RD (1981) Economies of scope. Am Econ Rev 71(2):268–272
Perry MK, Porter RH (1985) Oligopoly and the incentive for horizontal merger. Am Econ Rev 75(1):219–227
Rhee B-D (1996) Consumer heterogeneity and strategic quality decisions. Manag Sci 42(2):157–172
Rothschild R (2000) Mergers under spatial competition, urban studies, special issue: location theory. Anal Appl 37(3):443–449
Salop S (1979) Monopolistic competition with outside goods. Bell J Econ 10(1):141–156
Shaked A, Sutton J (1982) Relaxing price competition through product differentiation. Rev Econ Stud 49(155):3–13
Stigler GJ (1950) Monopoly and oligopoly by merger. Am Econ Rev (Papers and Proceedings) 40:23–34
Tenn S, Froeb L, Tschantz S (2010) Mergers when firms compete by choosing both price and promotion. Int J Ind Organ 28(6):695–707
Tirole J (1988) The theory of industrial organization. MITPress, Cambridge Massacchusetts
Wernerfelt B (1986) Product line rivalry. Am Econ Rev 76(4):842–844
Wolinsky A (1983) Prices as signals of product quality. Rev Econ Stud 50(4):647–658
Williamson O (1968) Economies as an Antitrust defense: The welfare tradeoffs. Am Econ Rev 58(1):18–36
Willig R (2011) Unilateral competitive effects of mergers: upward pricing pressure, product quality, and other extensions. Rev Ind Organ 39(1/2):19–38
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The author declares no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
Proof of Lemma 1
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
The unique solution to this game is \(q_{A}=q_{B}=q_{C}=q_{D}=\frac {5}{ 48\beta }\). This implies equilibrium prices of \(\frac {1}{4}\) and profits of \(\frac {144\beta -25}{2304\beta }\) for all firms. To ensure that the equilibrium is a unique maximum for all 4 players, two conditions must be satisfied. First, the matrix of first order conditions must be of full rank. The second condition is that the second order conditions be satisfied for all 4 firms.
The matrix of first order conditions A is
The determinant of A is \(\frac {1}{648}\beta \left (18\beta -5\right ) \left (24\beta -5\right )^{2}\). In order for A to be non-singular, \(\beta \notin \left \{ 0,\frac {5}{24},\frac {5}{18}\right \}\) is required and the second order conditions are satisfied when \(\frac {25}{72}-2\beta <0\Rightarrow \beta >\frac {25}{144}\). Hence, we restrict our attention to the parameter space \(\beta >\frac {25}{144}\) where the matrix A is non-singular and the second order conditions are satisfied.
Proof of Lemma 2
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
The symmetric solution to this problem is \(q_{A}=q_{B}=q_{C}=q_{D}=\frac {1}{ 2\beta }\). The second order conditions at this fixed point are \(\frac { \partial ^{2}\pi _{A}}{\partial {q_{A}^{2}}}=\frac {\partial ^{2}\pi _{B}}{ \partial {q_{B}^{2}}}=\frac {\partial ^{2}\pi _{C}}{\partial {q_{C}^{2}}}=\frac { \partial ^{2}\pi _{D}}{\partial {q_{D}^{2}}}=-\frac {5}{12}\beta <0\) implying that all firms are maximizing their choice of quality. This solution implies that \(p_{A}=p_{B}=p_{C}=p_{D}=\frac {1}{4\beta }\left (\beta +1\right )\) and \(\pi _{A}=\pi _{B}=\pi _{C}=\pi _{D}=\frac {1}{16}\).
Proof of Lemma 3
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
The unique solution to this game is \(q_{A}=q_{B}=\frac {57-290\beta }{ 575\beta -3625\beta ^{2}}\) and \(q_{C}=q_{D}=\frac {114-855\beta }{1150\beta -7250\beta ^{2}}\). This implies \(p_{A}=p_{B}=\frac {1}{5}\frac {290\beta -57}{ 145\beta -23}\) and profit for the merged firm of \(\frac {\left (25\beta -2\right ) \left (290\beta -57\right ) ^{2}}{625\beta \left (145\beta -23\right )^{2}}\). The competitors prices are \(\frac {29}{10}\frac {15\beta -2 }{145\beta -23}\) and the profit of each competitor is \(\frac {\left (21 025\beta -3249\right ) \left (15\beta -2\right )^{2}}{2500\beta \left (145\beta -23\right )^{2}}\). To ensure that the equilibrium is a unique maximum for all players, three conditions must be satisfied. First, the matrix of first order conditions must be of full rank. Second, the Hessian matrix for the two product firm must negative semi-definite. Third, the second order conditions must be satisfied for all 3 firms.
The matrix of first order conditions A is
The determinant of A is\(\frac {16\beta \left (145\beta -23\right ) \left (-70 731\beta +121 945\beta ^{2}+9576\right ) }{17 682 025}\). There are three values of β that would lead to the determinant of A being zero. In order for the determinant of A to be non-zero, \(\beta \notin \left \{ 0,\frac {23}{145},\frac {2439-3\sqrt {43 849}}{8410},\frac {3\sqrt { 43 849}+2439}{8410}\right \}\) is required.
The Hessian matrix for the merged firm must be negative semi-definite. The Hessian matrix is:
The derivative of the principal minors and the relevant conditions are as follows:
Principal minor | Determinant | Condition | Condition on β | Numeric |
|---|---|---|---|---|
1st | \(\frac {9032}{21 025}-2\beta\) | negative | \(\beta >\frac {4516}{21 025}\) | 0.21479 |
2nd | \(4\beta ^{2}-\frac {36 128}{21 025}\beta +\frac {2352}{21 025 }\) | positive | \(\beta > \frac {294}{841}\) | 0.34958 |
The second order condition for the merged firm is the 1st principal minor of the Hessian. For the independent competitors, the second order conditions are satisfied when \(\frac {\partial ^{2}\pi _{C}}{\partial {q_{C}^{2}}}=\frac {\partial ^{2}\pi _{D}}{\partial {q_{D}^{2}}}=\frac {6498}{ 21 025}-2\beta \Rightarrow \beta >\frac {3249}{21 025}\thickapprox 0.154 53\). Hence, we restrict our attention to the parameter space \(\beta > \frac {3\sqrt {43 849}+2439}{8410}\thickapprox 0.364 71\) where the matrix A is non-singular, the Hessian matrix of the two product firm is negative semi-definite and the second order conditions are satisfied.
Proof of Lemma 4
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
The unique solution to this game is \(q_{A}=q_{C}=\frac {5-18\beta }{54\beta -216\beta ^{2}}\) and \(q_{B}=q_{D}=\frac {10-45\beta }{108\beta -432\beta ^{2}}\). This implies pA = pC = \(\frac {1}{18}\frac {18\beta -5}{4\beta -1}\) and profit for the merged firm of \(\frac {\left (9\beta -1\right ) \left (18\beta -5\right )^{2}}{1458\beta \left (4\beta -1\right )^{2}}\). The competitors prices are \(\frac {1}{9}\frac {9\beta -2}{4\beta -1}\) and the profit of each competitor is \(\frac {\left (9\beta -2\right )^{2}\left (144\beta -25\right ) }{11 664\beta \left (4\beta -1\right )^{2}}\). To ensure that the equilibrium is a unique maximum for all players, three conditions must be satisfied. First, the matrix of first order conditions must be of full rank. Second, the Hessian matrix for the merged firm must negative semi-definite. Third, the second order conditions must be satisfied for all 3 firms.
The matrix of first order conditions A is
The determinant of A is \(16\beta ^{4}-\frac {34}{3}\beta ^{3}+\frac {8}{3} \beta ^{2}-\frac {5}{24}\beta\). There are three values of β that would lead to the determinant of A being zero. In order for the determinant of A to be non-zero, \(\beta \notin \left \{ 0,\frac {5}{24}, \frac {1}{4}\right \}\) is required. The Hessian matrix for the merged firm must be negative semi-definite. The Hessian matrix is:
The derivative of the principal minors and the relevant conditions are as follows:
Principal minor | Determinant | Condition | Condition on β | Numeric |
|---|---|---|---|---|
1st | \(\frac {13}{36}-2\beta\) | negative | \(\beta >\frac {13}{72}\) | 0.18056 |
2nd | \(4\beta ^{2}-\frac {13}{9}\beta +\frac {1}{9}\) | positive | \(\beta >\frac {1 }{4}\) | 0.25 |
The second order condition for the merged firm is the 1st principal minor of the Hessian. For the independent firms, the second order conditions are satisfied when \(\frac {\partial ^{2}\pi _{B}}{\partial {q_{B}^{2}}}=\frac {\partial ^{2}\pi _{D}}{\partial {q_{D}^{2}}}=\frac {25}{72} -2\beta \Rightarrow \beta >\frac {25}{144}\thickapprox 0.173 61\). Hence, we restrict our attention to the parameter space \(\beta >\frac {1}{4}\) where the matrix A is non-singular, the Hessian matrix of the two product firm is negative semi-definite and the second order conditions are satisfied.
Proof of Proposition 1
Using the expressions in Lemmas 3 and 4, the difference between the profit with a direct takeover and the profit with an indirect takeover is \({\Delta }_{direct\ vs.\ indirect}=\frac {211 973 828\beta -3075 376 271\beta ^{2}+19 990 524 690\beta ^{3}-59 964 200 775\beta ^{4}+67 439 790 000\beta ^{5}-4833 836}{ 7290 000\beta \left (145\beta -23\right )^{2}\left (4\beta -1\right )^{2}}\). Because the denominator is positive, the sign of the numerator determines the sign of Δdirect vs. indirect. The numerator is a polynomial of degree 5 that is positive for all values of \(\beta \gtrapprox 0.304 86\). The allowable zone for \(\beta >\frac {3\sqrt {43 849}+2439}{8410}\thickapprox 0.364 71\) (Lemma 3), hence Δdirect vs. indirect > 0. Next, I consider the comparative static of Δdirect vs. indirect with respect to β.
In the allowable range for β, the denominator is positive so the sign of the numerator determines the sign of \(\frac {\partial {\Delta }_{direct\ vs.\ indirect}}{\partial \beta }\). The numerator is a polynomial of degree 6 that is positive for all values of \(\beta \gtrapprox 0.223 91\). The allowable zone for \(\beta >\frac {3\sqrt {43 849}+2439}{8410}\thickapprox 0.364 71\), hence \(\frac {\partial {\Delta }_{direct\ vs.\ indirect}}{\partial \beta }>0\). Using the expressions in Lemmas 1 and 3, the difference between the profit with a direct takeover and the combined pre-acquisition profit (of the two firms) is \({\Delta }_{direct\ vs.\ pre-acq}=\frac {529 830 000\beta ^{3}-217 078 775\beta ^{2}+17 912 690\beta +779 929}{720 000\beta \left (145\beta -23\right )^{2}}\). Because the denominator is positive, the sign of the numerator determines the sign of Δadj vs. indirect. The numerator is a polynomial of degree 3 that is positive for all values of \(\beta \gtrapprox 0.153 74\). The allowable zone for \(\beta >\frac {3\sqrt { 43 849}+2439}{8410}\thickapprox 0.364 71\) (Lemma 3), hence Δdirect vs. pre−acq > 0. Next, I consider the comparative static of Δdirect vs. pre−acq with respect to β. \(\frac {\partial {\Delta }_{direct\ vs.\ pre-acq}}{\partial \beta }=\frac { \left (-7104 242 375\beta ^{3}+201 868 275\beta ^{2}+339 269 115\beta -17 938 367\right ) }{-720 000\beta ^{2}\left (145\beta -23\right )^{3}}\). In the allowable range for β, the denominator is negative so the sign of the numerator determines the sign of \(\frac {\partial {\Delta }_{direct\ vs.\ pre-acq}}{\partial \beta }\). The numerator is a polynomial of degree 3 that is negative for all values of \(\beta \gtrapprox 0.152 34\). The allowable zone for \(\beta >\frac {3\sqrt {43 849}+2439}{8410}\thickapprox 0.364 71\), hence \(\frac {\partial {\Delta }_{direct\ vs.\ pre-acq}}{\partial \beta }>0\).
Proof of Lemma 5
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
There are five symmetric solutions to this problem.
-
1.
\(\left [ q_{A,B}=\frac {1}{2\beta },q_{C,D}=\frac {1}{2}\sqrt {\frac {1}{ \beta }}\left (\sqrt {\frac {1}{\beta }}+\sqrt {6}\right ) \right ]\)
-
2.
\(\left [ q_{A,B}=-\frac {1}{2\beta }\left (2\beta ^{2}\sqrt {\frac {1}{ \beta ^{3}}}-1\right ) ,q_{C,D}=\frac {1}{2\beta }\right ]\)
-
3.
\(\left [ q_{A,B}=\frac {1}{2\beta }\left (2\beta ^{2}\sqrt {\frac {1}{ \beta ^{3}}}+1\right ) ,q_{C,D}=\frac {1}{2\beta }\right ]\).
-
4.
\(\left [ q_{A,B}=\frac {1}{2\beta },q_{C,D}=\frac {1}{2\beta }\right ]\)
-
5.
\(\left [ q_{A,B}=\frac {1}{2\beta },q_{C,D}=\frac {1}{2}\left (\sqrt { \frac {1}{\beta }}-\sqrt {6}\right ) \sqrt {\frac {1}{\beta }}\right ]\)
The only solution which satisfies the second order conditions and the feasibility conditions is \(\left [ q_{A,B}=\frac {1}{2\beta },q_{C,D}= \frac {1}{2\beta }\right ]\). The other roots are infeasible. They involve the merged firm capturing the entire market or the competitors capturing the entire market (Roots 1 and 3). They are “local maxima” due to the nature of profit functions but are not best responses. Roots 2 and 5 entail choices of negative quality. The equilibrium prices are \(p_{A,B}=\frac {1}{20\beta } \left (8\beta +5\right )\) and \(p_{C,D}=\frac {1}{20\beta }\left (6\beta +5\right )\). The merged firm earns profit of \(\frac {4}{25}\) and the competitors earn \(\frac {9}{100}\). The merged firm realizes a 28% increase in profit compared to the pre-acquisition profit of the two firms. The competitors realize a 44% increase in profit due to acquisition.
Proof of Lemma 6
Using the demand functions provided in the main text, the following first order conditions for the final stage of the game must be satisfied.
These conditions imply prices of:
I substitute into each firm’s objective function to obtain first order conditions for the first stage of the game.
There are five symmetric solutions to this problem.
-
1.
\(\left [ q_{A,C}=\frac {1}{2\beta },q_{B,D}=\frac {1}{2}\sqrt {\frac {1}{ \beta }}\left (\sqrt {\frac {1}{\beta }}+\sqrt {3}\right ) \right ]\)
-
2.
\(\left [ q_{A,C}=\frac {1}{2\beta },q_{B,D}=\frac {1}{2\beta }\right ]\)
-
3.
\(\left [ q_{A,C}=\frac {1}{2\beta },q_{B,D}=\frac {1}{2}\left (\sqrt { \frac {1}{\beta }}-\sqrt {3}\right ) \sqrt {\frac {1}{\beta }}\right ]\)
-
4.
\(\left [ q_{A,C}=-\frac {1}{2\beta }\left (\sqrt {3}\beta ^{2}\sqrt {\frac { 1}{\beta ^{3}}}-1\right ) ,q_{B,D}=\frac {1}{2\beta }\right ]\)
-
5.
\(\left [ q_{A,C}=\frac {1}{2\beta }\left (\sqrt {3}\beta ^{2}\sqrt {\frac {1 }{\beta ^{3}}}+1\right ) ,q_{B,D}=\frac {1}{2\beta }\right ]\)
The only solution which satisfies the second order conditions and the feasibility conditions is \(\left [ q_{A,C}=\frac {1}{2\beta },q_{B,D}= \frac {1}{2\beta }\right ]\). The other roots are infeasible. They involve the merged firm capturing the entire market or the competitors capturing the entire market (Roots 1 and 5). They are “local maxima” due to the nature of profit functions but are not best responses. Roots 3 and 4 entail choices of negative quality. The equilibrium prices are \(\frac {1}{4\beta }\left (\beta +1\right )\) and the profits of the merged firm is \(\frac {1}{8}\) and of the competitors is \(\frac {1}{16}\).
Proof of Proposition 2
Because \(\frac {4}{25}>\frac {1}{8}\), a direct acquisition when variable costs are used to increase quality is strictly preferred to an indirect acquisition. The benefit of a direct acquisition is unrelated to β.
Proof of Corollary 1
The ordering of qualities post and pre-acquisition when \(\beta > \frac {\sqrt {2372 329}+503}{5220}\) is \(q_{direct\ acq}^{competitor}>q_{indirect\ acq}^{competitor}>q_{pre\ acq}>q_{indirect\ acq}^{merged\ firm}>q_{direct\ acq}^{merged\ firm}\). First, I let \({\Delta }_{1}=q_{direct\ acq}^{competitor}-q_{indirect\ acq}^{competitor}= \frac {1-}{2700\beta \left (145\beta -23\right ) \left (4\beta -1\right ) } 8669\beta +21 555\beta ^{2}+406\). The first term is positive in the allowable range for β and the second term is positive for all \(\beta > \frac {\sqrt {40 146 241}-8669}{43 110}\thickapprox -0.54\). Second, I let \({\Delta }_{2}=q_{indirect\ acq}^{competitor}-q_{pre\ acq}=\frac {5}{432\beta \left (4\beta -1\right ) }>0\). Third, I let \({\Delta }_{3}=q_{pre\ acq}-q_{indirect\ acq}^{merged\ firm}=\frac {1}{432}\frac {36\beta -5}{\beta \left (4\beta -1\right ) }>0\). Fourth, I let \({\Delta }_{4}=q_{indirect\ acq}^{merged\ firm}-q_{direct\ acq}^{merged\ firm}=\frac {1}{1350\beta \left (145\beta -23\right ) \left (4\beta -1\right ) }\left (-503\beta +2610\beta ^{2}-203\right )\). The first term is positive in the allowable range and the second term is a parabola which is positive for \(\beta >\frac {\sqrt {2372 329 }+503}{5220}\thickapprox 0.391 42\) and \(\beta <,\frac {503-\sqrt {2372 329}}{ 5220}\thickapprox -0.1987\).
Proof of Corollary 2
The gap between the merged firm and its competitors for a direct acquisition is \(Gap_{1}=\frac {11}{2\left (145\beta -23\right ) }\). The gap between the merged firm and its competitors for an indirect acquisition is \(Gap_{2}=\frac {1}{12\left (4\beta -1\right ) }\). \(Gap_{1}-Gap_{2}=\frac {1}{12} \frac {119\beta -43}{\left (145\beta -23\right ) \left (4\beta -1\right ) }>0\) for all \(\beta >\frac {43}{119}\thickapprox 0.361 34\) and the allowable zone is β > .36471.
Proof of Corollary 3
The average quality pre-acquisition is \(\overline {q}_{pre\ acq}= \frac {5}{48\beta }\), the average quality after a direct acquisition near firm is \(\overline {q}_{direct}= \frac {1}{100}\frac {1435\beta -228 }{\beta \left (145\beta -23\right ) }\) and the average quality after an indirect acquisition is \(\overline {q}_{indirect}= \frac {1}{216} \frac {81\beta -20}{\beta \left (4\beta -1\right ) }\). \(\overline {q}_{pre\ acq}-\overline {q}_{direct}=\frac {1}{1200}\frac {905\beta -139}{\beta \left (145\beta -23\right ) }>0\) for all \(\beta \gtrapprox 0.158 62\). \(\overline {q}_{direct}-\overline {q}_{indirect}=\frac {1}{5400}\frac {-7663\beta +16 335\beta ^{2}+812}{\beta \left (145\beta -23\right ) \left (4\beta -1\right ) }>0\) for all \(\beta >\frac {\sqrt {5665 489}+7663}{32 670} \thickapprox 0.307 41\) and the allowable zone is β > .36471.
Proof of Lemma 7
With fixed investments in quality, the expression for total welfare is as follows:
The benefit from consumption when all 4 firms operate is:
The transportation costs are as follows:
The investments in quality are:
As long as prices are equal, consumers will buy from the firm that offers the combination of quality and transportation cost that maximizes utility. Using the expressions from Table 1, I construct the function for W and optimize for the qualities. The first order conditions are:
The solution to these equations is \(q_{A}=q_{B}=q_{C}=q_{D}=\frac {1}{8\beta }\) and \(W_{all\ firms}=\frac {1}{16}\frac {-\beta +16v\beta +1}{\beta }\). Here, the central planner serves customers at all four locations, the optimal quality for the firms is \(\frac {1}{8\beta }\) and transportation costs are minimized. However, there are two discontinuous possibilities that need to be considered. First, the central planner could set high quality at one firm and 0 quality at the other firms: all consumers would travel to one firm to realize the benefit of high quality. Second, the central planner could set a high qualities at two firms located on opposite sides of the circular market, 0 quality at the other firms and have consumers travel to the firm that is closest.
-
1.
Option 1: Here one firm serves all consumers. I assume the firm that invests in quality is Firm A and consumers travel at most \(\frac {1}{2}\) to patronize Firm A. This implies that \(W_{one\ firm}=v-2{\int \limits }_{0}^{\frac {1}{2} }xdx+q_{A}-\beta {q_{A}^{2}}\). Optimizing with respect to qA, I obtain \(q_{A}=\frac {1}{2\beta }\). This leads to total welfare of \(\frac {1}{4}\frac { -\beta +4v\beta +1}{\beta }\).
-
2.
Option 2: Here, two firms serve all consumers and prices are fixed at 0. I assume the firms that invest in quality are Firms A and C. The indifference point between Firm A and C is given by \(x^{\ast }=\frac {1}{2} q_{A}-\frac {1}{2}q_{C}+\frac {1}{4}\). This implies that \(W_{two\ firms}=v+2x^{\ast }q_{A}+2\left (\frac {1}{2}-x^{\ast }\right ) q_{C}-2{\int \limits }_{0}^{x^{\ast }}xdx-2{\int \limits }_{x^{\ast }}^{\frac {1}{2}}\left (\frac {1 }{2}-x\right ) dx-\beta {q_{A}^{2}}-\beta {q_{C}^{2}}\). Substituting I have \(W= v+\frac {1}{2}q_{A}+\frac {1}{2}q_{C}+\frac {1}{2}{q_{A}^{2}}+\frac { 1}{2}{q_{C}^{2}}-q_{A}q_{C}-\beta {q_{A}^{2}}-\beta {q_{C}^{2}}-\frac {1}{8}\). Optimizing with respect to qA and qC, I obtain \(q_{A}=q_{C}=\frac {1 }{4\beta }\). This leads to total welfare of \(\frac {1}{8}\frac {-\beta +8v\beta +1}{\beta }\).
Straightforward calculations show that when β < 1, Wone firm > Wtwo firms > Wall firms and when β > 1, Wall firms > Wtwo firms > Wone firm.
Proof of Proposition 3
In order to determine total welfare pre-acquisition and for direct and indirect acquisitions, note that all firms realize positive demand. Hence, the indifferent points of Table 1 determine the transportation costs and benefit associated with consumption at each firm. Let W be total welfare in the market.
The basic benefit is v. The benefit created by quality when all 4 firms operate is:
The transportation costs are as follows:
The investments in quality are:
Simple substitution of the equilibrium values from Lemmas 3 and 4 yield the following expressions for Total Welfare.
We know from Lemma 3 that the allowable range is \(\beta >\frac {3\sqrt {43 849}+2439}{8410}\thickapprox .36471.\)
-
Step 1
I let Δ1 = Wpre−acquisition − Wdirect. This is positive when − 2100290β − 10961725β2 + 37845000β3 + 179171 > 0. The roots are too long for presentation but are approximately \(\left (-0.176 56,6. 720 5\times 10^{-2},0.399 \right )\). Only the third root lies in the feasible range, hence Δ1 > 0 when \(\beta \gtrapprox 0. 399\).
-
Step 2
I let Δ2 = Wdirect − Windirect. This is positive when 134588113β − 1450197016β2 + 7317382365β3 − 16068832650β4 + 12261780000β5 − 5877256 > 0. Solving the expression numerically, I find 5 roots: 2 are complex numbers 7.2044 × 10− 2 + 7.2629 × 10− 2i and 7.2044 × 10− 2 − 7.2629 × 10− 2i and three are real 0.21250, 0.36766 and 0.58624. Hence Δ2 > 0 when \(\beta \in \left (\thickapprox 0.367 66,\thickapprox 0.586 24\right ).\)
-
Step 3
I let Δ3 = Wpre−acquisition − Windirect. This is positive when − 1044β + 1944β2 + 115 > 0. The roots are \(\frac {29+ \sqrt {151}}{108}\thickapprox 0.382 30\) and \(\frac {29-\sqrt {151}}{108} \thickapprox\) 0.15474. Only the first root lies in the feasible range, hence Δ3 > 0 when \(\beta \gtrapprox 0.382 30\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Soberman, D. Business Expansion Through Acquisition. Cust. Need. and Solut. 9, 74–94 (2022). https://doi.org/10.1007/s40547-022-00131-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40547-022-00131-6