Dynamics of a Cracked Cantilever Beam Subjected to a Moving Point Force Using Discrete Element Method

Abstract

Purpose

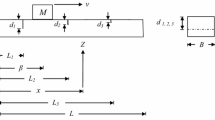
This work aims to investigate a cracked cantilever beam subjected to a moving point force using the Discrete Element Method (DEM).

Contribution and Method

A novel approach to mathematically include a moving force in discrete element formulation of a cracked beam is the main contribution of this paper. The local reduction in the stiffness of the cantilever beam due to the presence of a crack has been accounted for by a popularly used result from fracture mechanics. Hence, the present work provides an alternative approach to numerically evaluate the forced vibration of cracked beams under the application of a moving point force.

Conclusion

The methodology has been verified by comparing some of the results obtained here to those obtained using an already published analytical method. In the end, the effects of crack length, crack location, and force-velocity on the dynamic behavior of the cracked beam are studied using the proposed methodology. The proposed method can provide an effective alternative for the analysis of cracked beams subjected to a moving point force.

Appendix

A. Description of the Analytical Method used in this Work for Comparison with the DEM

The analytical method used in this work for comparison with the proposed numerical approach was presented by Lin et al. [25]. For the beam considered in Sect. 2, the analytical formulation will be presented in this section. The governing equation of the beam is derived by considering the beam to have two parts connected by a rotation spring at the crack location. The partial differential equations which model the vibration of the beam can be written as:

$$EI\frac{{\partial^{4} y_{i} \left( {x,t} \right)}}{{\partial x^{4} }} + \rho A\frac{{\partial^{2} y_{i} \left( {x,t} \right)}}{{\partial t^{2} }} = F_{0} \delta \left( {x - vt} \right){\text{ for }}x_{i - 1} < x < x_{i} , \, i = 1,2,$$

(18)

where $x_{0} = 0$, $x_{1} = L_{c}$, $x_{2} = L$, $y_{1}$ and $y_{2}$ are displacements in left and right sides of the crack, respectively, $I$ is the area moment of inertia about the centroidal axis of the beam cross section which is perpendicular to the $x$ axis and $A$ is the area of cross section. And the boundary conditions for the cantilever beam are given below [25]:

$$y_{1} \left( {0,t} \right) = 0,$$

(19)

$$\left. {\frac{{\partial y_{1} }}{\partial x}} \right|_{x = 0,t = t} = 0,$$

(20)

$$\left. {\frac{{\partial^{2} y_{2} }}{{\partial x^{2} }}} \right|_{x = L,t = t} = 0,$$

(21)

$$\left. {\frac{{\partial^{3} y_{2} }}{{\partial x^{3} }}} \right|_{x = L,t = t} = 0.$$

(22)

The continuity of displacement, shear force and bending moment at crack location can be written mathematically as [25]:

$$y_{1} \left( {L_{c}^{ - } ,t} \right) = y_{2} \left( {L_{c}^{ + } ,t} \right),$$

(23)

$$\left. {\frac{{\partial^{2} y_{1} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ - } ,t = t}} = \left. {\frac{{\partial^{2} y_{2} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ + } ,t = t}} ,$$

(24)

$$\left. {\frac{{\partial^{3} y_{1} }}{{\partial x^{3} }}} \right|_{{x = L_{c}^{ - } ,t = t}} = \left. {\frac{{\partial^{3} y_{2} }}{{\partial x^{3} }}} \right|_{{x = L_{c}^{ + } ,t = t}} ,$$

(25)

where $L_{c}^{ - }$ and $L_{c}^{ + }$ represent the location infinitesimally close to the crack from left and from right, respectively. Since the bending stiffness at the crack location has been reduced, there exists a discontinuity in the slope across the crack.

$$\left. {\left. {\frac{{\partial y_{2} }}{\partial x}} \right|_{{x = L_{c}^{ + } ,t = t}} - \frac{{\partial y_{1} }}{\partial x}} \right|_{{x = L_{c}^{ - } ,t = t}} = \psi L\left. {\frac{{\partial^{2} y_{2} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ + } ,t = t}} ,$$

(26)

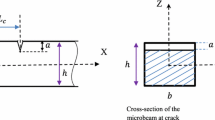
where $\psi = 6*\pi \left( \frac{a}{d} \right)^{2} \xi \left( \frac{a}{d} \right)\left( \frac{d}{L} \right)$ is known as non-dimensional crack sectional flexibility and for a single-sided open crack:

$$\xi \left( \frac{a}{d} \right) = 0.6384 - 1.035\frac{a}{d} + 3.7201\left( \frac{a}{d} \right)^{2} - 5.1773\left( \frac{a}{d} \right)^{3} + 7.553\left( \frac{a}{d} \right)^{4} - 7.332\left( \frac{a}{d} \right)^{5} + 2.4909\left( \frac{a}{d} \right)^{6} .$$

Eigensolutions of the Beam

To find the eigensolutions, $F_{0} \delta \left( {x - vt} \right)$ has to be set to zero in Eqs. (18). After that assuming the solutions of the form $y_{i} = w_{i} \left( x \right)e^{j\omega t}$, one gets the eigenvalue problem as:

$$\frac{{\partial^{4} w_{i} \left( x \right)}}{{\partial x^{4} }} - \lambda^{4} \frac{{\partial^{2} w_{i} \left( x \right)}}{{\partial t^{2} }} = 0\quad {\text{for }}x_{i - 1} < x < x_{i} ,$$

(27)

where

$$\lambda^{4} = \frac{{\omega^{2} \rho A}}{EI}.$$

(28)

The compatibility requirements from Eqs. (23) to (26) lead to:

$$w_{1} \left( {L_{c}^{ - } } \right) = w_{2} \left( {L_{c}^{ + } } \right),$$

(29)

$$\left. {\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ - } }} = \left. {\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ + } }} ,$$

(30)

$$\left. {\frac{{\partial^{3} w_{1} }}{{\partial x^{3} }}} \right|_{{x = L_{c}^{ - } }} = \left. {\frac{{\partial^{3} w_{2} }}{{\partial x^{3} }}} \right|_{{x = L_{c}^{ + } }} ,$$

(31)

$$\left. {\left. {\frac{{\partial w_{2} }}{\partial x}} \right|_{{x = L_{c}^{ + } }} - \frac{{\partial w_{1} }}{\partial x}} \right|_{{x = L_{c}^{ - } }} = \psi L\left. {\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }}} \right|_{{x = L_{c}^{ + } }} .$$

(32)

And the boundary conditions from Eqs. (19) to (22) lead to:

$$y_{1} \left( {0,t} \right) = 0, \to w_{1} \left( 0 \right) = 0,$$

(33)

$$\left. {\frac{{\partial y_{1} }}{\partial x}} \right|_{x = 0,t = t} = 0, \to \left. {\frac{{\partial w_{1} }}{\partial x}} \right|_{x = 0} = 0,$$

(34)

$$\left. {\frac{{\partial^{2} y_{2} }}{{\partial x^{2} }}} \right|_{x = L,t = t} = 0, \to \left. {\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }}} \right|_{x = L} = 0,$$

(35)

$$\left. {\frac{{\partial^{3} y_{2} }}{{\partial x^{3} }}} \right|_{x = L,t = t} = 0, \to \left. {\frac{{\partial^{3} w_{2} }}{{\partial x^{3} }}} \right|_{x = L} = 0.$$

(36)

The general solutions of Eq. (27) can be written as [25]:

$$w_{i} \left( x \right) = A_{i} \sin \lambda (x - x_{i - 1} ) + B_{i} \cos \lambda (x - x_{i - 1} ) + C_{i} \sinh \lambda (x - x_{i - 1} ) + D_{i} \cosh \lambda (x - x_{i - 1} ), \, x_{i - 1} < x < x_{i} .$$

(37)

Application of compatibility conditions gives the relationship between the arbitrary constants of each of the segments as:

$$\left\{ {\begin{array}{*{20}c} {A_{2} } \\ {B_{2} } \\ {C_{2} } \\ {D_{2} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {t_{11} } & {t_{12} } & \cdots & {t_{14} } \\ {t_{21} } & {t_{22} } & \cdots & \vdots \\ \vdots & \ddots & \ddots & \vdots \\ {t_{41} } & \cdots & {t_{42} } & {t_{44} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\} = \left[ T \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\}.$$

(38)

The elements of matrix $\left[ T \right]$ can be found in the appendix of [11]. Satisfaction of boundary conditions (33) and (34) gives:

$$\left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\} = \left[ P \right]_{2 \times 4} \left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}$$

(39)

And satisfying boundary conditions from Eqs. (35) and (36) and using Eq. (38) gives:

$$\left[ Q \right]_{2 \times 4} \left[ T \right]_{4 \times 4} \left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\},$$

(40)

where $\left[ Q \right]_{2 \times 4} = \left[ {\begin{array}{*{20}c} { - \sin \lambda \left( {L - L_{c} } \right)} & { - \cos \lambda \left( {L - L_{c} } \right)} & {\sinh \lambda \left( {L - L_{c} } \right)} & {\cosh \lambda \left( {L - L_{c} } \right)} \\ { - \cos \lambda \left( {L - L_{c} } \right)} & {\sin \lambda \left( {L - L_{c} } \right)} & {\cosh \lambda \left( {L - L_{c} } \right)} & {\sinh \lambda \left( {L - L_{c} } \right)} \\ \end{array} } \right].$ Eqs. (41) and (42) can be combined to get:

$$\left[ {\begin{array}{*{20}c} {\left[ Q \right]_{2 \times 4} \left[ T \right]_{4 \times 4} } \\ {\left[ P \right]_{2 \times 4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {B_{1} } \\ {C_{1} } \\ {D_{1} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}.$$

(41)

For non-trivial solutions of $\left( {A_{1} ,B_{1} ,C_{1} ,D_{1} } \right)$,$\det \left( {\left[ {\begin{array}{*{20}c} {\left[ Q \right]_{2 \times 4} \left[ T \right]_{4 \times 4} } \\ {\left[ P \right]_{2 \times 4} } \\ \end{array} } \right]} \right) = 0$, This provides the characteristic Eq. (42):

$$\begin{gathered} 2 - \psi \lambda_{n} \cos \lambda_{n} L_{c} \sinh \lambda_{n} L_{c} + \psi \lambda_{n} \cosh \lambda_{n} \left( {L - L_{c} } \right)\left( {\sin \lambda_{n} \left( {L - L_{c} } \right) + \cos \lambda_{n} L_{c} \cos \lambda_{n} \left( {L - L_{c} } \right)\sinh \lambda_{n} L_{c} } \right) \hfill \\ + \psi \lambda_{n} \cos \lambda_{n} \left( {L - L_{c} } \right)\sinh \lambda_{n} \left( {L - L_{c} } \right) + 2\cos \lambda_{n} L_{c} \cos \lambda_{n} \left( {L - L_{c} } \right)\sinh \lambda_{n} L_{c} \sinh \lambda_{n} \left( {L - L_{c} } \right) \hfill \\ - 2\sin \lambda_{n} L_{c} \sinh \lambda_{n} \left( {L - L_{c} } \right)\sinh \lambda_{n} L_{c} \sinh \lambda_{n} \left( {L - L_{c} } \right) \hfill \\ + \cosh \lambda_{n} L_{c} \left[ {\cosh \lambda_{n} \left( {L - L_{c} } \right)\left\{ {2\cos \lambda_{n} L - \psi \lambda_{n} \sin \lambda_{n} L} \right\}} \right] \hfill \\ + \cosh \lambda_{n} L_{c} \psi \lambda_{n} \left\{ {\sin \lambda_{n} L_{c} + \cos \lambda_{n} L_{c} \cos \lambda_{n} \left( {L - L_{c} } \right)\sin \lambda_{n} \left( {L - L_{c} } \right)} \right\} \hfill \\ = 0, \hfill \\ \end{gathered}$$

(42)

where $\lambda_{n}$ denote the nth eigenvalue of the system. To calculate corresponding $w_{n} \left( x \right)$ (i.e., the nth eigenfunction) first the constants $\left( {A_{1} ,B_{1} ,C_{1} ,D_{1} } \right)$ are calculated by substituting $\lambda_{n}$ in Eq. (41) and Eq. (38) is used to find the arbitrary constants $\left( {A_{2} ,B_{2} ,C_{2} ,D_{2} } \right)$. These sets of constants for different values of $\lambda_{n}$ can be substituted in Eqs. (37) to find the required eigenfunctions.

Forced Vibration Response of the Beam

The forced response of the system can now be determined by solving the Eq. (18) using the modal expansion theory. Equation (18) has been rewritten here:

$$EI\frac{{\partial^{4} y_{i} \left( {x,t} \right)}}{{\partial x^{4} }} + \rho A\frac{{\partial^{2} y_{i} \left( {x,t} \right)}}{{\partial t^{2} }} = F_{0} \delta \left( {x - vt} \right)\quad {\text{for }}x_{i - 1} < x < x_{i} , \, i = 1,2.$$

Expressing the forced response $y\left( {x,t} \right)$ as:

$$y\left( {x,t} \right) = \sum\limits_{j = 1}^{{N_{m} }} {w_{j} \left( x \right)q_{j} \left( t \right)} ,$$

(43)

where $w_{j} \left( x \right)$ are the eigenfunctions of the cracked beam and $q_{j} \left( t \right)$ are the generalized coordinates and $N_{m}$ is the number of eigenfunctions used for approximating the response.

Now substituting Eq. (43) in Eq. (18), taking the inner product with $w_{k} \left( x \right)$ and using the orthogonality property of eigenfunctions lead to:

$$\left( {\ddot{q}_{k} + \omega_{k}^{2} q_{k} } \right)\int\limits_{0}^{L} {\rho Aw_{k} \left( x \right)w_{k} \left( x \right)dx} = \int\limits_{0}^{L} {F_{0} \delta \left( {x - vt} \right)w_{k} \left( x \right)dx} .$$

(44)

Rearranging Eq. (44) with integral on the right hand side being simplified leads to:

$$\left( {\ddot{q}_{k} + \omega_{k}^{2} q_{k} } \right) = \frac{{F_{0} w_{k} \left( {vt} \right)}}{{\int\limits_{0}^{L} {\rho Aw_{k} \left( x \right)w_{k} \left( x \right)dx} }}.$$

(45)

Ordinary differential Eq. (45) can be solved for $q_{k}$ by using the Duhamel’s integral method and the solution can be written as:

$$q_{k} \left( t \right) = q_{k} \left( 0 \right)\cos \omega_{k} t + \frac{{\dot{q}_{k} \left( 0 \right)\sin \omega_{k} t}}{{\omega_{k} }} + \frac{1}{{\omega_{k} \int\limits_{0}^{L} {\rho Aw_{k} \left( x \right)w_{k} \left( x \right)dx} }}\int\limits_{0}^{t} {\sin \omega_{k} \left( {t - \tau } \right)F_{0} w_{k} \left( {v\tau } \right)d\tau } ,$$

(46)

where the eigenfunctions $w_{k} \left( {vt} \right)$ can be divided into two parts from Eq. (27) and can be written as:

$$\begin{gathered} w_{k} \left( {v\tau } \right) = f_{k1} \left( {v\tau } \right) = A_{k1} \sin \lambda_{k} (v\tau - x_{0} ) + B_{k1} \cos \lambda_{k} (v\tau - x_{0} ) + C_{k1} \sinh \lambda_{k} (v\tau - x_{0} ) \hfill \\ \, + D_{k1} \cosh \lambda_{k} (v\tau - x_{0} ),v\tau \le x_{1} {\text{ or }}\tau \le \frac{{x_{1} }}{v} \hfill \\ \, = f_{k2} \left( {v\tau } \right) = A_{k2} \sin \lambda_{k} (v\tau - x_{1} ) + B_{k2} \cos \lambda_{k} (v\tau - x_{1} ) + C_{k2} \sinh \lambda_{k} (v\tau - x_{1} ) \hfill \\ \, + D_{k2} \cosh \lambda_{k} (v\tau - x_{1} ),v\tau > x_{1} {\text{ or }}\tau > \frac{{x_{1} }}{v}. \hfill \\ \end{gathered}$$

Therefore, $q_{k} \left( t \right)$ can be determined and used in Eq. (43) along with $w_{k} \left( x \right)$ to get the final response $y\left( {x,t} \right)$.