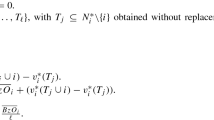Abstract
In several real data applications a biased sample arises naturally from the selection procedure. Recently, Economou et al. (Biom J 62: 238–249, 2020) used the concept of bivariate weighted distributions and proposed four different families of weight functions to describe cases in which the bias in a bivariate sample is caused by adopting sampling schemes that result in over- or under-representation of individuals with specific properties in the sample. The current paper focuses on revealing the contribution of each variable to the bias in the bivariate sample. More specifically, under the Bayesian perspective, Approximate Bayesian Computation methods are used to sample approximately from the posterior distribution, and the Deviance Information Criterion is employed to compare the fit of the models obtained by using different weight functions. The proposed method is illustrated to a real data set concerning NBA draft players.



Similar content being viewed by others
References
Afonso L, Corte Real P (2016) Using weighted distributions to model operational risk. ASTIN Bull 46(2):469–485
Arnold B, Nagaraja H (1991) On some properties of bivariate weighted distributions. Commun Stat Theory Methods 20(5–6):1853–1860
Berkson J (1946) Limitations of the application of fourfold table analysis to hospital data. Biom Bull 2:47–53
Celeux G, Forbes F, Robert CP, Titterington DM (2006) Bayesian Anal 1(4):651–673
Duong T, Goud B, Schauer K (2012) Closed-form density-based framework for automatic detection of cellular morphology changes. Proc Nat Acad Sci 109(22):8382–8387
Economou P, Batsidis A, Tzavelas G, Alexopoulos P (2020) ADNI: Berkson’s paradox and weighted distributions: An application to alzheimer’s disease. Bioml J 62:238–249
Economou P, Tzavelas G, Batsidis A (2020) Robust inference under r-size-biased sampling without replacement from finite population. J Appl Stat 47(13–15):2808–2824
Fisher R (1934) The effect of methods of ascertainment upon the estimation of frequencies. Ann Eugen 6(1):13–25
Geneletti S, Best N, Toledano MB, Elliot P, Richardson S (2013) Uncovering selection bias in case-control studies using Bayesian post-stratification. Stat Med 32:2555–2570
Greenland S (2003) Quantifying biases in casual models: classical confounding vs collider-stratification bias. Epidemiology 14:300–306
Gupta RC, Kirmani S (1990) The role of weighted distributions in stochastic modeling. Commun Statist 19(9):3147–3162
Hernan M, Hernandez-Diaz S, Robins J (2004) A structural approach to selection bias. Epidemiology 15:615–625
Jain K, Nanda A (1995) On multivariate weighted distributions. Commun Stat Theory Method 24(10):2517–2519
Kacprzak T, Herbel J, Amara A, Réfrégier A (2018) Accelerating approximate Bayesian computation with quantile regression: application to cosmological redshift distributions. J Cosmol Astropart Phys 2018(02):042
Kavetski D, Fenicia F, Reichert P, Albert C (2018) Signature-domain calibration of hydrological models using approximate Bayesian computation: theory and comparison to existing applications. Water Resour Res 54(6):4059–4083
McKinley T, Vernon I, Andrianakis I, McCreesh N, Oakley J, Nsubuga R, Goldstein M, White R (2018) Approximate Bayesian computation and simulation-based inference for complex stochastic epidemic models. Stat Sci 33(1):4–18. https://doi.org/10.1214/17-STS618
Nanda A, Jain K (1999) Some weighted distribution results on univariate and bivariate cases. J Stat Plan Inference 77(2):169–180
Navarro J, Ruiz J, Aguila YD (2006) Multivariate weighted distributions: a review and some extensions. Statistics 40(1):51–64
Patil G, Rao C (1978) Weighted distributions and size-biased sampling with applications to wildlife populations and human families. Biometrics 34(2):179–189
Pearl J (1995) Casual diagrams for empirical research. Biometrika 82(4):669–688
Rao C (1965) On discrete distributions arising out of methods of ascertainment. Sankhya Indian J Stat Ser A (1961–2002) 27(2/4):311–324
Raynal L, Marin J, Pudlo P, Ribatet M, Robert CP, Estoup A (2018) ABC random forests for Bayesian parameter inference. Bioinformatics 35(10):1720–1728
Richard L, Berg K, Thomas B (1994) Physical and performance characteristics of ncaa division i male basketball players. J Strength Cond Res 8(4):214–218
Rotnitzky A, Robins J (2005) Inverse probability weighted estimation in survival analysis. In: Encyclopedia of Biostatistics. Wiley, London
Samuelsen S, Anestad H, Skrondal A (2007) Stratified case-cohort analysis of general cohort sampling designs. Scan J Stat 343:103–119
Sarabia JM, Gomez-Deniz E (2008) Construction of multivariate distributions: a review of some recent results. SORT 32(1):3–36
Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A (2002) Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Stat Methodol) 64(4):583–639
Spirtes P, Glymour C, Scheines R (1993) Causation, prediction, and search. The MIT press, Cambridge
Tzavelas G, Douli M, Economou P (2017) Model misspecification effects for biased samples. Metrika 80(2):171–185
VanderWeel T, Herman M, Robins J (2008) Casual directed acyclic graphs and the direction of unmeasured confoundin bias. Epidemiology 19:720–728
Ziv G, Lidor R (2010) Vertical jump in female and male basketball players-a review of observational and experimental studies. J Sci Med Sport 13(3):332–9
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest:
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
In this Appendix the posterior density is reported for the general case and in detail for the special case of the application.
The likelihood function of a biased bivariate sample \(D = (x_j, y_j), j=1,\ldots ,n\) from a parent population with known pdf \(f(x,y;\theta )\) where \(\theta \) unknown parameters’ vector, when the bias in the sample is described by the weight function \(w_{i}(x,y;\theta ,\gamma _X,\gamma _Y)\) is
Let \(\pi (\zeta )\) be the joint prior density of the parameters of the model, where \(\zeta = (\theta , \gamma _X, \gamma _Y)\). Then, the posterior density of the model has the form:
Based on the discussion of Sect. 4.2, the joint distribution of height and the vertical jump in the population of interest is a bivariate normal. Moreover, independence of the parameters of the model is assumed and a prior distribution is adopted for each parameter \(\mu _X\), \(\mu _Y\), \(\sigma ^2_{X}\), \(\sigma ^2_{Y}\), \(\rho \), \(\gamma _X\) and \(\gamma _Y\). Then, the posterior density takes the form:
Using the priors described in Sect. 4.2 the following relation is obtained:
which can be expressed equivalently as
For the model \(\mathcal {M}_{1f}\), i.e., \(i=1\) and \(\gamma _X, \ \gamma _Y\) strictly positive, the posterior density has the form
Due to the posterior’s form direct sampling from it or even sampling from a standard MCMC method is not an easy task. Thus, ABC methods are used.
Rights and permissions
About this article
Cite this article
Economou, P., Batsidis, A., Tzavelas, G. et al. Understanding the Sampling Bias: A Case Study on NBA Drafts. J Stat Theory Pract 15, 45 (2021). https://doi.org/10.1007/s42519-021-00167-2
Accepted:
Published:
DOI: https://doi.org/10.1007/s42519-021-00167-2