Level-specific residuals and diagnostic measures, plots, and tests for random effects selection in multilevel and mixed models

Abstract

Multilevel data structures are often found in multiple substantive research areas, and multilevel models (MLMs) have been widely used to allow for such multilevel data structures. One important step when applying MLM is the selection of an optimal set of random effects to account for variability and heteroscedasticity in multilevel data. Literature reviews on current practices in applying MLM showed that diagnostic plots are only rarely used for model selection and for model checking. In this study, possible random effects and a generic description of the random effects were provided to guide researchers to select necessary random effects. In addition, based on extensive literature reviews, level-specific diagnostic plots were presented using various kinds of level-specific residuals, and diagnostic measures and statistical tests were suggested to select a set of random effects. Existing and newly proposed methods were illustrated using two data sets: a cross-sectional data set and a longitudinal data set. Along with the illustration, we discuss the methods and provide guidelines to select necessary random effects in model-building steps. R code was provided for the analyses.

Introduction

In multiple substantive research areas, data are often collected from clusters (e.g., Raudenbush & Bryk, 2002; Snijders & Bosker 1999). As an example, a random sample of hospitals (clusters) is selected, and then patients (observations) from the selected hospitals are randomly sampled. Furthermore, it is common to have a longitudinal design in which individuals (clusters) are observed over time (observations). To account for between-cluster variation, a multilevel model (MLM, e.g., Goldstein, 2003) has been widely applied. An MLM for continuous outcomes is also referred to as a random effect model (Laird & Ware, 1982), a hierarchical linear model (e.g., Bryk & Raudenbush, 1992), a linear mixed-effects model (LMM, e.g., McCulloch et al., 2008), a random regression model (Bock, 1983), or a random coefficient model (e.g., de Leeuw & Kreft, 1986; Longford1993).

In MLM specifications, the between-cluster variation is represented by random effects such as a random intercept and a random slope of a covariate. In the MLM literature, a quantity is considered random if it varies over clusters within a population, in which case the set of observed clusters can be interpreted as a random sample (e.g., Snijders & Bosker 1999, Section 4.2). The random intercept can be considered to model random variation across clusters, and the random slope can be used to model random variation of a covariate effect within the population of clusters. The primary interest of many MLM applications is in the estimation of fixed effects and their standard errors (Raudenbush & Bryk, 2002, p. 253), although we acknowledge that random effects (e.g., individual differences) can be of interest in other MLM applications. In many cases, the interest in random effects is auxiliary, to obtain accurate standard errors for the fixed effects. When necessary random effects are not included in MLM to model all sources of variability and heteroscedasticity in the data, standard errors of the fixed effects of interest are typically negative biased (see Longford 1993, pp. 53–56 for technical details). This bias leads to overestimating the statistical significance of the fixed effects.

Inclusion of a random intercept is often justified by a sufficiently large intraclass correlation (ICC, Shrout & Fleiss, 1979) based on an unconditional MLM (i.e., a random intercept model without any covariates). After including the random intercept, the next step is to investigate whether covariate effects need to be included, with a fixed effect and possibly with random effects as well (i.e., random slopes). In addition to the random intercept and random slopes, other kinds of random effects have been discussed to model heteroscedasticity (as described in detail below), although these random effects are rarely considered in practice. It is common to compare candidate models with different random effects (e.g., random intercept vs. random intercept-slope model) and to select a model based on likelihood ratio tests (LRT).¹

As a supplement to LRT in selecting random effects, diagnostic plots such as a residual plot, a scatter plot, and a normal probability plot can be used. These diagnostic plots can be used to explore missing random effects not captured by the model. For example, a scatter plot of residuals versus fitted values can be used to explore heteroscedasticity in residuals (variance changes within clusters). A non-random pattern in the plot such as a wedge-shaped pattern can be indicative of heteroscedasticity (e.g., Pinheiro & Bates, 2000, p. 341). In addition, the diagnostic plots can be used for assessing model assumptions in MLM such as homogeneity of residual variance, linearity, and normality of residuals. Model checking through diagnostic plots can be informative when selecting random effects. For instance, a diagnostic plot can be used to explore heteroscedasticity in residuals when considering adding a random effect to model heteroscedasticity. In the statistics literature for LMM, different kinds of residuals and diagnostic plots have been suggested for model selection and model checking (e.g., Galecki & Burzykowski, 2013, pp. 264–266, pp. 339–346; Pinheiro & Bates, 2000, Ch. 4). However, our literature review of current practices in using MLM shows that the diagnostic plots in selecting random effects and model checking are rarely used (also noted in Claeskens [2013, p. 442] and O’Connell et al., [2016, p. 99]).²

We identify the following problems in the current practices of using diagnostic plots mostly based on residuals for random effect selection in MLM applications in the social sciences. First, to the best of our knowledge, there are no publications in which an exhaustive list of random effects has been presented. It is not easy for substantive researchers to be aware of all possible random effects to be considered for model selection. Second, level-specific residuals have been developed in the statistics literature on LMM (Hilden-Minton, 1995; Loy & Hofmann, 2014; Pinheiro & Bates, 2000; Verbeke & Lesaffre, 1997) which have not been introduced in MLM textbooks for the social sciences (e.g., Goldstein, 2003; Hox, Moerbeek, & van de Schoot, 2018; Longford, 1993; Raudenbush & Bryk, 2002; Snijders & Bosker, 1999).³ Substantive researchers are not always aware of the available range of options. Third, the scaling of residuals (standardized vs. unstandardized) and the definitions of conditional vs. marginal residuals are possible sources of confusion. For example, Snijders and Bosker (1999, p. 129) suggested using unstandardized (individual-level) residuals to check the linearity effect of (an individual-level) covariate, whereas Hox, Moerbeek, and van de Schoot (2018) used standardized (individual-level) residuals to check the linearity. As far as we know, it has not been discussed what kind of residuals (e.g., unstandardized vs. standardized; conditional vs. marginal) should be used when. Fourth, many of the model diagnostics are graphical in nature, and interpretations of patterns in diagnostic plots can be subjective (McCullagh & Nelder, 1989, pp. 392–393). To enhance the detection of visual patterns in the diagnostic plots, it has been suggested to consider including smoothing functions in the plot (e.g., Snijders & Berkhof, 2007). For instance, the scatter plot of (individual-level) residuals versus a covariate can be smoothed using spline functions (Snijders & Bosker, 1999). However, statistical tests for the patterns are rarely conducted. To summarize, unanswered questions are (a) what kind of residuals should be used for different kinds of diagnostic plots when selecting all necessary effects and checking model assumptions (as information to select a set of the random effects), and (b) how should the visual patterns in the diagnostic plots be tested.

Purpose of the current study

The purpose of the current study is to overcome the problems we listed above. Specifically, first, possible random effects which can be included in the model are presented and a generic description of those random effects is provided. Second, an extensive literature review on residuals and diagnostic plots in LMM and MLM literature is conducted for model selection regarding random effects and for model checking. The review is based on four LMM texts (Faraway, 2016; Galecki & Burzykowski, 2013; Pinheiro & Bates, 2000; Verbeke & Molenberghs, 2000) and 9 MLM texts, handbooks, edited books, and book chapters (Finch, Bolin, & Kelley, 2014; Goldstein, 2003; Hox et al., 2018; Longford, 1993; Raudenbush & Bryk, 2002; Singer & Willett, 2003; Snijders & Bosker, 1999; Snijders & Berkhof, 2007; O’Connell, Yeomans-Maldonado, & McCoach, 2016). Third, specific kinds of residuals and diagnostic plots are presented to explore random effects and to check model assumptions, and inference methods are also presented to test patterns in diagnostic plots. Finally, in addition to diagnostic plots, we will also propose diagnostic measures to select an optimal set of random effects. All these proposed methods are presented and illustrated for a two-level design involving individual- and cluster-level units. Hereafter, we refer to the individual level as level 1 and the cluster level as level 2 throughout this paper. Generalizability to other multilevel designs will be discussed. Parameter estimation of MLMs is conducted using the popular nlme R package (Pinheiro, Bates, DebRoy, Sarkar, & R Core Team, 2020). We chose the nlme package because it allows all kinds of random effects we discussed in this paper to be modeled. The R code used in this paper is presented in Appendix A.

The rest of this paper is organized as follows. In “4 4”, we describe MLMs for cross-sectional and longitudinal data, list all kinds of random effects in MLM, and describe model-building steps. In “Illustrative data sets”, two empirical data sets are described for illustration. In “Level-specific residuals”, the literature review on the types of residuals in MLM is presented. In “4 4”, we suggest diagnostic measures, list diagnostic plots for random effect selection and model assumption checks, and discuss reasons for the kind of residuals to be used in diagnostic plots. In addition, we present statistical inference on patterns in the diagnostic plot. In “Illustration”, we illustrate the proposed methods using two empirical data sets. Finally, we end with a summary and a discussion.

Different kinds of random effects in multilevel models

In this section, we describe MLMs for cross-sectional and longitudinal data, list all kinds of random effects in MLM, and describe the model-building steps to be used in the selection of a set of random effects.

Multilevel models

An MLM with design matrices as in LMM is written as

$$ \mathbf{y}_{j}=\textbf{X}_{j}\boldsymbol{\beta} + \textbf{Z}_{j}\mathbf{b}_{j} + \boldsymbol{\epsilon}_{j}, $$

(1)

where j is an index for (non-overlapping) clusters; y_j is a vector of continuous responses; X_j is the design matrix of the fixed effects; Z_j is the design matrix of the random effects; β is the vector of fixed effects; b_j is the vector of random effects; and 𝜖_j is the vector of random residuals. The random effects are assumed to follow a multivariate normal distribution, $\textbf {b}_{j} \sim MVN(\textbf {0},{\Sigma })$, where Σ is a variance-covariance matrix of the random effects. In addition, the random residuals are assumed to follow a multivariate normal distribution, $\boldsymbol {\epsilon }_{j} \sim MVN(0,\mathcal {R}_{j})$. The residual variance-covariance matrices $\mathcal {R}_{j}$ can be decomposed into two independent components, a variance component (σ²) and a correlation component (R_j):

$$ \mathcal{R}_{j}=\sigma^{2}R_{j}. $$

(2)

For the cross-sectional data, the residual variance-covariance matrices are assumed to have a homoscedastic conditional independent structure:

$$ \mathcal{R}_{j}=\sigma^{2}R_{j}=\sigma^{2}\textbf{I}_{n_{j}}, $$

(3)

where n_j is the cluster size (i.e., the number of level-1 units within a cluster j). However, for the longitudinal data in which outcomes are collected repeatedly from the same individuals (i.e., clusters), it is common to model correlated errors (Galecki & Burzykowski, 2013; Pinheiro & Bates, 2000, Section 5.3.1; Verbeke & Lesaffre, 1997):

$$ \mathcal{R}_{j}=\sigma^{2}R_{j}=\sigma^{2}{\Lambda}_{j}\textbf{C}_{j}{\Lambda}_{j}, $$

(4)

where Λ_j is a diagonal matrix with nonnegative diagonal elements and C_j is a correlation matrix. The Λ_j allows for heteroscedasticity of observations within individual (cluster) j and C_j allows for correlation between the observations within the individual (Galecki & Burzykowski, 2013, p. 179). Various kinds of correlation matrices C_j can be specified for longitudinal data such as uniform correlation and correlations with an autoregressive (AR) component of order p and a moving average (MA) component of order q (ARMA(p,q)), or a continuous-time autoregressive process (Pinheiro & Bates, 2000).

The conditional distribution, f_y|b(y_j|b_j), of y_j given b_j is multivariate normal, with mean and variance written as:

$$ E(\textbf{y}_{j}|\mathbf{b}_{j})=\textbf{X}_{j}\boldsymbol{\beta} + \textbf{Z}_{j}\mathbf{b}_{j} $$

(5)

and

$$ Var(\textbf{y}_{j}|\mathbf{b}_{j})=\sigma^{2}R_{j}. $$

(6)

The marginal distribution, f_y(y_j), of y_j, is obtained by integrating out the random effects b_j from the joint distribution of y and b_j:

$$ f_{y}(\mathbf{y}_{j})=\int f_{y|b}(\mathbf{y}_{j}|\mathbf{b}_{j})f_{b}(\mathbf{b}_{j})d\mathbf{b}_{j}, $$

(7)

where f_y|b(y_j|b_j) is the conditional distribution and f_b(b_j) is the density of the unconditional distribution of b_j. The marginal distribution is also multivariate normal, with mean and variance written as:

$$ E(\mathbf{y}_{j})=\mathbf{X}_{j}\boldsymbol{\beta} $$

(8)

and

$$ Var(\mathbf{y}_{j})=\sigma^{2}V_{j}=\sigma^{2}\textbf{Z}_{j}D\textbf{Z}_{j}^{\prime} + \sigma^{2}R_{j}, $$

(9)

where D is the variance-covariance matrix of random effects, b_j.

Random effects in MLM

We will use different elements to describe different kinds of random effects: (a) data modes and (b) the unit of random effect, and (c) the unit of variation.

Data modes

Each of the levels in a multilevel structure is considered as a source of variation (Longford, 1993, p. 18). Data modes refer to kinds of units which may be a source of variation (Coombs, 1964). For example, students and schools are data modes and at the same time they are the levels in the two-level design in which students are nested within schools.

Unit of random effect and unit of variation

The unit of random effect (UR) is a covariate of a mode (e.g., students) which induces variation across the units of (mostly but not always) another mode (e.g., schools), denoted as unit of variation (UV ). For example, the gender of students (a covariate of students) may induce an effect that is random across schools (another mode than students). For the two-level data, the UR can be (a) all data entries (i.e., the 1-constant), (b) a level-1 covariate (x⁽¹⁾), and (c) a level-2 covariate (x⁽²⁾). The UV is the set of elements across which the random effect of the UR varies. The UV can be individuals (e.g., students) and clusters (e.g., schools) in cross-sectional two-level data, and time points (e.g., weeks or years) and individuals (e.g., students) in longitudinal two-level data. For example, age (UR) can vary across students (UV ). Together, the paired notions of UR and UV define a random effect. For notation, we propose UR|UV, inspired by random effect specifications in the lme4 (Bates, Maechler, Bolker, & Walker, 2015) and nlme R packages.

For two-level data as an example, there are four kinds of random effects:

• Random intercept: The effect of the 1-constant can vary across clusters at level 2 (e.g., schools in a cross-sectional design, individuals in a longitudinal design).

• Random slope: The effect of a level-1 covariate (x⁽¹⁾) varies across clusters at level 2.

• Random effects with different variances to model heteroscedasticity: In general, heteroscedasticity refers to the pattern in which the variability of a variable is unequal across the range of values of a second variable that explains or predicts it.

  • An effect of a level-1 covariate (x⁽¹⁾) can vary across units of level 1.

    Level-1 heteroscedasticity is heteroscedasticity of the random residuals (𝜖_j in Eq. 1). For a continuous level-1 covariate (x⁽¹⁾), the number of levels in the level-1 covariate should be less than the number of level-1 observations. For a categorial level-1 covariate (x⁽¹⁾), the variances of random residuals (σ²) are modeled depending on the level of the categorical level-1 covariate which allows for heteroscedasticity. For example, gender as a level-1 covariate can create heterogeneity in that the variance across individuals of one gender may be different from the variance across individuals of the other gender.

  • An effect of a level-2 covariate (x⁽²⁾) can vary across units of level 2 (i.e., clusters). As an example of heteroscedasticity, the variance of schools may be different depending on public vs. private as categories of a level-2 covariate.

Table 1 shows a list of all possible random effects in the two-level data, using our proposed notation UR|UV for random effects. For the two-level cross-sectional data, level 1 (observation level) refers to individuals (e.g., students) and level 2 (cluster level) refers to clusters (e.g., schools). As shown in Table 1 (top), the following kinds of random effects listed above are as follows:

• Random intercept: 1|clusters

• Random slope: x⁽¹⁾|clusters

• Random effects with different variances to model heteroscedasticity: Heteroscedasticity means that the variance of the random effects is allowed to differ depending on the values of the covariate in question.

  • The effect of a covariate at level 1 varies across level-1 observations: x⁽¹⁾|individuals

  • The effect of a covariate at level 2 varies across level-2 clusters: x⁽²⁾|clusters

Table 1 Different kinds of random effects in cross-sectional two-level data (top) and in longitudinal two-level data (bottom)

For the two-level longitudinal data, the level-1 units are time points and the level-2 units are individuals. As presented in Table 1 (bottom), the following kinds of random effects listed above are as follows:

• Random intercept: 1|individuals

• Random slope: x⁽¹⁾|individuals

• Random effects with different variances to model heteroscedasticity:

  • The effect of a covariate at level 1 varies across level-1 observations: x⁽¹⁾|time

  • The effect of a covariate at level 2 varies across level-2 clusters: x⁽²⁾|individuals

Model-building steps

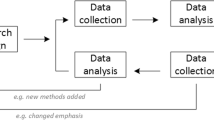
In the literature, it has been discussed how to proceed to check residuals. Either one starts with level 1 and continues to level 2 (i.e., upward approach, Pinheiro & Bates, 2000; Raudenbush & Bryk, 2002) or one starts from the highest level and continues with each subsequent lower level (i.e., downward approach, Langford & Lewis, 1998for outlier detection; Verbeke & Molenberghs, 2000). Snijders and Berkhof (2007) supported the upward approach for model assumption checking because level-1 residuals can be studied unconfounded by the higher-level residuals while the reverse is not possible (as noted in Hilden-Minton, 1995). However, the authors noted that checking level-2 outliers first is more efficient than checking level-1 outliers. Our reasoning behind this higher efficiency is that the number of clusters is smaller than the number of observations. It is inefficient to evaluate which level-1 units are outliers within a cluster that itself may be identified as a level-2 outlier. In our perspective, the argument of Hilden-Minton (1995) to work in the upward direction for residuals and the argument of Snijders and Berkhof (2007) to work downwards for outlier detection are persuasive. Thus, we take the upward approach for residual checking and the downward approach for outlier checking.

In MLM applications, necessary random effects are often selected in model building steps (e.g., Hox et al., 2018). As mentioned earlier, model checking through diagnostic plots can be informative when selecting random effects. In the following model-building steps, we discuss how both diagnostic plots and various tests of residuals can be used. The goal of model-building is to develop a parsimonious model that describes the data adequately while remaining interpretable. In the model-building steps below, we take a mixed approach including both (a) a confirmatory hypothesis testing for covariate(s) related to research questions and (b) an exploratory approach for the other covariates not related to the research questions.

• Step 0: A preliminary descriptive analysis is conducted without any modeling.

• Step 1: Random intercepts for the clusters are introduced as the only model component.

• Step 2: Fixed effects of level-1 covariates of interest are added to the random intercept model, such as the fixed effect of time in the longitudinal model. When the level-1 covariates are added to the random intercept model, level-1 linearity and level-1 heteroscedasticity can be explored. For the longitudinal data, correlated errors across time points can be investigated.

• Step 3: Random effects of level-1 covariates (i.e., random slopes) are added.

• Step 4: Fixed effects of level-2 covariates are added as well as their random effects (i.e., random effects to model level-2 heteroscedasticity).

• Step 5: A model with random effects and fixed effects of other covariates is selected based on goodness-of-fit criteria.

While building the model, we will keep track of outliers, influential points, and normality at level 1 and level 2, mostly through diagnostic plots and in some cases by using diagnostic measures we will introduce.

We suggest the following strategies, while going through the consecutive steps:

• From Step 2 to Step 4, outliers, influential points, and normality will be assessed to determine whether fixed and random effects of the model need to be included in the model.

• Outlying observations or clusters will not be removed before Step 4, because the outlying nature of an observation or cluster may change during the model building process. However, because outliers may have consequences for further steps, we will return to earlier steps after removing outliers.

• Non-normality will also be followed up in each step without making definite assessments until Step 4 is reached.

Illustrative data sets

We will use two empirical data sets in the following sections: a two-level cross-sectional data set and a two-level longitudinal data set, to illustrate level-specific diagnostic plots.

Example 1: two-level cross-sectional data (Math data)

A two-level cross-sectional data set was chosen from a popular MLM textbook (Kreft & de Leeuw, 1998; see pp. 58–60 for data description). It can be freely downloaded from http://www.bristol.ac.uk/cmm/learning/mmsoftware/data-rev.html. The dataset includes 519 students (level 1) nested within 23 schools (level 2) and an average cluster size of approximately 23. ICC was .243 (= 26.124/(26.124 + 81.244)), based on the unconditional random intercept model, which indicates that 24.3% of the total variation in math scores was explained by between-school variation. Rights (2019) considered the parents’ highest level of education (i.e., level-1 covariate $x_{ij}^{(1)}$) to predict math scores. As in Rights (2019), a goal of analysis in this paper is to predict math scores from parents’ highest level of education (called parentHED hereafter as a primary covariate; ranging from 1 to 6). Rights (2019) applied MLMs to the same dataset using random intercepts, random slopes, and a random effect for level-2 heteroscedasticity. As in Rights (2019), we consider the school-mean-centered parent education as a level-2 covariate ($x_{.j}^{(2)}$) and deviations of parent education from the level-2 covariate as a level-1 covariate ($x_{ij}^{(1)}-x_{.j}^{(2)}$) for an unconflated random slope and level-2 heteroscedasticity. In addition to parentHED as a primary covariate, level-1 covariates include socio-economic status of parents (ses), the number of hours of homework done per week (homework; ranging from 0 to 6), and a student ethnicity covariate (white; 1=white and 0=non-white) as level-1 control covariates. Additional level-2 covariates include education sector (public; 1=public and 0=private), the percentage of ethnic minority students in the school (percmin), and class size measured by the student-teacher ratio (ratio) as level-2 control covariates.

Example 2: Two-level longitudinal data (Hamilton depression [HD] data)

A longitudinal psychiatric data set was chosen, and the data set has been used to illustrate the application of MLM to longitudinal data (Hedeker, 2004). The data set can be freely downloaded from https://stats.idre.ucla.edu/r/examples/alda/r-applied-longitudinal-data-analysis-ch-7/. The data set is originally from a study described in Reisby et al., (1977). Reisby et al., (1977) investigated the longitudinal relationship between imipramine (commonly prescribed for the treatment of major depression) and desipramine plasma levels. The study included responses of the Hamilton depression (HD) rating scale (Hamilton, 1960) from 66 depressed inpatients. Lower HD scores indicate lower degrees of depression. Among the 66 depressed inpatients, 29 were diagnosed with a nonendogenous depression associated with tragic life events and 37 were diagnosed with an endogenous depression not associated with any specific event. This nonendogenous vs. endogenous group variable (Endog) is considered a level-2 covariate.

In the study of Reisby et al., (1977), patients received 225-mg/day doses of imipramine for four weeks, following 1 week with a placebo: week 0 (start of placebo week), week 1 (end of placebo week), week 2 (end of first drug treatment week), week 3 (end of second drug treatment week), week 4 (end of third drug treatment week), and week 5 (end of fourth drug treatment week). Patients were rated with the HD rating scale twice at week 0 (at the start and end of week 0) and at the end of each week during the four treatment weeks. In this longitudinal example, the level-1 covariate Week is a primary covariate and the level-2 covariate Endog is a control covariate. Forty-six of the 66 patients completed all responses at all time points, and the number of patients with complete responses at each week varied: 61 at week 0, 63 at week 1, 65 at week 2, 65 at week 3, 63 at week 4, and 58 at week 5. Patients with missing HD scores were omitted prior to analysis and only complete data were used. ICC due to clusters (i.e., patients) was 0.268 (= 13.929/(13.929 + 37.957)), based on an unconditional random intercept model (i.e., a random intercept model without any covariates). This indicates that 26.8% of repeated measures is explained by between-patient variation.

Level-specific residuals

A residual is defined as the difference between the observed value of the outcome variable and the fitted (or predicted) value: Residual = Observed - Fitted Value (or Predicted Value). A zero residual means that the selected model explains or predicts the observation exactly and non-zero residuals indicate model-data misfit. For MLM, residuals can be specified at each level of the multilevel data. Below, we describe various kinds of level-specific residuals.

Level-1 residuals

Ordinary least squares (OLS) regression for each cluster separately has been recommended for the analysis of level-1 residuals by Hilden-Minton (1995). In fitting separate OLS regression, random effects (random slopes) are treated as fixed effects so that the level-1 residuals can be inspected without being confounded by random effects and their underlying assumptions.

For the case in which one does not use OLS for each cluster, Hilden-Minton (1995) and Verbeke and Molenberghs (2000, pp. 151–152) defined two kinds of residuals in LMM:

• Conditional residuals: Conditional residuals are discrepancies between the observed and fitted values, and they indicate how much the observed values deviate from the predicted regression line for a cluster j $\tilde {\boldsymbol {\epsilon }}_{C.j}=\mathbf {y}_{j} - E(\mathbf {y}_{j}|\tilde {\mathbf {b}}_{j})=\mathbf {y}_{j}- \textbf {X}_{j}\widehat {\boldsymbol {\beta }} - \textbf {Z}_{j}\tilde {\mathbf {b}}_{j}$ Conditional residuals are obtained by conditioning on the random effects.

• Marginal residuals: Marginal residuals measure how a specific profile deviates from the estimated overall population mean, which means conditioning on the fixed effects only $\tilde {\boldsymbol {\epsilon }}_{M.j}=\mathbf {y}_{j} - E(\mathbf {y}_{j})=\mathbf {y}_{j}- \textbf {X}_{j}\widehat {\boldsymbol {\beta }}=\textbf {Z}_{j}\tilde {\mathbf {b}}_{j} + \tilde {\boldsymbol {\epsilon }}_{j}$ The marginal residuals include both the random effects and level-1 errors.

Hilden-Minton (1995) considers a residual to be confounded when it depends on errors other than the one that it is supposed to predict. Following this view, predicted conditional residuals ($\tilde {\boldsymbol {\epsilon }}_{C.j}$) are confounded because the conditional residuals are co-determined by the predicted random effects ($\tilde {\mathbf {b}}_{j}$) which themselves may deviate from the true random effects. That is, if the predicted random effects ($\tilde {\mathbf {b}}_{j}$) do not follow a normal distribution, the predicted conditional residuals ($\tilde {\boldsymbol {\epsilon }}_{C.j}$) may not follow a normal distribution even when the conditional residuals (𝜖_C.j) follow a normal distribution.

Residuals, whether conditional or marginal, can be raw residuals or transformed residuals. Based on all these distinctions, the following six types of residuals can be considered:

• Raw residuals

  • Conditional residuals: $\tilde {\boldsymbol {\epsilon }}_{C.j}$

  • Marginal residuals: $\tilde {\boldsymbol {\epsilon }}_{M.j}$

• Standardized (or Pearson or internally studentized) residuals: Scaling is implemented by using the estimated standard deviation of the corresponding residuals ($\widehat {\sigma }$).

  • Conditional residuals: $\frac {\tilde {\boldsymbol {\epsilon }}_{C.j}}{\widehat {\sigma }}$

  • Marginal residuals: $\frac {\tilde {\boldsymbol {\epsilon }}_{M.j}}{\widehat {\sigma }}$

• Independent residuals⁴: For LMM with correlations between residuals (level-1 error in longitudinal data), orthogonalization is suggested to obtain approximately independent residuals when the within-individual variance-covariance model can describe the level-1 error adequately (e.g., Galecki & Burzykowski, 2013, pp. 265–266). We assume that $\widehat {R}_{j}$ (the estimated correlation of the residuals) is an adequate description of the level-1 error. An adequate description is necessary to yield independent residuals (e.g., Galecki & Burzykowski, 2013, pp. 265–266).

  • Independent conditional residuals: The independent residuals can be calculated based on the Cholesky decomposition of the estimate of the residual variance-covariance matrix σ²R_j (Pinheiro & Bates 2000, p. 239). They can be calculated as $\tilde {\boldsymbol {\epsilon }}_{C.j}^{*}=(\widehat {\sigma }\widehat {U}_{C.j})^{-1}\tilde {\boldsymbol {\epsilon }}_{C.j}$, where $\widehat {U}_{C.j}^{\prime }\widehat {U}_{C.j}=\widehat {R}_{j}$.

  • Independent marginal residuals: The independent residuals can be calculated based on the Cholesky decomposition of the estimate of the marginal variance-covariance matrix σ²V_j (Schabenberger, 2004). They can be calculated as $\tilde {\boldsymbol {\epsilon }}_{M.j}^{*}=(\widehat {\sigma }\widehat {U}_{M.j})^{-1}\tilde {\boldsymbol {\epsilon }}_{M.j}$, where $\widehat {U}_{M.j}^{\prime }\widehat {U}_{M.j}=\widehat {V}_{j}$.

Standardization does not change the shape of the distribution (which is not necessarily normal), but the mean is transformed to a value of 0 and the standard deviation is transformed to a value of 1. We recommend using standardized residuals over unstandardized residuals because they are independent of the scale of the observations and are therefore easier to interpret.

For uncorrelated level-1 error models (e.g., the cross-sectional example data set), conditional standardized residuals are the same as conditional independent residuals, and marginal standardized residuals are the same as marginal independent residuals. For longitudinal data (e.g., the second example data set), level-1 errors are likely correlated because repeated measures are from the same individuals. For correlated level-1 error models mainly in longitudinal data analysis, standardized residuals are different from independent residuals. Because standard regression diagnostics are for independent residuals, we recommend using independent residuals for the correlated level-1 error models.

Random effects as level-2 residuals

The intercepts and slopes of level-1 covariates can vary across the clusters at level 2. These random coefficients are modeled as level-2 random effects and are considered level-2 residuals (e.g., Longford, 1993, pp. 60–61). The random effects (e.g., $\tilde {\textbf {b}}_{j}=[\tilde {b}_{0j},\tilde {b}_{1j}]'$, where $\tilde {b}_{0j}$ is the predicted random intercept and $\tilde {b}_{1j}$ is the predicted random slope) reflect how much specific profiles deviate from the population average profile (or discrepancies between expected values based on level-1 fixed effects and fitted values), $\tilde {\textbf {b}}_{j}=E(\mathbf {y}_{j}|\tilde {\mathbf {b}}_{j},\widehat {\boldsymbol {\beta }}) - E(\mathbf {y}_{j}|\widehat {\boldsymbol {\beta }})$.

The following kinds of level-2 residuals have been used:

• Empirical Bayes (EB) residuals: There are two main prediction methods for the random effects b (Snijders & Berkhof, 2007). The OLS method, which treats b as fixed effects, and the EB method, which estimates b as a conditional expectation given the data (y_j) and parameter estimates ($\widehat {\boldsymbol {\beta }}$). The relation between the level-2 predicted data ($\tilde {\mathbf {y}}_{j}=\frac {{\sum }_{i}\tilde {y}_{ij}}{n_{j}}$, where $\tilde {y}_{ij}$ is the level-1 predicted data and n_j is the number of individuals for a cluster j) and EB residuals is $\tilde {b}_{j} = \frac {n_{j}{\sigma _{b}^{2}}}{(n_{j}{\sigma _{b}^{2}} + \sigma ^{2})}\tilde {\mathbf {y}}_{j}$, where ${\sigma _{b}^{2}}$ is a variance of a random effect and σ² is a residual variance. The $\tilde {b}_{j}$ are called shrunken residuals because the EB ($\tilde {b}_{j}$) is shrunken with decreasing n_j (Goldstein, 2003, p. 22).

• Standardized EB residuals: Snijders and Berkhof (2007) define the standardized level-2 residuals as $\tilde {\textbf {b}}^{\prime }Cov(\tilde {\textbf {b}})^{-1}\tilde {\textbf {b}}$, where $Cov(\tilde {\textbf {b}})$ is the marginal sampling variance-covariance matrix.

What patterns in residuals indicate a good model?

For a model to be considered adequate, the following patterns should be observed in the level-specific residuals and a scatter plot of the residuals vs. fitted values:

• There should be no systematic trend in residuals.

• No more than approximately 5% of standardized residuals should have magnitudes greater than 1.96 (assuming that standardized residuals follow a standard normal distribution for a large sample size).

• The residuals should be randomly scattered around zero.

• The level-specific residuals should be normally distributed.

• The level-1 residuals (independent residuals for correlated level-1 error models in longitudinal data) should be independent of one another and independent of the fitted (predicted) values, $E(\mathbf {y}_{j};\widehat {\boldsymbol {\beta }},\tilde {\mathbf {b}}_{j})$.

Review of level-specific residuals in LMM and MLM literature

We reviewed 13 texts, handbooks, edited books, and book chapters in LMM and MLM literature to survey current practices of inspecting level-specific residuals. Table 2 presents a summary.⁵ As shown in Table 2, for level-1 residuals, conditional and marginal raw residuals, conditional standardized residuals, and conditional independent residuals have all been used in the LMM literature. However, in the MLM literature, only conditional raw and standardized residuals have been used. As also shown in Table 2 for random effects, unstandardized EB has been used in the LMM literature, and unstandardized and standardized EB have been used in the MLM literature.

Table 2 Uses of different residuals in LMM and MLM

Diagnostic measures, diagnostic plots, and statistical tests

In this section, we present diagnostic measures to select a set of random effects in model-building steps, level-specific diagnostic plots based on literature reviews, and statistical tests for patterns in the diagnostic plots.

Diagnostic measures

As a measure of difference between observed data and model predicted values (i.e., absolute fit), the root mean squared error (RMSE) is considered:

$$ \text{RMSE} = \sqrt{\frac{{\sum}_{i}{\sum}_{j}(\text{data}_{ij} - \text{fitted}_{ij})^{2}}{N}}, $$

(10)

where fitted values ($E(\mathbf {y}_{j};\widehat {\boldsymbol {\beta }}, \tilde {\mathbf {b}})$) are calculated based on the parameter estimates and predicted random effects from a selected model and N is the total sample size (calculated as N = n_jJ = nJ for a balanced design and $N={\sum }_{j=1}^{J}n_{j}$ for an unbalanced design). The RMSE is interpreted as the standard deviation of the part of the data unexplained by a model, (data_ij −fitted_ij). The normalized RMSE is the proportion of the RMSE related to the range of the outcome variable. Lower values of normalized RMSE indicate better model-data fit. Because it is easier to interpret, we suggest using the normalized RMSE to find an optimal set of fixed effects and to present a model-data fit measure for the selected model. The normalized RMSE can be obtained using the rmse(., normalized = TRUE) function from the performance package in R (Lüdecke, 2020).

In addition to the RMSE for the unexplained variance across the whole data set, we propose two measures for the level-1 unexplained variability and for exploring variability across clusters. They are based on the conditional (standardized) residuals per cluster:

• The median within-cluster semi-interquartile range of the residuals (median SIQR) across clusters. The smaller the median is, the better the model captures level-1 variability in the data.

• The SIQR of the within-cluster SIQRs (SIQR(SIQR)) across clusters. The smaller the SIQR(SIQR) is, the smaller the heteroscedasticity is. The median SIQR represents the unexplained variability within clusters and is robust against outliers, while the SIQR(SIQR) is a measure of heteroscedasticity and is robust against outlying within-cluster unexplained variability. The median and SIQR are used because they are less sensitive to outliers than the mean and standard deviation (SD).

Fixed effects of level-1 covariates are the major explanatory factors of within-cluster variation. However, when the linearity of the effects of level-1 covariates is violated, one can further reduce the variation of the residuals by adjusting for the effects for non-linear components. Thus, a substantial reduction of the median SIQR is a useful index for the inclusion of fixed effects of level-1 covariates and for investigating any non-linearity of such effects.

Random effects of level-1 covariates (i.e., random slopes) are an explanatory factor of differences in the variance within clusters (i.e., level-1 heteroscedasticity). A steeper slope can explain why a within-cluster variance is larger. If a covariate has a steeper slope in a cluster, the covariate has a stronger effect in that cluster, which implies more variation in the outcome variable (unless compensated by a smaller variation of the covariate). Random effects of level-2 covariates can explain differences in between-cluster variance (i.e., level-2 heteroscedasticity). Therefore, a substantial reduction of the SIQR(SIQR) is a useful index for the inclusion of random effects for level-1 and level-2 heteroscedasticity.

In addition to the median SIQR of the conditional (standardized) residuals per cluster, median SIQR can be calculated based on outcome variables to explore variability in the outcome variable. RMSE is a global measure obtained from various sources of variation, and therefore may be less sensitive to one specific source of variation. However, RMSE, which is calculated based on the variance of (data - fitted) may be oversensitive to outliers, whereas SIQR-based measures obtained with median and interquartile range are not. Therefore, we recommend the joint use of all three: RMSE, median SIQR, and SIQR(SIQR).

Diagnostic plots

Below, different kinds of diagnostic plots are discussed and organized by the model-building steps we introduced earlier. For each kind of diagnosis, we included reviews of the use of diagnostic plots in the LMM and MLM literature, summarized in Tables 3 and 4, respectively. Based on the literature reviews, commonly used diagnostic plots are selected in the model-building steps (Step 1 to Step 4). We will explain which residuals are most appropriate for each diagnostic plot when selecting random effects and which model assumptions can be checked. We use the Math data to illustrate diagnostic plots in each of the model-building steps (Step 0 to Step 4), except for a diagnostic plot of level-1 errors which is only used for the longitudinal data. For this diagnostic plot of the level-1 error, the HD data were used for illustration. In this section we present the different kinds of plots without making any model selection decisions for the Math data. As mentioned earlier, checking level-specific outliers, influential points, and normality can be implemented in Step 2 to Step 4 (which will be illustrated in the subsequent section.) However, we will wait with diagnostic plots for checking outliers, influential points, and normality until after other plots are presented from Step 0 to Step 4.

Table 3 Uses of diagnostic plots using residuals in LMM texts

Table 4 Uses of diagnostic plots using residuals in MLM texts, handbooks, edited books, and book chapters

Diagnostic plots in Step 0: A preliminary descriptive analysis without any modeling

In Step 0, we consider two plots: (a) a scatter plot of an outcome variable vs. a primary covariate (related to a research question) and (b) a scatter plot of an outcome variable vs. median SIQR to explore variability in the outcome variable across clusters.

A main research question for the Math data is the relationship between the math scores and the parents’ highest level of education (parentHED). Thus, the scatter plot of the math scores vs. parentHED is considered. As shown in Fig. 1 (Step 0 (a)), there appears to be an approximately linear relationship between the math scores and parentHED. To explore variability across clusters (i.e., schools) in the math scores, SIQR of the conditional standardized residuals was calculated for each of the clusters, and a scatter plot of the math scores vs. SIQR was made.⁶ As presented in Fig. 1 (Step 0 (b)), the SIQR varies with the math score, suggesting that the variability of math scores should be modeled as a function of the level of math scores in a cluster.

Fig. 1

Diagnostic plots for random effects selection in model-building steps

Diagnostic plots in Step 1: Random intercept for the clusters

To investigate the necessity of including a random intercept, box plots of conditional raw residuals have been considered by Pinheiro and Bates (2000, p. 138). In the box plots, we suggest using conditional standardized residuals to aid interpretability of the scale because the estimated standard deviation can be different depending on the scale of the covariates. Grouping of residuals by cluster can be indicative of a random intercept because they indicate between-cluster differences and thus within-cluster dependency.

Using the Math data, the following two models with and without a random intercept were fit:

$$ y_{ij} = \beta_{0} + \epsilon_{ij} $$

(11)

and

$$ y_{ij} = \beta_{0} + b_{0j} + \epsilon_{ij}. $$

(12)

Standardized residuals of the null model (11) and conditional standardized residuals of the random intercept model (12) were calculated. In Fig. 1 (Step 1 (a)), the residuals for the same cluster tend to have the same sign, showing dependency within clusters. After including a random intercept, the mean of the residuals for clusters tends to be closer to 0 (presented by the horizontal line in Step 1 (b) of Fig. 1) than before. As a way to quantify dependency in outcomes due to clusters, the ICC was also calculated using the random intercept model. The ICC value of .243 confirms the dependency and validates the inclusion of a random intercept.

Diagnostic plots in Step 2: Fixed effects of level-1 covariates.

When the level-1 covariates are added to the random intercept model, level-1 linearity and level-1 heteroscedasticity can be explored using diagnostic plots. We checked the linearity of level-1 covariate effects prior to investigating heteroscedasticity to meet the assumption that the expected value of the residuals was 0 (Snijders & Berkhof, 2007, pp. 148–149). If the assumption is not valid, the interpretation of heteroscedasticity may be incorrect.

Level-1 linearity

A scatter plot of level-1 residuals vs. level-1 covariate is commonly used to explore the level-1 linearity. The level-1 covariate has been plotted against different kinds of the level-1 residuals in the literature: marginal unstandardized (raw) residuals (Galecki & Burzykowski, 2013), conditional unstandardized residuals (Snijders & Berkhof, 2007; Snijders & Bosker, 1999), and conditional or marginal residuals (O’Connell et al., 2016).⁷ We recommend using standardized residuals to aid interpretability of the scale. In addition, we suggest using marginal level-1 residuals instead of conditional level-1 residuals because the marginal level-1 residuals include all sources of variability (random effects and level-1 errors) for the relation between the level-1 covariate and outcomes (note that the marginal level-1 residuals are residuals obtained after only removing the fixed effects rather than after removing the random effects as well) (Santos Nobre and da Motta Singer, 2007). When the assumption of level-1 linearity holds, the average of the marginal standardized level-1 residuals is close to 0 and no systematic patterns in the residuals are found.

For parentHED ($x_{ij}^{(1)}$) as a continuous covariate in Math data, level-1 linearity was investigated based on standardized marginal residuals for a model with a random intercept and a linear level-1 covariate ($x_{ij}^{(1)}-x_{.j}^{(2)}$) effect:

$$ y_{ij} = \beta_{0} + \beta_{1}(x_{ij}^{(1)}-x_{.j}^{(2)}) + b_{0j} + \epsilon_{ij}. $$

(13)

Marginal standardized residuals were calculated and plotted against the level-1 covariate. As shown in Fig. 1 (Step 2 (a)), it appears that there was a slight cubic polynomial pattern (which will be tested using statistical tests in the illustration section).

Level-1 heteroscedasticity

The most commonly used plot to explore level-1 heteroscedasticity is a scatter plot of residuals vs. fitted values ($E(\mathbf {y}_{j};\widehat {\boldsymbol {\beta }},\tilde {\mathbf {b}})$). Examples include conditional unstandardized (raw) residuals vs. fitted values (Faraway, 2016) and conditional standardized residuals vs. fitted values (Hox et al., 2018; Goldstein, 2003; Pinheiro & Bates, 2000). We recommend using standardized residuals for interpretability. In addition, we recommend using conditional level-1 residuals because they include only the unexplained variance and level-1 heteroscedasticity would show as unexplained variance. To check for level-1 heteroscedasticity, we explore whether the average of the conditional standardized level-1 residuals is close to 0 ($E(\tilde {\boldsymbol {\epsilon }}_{C.j}/\widehat {\sigma })=0$) and whether there is a constant variance across clusters ($Var(\tilde {\boldsymbol {\epsilon }}_{C.j}/\widehat {\sigma })=\sigma ^{2}$).

Using the Math data, conditional standardized residuals were calculated based on the random intercept model with a level-1 covariate (13). Fig. 1 (Step 2 (b)) presents possible level-1 heteroscedasticity. In the figure, the means of the conditional standardized residuals appear to be close to 0. However, the variance of the conditional standardized residuals looks different across the range of fitted values.

Level-1 error for longitudinal data

For longitudinal data, AR and MA can be explored using an autocorrelation function of the conditional standardized residuals from a fitted model (Pinheiro & Bates, 2000, p. 242⁸). Use of the marginal residuals was advocated by Lesaffre and Verbeke (1998) to investigate a within-person variance-covariance matrix ($Var(\mathbf {y}_{j})=\sigma ^{2}V_{j}=\sigma ^{2}\textbf {Z}_{j}D\textbf {Z}_{j}^{\prime } + \sigma ^{2}R_{j}$ [where D is the variance-covariance matrix of random effects, b_j]). We also recommend using marginal residuals because they include the random effects necessary to investigate whether the assumed covariance structure of the data (V ar(y_j)) does indeed fit the data. In addition, we suggest using standardized residuals for interpretability. Autocorrelations will be non-zero only in the presence of MA in the autocorrelation function (e.g., Chatfield, 2004). Fig. 1 (Step 2 (c)) presents the autocorrelation function of the marginal standardized residuals using the HD data.

A model can be selected among candidate models with differing C_j in Eq. 4 based on model selection methods, the Akaike information criterion (AIC, Akaike, 1974) and the Bayesian information criterion (BIC, Schwarz, 1978). When the correlated level-1 error model is selected, conditional or marginal independent residuals are recommended in the following steps to have approximately independent residuals, as residuals corrected for correlated level-1 errors. For example, after modeling the level-1 error regarding AR and MA, we recommend presenting an autocorrelation function of the marginal independent residuals to check whether there are noticeable patterns in the plot.

Diagnostic plot in Step 3: Random effects of level-1 covariates (i.e., random slopes) are added

The most common diagnostic plot to explore random slopes is OLS regression coefficients per cluster (Hox et al., 2018; Kreft & de Leeuw, 1998; Pinheiro & Bates, 2000; Raudenbush & Bryk, 2002; Snijders & Berkhof, 2007). In the plot, cluster-to-cluster variability in the OLS intercepts across clusters is indicative of a random intercept and cluster-to-cluster variability in the OLS slope of a level-1 covariate across clusters is indicative of a random slope. Figure 1 (Step 3 (a)) shows 23 OLS regression lines (one for each school) in Math data, which suggests that the slope (and intercept) differs across schools.

Diagnostic plots in Step 4: Fixed effects of level-2 covariates are added

In Step 4, the potential inclusion of level-2 covariates, level-2 linearity, and level-2 heteroscedasticity can be explored. In all plots listed below, standardized EB residuals are recommended for interpretability.

Potential inclusion of level-2 covariate

A scatter plot of unstandardized EB of random slope vs. a potential level-2 covariate (which is not included in the model yet) has been used to identify the functional form of the relationship between the potential level-2 covariate and the variable of interest (Raudenbush & Bryk, 2002, p. 269; Snijders & Berkhof, 2007, p. 133). Systematic patterns in the plot support the inclusion of the level-2 covariate in the model.

To illustrate this scatter plot, standardized EB of random slope was calculated based on the following model for the Math data with the cluster-mean-centered parentHED as the level-1 covariate:

$$ y_{ij} = \beta_{0} + \beta_{1}(x_{ij}^{(1)}-x_{.j}^{(2)}) + b_{0j} + b_{1j}(x_{ij}^{(1)}-x_{.j}^{(2)}) + \epsilon_{ij}. $$

(14)

Standardized EB of the random slope was plotted against the potential level-2 covariate, $x_{\cdot j}^{(2)}$ (the cluster mean of parentHED), as shown in Fig. 1 (Step 4 (a)). In the figure, the standardized EBs tended to be large in the middle range of $x_{.j}^{(2)}$, which may support the inclusion of $x_{.j}^{(2)}$.

Level-2 linearity

A scatter plot of unstandardized EB of random slope vs. level-2 covariates has been used to check the adequacy of the structure of those level-2 covariates (Raudenbush & Bryk, 2002, pp. 269–270). When the linear relationship between a level-2 covariate and the slope holds, the EB of the level-2 random slope should be randomly dispersed around 0 along the full range of the level-2 covariate.

To illustrate this scatter plot, standardized EB of random slope was calculated based on the following model:

$$ y_{ij} = \beta_{0} + \beta_{1}(x_{ij}^{(1)}-x_{.j}^{(2)}) + \beta_{2}x_{.j}^{(2)} + b_{0j} + b_{1j}(x_{ij}^{(1)}-x_{.j}^{(2)}) + \epsilon_{ij}. $$

(15)

The standardized EB of the random slope was plotted against the included level-2 covariate, $x_{.j}^{(2)}$. As shown in Fig. 1 (Step 4 (b)), the standardized EB does not seems to be random around 0, which may indicate that the level-2 linearity assumption may not hold.

Level-2 heteroscedasticity

A scatter plot of unstandardized EB of the random intercept (i.e., the level-2 residuals) vs. the level-2 covariate has been used to investigate the level-2 heteroscedasticity (Rights, 2019; Pinheiro & Bates, 2000, p. 189). In the plot, level-2 heteroscedasticity is checked by exploring whether the between-group variance depends on the level-2 covariate. Differences in the variance as a function of the level-2 covariate indicates heteroscedasticity. Standardized EB of the random intercept was calculated based on Eq. 15. In Fig. 1 (Step 4 (c)), it can be observed that variability differed depending on the level of the level-2 covariate, indicating the existence of level-2 heteroscedasticity.

For the following plots illustrating level-specific outliers, influence points, and normality, level-1 residuals and standardized EB were calculated based on a random intercept model (Equation 12) using Math data:

Diagnostic plots for outliers

There are two categories of outlier detection methods for LMM. The first category is a set of univariate outlier detection methods such as detection based on z-scores of the outcome variable and the IQR at each level of multilevel data. The second category is a multivariate method such as Mahalanobis distance (Mahalanobis, 1936). As reviewed in Table 5, Mahalanobis distance has mostly been used at level 2. In this paper, we use the univariate outlier detection method because of its simple calculation using level-specific residuals.

Table 5 Diagnostic plots

Level-1 outliers

The following plots can be used to detect outliers at level 1: (a) residuals vs. fitted values based on a selected model (e.g., O’Connell et al., 2016) and (b) box plot of conditional unstandardized residuals. For the plots (a) and (b), we recommend using conditional standardized residuals for uncorrelated level-1 error models and using conditional independent residuals for correlated level-1 error models (in longitudinal data). In plot (a), dispersed points in the plot can be identified as outliers. In plot (b), outliers can be detected based on the IQR. For the Math data, level-1 outliers were not detected as shown in Fig. 2 (outlier, Level 1) because there were no points outside of the whiskers.

Fig. 2

Diagnostic plots for outliers, influential points, and normality checks

Level-2 outliers

The following plots can be used to detect outliers at level 2: (a) A normal probability plot of unstandardized EB for random effects (Galecki & Burzykowski, 2013, p. 344; Longford, 1993). In the normal probability plot, the data are plotted against a theoretical normal distribution. In the plot, clusters which deviate from the straight line indicate outliers. Similar to the boxplots used for level-1 outlier detection, (b) box plots of standardized EB can also be used to detect Level-2 outliers. In the box plot, outliers can be detected for clusters outside of the whiskers. Again, we recommend using standardized EB for interpretability of the plots (a) and (b). For the Math data, there was one cluster at the lower end which deviates extremely from the straight line in the normal probability plot as shown in Fig. 2 (outlier, Level 2 (a)). In addition, the same cluster was outside of the whiskers in the box plot, Fig. 2 (outlier, Level 2 (b)).

Diagnostic plots for influential points

The Cook’s distance for each observation (Cook, 1977) is often calculated to detect influential data points. Cook’s distance of an observation is defined as the squared standardized difference between the estimates obtained with and without the observation in question, with large values suggesting possible influential data points. Demidenko and Stukel (2005) presented a Cook’s distance for LMM.

Level-1 influential points

The influence of an observation on parameter estimates is examined by leaving out each level-1 observation in turn and by recomputing parameter estimates. Because Cook’s distance is in the metric of an F(p,N − p) distribution (where p is the number of regression parameters excluding the intercept and N is the number of observations), the median point, F_0.5(p,N − p), is used as a cut-off value to detect influential points (e.g., Bollen & Jackman, 1990). As another cut-off value, level-1 observations can be considered as highly influential points when the level-1 Cook’s distance is larger than 1 for a large sample size (Cook & Weisberg, 1982). In this study, we use the cut-off value of 1 for the level-1 Cook’s distance because the number of observations is often large in multilevel data. For the Math data, there were no influential points at level 1 because there were no points with a Cook’s distance larger than the cut-off value of 1 (see Fig. 2 [influ. points, Level 1 (a)]).

Level-2 influential points

At level 2, the influence of a cluster on parameter estimates is examined by leaving out each cluster in turn and by recomputing parameter estimates. To our knowledge, a theoretical justification of a cut-off value has not been proposed for the level-2 Cook’s distance. In practice, a cut-off value of 4 divided by the number of clusters has been used to identify level-1 influence points if the sample size is not very large (e.g., 4059 individuals in Loy & Hofmann, 2014). We also use the cut-off value of 4 divided by the number of clusters. For the Math data, there were two influential points at level 2 (clusters), based on a cut-off value of .17 (= 4/23) (see Fig. 2 [influ. points, Level 2 (a)]).

Diagnostic plots for normality

Level-1 normality The following approaches have been used to check normality of level-1 residuals: (a) normal probability plots for various types of residuals such as conditional unstandardized residuals (Faraway, 2016; Pinheiro & Bates, 2000), unstandardized EB conditional residuals (Longford, 1993), conditional standardized residuals (Finch et al., 2014; Galecki & Burzykowski, 2013; Goldstein, 2003; Hox et al., 2018; Snijders & Bosker, 1999), and conditional independent residuals (Galecki & Burzykowski, 2013); (b) a scatter plot of conditional standardized residuals vs. level-1 covariate by group with a limited number of categories (Galecki & Burzykowski, 2013, p. 231); and (c) histograms overlaid with a curve based on conditional standardized residuals (Finch et al., 2014), conditional unstandardized residuals (Longford, 1993) and conditional or marginal standardized residuals (O’Connell et al., 2016). The normal probability plot (plot (a)) is created with an independent residual assumption. Thus, for level-1 correlated errors, we recommend using conditional independent level-1 residuals to obtain approximately independent residuals for the normal probability plot. However, it is not necessary to use the independent residuals for plots (b) and (c) because of their descriptive purpose. In the plots (b) and (c), standardized residuals are recommended for interpretability. For level-1 uncorrelated errors, standardized residuals are the same as independent residuals. Conditional residuals can be used in all three kinds of plots, and they are preferred over marginal residuals because in the conditional residuals both fixed and random effects of the model are accounted for. In the plot (a), straight lines indicate normality. In the plot (b), the normality assumption seems reasonable when there are no conditional standardized residuals (presented on the y-axis) smaller than the 1st percentile of the standard normal distribution (− 2.33) or larger than the 99th percentile of the standard normal distribution (2.33) for a level-1 covariate (on the x-axis) by groups. In the plot (c), normality can be assumed when the shape of the distribution in the histogram looks like the overlaid normal (or bell-shape) distribution.

The plots (a) and (c) are illustrated using the Math data. The plot (b) is not applicable to the data because there are too many levels of the level-1 covariate. As shown in Fig. 2 (normality, Level 1), small deviations from normality were observed in the middle and toward the ends of the distributions of the conditional standardized residuals.

Level-2 normality

The following plots have been used for checking normality of random effects: (a) normal probability plots of unstandardized EB (Faraway, 2016; Galecki & Burzykowski, 2013; Goldstein, 2003; Longford, 1993; Pinheiro & Bates, 2000; Snijders & Bosker, 1999) or standardized EB residuals (Snijders & Berkhof, 2007) and (b) histograms of unstandardized EB residuals (O’Connell et al., 2016; Verbeke & Molenberghs, 2000). Mainly unstandardized EB has been used in the plots, except in one case where a normal probability plot of standardized EB is used in Snijders and Berkhof (2007). We recommend using standardized EB for interpretability. For the Math data, deviations from normality were observed at the ends of distributions of the standardized EB in both plots, as shown in Fig. 2 (normality, Level 2).

Statistical tests

Interpreting patterns in diagnostic plots is subjective in nature. Thus, in this subsection, we provide statistical tests for a more objective interpretation.

Testing for randomness in residuals

Bartels (1982) proposed a rank version of the von Neumann’s (1941) ratio test to test the null hypothesis that there is randomness in data against the alternative hypothesis that there is trend in the data. Bartels ratio test statistic is defined as

$$ T=\frac{{\sum}_{i=1}^{I-1}(r[i]-r[i+1])^{2}}{{\sum}_{i=1}^{I}(r[i]-\bar{r})^{2}}, $$

(16)

where i is an index for level-1 observations (i = 1,…,I), r[1],…,r[I] are ranks of the level-1 residuals $\tilde {\epsilon }_{1},\ldots ,\tilde {\epsilon }_{I}$ in the diagnostic plots, and $\bar {r}$ is the average rank based on the number of residuals, (I + 1)/2. The Bartels ratio test can be used to test whether there is trend in the residuals of a selected model.

Testing for autocorrelations in residuals

After modeling level-1 correlated errors in longitudinal data, the Durbin-Watson test (Durbin and Watson, 1950) can be used to test the null hypothesis of independent level-1 residuals against first-order serially correlated errors. The Durbin-Watson test statistic is defined as

$$ DW=\frac{{\sum}_{i=2}^{I}(\tilde{\epsilon}_{i}-\tilde{\epsilon}_{i-1})^{2}}{{\sum}_{i=1}^{I}\tilde{\epsilon}_{i}^{2}}, $$

(17)

where $\tilde {\epsilon }_{i}$ is a calculated residual based on data, parameter estimates, and predicted random effects.

Testing for homogeneity of variance across groups

There are various tests to test the homogeneity of variance in residuals across groups defined by one or more factors as in an analysis of variance (ANOVA) (see Wang et al., 2016 for reviews). In this study, Levene’s test (Levene et al., 1960) was selected as a commonly used test in social and behavioral sciences (e.g., SPSS software, which uses Levene’s test as the default). Wang et al., (2016) showed via simulation studies that the Levene’s test maintained adequate Type I error rates and power in various conditions. When the number of levels for the level-1 and level-2 covariates is small, Levene’s test can be used to test level-1 and level-2 homogeneity, respectively. In addition, Levene’s test can be used to test whether the variance of residuals differs across clusters to confirm the necessity of including a random intercept.

Testing for smooth functions in the diagnostic plots

Smooth functions can be plotted to observe patterns in the diagnostic plots, such as plotting level-1 (marginal standardized) residuals vs. level-1 covariate for testing level-1 linearity (Fig. 1 [Step 2 (a)]), level-1 (conditional standardized) residuals vs. fitted values for testing level-1 heteroscedasticity (Fig. 1 [Step 2 (b)]), standardized EB of the random intercept vs. level-2 covariate for testing level-2 linearity (Fig. 1 [Step 4 (b)]), and standardized EB of the random slope vs. level-2 covariate for testing level-2 heteroscedasticity (Fig. 1 [Step 4 (c)]).

The univariate smooth function f_h(x) of a covariate x is a weighted sum of a set of basis functions defined over the covariate x:

$$ f_{h}(x) = \sum\limits_{k=1}^{K}\gamma_{hk}b_{hk}(x_{h}), $$

(18)

where k is an index for a basis function (k = 1,…,K), x_h is a covariate for a smooth function h, γ_hk is a basis coefficient, and b_hk(x) is the k th basis function for smooth function h. Because the f_h(x) can be confounded with the intercept, a model is estimated with an identification constraint that the sum of the function f_h over the observed covariate values is 0 (i.e., ${\sum }_{v} f_{h}(x_{hv}) = 0$ for each h with v as a subscript for observations). For the univariate smooth function (f_h(x)), a cubic regression spline (CRS, Wood, 2017) and a thin plate regression spline (TPRS; Wood, 2017, 5.5.1) are commonly used splines that can be implemented using the mgcv R package (Wood, 2019).

To test whether a smooth function f_h(x) is distinguishable from zero, the following null hypothesis can be tested: H₀ : f_h(x) = 0 for all x in the range of interest. A test statistic for f_h is

$$ T_{r}=\widehat{\mathbf{f}}_{h}^{\prime}\mathbf{V}_{f_{h}}^{-}\widehat{\mathbf{f}}_{h}, $$

(19)

where r is the rounded effective degrees of freedom (edf ) of f_h and $\mathbf {V}_{f_{h}}^{-}$ is a rank r pseudo-inverse of $\mathbf {V}_{f_{h}}$ calculated as $XV_{\boldsymbol {\gamma }}X^{\prime }$ (where X are basis functions and V_γ is the variance-covariance matrix for $\widehat {\boldsymbol {\gamma }}$). Each $\widehat {\mathbf {f}}_{h}$ is approximately multivariate normal,

$$ \widehat{\mathbf{f}}_{h} \sim MVN(\mathbf{f}_{h},\mathbf{V}_{f_{h}}), $$

(20)

where f_h is the vector of f_h(x) evaluated at the observed covariate values. Under H₀, the test statistic T_r follows a Chi-square distribution ($T_{r} \sim {\chi _{r}^{2}}$) with r = edf (Wood, 2012). When H₀ is rejected, one can conclude that there is a pattern (linear or nonlinear) in the data or residuals. The edf can be referred to when investigating whether the relation between a covariate and the outcome (e.g., residuals) is linear or nonlinear (Wood, 2017). The higher the edf, the wigglier the estimated smooth function is. An edf of 1 indicates a linear effect of a covariate on the outcome, an edf of 2 indicates an approximately quadratic effect of a covariate on the outcome, and an edf of 3 indicates an approximately cubic effect of a covariate on the outcome. Smooth functions have confidence intervals, which are obtained by taking the quantiles from the posterior distribution of the f_h (Marra and Wood, 2012).

Normality

The normality assumption of level-1 residuals and univariate EB (in our case, EB of the random intercept) can be tested using the Shapiro–Wilk normality test. When a selected model includes more than one random effect (e.g., random intercept and random slope), the multivariate normality of the random effects can be tested. A multivariate normality test such as Mardia’s test can be considered to test the multivariate normality assumption of the random effects (e.g., see Farrell, Salibian-Barrera, & Naczk, 2007; von Eye & Bogat, 2004, for the details of the test).

Illustration

In this section, uses of diagnostic plots based on level-specific residuals, diagnostic measures, and statistical tests of the patterns in the diagnostic plots are illustrated in a model-building strategy using cross-sectional and longitudinal empirical data sets. R code is provided for each step in Appendix A.

Example 1: Two-level cross-sectional data (Math data)

Steps 0 and 1 (A Preliminary Descriptive Analysis and Random Intercepts for the Clusters) and their results are discussed and reported earlier (see the Diagnostic Plots subsection). Below, Steps 2–5 are illustrated. Table 6 presents a summary of analyses and results.

Table 6 Summary of analyses and results for Math data

Step 2. Fixed effects of the level-1 covariate of interest

As mentioned earlier, a goal of analysis using the math data set is to predict math scores from parents’ highest level of education (parentHED). In Step 2, the fixed effect of the level-1 covariate of interest, the cluster-mean-centered parentHED ($x^{(1)}_{ij} - x^{(2)}_{\cdot j}$), is added to create Model 1:

$$ y_{ij} = \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + \epsilon_{ij}, $$

(21)

where β₁ is the fixed effect of the cluster-mean-centered parentHED. The addition of the fixed effect of the level-1 covariate lowered the median SIQR from 0.790 in the Null Model Random to 0.679 in Model 1. This result indicates that Model 1 better captured the level-1 variability in the data than Null Model Random.

Level-1 linearity

Cluster-mean-centered parentHED was plotted against the marginal standardized residuals obtained from Model 1 to examine whether the relationship between cluster-mean-centered parentHED and math scores is strictly linear. As shown in Fig. 3 (Step 2 (a)), there is a nonlinear relationship between the cluster-mean-centered parentHED and the marginal standardized residuals at the extreme values of the cluster-mean-centered parentHED, indicating that $(x^{(1)}_{ij} - x^{(2)}_{\cdot j})$ may have a non-linear (square and/or cubic) relationship with math scores. To test these higher-degree effects of $(x^{(1)}_{ij} - x^{(2)}_{\cdot j})$ on math scores, an alternative version of Model 1 including the square and cubic effects of $(x^{(1)}_{ij} - x^{(2)}_{\cdot j})$ called Model 1a, was tested:

$$ \begin{array}{@{}rcl@{}} y_{ij} &=& \beta_{0j} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + \beta_{2}(x^{(1)}_{ij} - x^{(2)}_{\cdot j})^{2}\\ && + \beta_{3}(x^{(1)}_{ij} - x^{(2)}_{\cdot j})^{3} + \epsilon_{ij}, \end{array} $$

(22)

where β₁, β₂, and β₃ are the linear, square, and cubic (respectively) fixed effects of the cluster-centered parentHED. Neither of the higher order (square and cubic) terms in Model 1a were found to be statistically significant, having p values of .2397 and .4529, respectively. In addition, a smooth curve fitted to predict marginal standardized residuals of Model 1 as a function of cluster-centered parentHED (using the mgcv package in R) showed that a smooth curve is not needed (F = 1.627, edf = 10.6, p value= .077). Based on these results, linearity was assumed, and Model 1 was used instead of Model 1a, with only the linear term for $(x^{(1)}_{ij} - x^{(2)}_{\cdot j})$ included.

Fig. 3

Diagnostic plots for random effects selection in the two-level cross-sectional data (Math data)

Level-1 heteroscedasticity

The fitted values of Model 1 were plotted against the conditional standardized residuals to explore the level-1 heteroscedasticity, as presented in Fig. 3 (Step 2 (b)). The conditional standardized residuals were distributed around 0 along the continuum of fitted values, meaning that homoscedasticity can be assumed. In addition, a Levene’s test showed that the conditional standardized residuals were not significantly heteroscedastic (p value= .098).

Level-2 outliers

If any level-1 or level-2 units are detected during the model building process (up to Step 4) as being both outlying and influential, these level-1 and/or level-2 units will be removed from the data, as they are expected to influence the resulting parameter estimates in a way that disagrees with the rest of the data (Hilden-Minton, 1995; Langford & Lewis, 1998). To detect level-2 outliers, a normal Q-Q plot of the standardized EB of the intercept for Model 1 was plotted against a theoretical normal distribution in Fig. 3 (Step 2 (c)). The standardized EB of the intercept were largely normal, with no standardized EB falling outside of the 95% confidence bands. The standardized EB of the intercept for all level-2 units ranged from -1.665 to 2.253. Based on these results, no level-2 units were considered to be outliers.

Level-2 influential points

There were two level-2 influential points, having Cook’s distances exceeding the cutoff of 0.1739 = 4/23 for a sample size of 23 schools, as shown in Fig. 3 (Step 2 (d)).

Level-1 outliers

To detect level-1 outliers, the fitted values from Model 1 were plotted against the conditional standardized residuals (see Fig. 3 [Step 2 (e)]). No outliers were detected as having unusually high conditional standardized residuals. The largest observed conditional standardized residual was 2.751, which although large is not unexpected given the large number of level-1 units (519).

Level-1 influential points

No level-1 influential points were detected, as no point had a Cook’s distance greater than the cut-off value of 1 in Fig. 3 (Step 2 (f)). The highest Cook’s distance detected was 0.0195.

Level-1 normality

A normal Q-Q plot as presented in Fig. 3 (Step 2 (g)) was generated to examine whether the conditional standardized residuals of Model 1 were normally distributed. The Q-Q plot shows that the conditional standardized residuals were mostly normal, with some deviations from normality in the lower extreme (with conditional standardized residuals falling slightly outside the 95% confidence bands). A Shapiro–Wilk test indicated that conditional standardized residuals were significantly non-normal (p value = .0022), which as shown in the normal Q-Q plot above is due to deviances from normality in the extreme observations. However, a histogram of conditional standardized residuals of Model 1 overlaid a normal curve shows that this deviance from normality is not large (see Fig. 3 [Step 2 (h)]). To conclude, level-1 normality was assumed because, although the p value was small, the deviance from normality was too small to give up on the normality assumption.

Level-2 normality

A normal Q-Q plot was generated to examine whether the standardized EB of the intercept of Model 1 were normally distributed, as presented in Fig. 3 (Step 2 (c)).

Step 3. Random effects of the level-1 covariate of interest

In this step the random effect (i.e., random slope) of the level-1 covariate ($x^{(1)}_{ij} - x^{(2)}_{\cdot j}$), the cluster-mean-centered parentHED, is added to the Null Model Random (Equation 12) to create Model 2:

$$ y_{ij} = \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + b_{1j}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + \epsilon_{ij}, $$

(23)

where b_1j is the random slope of the cluster-mean-centered parentHED. The addition of the random effect of the level-1 covariate lowered the median SIQR from 0.679 in Model 1 to 0.627 in Model 2, but it increased the SIQR(SIQR) from 0.121 in Model 1 to 0.143 in Model 2. These results indicate that Model 2 better captured the level-1 variability in the data (by having a smaller median SIQR), but was slightly more heteroscedastic (by having a larger SIQR(SIQR)). The small difference in SIQR(SIQR) is likely influenced by the small number of level-2 units, as will be discussed in Step 5.

To show the variability in the effect of $x^{(1)}_{ij} - x^{(2)}_{\cdot j}$ across schools, the ordinary least squares (OLS) regression line predicting math scores with cluster-mean-centered parentHED was plotted for each school, as shown in Fig. 3 (Step 3 (a)). Variability in intercepts across schools in this plot is indicative of the need for a random intercept (b_0j), whereas variability in slopes across schools in this plot is indicative of the need for the random slope (b_1j).

Level-1 heteroscedasticity and level-specific outliers, influential points, and normality

As in Step 2, level-1 heteroscedasticity, level-1 and level-2 outliers and influential points, and level-1 normality were checked by examining the conditional standardized residuals and standardized EB of the intercept of Model 2. In addition, level-2 normality and multivariate normality were checked by examining the standardized EB of the intercept and slope of Model 2.

The conditional standardized residuals of Model 2 were distributed around 0 along the continuum of fitted values, indicative of level-1 homoscedasticity. This was further supported by a Levene’s test showing that the conditional standardized residuals were not significantly heteroscedastic (p value = .139). One level-1 outlier was detected with a conditional standardized residual of 2.797, though no level-1 units (including this outlier) were influential, with a maximum Cook’s distance of 0.0229. One influential level-2 unit was detected with a Cook’s distance of 0.237 (> 0.174), though no level-2 outliers were detected, with all standardized EB of the intercept ranging from -1.615 to 2.352. A normal Q-Q plot of the conditional standardized residuals of Model 2 (plotted to evaluate level-1 normality) resulted in a pattern similar to Model 1. As a result, level-1 normality is assumed for Model 2.

Normal Q-Q plots were generated to examine whether the standardized EB of the intercept and slope were normally distributed for Model 2 (the figure is not shown). The standardized EB of the intercept were normally distributed, with all standardized EB falling within the 95% confidence bands. The standardized EB of the slope were mostly normally distributed, with two level-2 units falling outside the 95% confidence bands. To further examine level-2 normality, histograms of the standardized EB of the intercept and slope were plotted (the figure is not shown). In both cases, level-2 normality was questionable to investigate, as any potential non-normality could be the result of the small number of level-2 units (23). Because there were no drastic violations of level-2 normality (and no exceptional outliers observed), level-2 normality was assumed for Model 2.

Step 4. Fixed effects of a level-2 covariate of interest

In this step the fixed effect of the level-2 covariate $x^{(2)}_{\cdot j}$, the cluster mean of parentHED, was added to create Model 3:

$$ y_{ij} {=} \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + b_{1j}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + \beta_{2}x^{(2)}_{\cdot j} + \epsilon_{ij}, $$

(24)

where β₂ is the fixed effect of the cluster mean of parentHED.

Potential inclusion of level-2 covariate

To explore whether the parentHED cluster means should be included in the model, the level-2 covariate (which was not previously included) was plotted vs. the standardized EB of the random slope for Model 2 (Equation 23, which does not include the level-2 covariate), as presented in Fig. 3 (Step 3 (a)). Standardized EB of the random slope had an identifiable pattern (a negative linear trend) across the range of parentHED cluster means, justifying the inclusion of the cluster mean of parentHED in the model. After including the cluster mean of parentHED in the model, the standardized EB of the random slope for Model 3 was plotted (see Fig. 3 [Step 4 (b)]). Although there was still a negative linear trend in the standardized EB, the slope of this negative trend was reduced from − 0.6035 (in Model 2) to − 0.3132 (in Model 3).

Level-2 linearity

To examine whether the relationship between the included parentHED cluster means and math scores is strictly linear, a scatter plot of the standardized EB of the random slope for Model 3 vs. the level-2 covariate was generated (see Fig. 3 [Step 4 (c)]). The standardized EB were not randomly dispersed around 0 along the full range of the level-2 covariate, as would be expected if the relationship between parentHED cluster means and math scores was nonlinear. Instead, there was a significantly negative linear trend (slope = − 0.313, p value= .0337). In addition, a third-degree smooth curve fitted to predict standardized EB as a function of parentHED cluster means (using the mgcv package in R) was found to be significantly nonlinear (F = 3.545, edf = 1.720, p value = .0325), which suggests that there is a nonlinear relationship that needs to be included in the model. As Fig. 3 (Step 4 (c)) shows, there is a potentially nonlinear relationship between parentHED cluster means and math scores in Model 3, indicating that parentHED cluster means may have a non-linear (square and/or cubic) relationship with math scores. To test higher-degree effects of parentHED cluster means on math scores, an alternative version of Model 3 including the square and cubic effects of parentHED cluster means ($x^{(2)}_{\cdot j}$) on math scores, called Model 3a, was tested:

$$ \begin{array}{@{}rcl@{}} y_{ij} &=& \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + b_{1j}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) \\ &&+ \beta_{2}x^{(2)}_{\cdot j} + \beta_{3}(x^{(2)}_{\cdot j})^{2} + \beta_{4}(x^{(2)}_{\cdot j})^{3} + \epsilon_{ij}, \end{array} $$

(25)

where β₂, β₃, and β₄ are the linear, square, and cubic (respectively) fixed effects of parentHED cluster means on math scores. Both of the higher-order (square and cubic) terms in Model 3a were statistically significant (p value= .0255 and p value= .0282, respectively). A scatter plot of the level-2 covariate vs. the standardized EB of the random slope for Model 3a was generated to compare with Model 3 (the figure is not shown.) The pattern observed for Model 3a was almost identical to that observed for Model 3 without the inclusion of the higher-order terms of parentHED cluster means. These results indicate that the original pattern observed in the plot of the level-2 covariate vs. the standardized EB of the random slope for Model 3 was not caused by a strong nonlinear relationship between math scores and parentHED cluster means. Because the number of level-2 units is small (23), it is possible that the results stem from a few clusters. The negative slope and the nonlinearity may have been caused by two clusters with more negative standardized EB (− 1.970 and − 1.451) than the rest of the clusters. To examine this possibility, the level-2 covariate vs. the standardized EB of the random slope for Model 3 was plotted without these two clusters, as presented in Fig. 3 (Step 4 (d)). The standardized EB without these two clusters were much more consistently centered around 0 along the full range of the level-2 covariate, with a nonsignificantly positive intercept (intercept = 0.056, p value= .858) and nonsignificantly positive slope (slope = 0.036, p value= .727). Based on these results, it is likely that the pattern observed was caused by the two clusters, rather than being a systematic pattern in the data indicative of level-2 nonlinearity. In addition, Model 3 had a smaller RMSE (0.2028) than Model 3a (0.2033), and Model 3 fits better than Model 3a based on BIC and AIC (BIC= 3628.188 for Model 3 vs. BIC= 3772.394 for Model 3a; AIC= 3598.728 for Model 3 vs. AIC= 3739.928 for Model 3a). Taking all of these results together, we considered Model 3 to be preferable to Model 3a. Going forward, Model 3 is used (rather than Model 3a) throughout the model-building process.

Level-2 heteroscedasticity

To explore the level-2 heteroscedasticity, a scatter plot of the standardized EB of the random intercept for Model 3 vs. the level-2 covariate was generated (see Fig. 3 [Step 4 (e)]). A Levene’s test (F(21,1) = 249.4, p value= .050) suggests that the variance of the standardized EB is constant along the full range of parentHED cluster means (indicative of level-2 homoscedasticity).

Level-2 outliers

To detect level-2 outliers, a normal probability plot of standardized EB for the random intercept was plotted against a theoretical normal distribution (the figure is not shown). One cluster at the lower end deviated extremely from the line in the normal probability plot. This cluster can also be observed as an outlier of the box plot of standardized EB (the figure is not shown). Similar plots were created with standardized EB for the random slope. In the normal probability and box plots, there were two deviate clusters.

Level-2 influential points

There were two level-2 influential clusters, having Cook’s distances of 0.261 and 0.319, exceeding the cutoff of 0.174 = 4/23 for a sample size of 23 schools (the figure is not shown). One of these influential clusters (having a Cook’s distance of 0.261) was also the level-2 outlier observed. Because this cluster drastically differs from the rest of the data and is expected to influence parameter estimates, this cluster was removed from the data. Although a second cluster was found to have an influence on parameter estimates (having a Cook’s distance of 0.319), it was not found to be an outlier. This means that this cluster is expected to influence parameter estimates in agreeance with the rest of the data, and as a result it is not necessary to remove this cluster from the data.

Outlier removal

Because this is the final step of the model-building procedure regarding random effects, the single level-2 outlying cluster was removed from the data. The level-2 outlying cluster contained 19 level-1 units, meaning that the resulting data set after removing this outlier contained 500 (519 - 19) level-1 units and 22 (23 - 1) level-2 clusters.

A second iteration of Steps 1–4 was made with this reduced data set. There were a few differences in the results of Steps 1–4 in this second iteration. First, no level-1 outliers were detected in Step 3 (as opposed to the single level-1 outlier previously detected). Second, the higher-order (square and cubic) terms in Model 3a in Step 4 were no longer significant (p value = .1496 and p value = .1887, respectively). Third, two level-2 influential points were detected in Step 4, having Cook’s distances of 0.208 and 0.387, exceeding the cutoff of 0.182 = 4/22 for a sample size of 22 schools. However, neither of these level-2 units were found to be outliers, meaning that these clusters are expected to influence parameter estimates in agreeance with the rest of the data, and as a result their removal from the data was not necessary. Fourth, several median SIQR and SIQR(SIQR) values, as well as the ranking of these values across models, differed between the two iterations. These differing median SIQR and SIQR(SIQR) values are presented and discussed below.

Level-2 normality

Normal Q-Q plots were generated to examine whether the standardized EB of the intercept and slope for Model 3 were normally distributed (the figure is not shown). The standardized EB of the intercept were normally distributed, with all standardized EB falling within the 95% confidence bands. The standardized EB of the slope appeared non-normal, with four level-2 units falling outside the 95% confidence bands at the lower extreme. To further examine level-2 normality, histograms were plotted for the standardized EB of the intercept and slope (figures are not shown). The outlying standardized EB of the slope at the lower extreme likely appear to be outliers due to the small number of level-2 units (22, after the outlying level-2 unit was removed). The four smallest standardized EB of the slope ranged from -1.968 to -0.4438, which although not large in magnitude were considered outlying in the normal Q-Q plot because the other 19 standardized EB of the slope ranged from − 0.1533 to 0.8252. Because these outlying standardized EB of the slope were not drastically large in magnitude, and the potential level-2 non-normality observed is explainable by the small number of level-2 units, level-2 normality was assumed for Model 3.

Level-1 outliers, level-1 influential points, and level-1 normality

Similar plots were created to explore level-1 outliers, influential points, and normality as shown in Step 2. To detect any outliers, the fitted values from Model 3 were plotted against the conditional standardized residuals. No level-1 outliers were detected as having unusually high conditional standardized residuals. The largest observed conditional standardized residuals were − 2.751 and 2.704, which although large in magnitude are not unexpected given the large number of level-1 units (519). In addition, no level-1 influential points were detected, as no point had a Cook’s distance greater than the cut-off value of 1. The highest Cook’s distance detected was 0.01655.

Diagnostic measures and model selection from Steps 1–4

In Table 7, the three diagnostic measures considered for comparing models are RMSE, median SIQR, and SIQR(SIQR), in addition to AIC and BIC. Based on the AIC and BIC presented in Table 7, Model 3 was selected as the best-fitting model regarding the level-1 and level-2 fixed and random effects of parentHED. These results agree with the analyses in Step 4 illustrating the importance of the level-2 covariate of parentHED cluster means, a parameter which was only included in Model 3. This added complexity of Model 3 was motivated by AIC and BIC, which still ranked Model 3 as the best model despite the penalization for a larger number of parameters. The only diagnostic measures for which Model 3 did not outperform the other models was in median SIQR and SIQR(SIQR). Model 3 had similar median SIQR to both Model 1 and Model 2, indicating that these three models all captured the level-1 variability in the data about equally well. Model 3 had the highest SIQR(SIQR) of the four models, indicating that Model 3 had the highest heteroscedasticity of the four models.⁹

Table 7 Model comparisons regarding diagnostic measures of Math data

The conditional standardized residuals of Model 3 had no noticeable systematic trend, with residuals scattered uniformly around zero. The lack of a systematic trend in residuals is indicative of Model 3 adequately estimating math scores without omitting a critical fixed or random effect. A Bartels ratio test conducted on the conditional standardized residuals of Model 3 showed that residuals were not significantly nonrandom (T = 0.0823, n = 500, p value= .5327). Histograms of the level-1 conditional standardized residuals, the level-2 standardized EB of the random intercept, and the level-2 standardized EB of the random slope for Model 3 were plotted to evaluate the normality of residuals (see Fig. 3 [Step 5 (a)]). The level-1 conditional standardized residuals are clearly normally distributed, and based on Shapiro’s test the conditional standardized residuals are not significantly non-normal (p value = .0936). The small number of level-2 units makes it difficult to visually determine if the level-2 standardized EB of the random intercept and of the random slope are normally distributed. Shapiro tests concluded that the standardized EB of the random intercept are not significantly non-normal (p value= .337), however, the standardized EB of the random slope are significantly non-normal (p value= .00148). A multivariate normality test of the random intercept and the random slope, Mardia’s test, suggested that there is evidence of non-multivariate skewness (Statistic= 11.762, p value= .019), but there is evidence of multivariate kurtosis (Statistic= 1.782, p value= .075). To conclude, a multivariate normality is assumed because the deviations are not large enough. After selecting Model 3 with the level-1 and level-2 fixed and random effects of parentHED, variants of Model 3 were tested with additional level-1 and level-2 fixed effects of the other variables in the data to determine which fixed effects were significant when added to the model in Step 5.

Step 5. Model selection regarding fixed and random effects

Level-1 fixed and random effects

Each of the fixed effects of the five additional level-1 variables (cluster-mean-centered SES, cluster-mean-centered homework, cluster-mean-centered white, cluster-mean-centered sex, and cluster-mean-centered race) was added to the model one at a time. If a fixed effect was significant (p value <.05), it would remain included in the model for the remainder of the model building procedure. For example, the fixed effect of cluster-mean-centered (level-1) SES was added to Model 3 (with the pre-existing fixed effects β₀, β₁, and β₂) to create Model 4a:

$$ \begin{array}{@{}rcl@{}} y_{ij} &=& \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + b_{1j}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + \beta_{2}x^{(2)}_{\cdot j} \\ &&+ \beta_{3}(SES^{(1)}_{ij} - SES^{(2)}_{\cdot j}) + \epsilon_{ij}, \end{array} $$

(26)

where β₃ is the fixed effect of cluster-mean-centered SES. If β₃ is significant (p value < .05), the fixed effect of cluster-mean-centered SES is kept in the model when testing the next fixed effect (cluster-mean-centered homework). However, if β₃ is nonsignificant, the fixed effect of cluster-mean-centered homework would be tested by adding it to Model 3 (because the fixed effect of cluster-mean-centered SES was not kept in the model). Of the five level-1 fixed effects tested, only the fixed effects of cluster-mean-centered homework (p value < .001) and cluster-mean-centered white (p value= .0172) were significant and added to the model. A summary of the models tested is presented in Table 8. Based on the results in Table 8, the final model regarding the additional level-1 fixed effects was Model 4c:

$$ \begin{array}{@{}rcl@{}} y_{ij} &=& \beta_{0} + b_{0j} + \beta_{1}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) + b_{1j}(x^{(1)}_{ij} - x^{(2)}_{\cdot j}) \\ &&+ \beta_{2}x^{(2)}_{\cdot j} +\beta_{3}(homework^{(1)}_{ij} - homework^{(2)}_{\cdot j}) + \end{array} $$

$$ ~~~~~~~~~~~~\beta_{4}(white^{(1)}_{ij} - white^{(2)}_{\cdot j}) + \epsilon_{ij}, $$

(27)

where β₃ is the fixed effect of cluster-mean-centered homework, and β₄ is the fixed effect of cluster-mean-centered white. The addition of the level-1 fixed effects of cluster-mean-centered homework and white lowered the median SIQR from 0.7013 in Model 3 to 0.627 in Model 4c.

Table 8 Model comparisons with additional level-1 fixed effects of math data

Level-2 fixed effects

A similar model-building procedure was used to test the fixed effects of the thirteen additional level-2 variables (public, ratio, percmin, sctype, cstr, scsize, urban, region, SES cluster means, homework cluster means, white cluster means, sex cluster means, and race cluster means), with each fixed effect (if significant) being added to Model 4c one at a time. None of the thirteen level-2 fixed effects tested were significant when added to the model, with the smallest p value observed being .0914 for region. A summary of the models tested is presented in Table 9. None of the additional level-2 covariates was significant. Based on the results in Table 9, the final model with the additional level-1 and level-2 fixed effects was Model 4c. The parameter estimates of Model 3 (without the fixed effects of homework and white) are compared to those of Model 4c to examine the impact of these added parameters on parameter estimates, shown in Table 10. The estimates and standard errors of the fixed and random effects that were in both Model 3 and Model 4c were similar between the two models. In addition, the residual SD decreased (from 8.507 in Model 3 to 8.031 in Model 4c), indicative of the additional variability in math scores being accounted for in Model 4c with the inclusion of the level-1 fixed effects of cluster-mean-centered homework and white. Based on these results, Model 4c was selected as the final model regarding all level-1 and level-2 fixed and random effects for all variables.

Table 9 Model comparisons with additional level-2 fixed effects of math data

Table 10 Parameter estimate comparisons between Model 3 and Model 4c of math data

Evaluation of the selected model

The residuals of Model 4c were examined to determine if Model 4c adequately predicted math scores with the included level-1 and level-2 fixed and random effects, and whether the residuals of Model 4c are randomly and normally distributed. A scatter plot of the conditional standardized residuals vs. fitted values based on Model 4c was generated (see Fig. 3 [Step 5 (b)]). The conditional standardized residuals of Model 4c had no noticeable systematic trend, as residuals were scattered uniformly around zero. The lack of a systematic trend in residuals is indicative of Model 4c adequately estimating math scores without omitting a critical fixed or random effect. A Bartels ratio test conducted on the conditional standardized residuals of Model 4c showed that residuals were not significantly nonrandom (T = − 1.0716, n = 500, p value= .1422). Histograms of the level-1 conditional standardized residuals, the level-2 standardized EB of the random intercept, and the level-2 standardized EB of the random slope for Model 4c were plotted to evaluate the normality of residuals (these plots are not shown in the paper). The level-1 conditional standardized residuals are clearly normally distributed, which was not contradicted by a Shapiro’s test with a p value of .707. The small number of level-2 units makes it difficult to visually determine if the level-2 standardized EB of the random intercept and of the random slope are normally distributed. Shapiro tests concluded that the standardized EB of the random intercept are not significantly non-normal (p value= .839), however, the standardized EB of the random slope are significantly non-normal (p value= .010). A multivariate normality test of the random intercept and the random slope, Mardia’s test, indicated that multivariate normality assumption is rejected because of skewness (Statistic= 11.973, p value= .018), but not because of kurtosis (Statistic= 0.979, p value= .332).

Answers to the research question

As mentioned earlier, the goals of analysis using the math data set was to predict math scores from parents’ highest level of education (parentHED). Estimates of Model 4c reported in Table 10 were interpreted to answer this research question. Controlling for the level-1 homework and white covariates, the effect of the level-1 parentHED ($x_{ij}^{(1)}-x_{.j}^{(2)}$) was 2.520 (SE= 0.464, p value < 1e − 04) and the effect of the level-2 parentHED ($x_{.j}^{(2)}$) was 4.549 (SE= 0.647, p value < 1e − 04).

Example 2: Two-level longitudinal data (HD data)

Table 11 presents a summary of analyses and results.

Table 11 Summary of analyses and results for HD data

Step 0. A preliminary descriptive analysis

The primary research interest is the relationship between depression (measured with the HD rating scale) and the effect of a drug over time (using the Week variable for time). To begin, the HD rating was plotted over time (with 6 measurements taken over 5 weeks) for each of the two groups (Endog = 0, left, and Endog = 1, right, based on whether or not the depression was endogenous). Figure 4 (Step 0 (a)) shows a clear negative trend in HD rating over time for both groups. The overlapping red (linear trend) and blue (smooth curve) lines in the plots indicate that the negative trend in HD rating was linear.

Fig. 4

Diagnostic plots for random effects selection in the two-level longitudinal data (HD data)

Step 1. Random intercepts for the clusters

In this step, HD rating (y_ij) was modeled without any covariates. The first null model (Null Model Fixed) includes only a fixed intercept:

$$ y_{ij} = \beta_{0} + \epsilon_{ij}, $$

(28)

where y_ij is the HD rating for person j at time i, β₀ is the fixed intercept parameter, and 𝜖_ij is the random error¹⁰. The second null model (Null Model Random) includes only a random intercept:

$$ y_{ij} = \beta_{0} + b_{0j} + \epsilon_{ij}, $$

(29)

where b_0j is the random intercept parameter. The random errors for Null Model Fixed and Null Model Random (𝜖_ij) are assumed to be distributed as N(0,σ²R_j), with R_j = Λ_jC_jΛ_j for ${\Lambda }_{j} = I_{n_{j}}$ (with homoscedasticity) and $C_{j} = I_{n_{j}}$ (with uncorrelated errors), where n_j is the number of observations for person j (1 ≤ n_j ≤ 6).

To examine the multilevel nature of the data (with 6 measurements nested within persons), the standardized errors for Null Model Fixed and the conditional standardized errors for Null Model Random were plotted. For Null Model Fixed, standardized errors varied across persons, as shown in Fig. 4 (Step 1 (a)). The variability in standardized errors across persons in Fig. 4 (Step 1 (a)) is indicative of the multilevel nature of the data. Allowing the intercept to vary across persons in Null Model Random resulted in the conditional standardized errors, presented in Fig. 4 (Step 1 (b)). As shown in Fig. 4 (Step 1 (b)), conditional standardized errors for each person are distributed more consistently around 0 when the intercept is allowed to vary across persons. An ICC = .268 (meaning that 26.8% of the variance in HD scores is accounted for by the variability across persons) supports the conclusion that the data are multilevel, and the inclusion of a random intercept in the model is necessary.

Step 2. Fixed effect of level-1 covariate of interest

In this step the fixed effect of the level-1 covariate Week (the linear effect of the drug treatment on HD ratings over time) is added to Null Model Random to create Model 1:

$$ y_{ij} = \beta_{0} + \beta_{1}\texttt{Week}^{(1)}_{ij} + b_{0j} + \epsilon_{ij}, $$

(30)

where β₁ is the fixed effect of $\texttt {Week}^{(1)}_{ij}$, with $\texttt {Week}^{(1)}_{ij} = i$ being the number of weeks (0 ≤ i ≤ 5) since person j began the study.

Adding the fixed effect of the level-1 covariate Week decreased median SIQR from 0.487 in Null Model Random to 0.467 in Model 1 (indicating that Model 1 captured level-1 variability better than Null Model Random), and slightly decreased the SIQR(SIQR) from 0.178 in Null Model Random to 0.176 in Model 1 (indicating that Model 1 had highly comparable level-1 heteroscedasticity to Null Model Random).

Level-1 linearity

Week was plotted against the marginal standardized residuals of Model 1 to examine whether the relationship between Week and HD ratings was strictly linear. Figure 4 (Step 2 (a)) shows that there is a linear relationship (the mean of the marginal standardized residuals is approximately equal to zero) between Week and the marginal standardized residuals, indicating that there is no higher-order (e.g., square and/or cubic) relationship between Week and HD ratings. In addition, a smooth curve fitted to the marginal standardized residuals was not found to be significantly nonlinear (F = 0.027, edf = 1, p value= .941).

Level-1 heteroscedasticity

Fitted values of Model 1 were plotted against the conditional standardized residuals of Model 1 to explore the level-1 heteroscedasticity, as shown in Fig. 4 (Step 2 (b)). The conditional standardized residuals were not evenly distributed around 0 across the full range of fitted values, which is indicative of potential heteroscedasticity. This was further supported by a Levene’s test indicating that the conditional standardized residuals were significantly heteroscedastic (F = 2.666, df = 5, p value= .022).

Level-1 heteroscedasticity was included in the model to create Model 1a. The inclusion of level-1 heteroscedasticity changed the variance of the random residuals (𝜖_ij) from being fixed as ${\Lambda }_{j} = I_{n_{j}}$ (constant across time) in Model 1 to being estimable parameters (allowing variance to differ across time) in Model 1a. The fitted values of Model 1a were plotted against the conditional standardized residuals of Model 1a to investigate whether including level-1 heteroscedasticity had an impact (this plot is not shown in the paper). The conditional standardized residuals for Model 1a appear more evenly distributed around 0 than those of Model 1 (particularly for extreme fitted values). A Levene’s test indicated that the conditional standardized residuals were no longer significantly heteroscedastic (F = 0.262, df = 5, p value= .934). In addition, the SIQR(SIQR) decreased from 0.176 for Model 1 to 0.160 for Model 1a, indicating that Model 1a had less level-1 heteroscedasticity than Model 1. Based on these results, level-1 heteroscedasticity was assumed, and Model 1a was used instead of Model 1 for the remainder of the model-building process.

Correlated residuals

ARs of the marginal standardized residuals of Model 1a were plotted at each time lag to explore whether the residuals of Model 1a are correlated, as presented in Fig. 4 (Step 2 (c)). Solid lines in Fig. 4 (Step 2 (c)) represent the AR effects at each time lag, with dotted lines indicating the 99% confidence intervals centered at zero. There were significant AR effects at time lags 2-4 for Model 1a. Variations of Model 1a with different residual correlation structures (unstructured, compound, ARMA(1,0), ARMA(2,1), and ARMA(2,2)) were modeled in an attempt to reduce AR. However, results were unobtainable for Model 1a with the ARMA(2,1) and ARMA(2,2) correlation structures, due to the coefficient matrix being uninvertible (possibly due to overfitting). Autocorrelations of the conditional independent residuals for Model 1a with the unstructured, compound, and ARMA(1,0) correlation structures were plotted to examine the effectiveness of these correlation structures at reducing AR (these plots are not shown in the paper).¹¹ All three correlation structures resulted in decreased AR at each time lag, with all ARs falling within the 99% confidence intervals centered at zero. Although the compound correlation structure resulted in the smallest (or highly similar) AR at each time lag among the correlation structures examined, further analyses showed that the compound correlation structure resulted in a large number of level-1 outliers, with conditional independent residuals ranging from − 13.026 to 12.576. Although none of these level-1 outliers were influential enough to merit removal from the model, they resulted in significant violations of level-1 normality. For these reasons, the ARMA(1,0) correlation structure (which had generally lower AR in the residuals than the unstructured correlation structure) was selected instead.¹² Note that all AR with the ARMA(1,0) correlation structure were non-significant at the .01 confidence level, and the level-1 outliers and level-1 normality are less problematic with the ARMA(1,0) correlation structure than with the compound correlation structure, as discussed below. The version of Model 1a with the ARMA(1,0) correlation structure, referred to as Model 1b, was used for the remainder of the model-building process.

For the rest of the model-building process, conditional independent residuals of the fitted models are used for analyses instead of marginal standardized residuals, because errors are now allowed to correlate with the inclusion of the ARMA(1,0) structure in Model 1b.

Level-2 outliers

To detect level-2 outliers, a normal Q-Q plot of the standardized EB of the intercept for Model 1b was plotted against a theoretical normal distribution, presented in Fig. 4 (Step 2 (d)). The standardized EB of the intercept were largely normal, with several standardized EB falling slightly outside the 95% confidence bands. The standardized EB of the intercept for all level-2 units ranged from -0.864 to 1.098. Based on these results, no level-2 units were considered to be outliers.

Level-2 influential points

There were 13 level-2 influential points, having Cook’s distances exceeding the cutoff of 0.0606 = 4/66 for a sample size of 66 persons (see Fig. 4 [Step 2 (e)]). The Cook’s distances of these influential points ranged from 0.0857 to 0.242. However, none of these influential level-2 units were considered to be outliers (as these level-2 units had standardized EB of the intercept ranging from − 0.709 to 0.0246). Because these influential points are not expected to influence parameters in a way that disagreed with the rest of the data, removing these level-2 units from the data is not necessary.

Level-1 outliers

The fitted values from Model 1b were plotted against conditional independent residuals to detect level-1 outliers. As shown in Fig. 4 (Step 2(f)), there were 6 level-1 units detected with high conditional independent residuals, ranging in magnitude from 2.362 to 3.649.

Level-1 influential points

No level-1 influential points were detected as having a Cook’s distance greater than the cut-off of 1. The highest Cook’s distance observed was 0.147, as presented in Fig. 4 (Step 2 (g)). Because no level-1 unit (including those with large conditional independent residuals) was expected to influence parameter estimates, all level-1 units were considered acceptable to remain in the data. If any of the outlying level-1 units had been found to be influential as well, they would be marked for removal from the data in Step 4 (if they were found to be influential outliers in Step 4 as well).

Level-1 normality

A normal Q-Q plot was generated to examine whether the conditional independent residuals of Model 1b were normally distributed (see Fig. 4 [Step 2 (h)]). Conditional independent residuals appeared somewhat non-normal in the extremes. In addition, a Shapiro–Wilk test indicated that the conditional independent residuals were significantly non-normal (W = 0.989, p value= .005). A histogram of the conditional independent residuals was overlaid with a normal curve to further examine normality (this plot is not shown in the paper). The histogram showed that the deviance from normality is not large. Therefore, level-1 normality was assumed for Model 1b based on this analysis.

Level-2 normality

A normal Q-Q plot was generated to examine whether the standardized EB of the intercept of Model 1b were normally distributed (see Fig. 4 [Step 2 (i)]). The resulting Q-Q plot shows that the standardized EB of the intercept are mostly normal for Model 1b, with a few standardized EB falling slightly outside the 95% confidence bands. A histogram of the standardized EB of the intercept was plotted to further examine level-2 normality (this plot is not shown in the paper). The standardized EB of the intercept showed no drastic deviations from normality (such as outlying clusters with large standardized EB). Based on these results, level-2 normality was assumed for Model 1b.

Step 3. Random effects of the level-1 covariate

In this step the random effect of the level-1 covariate Week was added to Model 1b, creating Model 2:

$$ y_{ij} = \beta_{0} + b_{0j} + \beta_{1}\texttt{Week}^{(1)}_{ij} + b_{1j}\texttt{Week}^{(1)}_{ij} + \epsilon_{ij}, $$

(31)

where b_1j is the random slope of $\texttt {Week}^{(1)}_{ij}$. Note that Model 2 still includes the random effect for level-1 heteroscedasticity and the ARMA(1,0) correlation structure.

Adding the random effect of the level-1 covariate Week increased the SIQR(SIQR) from 0.117 in Model 1b to 0.174 in Model 2 (indicating that Model 2 had more level-1 heteroscedasticity than Model 1b). To explore this increase in SIQR(SIQR), boxplots of the SIQR for persons were plotted for Model 1b and Model 2, as shown in Fig. 4 (Step 3 (a)). The inclusion of the random effect of the level-1 covariate in Model 2 resulted in a few extreme outlying SIQR, causing the interquartile range of SIQR to “expand” at the upper end to include previously outlying SIQR. This “expansion” resulted in an increase in the SIQR(SIQR) of Model 2.

The ordinary least squares (OLS) regression lines predicting HD rating with Week for each person were plotted to show the variability in the effect of Week across persons, as presented in Fig. 4 (Step 3 (b)). Variability in the intercepts across persons is indicative of the need for the random effect of the intercept (b_0j), whereas variability in the slopes across persons is indicative of the need for the random effect of the slope (b_1j).

Plots for level-1 and level-2 outliers, influential points, and normality are not presented to save space. The plots are similar to the plots shown in Fig. 4 (Step 2 (d) - (i)).

Level-2 outliers

To detect level-2 outliers, a normal Q-Q plot of the standardized EB of the intercept for Model 2 was plotted against a theoretical normal distribution. No level-2 units (persons) were detected as outliers, with all standardized EB of the intercept falling within the 95% confidence bands. In addition, none of these level-2 units were found to be outliers in a box plot of the standardized EB of the intercept. The standardized EB of the intercept for all level-2 units ranged from -1.330 to 2.145. Based on these results, no level-2 units were considered to be outliers.

Level-2 influential points

There were three level-2 influential points, having Cook’s distances of 0.0635, 0.0779, and 0.114, exceeding the cutoff of 0.0606 = 4/66 for a sample size of 66 persons. None of these level-2 influential points were considered to be outliers (having standardized EB of the intercept of 0.574, 1.373, and − 0.770, respectively). Because none of these influential points were outliers, their removal from the data was not necessary.

Level-1 outliers

The fitted values from Model 2 were plotted against the conditional independent residuals to detect level-1 outliers. There were 10 level-1 outliers detected, with conditional independent residuals ranging in magnitude from 2.116 to 3.893. They will be investigated on how influential they are.

Level-1 influential points

No level-1 influential points were detected, as no point had a Cook’s distance larger than the cut-off of 1. The largest Cook’s distance observed was 0.027. Because no level-1 unit (including those with large conditional independent residuals) is expected to influence parameter estimates, all level-1 units were considered acceptable to remain in the data.

Level-1 normality

A normal Q-Q plot was generated to examine whether conditional independent residuals of Model 2 were normally distributed. Conditional independent residuals appeared somewhat non-normal in the extremes, with several residuals falling outside the 95% confidence bands. To further examine level-1 normality, a histogram of the conditional independent residuals of Model 2 was overlaid with a normal curve. The Q-Q plot and histogram of the conditional independent residuals of Model 2 were highly similar to those for Model 1b, with no extreme violations of level-1 normality detected. As a result, level-1 normality was assumed for Model 2.

Level-2 normality

Normal Q-Q plots were generated to examine whether the standardized EB of the intercept and of the slope of Model 2 were normally distributed. The resulting Q-Q plots show that the standardized EB of the intercept and of the slope are mostly normal for Model 2, with only a few standardized EB of the slope falling slightly outside the 95% confidence bands. Histograms of the standardized EB of the intercept and of the slope were plotted to further examine level-2 normality. The histograms of standardized EB of the intercept and of the slope showed no drastic deviations from normality (such as outlying clusters with large standardized EB). Based on these results, level-2 normality was assumed for Model 2.

A Mardia’s test was conducted to evaluate the multivariate normality of the standardized EB of the intercept and of the slope of Model 2. The assumptions of multivariate non-skewness (Statistic = 7.815, p = .0986) and multivariate non-kurtosis (Statistic = − 0.545, p value= .586) were not significantly violated at the .05 significance level. Based on these results, level-2 multivariate normality was assumed for Model 2.

Step 4. Fixed Effects of the Level-2 Covariate

In this step the fixed effect of the level-2 covariate Endog was added to Model 2, creating Model 3:

$$ y_{ij} = \beta_{0} + b_{0j} + \beta_{1}\texttt{Week}^{(1)}_{ij} + \beta_{2}\texttt{Endog}^{(2)}_{j} + b_{1j}\texttt{Week}^{(1)}_{ij} + \epsilon_{ij}, $$

(32)

where β₂ is the fixed effect of the $\texttt {Endog}^{(2)}_{j}$ level-2 covariate. $\texttt {Endog}^{(2)}_{j} = 1$ if person j’s depression is endogenous, and $\texttt { Endog}^{(2)}_{j} = 0$ otherwise. Model 3 still includes the random effect for level-1 heteroscedasticity and the ARMA(1,0) correlation structure.

Potential inclusion of the level-2 covariate

To explore whether Endog should be included in the model, the standardized EB of the random slope for Model 2 (Equation 31, which does not include the level-2 covariate) was plotted for each value of Endog, as presented in Fig. 4 (Step 4 (a)). The histogram (overlaid with scatter plots of the standardized EB for group) shows that the mean standardized EB of the random slope for Model 2 was -0.077 when Endog = 0, and 0.060 when Endog = 1, illustrating the variability in HD ratings unaccounted for by omitting Endog in Model 2. The difference between these two groups was not very large (with a mean difference of 0.137). The standardized EB of the random slope for Model 3 (with Endog included in the model) was plotted for comparison, as shown in Fig. 4 (Step 4 (b)). With the inclusion of Endog in Model 3, the mean standardized EB of the random slope was highly similar between the two values of Endog (− 0.016 when Endog = 0 and 0.012 when Endog = 1). The above histograms show that the standardized EB of the random slope were highly similar between Model 2 and Model 3.

The addition of the fixed effect of the level-2 covariate slightly increased the SIQR(SIQR) from 0.1741 in Model 2 to 0.1744 in Model 3. These highly similar SIQR(SIQR) (with the difference between the two models being < 0.0004) indicate that Model 2 and Model 3 have similar levels of level-1 heteroscedasticity. To further illustrate the similarity in SIQR(SIQR) between these two models, boxplots of the SIQR for persons were plotted for Model 2 and Model 3. Figure 4 (Step 4 (c)) shows that the interquartile range of the SIQR (and by extension the SIQR(SIQR)) are highly similar between Model 2 and Model 3.

Based on these analyses, the level-2 covariate Endog was not considered necessary to include in the model. Model 2 was used instead of Model 3 for the remainder of the model building process. Because Model 2 was selected, the analyses for outliers, influential points, and non-normality in this step are identical to the analyses presented in Step 3.

Outlier removal

If any level-1 and/or level-2 units were found to be both outlying and influential in this step, they would be removed from the data and Steps 1–4 would be repeated. However, because no outlying and influential level-1 and/or level-2 units were detected for Model 2 in Step 3, such outlier removal was not necessary for this illustration.

Step 5. Model selection regarding fixed and random effects

In this step, the models analyzed in Steps 1–4 are compared regarding differences between their predicted values and the observed data. In Table 12, the diagnostic measures (RMSE, Median SIQR, and SIQR(SIQR)) for the summary of results and model selection methods (AIC and BIC) are reported.¹³

Table 12 Model comparisons regarding diagnostic measures of HD data

As discussed in Step 4, Models 2 and 3 were highly similar, with the inclusion of the Endog variable not found to be necessary. The added model complexity of Model 3 was evaluated by AIC and BIC, with AIC indicating the fixed effect of Endog worth including in the model (despite the added complexity), and BIC (which punishes model complexity more harshly than AIC) indicating that this parameter was not worth including in the model (with Model 2 having a lower BIC than Model 3).

As investigated in Step 3, Models 2 and 3 (which both include the random effect of the level-1 Week covariate) had several outlying SIQR for persons, which caused the interquartile range of SIQR across persons (and thus the SIQR(SIQR)) to “expand.” As a result, Model 1b (which does not include the random effect of the level-1 covariate, and therefore does not have these outlying SIQR) had the smallest median SIQR and SIQR(SIQR) of the four models. Model 2 had a slightly lower median SIQR and SIQR(SIQR) than Model 3, however, the boxplots of SIQR for persons presented in Step 4 were highly similar between Models 2 and 3. This result indicates that the degrees of variability and heteroscedasticity accounted by Models 2 and 3 are similar.

Taking all results together, Model 2 was selected as the best-fitting model, with level-1 fixed and random effects of Week, level-1 heteroscedasticity, and an ARMA(1,0) correlation structure. The added value of the Endog variable was not considered significant important to select Model 3. The parameter estimates of the selected model (Model 2) are presented in Table 13.

Table 13 Parameter estimates of Model 2 of HD data

Evaluation of the selected model

The residuals of Model 2 were examined to determine if Model 2 adequately explained HD rating, with Week, level-1 heteroscedasticity, and the ARMA(1,0) correlation structure, and whether the conditional independent residuals of Model 2 are randomly and normally distributed. A scatter plot of the conditional independent residuals vs. fitted values of Model 2 was generated, as shown in Fig. 4 (Step 5 (a)). The conditional independent residuals of Model 2 had no noticeable systematic pattern, with residuals being scattered uniformly around zero. The lack of a systematic pattern in the residuals is indicative of Model 2 adequately explaining HD rating without omitting a critical fixed or random effect (such as the level-2 fixed effect of Endog). A Bartels ratio test conducted on the conditional standardized residuals of Model 2 showed that residuals were not significantly nonrandom (T = 4.253, n = 375, p value ≈ 1). In addition, based on a Durbin-Watson test conducted on the conditional standardized residuals of Model 2, it was concluded that the first-order AR was not statistically significantly (DW = 2.453, p value ≈ 1).

Histograms of the level-1 conditional independent residuals, the level-2 standardized EB of the random intercept, and the level-2 standardized EB of the random slope for Model 2 were plotted to evaluate the normality of residuals (these plots were not shown in the paper). As discussed in Step 3, level-1 normality in the conditional independent residuals and level-2 normality in the standardized EB of the intercept and of the slope were assumed for Model 2. In addition, the standardized EB of the intercept and of the slope of Model 2 were shown in Step 4 to be multivariate normally distributed.

Answers to the research question

Results of the selected model (Model 2) are presented in Table 13. The weeks covariate was coded as 0, 1, 2, 3, 4, and 5. Given this coding, the intercept estimate (23.509, SE= 0.533) indicates that patients start with an HD score of 23.509 on average. There was nonignorable variability around the average scores across patients (V ar(b_0j) = 3.248²). The average weekly linear change in HD scores for patients with average drug levels was − 2.384 (SE= 0.210), indicative of a decrease in the degree of depression over time per week. There was variability in the linear change in HD scores across patients (V ar(b_1j) = 1.364²) and there was no clear support for an effect of endogeneity of the depression.

Summary and discussion

Residual-based diagnostic plots and measures have been extensively used in single-level linear regression models. However, such plots and measures are rather unusual in model selection and model checking in MLM applications. In this paper, we listed types of random effects presented in MLMs for two-level cross-sectional and longitudinal data, and provided a generic description of these random effects to guide researchers towards selecting the necessary random effects. In addition, we reviewed level-specific diagnostic plots using various kinds of level-specific residuals to select a random effect and to check model assumptions. Furthermore, we presented statistical tests and diagnostic measures to interpret patterns in the diagnostic plots. Using two empirical data sets, the existing and proposed methods were illustrated to demonstrate how to select necessary fixed and random effects in model-building steps. R code is provided for all analyses conducted in these illustrations.

Guidelines for the use of diagnostic measures, plots, and tests in model-building steps

For the longitudinal and cross-sectional illustrations, only one or two iterations (respectively) of the analyses described were required to select a model to answer research questions. However, longer iterative processes may be necessary in practice. For example, in Step 5 (model selection regarding fixed and random effects), large discrepancies may be found between data and fitted values for a selected model. If the discrepancies stem from data characteristics missed in the earlier steps (e.g., some individuals have different slopes), one can return to Step 3 (random effects of the level-1 covariates) and/or Step 4 (fixed and random effects of the level-2 covariate). Not only do we recommend going through the model-building steps to obtain the best-fitting model to the data, but it may be necessary to use multiple iterations because earlier decisions may look sub-optimal at later steps. An optimal set of fixed and random effects is crucial for ‘correct’ statistical inferences regarding an effect of interest.

In the illustrative data sets, there is one covariate of interest for which Steps 2–4 were conducted (confirmatory hypothesis testing) and additional covariate(s) (functioning as control covariates) for which Step 5 was conducted (an exploratory approach). When there are multiple covariates of interest from research questions, we suggest conducting Step 2 and Step 3 for each of the level-1 covariates of interest and Step 4 for each of the level-2 covariates of interest. When there are multiple covariates of interest, the model complexity regarding random effects can dramatically increase. In the present study, a model is built by starting with a null model and then slowly adding fixed and random effects based on the diagnostic measures, plots, and statistical tests as described. As illustrated, the use of diagnostic measures, plots, and tests can be useful to have a parsimonious model that provides an adequate description of the data. The model-building steps starting with a null model tend to keep the models simple (Hox et al., 2018, p. 43).

The model-building steps in the two applications are exploratory in nature, so that in Step 5 hypotheses can be tested regarding covariate(s) of interest. It is possible that decisions leading to the selected model are based on sample variation. When the sample size is large enough, we recommend cross-validation of the selected model (see Camstra & Boomsma, 1992, for review). As an example, Hox et al., (2018) suggested using one half of the data to build up models and using the other half for cross-validation of the selected model.

We use diagnostic measures, plots, and tests for residuals as a supplement to common model selection methods (e.g., AIC and BIC) or significance tests (e.g., Wald test). As presented in the illustrations, we recommend using diagnostic measures, plots, and tests for residuals even when the common model selection methods and significance testing of effects suggest a certain model. For example, in the illustration of the cross-sectional data set, the nonlinearity of the level-2 covariate was observed in a diagnostic plot (a plot of the standardized EB of the random slope vs. the level-2 covariate) in the first iteration (prior to deleting the single level-2 outlier), and based on AIC, BIC, and significance tests of higher-order terms of the covariate. However, we found that the nonlinearity is caused by a single level-2 outlier, based on (a) further analyses of diagnostic plots and measures (plot comparisons of the standardized EB of the random slope vs. the level-2 covariate and RMSE comparisons for models with and without the higher-order terms of the covariates), and (b) analyses of level-specific outliers and influential points in the suggested model-building steps. Based on these results, a model with the linearity of the level-2 covariate (without the single level-2 outlier) was selected.

In the illustrative cross-sectional data set, the single level-2 outlier was detected and removed. When a large number of of outliers are detected, researchers can use robust estimation methods such as the rank based and heavy tailed methods (e.g., Finch, 2017 for comparisons) and robust S-estimation (Copt and Victoria-Feser, 2006) to avoid removing large quantities of the data. We also suggest looking into Demidenko (2004, Section 4.4) for alternative approaches to robust modeling.

As far as normality is concerned, extreme non-normality was not encountered in either of the illustrations, neither of level-1 residuals, nor of EB estimates of random effects. Maas and Hox (2004) found via simulation studies that the non-normality of the level-1 residuals in MLM does not affect the estimates and standard errors of fixed effects, but non-normality does result in biased standard errors of variances of random effects. In addition, Maas and Hox (2004) reported that robust standard errors do not solve the non-normality of the level-1 residuals when the residuals are largely skewed. When there is an extreme deviation from normality in the level-1 residuals, a nonparametric estimate of the bivariate density of the random intercept and slope can be considered using a penalized Gaussian mixture linear mixed model (e.g., Ghidey, Lesaffre, & Eilers, 2004).

Limitations of the present study

This study provides initial guidance to researchers to build up MLMs using diagnostic measures, plots, and tests for 2-level nested data. In applying MLMs for multilevel data having more than 2 nested levels, additional EB of random effects at the 3rd level or higher can be obtained, along with the level-1 residuals and level-2 random effects we described in the current study. Similar diagnostic measures, plots, and tests to those presented for the level-2 data are applicable to multilevel data with more than 2 levels. However, we expect that model-building strategies can be more complex for such data, especially when multiple iterations are desirable (i.e., returning to earlier steps). Future research applying these methods to higher-level data could be useful.

Illustrations of the present study are restricted to a case when there is a single covariate of interest based on a research question and in the presence of control covariates. Although the guidelines of model building for multiple covariates of interest are briefly discussed, step-by-step illustrations are needed in future research. In addition, additional diagnostic plots and tests are needed to explore additional complexities we did not illustrate in the present study. For example, when there are multiple level-1 covariates of interest, a plot of OLS regression coefficients per cluster for the level-1 covariates can be further considered in Step 3.

For the detection of the level-specific influential points, specific detection methods and their cut-off values were used in this study, as used in the MLM literature. To the best of our knowledge, there is no consensus regarding the “correct” detection method of the level-specific influential points and their specific cutoffs to use in MLM. Systematic comparisons of various detection methods are required in future studies. Furthermore, for the detection of the level-specific outliers, the univariate detection method was used for computational efficiency and the use of robust estimation methods was recommended when there are many outliers. However, without further studies on the level-specific outliers, it would be difficult to create an absolute guideline on when to use the univariate method instead of the multivariate detection method and on when to use the robust estimation methods that would be applied in the same way to all MLM applications.

This study uses a single software package (the nlme package in R), to fit MLMs and to calculate level-specific residuals. There are other software packages which provide different kinds of residuals and diagnostic measures, as reviewed by O’Connell et al., (2016) (see Table 4.1) and Loy and Hofmann (2014) (see Table 1). Currently, there are no other software packages which provide the functions required to perform all of the procedures we presented in this paper. Future research is required to provide guidelines on how to replicate the model-building and analyses conducted in this study using other software packages than nlme.

Despite these limitations, our work clearly underscores the benefits of using diagnostic measures, plots, and tests in the applications of MLMs. We hope to encourage researchers to explore and visualize data in model selection and model checking in their applications of MLMs.