Abstract
We formally introduce a novel, yet ubiquitous, category of norms: norms of instrumentality. Norms of this category describe which actions are obligatory, or prohibited, as instruments for certain purposes. We propose the Logic of Agency and Norms (\(\mathsf {LAN}\)) that enables reasoning about actions, instrumentality, and normative principles in a multi-agent setting. Leveraging \(\mathsf {LAN}\), we formalize norms of instrumentality and compare them to two prevalent norm categories: norms to be and norms to do. Last, we pose principles relating the three categories and evaluate their validity vis-à-vis notions of deliberative acting. On a technical note, the logic will be shown decidable via the finite model property.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Notice that principle P2 incorporates a form of defeasible reasoning through explicit exception, for the present analysis of norms of instrumentality, the above will suffice.
- 2.
Notice that in the present example, we use a material tool to exemplify instruments. However, we stress that the notion of instrumentality is more general and refers to all actions serving goals; e.g. ‘opening the window’ is an instrument for ‘changing the room’s temperature’ [22]. Following Von Wright [23], an action is a classified \(\phi \)-instrument—where \(\phi \) is the purpose—whenever the action serves the purpose of \(\phi \). Consequently, although in the above example reference is made to a ‘scalpel’ (i.e. a tool) the instrument under consideration—serving the purpose of ‘the incision being made’—is in fact the action ‘using the scalpel (for the purpose of incision)’. See [4] for a philosophical discussion on different notions of instrumentality.
- 3.
Following [1], to avoid paradoxes \(\mathfrak {v}^{\alpha _i}\) is read as ‘norm violation’ instead of ‘sanction’.
- 4.
We note in passing that one could define other action operators of \(\mathsf {PDL}\) within the reduced logic \(\mathsf {LAN}\); for example ‘composition’ as \([\varDelta ^{\alpha _i} ; \varGamma ^{\alpha _i}]\phi := [\varDelta ^{\alpha _i}][\varGamma ^{\alpha _i}]\phi \).
- 5.
Notice, since \(Act_{\mathsf {LAN}}\) represents a Boolean algebra of actions built over a finite number of actions types from Act, there are only finitely many equivalence classes \([\![ \varDelta ^{\alpha _i} ]\!]~:=~\{\varGamma ^{\alpha _i} \ | \ \vdash _{\mathsf {LAN}} t(\varGamma ^{\alpha _i}) \equiv t(\varDelta ^{\alpha _i}) \}\) of equivalent actions. We let \([\![ Act^{*}_{\mathsf {LAN}} ]\!]\) in F1\(^\prime \) and O1\(^\prime \) represent the set of all such equivalence classes minus the class \([\![ \bot ^{\alpha _i} ]\!]\) of all impossible actions. Additionally, since obligatory or forbidden results are central to norms to be, as opposed to obligatory or forbidden actions, we impose the following restriction on F1, O1, F1\(^\prime \) and O1\(^\prime \): the formula \(\phi \) is free of action constants from Wit. Without this restriction, norms to do could be seen as instances of norms to be—i.e. norms to bring about the witness of a performed action as a result—thus contradicting the observations made in [1] about the irreducibility of the two.
- 6.
The assumption avoids risk by forbidding acts that possibly produce violations; e.g. ‘it is forbidden to injure someone with a sharp tool, independent of the ability to guarantee the injury’. However, one could consider inclusion of instrumentality clauses for prohibitions when analyzing responsibility. We leave this for future work.
References
d’Altan, P., Meyer, J.J., Wieringa, R.J.: An integrated framework for ought-to-be and ought-to-do constraints. Artif. Intell. Law 4(2), 77–111 (1996)
Anderson, A.R., Moore, O.K.: The formal analysis of normative concepts. Am. Sociol. Rev. 22(1), 9–17 (1957)
Belnap, N., Perloff, M., Xu, M.: Facing the Future. Agents and Choices in our Indeterminist World. Oxford University Press, Oxford (2001)
van Berkel, K., Pascucci, M.: Notions of instrumentality in agency logic. In: Miller, T., Oren, N., Sakurai, Y., Noda, I., Savarimuthu, B.T.R., Cao Son, T. (eds.) PRIMA 2018. LNCS (LNAI), vol. 11224, pp. 403–419. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03098-8_25
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Broersen, J.: Deontic epistemic stit logic distinguishing modes of mens rea. J. Appl. Logic 9(2), 137–152 (2011)
Brown, M.A.: On the logic of ability. J. Philos. Logic 17(1), 1–26 (1988)
Castañeda, H.N.: On the semantics of the ought-to-do. In: Davidson, D., Harman, G. (eds.) Semantics of Natural Language. Synthese Library, vol. 40, pp. 675–694. Springer, Dordrecht (1972). https://doi.org/10.1007/978-94-010-2557-7_21
Chisholm, R.: Contrary-to-duty imperatives and deontic logic. Analysis 24, 33–36 (1963)
Fischer, M., Ladner, R.: Propositional dynamic logic of regular programs. J. Comput. Syst. Sci. 18(2), 194–211 (1979)
Governatori, G.: Practical normative reasoning with defeasible deontic logic. In: d’Amato, C., Theobald, M. (eds.) Reasoning Web 2018. LNCS, vol. 11078, pp. 1–25. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00338-8_1
Governatori, G., Hashmi, M.: No time for compliance. In: 19th International Enterprise Distributed Object Computing Conference, pp. 9–18. IEEE (2015)
Governatori, G., Olivieri, F., Rotolo, A., Scannapieco, S.: Computing strong and weak permissions in defeasible logic. J. Philos. Logic 42(6), 799–829 (2013). https://doi.org/10.1007/s10992-013-9295-1
Hansson, S.O.: The varieties of permission. In: Gabbay, D., Horty, J., Parent, X., van der Meyden, R., van der Torre, L. (eds.) Handbook of Deontic Logic and Normative Systems, pp. 195–240. College Publications, London (2013)
Horty, J.: Agency and Deontic Logic. Oxford University Press, Oxford (2001)
Kant, I.: Critique of Pure Reason. Cambridge University Press, Cambridge (2000)
Meyer, J.J.C.: A different approach to deontic logic: deontic logic viewed as a variant of dynamic logic. Notre Dame J. Formal Logic 29(1), 109–136 (1988)
Pascucci, M.: Anderson’s restriction of deontic modalities to contingent propositions. Theoria 83(4), 440–470 (2017)
Prakken, H., Sergot, M.: Dyadic deontic logic and contrary-to-duty obligations. In: Nute, D. (ed.) Defeasible Deontic Logic, pp. 223–262. Springer, Dordrecht (1997). https://doi.org/10.1007/978-94-015-8851-5_10
Prisacariu, C., Schneider, G.: A dynamic deontic logic for complex contracts. J. Logic Algebraic Program. 81(4), 458–490 (2012)
von Wright, G.H.: Deontic logic. Mind 60(237), 1–15 (1951)
von Wright, G.H.: An Essay in Deontic Logic and the General Theory of Action. North Holland Publishing Company, Amsterdam (1968)
von Wright, G.H.: The Varieties of Goodness. Routledge & Kegan Paul, London and Henley (1972). fourth impression
Acknowledgments
Work funded by projects: FWF I2982, FWF W1255-N23, FWF Y544-N2, and WWTF MA16-028.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Finite Model Property and Decidability
A Finite Model Property and Decidability
In this appendix, we provide the main technical contribution of this paper: we show that \(\mathsf {LAN}\) is decidable (Corollary 1), via proving the finite model property (FMP) for the logic (Theorem 2). Our strategy is, accordingly: first, we show that every satisfiable formula is satisfiable on a treelike model (Lemma 1). Second, we show that the depth of the treelike model can be bounded (Lemma 2). Last, we prove that the breadth of the model can be bounded (Lemma 3).
Lemma 1
Every formula \(\phi \in \mathcal {L}_{\mathsf {LAN}}\) satisfiable on a \(\mathsf {LAN}\)-model, is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model.
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a \(\mathsf {LAN}\)-model with \(w \in W\) and assume \(M, w \models \phi \) (i.e. \(\phi \) is satisfiable). To show that \(\phi \) is satisfiable at the root of a treelike model we evoke an unraveling procedure similar to the one in [5, Ch. 2.1]. We define the treelike model \(M^t\) as follows:
-
\(W^t \subseteq \bigcup _{n \in \mathbb {N}} W^{n}\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(wRw_{1}\), \( w_{1}Rw_{2}\), ..., \(w_{n-1}Rw_{n}\);
-
For each \(\alpha _{i} \in Agt\) and each \(\mathfrak {d}^{\alpha _{i}}_{j} \in Wit^{\alpha _{i}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^t \subseteq W^t\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(w_{n} \in W_{\mathfrak {d}^{\alpha _{i}}_{j}}\);
-
For each \(\alpha _{i} \in Agt\), \(W_{\mathfrak {v}^{\alpha _i}}^t \subseteq W^t\) is the set of all finite sequences \((w,w_{1},{...},w_{n})\) s.t. \(w_{n} \in W_{\mathfrak {v}^{\alpha _i}}\);
-
For all \(\varvec{w}, \varvec{u} \in W^t\), \(\varvec{w}R^t\varvec{u}\) iff \(\varvec{w} = (w,w_{1},{...},w_{n})\), \(\varvec{u} = (w,w_{1}{...},w_{n},w_{n+1})\), and \(w_{n}Rw_{n+1}\);
-
For all \(\varvec{w}, \varvec{u} \in W^t\), \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\) iff \(\varvec{w} = (w,w_{1},{...},w_{n})\), \(\varvec{u} = (w,w_{1}{...},w_{n},w_{n+1})\), and \(w_{n}R_{\mathsf {N}}w_{n+1}\);
-
For all \(\varvec{w} \in W^t\), \(\varvec{w} = (w,w_{1},{...},w_{n}) \in V^t(p)\) iff \(w_{n} \in V(p)\).
The model \(M^t\) is clearly treelike. Further, Prop. 2.14 and 2.15 of [5] imply:
-
(1)
For any formula \(\psi \in \mathcal {L}_{\mathsf {LAN}}\), each \(u \in W\), and each \(\varvec{u} \in W^t\) of the form
$$\begin{aligned} (w, w_{1}, {...}, u), \text { we have that } M,u \models \psi \text { iff } M^t,\varvec{u} \models \psi . \end{aligned}$$
This result, together with the assumption \(M, w \models \phi \), implies \(M^t, (w) \models \phi \), where (w) is the root of the treelike model \(M^t\). To complete the proof, we must argue that \(M^t\) is a \(\mathsf {LAN}\)-model, i.e., it satisfies conditions (R3)–(R6) of Definition 5:
(R3) Let \(\varvec{w}, \varvec{u}, \varvec{v} \in W^t\) and suppose \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\) and \(\varvec{w}R_{\mathsf {N}}^t\varvec{v}\). By definition of \(R_{\mathsf {N}}^t\) we get (i) \(\varvec{w}\) is a sequence of the form \((w,w_{1},{...},w_{n})\), (ii) \(\varvec{u}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1})\), (iii) \(\varvec{v}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1}')\), (iv) \(w_{n}R_{\mathsf {N}}w_{n+1}\), and (v) \(w_{n}R_{\mathsf {N}}w_{n+1}'\). Since the original model M satisfies (R3), it follows from (iv) and (v) that \(w_{n+1} = w_{n+1}'\), which, together with (ii) and (iii), implies \(\varvec{u} = \varvec{v}\).
(R4) Let \(\varvec{w}, \varvec{u} \in W^t\) and assume \(\varvec{w}R_{\mathsf {N}}^t\varvec{u}\). By definition of \(R_{\mathsf {N}}^t\) we get (i) \(\varvec{w}\) is a sequence of the form \((w,w_{1},{...},w_{n})\), (ii) \(\varvec{u}\) is a sequence \((w,w_{1},{...},w_{n},w_{n+1})\), and (iii) \(w_{n}R_{\mathsf {N}}w_{n+1}\). Since the original model M satisfies (R4), it follows from (iii) that \(w_{n}Rw_{n+1}\), which, together with (i) and (ii), implies \(\varvec{w}R^t\varvec{u}\).
(R5) Let \(\varvec{w} \in W^t\) and \(Agt = \{\alpha _{1}, ..., \alpha _{n}\}\). Suppose there are (not necessarily distinct) action-types \(\varDelta _{1}, {...}, \varDelta _{n} \in Act_{\mathsf {LAN}}\) s.t. for \(1 \le i \le n\) there exist \(\varvec{u}_{i} \in W^t\) s.t. \(\varvec{w}R^t\varvec{u}_{i}\) and \(\varvec{u}_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{t}\). It follows that \(\varvec{w}\) is of the form \((w,w_{1},{...},w_{n})\) and each \(\varvec{u}_{i}\) is of the form \((w,w_{1},{...},w_{n},u_{i})\) with \(w_{n}Ru_{i}\). The model M satisfies condition (R5), and hence there exists a world \(v \in W\) s.t. \(w_{n}Rv\) and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\). By definition of \(M^t\), we have \(\varvec{v} = (w,w_{1},{...},w_{n},v) \in W^t\), implying that \(\varvec{w}R^{t}\varvec{v}\) and \(\varvec{v} \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{t} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{t}\).
(R6) Let \(\varvec{w} \in W^t\) and \(\alpha _{i} \in Agt\). Assume there is a \(\varvec{v} \in W^t\) s.t. \(\varvec{w}R^t\varvec{v}\) and \(\varvec{v} \in W_{\mathfrak {v}^{\alpha _i}}^{t}\). This implies \(\varvec{w} = (w,w_{1},{...},w_{n})\) and \(\varvec{v} = (w,w_{1},{...},w_{n},v)\) with \(w_{n}Rv\). Since M satisfies (R6), there is a u s.t. \(w_{n}Ru\) and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\). By definition of \(M^t\), there is a \(\varvec{u} = (w,w_{1},{...},w_{n},u) \in W^t\) s.t. \(\varvec{w}R^t\varvec{u}\) and \(\varvec{u} \in W^{t} - W_{\mathfrak {v}^{\alpha _i}}^{t}\).
For the second transformation we define the following auxiliary concepts:
Definition 7
(Degree \(deg(\cdot )\)). The modal degree is recursively defined as:
-
\(deg(p) = deg(\mathfrak {d}^{\alpha _{i}}_{j}) = deg(\mathfrak {v}^{\alpha _i}) = 0\);
-
\(deg(\lnot \phi ) = \deg (\phi )\);
-
\(deg(\phi \rightarrow \psi ) = max\{\deg (\phi ),deg(\psi )\}\);
-
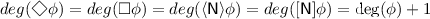 .
.
Definition 8
(Height \(height(\cdot )\) and Depth). Let M be a treelike model. We define the height of a node w in M recursively as follows:
-
\(height(w) = 0\), if w is the root of M;
-
\(height(w) = height(u) + 1\), if uRw in M.
The depth of M is the maximum height among all the worlds in M.
Lemma 2
Every formula \(\phi \) satisfiable at the root of a treelike \(\mathsf {LAN}\)-model, is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth (specifically, with a depth equal to \(deg(\phi )\)).
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a treelike \(\mathsf {LAN}\)-model with root \(w\in W\) and assume \(M, w \models \phi \). We first construct a treelike model \(M^d\) of finite depth by restricting the depth of \(M^d \) to \(deg(\phi )\) and argue that \(\phi \) is satisfiable at the root w of \(M^{d}\). We define \(M^d\) as follows:
-
For all \(w \in W\), \(w \in W^{d}\) iff \(height(w) \le deg(\phi )\);
-
For all \(\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^{d} = W_{\mathfrak {d}^{\alpha _{i}}_{j}} \cap W^{d}\);
-
For all \(\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {v}^{\alpha _i}}^{d} = W_{\mathfrak {v}^{\alpha _i}} \cap W^{d}\);
-
\(R^{d} = R \cap (W^{d} \times W^{d})\);
-
\(R_{\mathsf {N}}^{d} = R_{\mathsf {N}} \cap (W^d \times W^{d})\);
-
For all \(p \in Var\), \(V^{d}(p) = V(p) \cap W^{d}\).
The model \(M^d\) is treelike with finite depth. Further, Lem. 2.33 in [5] gives us:
From (2) we conclude that \(M^{d},w \models \phi \). Last, we show that \(M^{d}\) is a \(\mathsf {LAN}\)-model:
(R3) Let \(w,u,v \in W^{d}\) and assume \(wR_{\mathsf {N}}^{d}u\) and \(wR_{\mathsf {N}}^{d}v\). By definition of \(M^{d}\), we know that \(w,u,v \in W\) and that \(wR_{\mathsf {N}}u\) and \(wR_{\mathsf {N}}v\). Since the original model M satisfies property (R3), we have that \(u = v\).
(R4) Let \(w,u \in W^{d}\) and assume \(wR_{\mathsf {N}}^{d}u\). By definition of \(M^{d}\), we get \(w,u \in W\) and \(wR_{\mathsf {N}}u\). Since M satisfies property (R4), it follows that wRu. By the fact that \(w,u \in W^{d}\) and the definition of \(M^{d}\), we obtain \(wR^{d}u\).
(R5) Let \(w \in W^{d}\) and \(Agt = \{\alpha _{1}, ..., \alpha _{n}\}\). Suppose there are (not necessarily distinct) complex action-types \(\varDelta _{1}, {...}, \varDelta _{n} \in Act_{\mathsf {LAN}}\) s.t. for \(1 \le i \le n\) there exist \(u_{i} \in W^{d}\) s.t. \(wR^{d}u_{i}\) and \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{d}\). By definition of \(M^{d}\), it follows that \(wRu_{i}\) holds for each \(i \in \{1, {...}, n\}\) with \(height(u_{i}) \le deg(\phi )\). Since M satisfies (R5), we know there exists a \(v \in W\) s.t. wRv and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\). We know \(v \in W^{d}\) since \(height(v) = height(u_{i}) \le deg(\phi )\), which implies \(wR^{d}v\) and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{d} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{d}\) by definition of \(M^{d}\).
(R6) Let \(w \in W^{d}\) and \(\alpha _{i} \in Agt\). Assume there exists a \(v \in W^{d}\) s.t. \(wR^{d}v\) and \(v \in W_{\mathfrak {v}^{\alpha _i}}^{d}\). By definition of \(M^{d}\), we know that wRv holds with \(height(v) \le deg(\phi )\). Since M satisfies (R6), we know there exists a \(u \in W\) s.t. wRu and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\). Since \(height(u) = height(v) \le deg(\phi )\), it follows that \(u \in W^{d}\), \(wR^{d}u\), and \(u \in W^{d} - W_{\mathfrak {v}^{\alpha _i}}^{d}\).
Lemma 3
Every formula \(\phi \) satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth equal to \(deg(\phi )\), is satisfiable at the root of a treelike \(\mathsf {LAN}\)-model with finite depth and finite branching (i.e., \(\phi \) is satisfiable on a finite model).
Proof
Let \(M = (W, \{W_{\mathfrak {d}^{\alpha _{i}}_{j}}:\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\}, \{W_{\mathfrak {v}^{\alpha _i}}:\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\}, R, R_{\mathsf {N}},V)\) be a treelike \(\mathsf {LAN}\)-model with depth equal to \(deg(\phi )\) with root \(w\in W\) and assume \(M, w \models \phi \). Let \(Var(\phi )\) be the set of propositional variables occurring in \(\phi \). We define the set Atoms as \(Var(\phi ) \cup Wit \cup \{\mathfrak {v}^{\alpha _i}: \alpha _{i} \in Agt\}\). By Prop. 2.29 in [5], we know there are only a finite number of modal formulae (up to logical equivalence) built from the finite set Atoms with degree less than or equal to \(deg(\phi )\). We use \(\varTheta \) to denote this collection of (equivalence classes of) formulae.
Using \(\varTheta \), we first provide a selection procedure, similar to Thm. 2.34 of [5], to construct a finite model \(M^f\) and show that the root of this model satisfies \(\phi \). Last, we show that \(M^f\) is indeed a \(\mathsf {LAN}\)-model. We construct \(M^f\) as follows:
-
\(W^{f}\) is the set obtained from the selection procedure (below);
-
For all \(\mathfrak {d}^{\alpha _{i}}_{j} \in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {d}^{\alpha _{i}}_{j}}^{f} = W_{\mathfrak {d}^{\alpha _{i}}_{j}} \cap W^{f}\);
-
For all \(\mathfrak {v}^{\alpha _i}\in \mathcal {L}_{\mathsf {LAN}}\), \(W_{\mathfrak {v}^{\alpha _i}}^{f} = W_{\mathfrak {v}^{\alpha _i}} \cap W^{f}\);
-
\(R^{f} = R \cap (W^{f} \times W^{f})\);
-
\(R_{\mathsf {N}}^{f} = R_{\mathsf {N}} \cap (W^{f} \times W^{f})\);
-
For all \(p \in Var\), \(V^{f}(p) = V(p) \cap W^{f}\).
Selection Procedure. We build our domain \(W^{f}\) by selecting a sequence of states \(S_{0}, S_{1}, ..., S_{deg(\phi )}\) up to a height of \(deg(\phi )\), where \(S_{0} = \{w\}\). Each subscript i of \(S_{i}\) represents that the states contained in the associated set are at a height of i in the original model M. Suppose that the sets \(S_{0}\), \(S_{1}\), ..., \(S_{i}\) have already been chosen; we now explain how to select the set \(S_{i+1}\) with \(i+1 \le deg(\phi )\). For each formula \(\psi \in \varTheta \) equivalent to a formula of the form  or \(\langle \mathsf {N}\rangle \chi \) with \(deg(\psi ) \le deg(\phi ) - i\) s.t. \(M,u \models \psi \) for some \(u \in S_{i} \subseteq W\), we choose a \(v \in W\) s.t. uRv (or, \(uR_{\mathsf {N}}v\), depending on the modality in \(\psi \)) and \(M,v \models \chi \). We define the domain \(W^{f} = S_{0} \cup S_{1} \cup {...} \cup S_{deg(\phi )}\).
or \(\langle \mathsf {N}\rangle \chi \) with \(deg(\psi ) \le deg(\phi ) - i\) s.t. \(M,u \models \psi \) for some \(u \in S_{i} \subseteq W\), we choose a \(v \in W\) s.t. uRv (or, \(uR_{\mathsf {N}}v\), depending on the modality in \(\psi \)) and \(M,v \models \chi \). We define the domain \(W^{f} = S_{0} \cup S_{1} \cup {...} \cup S_{deg(\phi )}\).
The next statement is a consequence of this selection procedure [5, pp. 76–77]:
-
(3)
For any formula \(\psi \in \varTheta \) s.t. \(deg(\psi ) \le deg(\phi )\) and any world \(u \in W^{f}\) s.t.
$$\begin{aligned} height(u) \le deg(\phi ) - \deg (\psi ), M,u \models \psi \text { iff }M^{f},u \models \psi . \end{aligned}$$
From (3), together with \(M,w\models \phi \), \(\phi \in \varTheta \), \(deg(\phi ) \le deg(\phi )\), \(w \in W^{f}\!\), and \(height(w) \le deg(\phi )\), we infer \(M^{f},w \models \phi \). We show that \(M^{f}\) is an \(\mathsf {LAN}\)-model:
(R3) Let \(w, u, v \in W^{f}\) and assume \(wR_{\mathsf {N}}^{f}u\) and \(wR_{\mathsf {N}}^{f}v\). By definition of \(M^{f}\), \(wR_{\mathsf {N}}u\) and \(wR_{\mathsf {N}}v\) hold. Since the model M satisfies (R3), we obtain \(u=v\).
(R4) Let \(w, u \in W^{f}\) and assume \(wR_{\mathsf {N}}^{f}u\). By definition of \(M^{f}\), \(wR_{\mathsf {N}}u\) must hold. Since the original model M satisfies (R4), we have wRu, and because \(R^{f}\) is the set R restricted to \(W^{f}\), which contains w and u, we infer \(wR^{f}u\).
(R5) Let \(w \in W^{f}\) and let \(Agt = \{\alpha _{1}, {...}, \alpha _{n}\}\). Suppose there are (not necessarily distinct) complex action-types \(\varDelta _{1}, ..., \varDelta _{n}\in Act_{\mathsf {LAN}}\) s.t. for all \(1 \le i \le n\) there exists a \(u_{i} \in W^{f}\) s.t. \(wR^{f}u_{i}\) and \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}^{f}\). By definition of \(M^{f}\), this implies \(wRu_{i}\), \(u_{i} \in W_{t(\varDelta _{i}^{\alpha _{i}})}\), and \(height(u_{i}) \le deg(\phi )\) for each \(i \in \{1, {...}, n\}\). Since M satisfies (R5), we know that there exists a v such that wRv and \(v \in W_{t(\varDelta _{1}^{\alpha _{1}})} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}\), i.e.,  . Observe that because \(height(w) + 1 = height(u_{i}) \le deg(\phi )\) that \(1 \le deg(\phi )\), implying that
. Observe that because \(height(w) + 1 = height(u_{i}) \le deg(\phi )\) that \(1 \le deg(\phi )\), implying that  , because \(deg(\bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})) = 0\). Consequently, by the selection procedure a \(v' \in W\) such that \(wRv'\) and \(M, v' \models \bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})\) must have been selected and placed in \(S_{height(v')}\). Hence, there exists a \(v' \in W^{f}\) s.t. \(wR^{f}v'\) and \(v' \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{f} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{f}\).
, because \(deg(\bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})) = 0\). Consequently, by the selection procedure a \(v' \in W\) such that \(wRv'\) and \(M, v' \models \bigwedge _{1 \le i \le n}t(\varDelta _{i}^{\alpha _{i}})\) must have been selected and placed in \(S_{height(v')}\). Hence, there exists a \(v' \in W^{f}\) s.t. \(wR^{f}v'\) and \(v' \in W_{t(\varDelta _{1}^{\alpha _{1}})}^{f} \cap \cdots \cap W_{t(\varDelta _{n}^{\alpha _{n}})}^{f}\).
(R6) Let \(w \in W^{f}\), \(\alpha _{i}\in Agt\), and assume there is a \(v \in W^{f}\) s.t. \(wR^{f}v\) and \(v \in W_{\mathfrak {v}^{\alpha _i}}^{f}\). By definition of \(M^{f}\) we infer wRv and \(v \in W_{\mathfrak {v}^{\alpha _i}}\) with \(height(v) \le deg(\phi )\); hence, there exists a \(u \in W\) s.t. wRu and \(u \in W - W_{\mathfrak {v}^{\alpha _i}}\) with \(height(u) \le deg(\phi )\). It follows that  . Since \(height(w) = height(v) + 1 \le deg(\phi )\), we know that \(1 \le deg(\phi )\), and so,
. Since \(height(w) = height(v) + 1 \le deg(\phi )\), we know that \(1 \le deg(\phi )\), and so,  . By the selection procedure, a \(u' \in W\) s.t. \(wRu'\) and \(u' \in W - W_{\mathfrak {v}^{\alpha _i}}\) must have been chosen and placed in \(S_{height(u)}\); hence, \(u' \in W^{f}\), \(wR^{f}u'\), and \(u' \in W^{f} - W_{\mathfrak {v}^{\alpha _i}}^{f}\).
. By the selection procedure, a \(u' \in W\) s.t. \(wRu'\) and \(u' \in W - W_{\mathfrak {v}^{\alpha _i}}\) must have been chosen and placed in \(S_{height(u)}\); hence, \(u' \in W^{f}\), \(wR^{f}u'\), and \(u' \in W^{f} - W_{\mathfrak {v}^{\alpha _i}}^{f}\).
Theorem 2. \(\mathsf {LAN}\) has the finite (tree) model property, i.e., every satsifiable formula is satisfiable on a finite, treelike model.
Proof
Follows from Lemmas 1, 2, and 3.
Corollary 1. The satisfiability problem of \(\mathsf {LAN}\) is decidable.
Proof
By [5, Thm. 6.15], we know that if a normal modal logic is finitely axiomatizable and has the FMP, then it is decidable, which is the case for \(\mathsf {LAN}\).
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
van Berkel, K., Lyon, T., Olivieri, F. (2020). A Decidable Multi-agent Logic for Reasoning About Actions, Instruments, and Norms. In: Dastani, M., Dong, H., van der Torre, L. (eds) Logic and Argumentation. CLAR 2020. Lecture Notes in Computer Science(), vol 12061. Springer, Cham. https://doi.org/10.1007/978-3-030-44638-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-44638-3_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-44637-6
Online ISBN: 978-3-030-44638-3
eBook Packages: Computer ScienceComputer Science (R0)


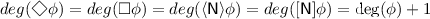 .
.