Abstract
We describe a technique to formally verify the security of masked implementations against side-channel attacks, based on elementary circuit transforms. We describe two complementary approaches: a generic approach for the formal verification of any circuit, but for small attack orders only, and a specialized approach for the verification of specific circuits, but at any order. We also show how to generate security proofs automatically, for simple circuits. We describe the implementation of CheckMasks, a formal verification tool for side-channel countermeasures. Using this tool, we formally verify the security of the Rivain-Prouff countermeasure for AES, and also the recent Boolean to arithmetic conversion algorithms from CHES 2017.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Masking Countermeasure. Masking is the most widely used countermeasure against side-channel attacks for block-ciphers and symmetric-key algorithms. In a first-order countermeasure, all intermediate variables x are masked into \(x'=x \oplus r\) where r is a randomly generated value. For such countermeasure, it is usually straightforward to verify its security against first-order attacks; namely it suffices to check that all intermediate variables have the uniform distribution, or at least that their distribution is independent from the key; therefore an attacker processing the side-channel leakage of intermediate variables separately (as in a first-order attack) does not get useful information.
However second-order attacks combining the leakage on \(x'\) and r can be mounted in practice, so it makes sense to design masking algorithms resisting higher-order attacks. This is done by extending Boolean masking to n shares with \(x=x_1 \oplus \cdots \oplus x_n\); in that case an implementation should be resistant against t-th order attacks, in which the adversary combines leakage information from at most \(t<n\) intermediate variables.
Security Proofs. In principle any countermeasure against high-order attacks should have a security proof, but such proof can be either missing, incomplete, or incorrect. In this paper we describe the construction of a tool, called CheckMasks, to automatically verify the security of high-order masking schemes.
The first step is to specify what it means for a masking countermeasure to be secure, i.e. what is the security model. Such formalization was initiated by Ishai et al. in [ISW03]. In this model, the adversary can probe at most t wires in the circuit, but he should not learn anything about the secret key. The approach for proving security is based on simulation: one must show that any set of t wires probed by the adversary can be perfectly simulated without the knowledge of the secret-key. This shows that the t probes do not bring any useful information to the attacker, since he could run this simulation by himself.
More precisely, the simulation technique consists in showing that any set of t probes can be perfectly simulated by the knowledge of only a proper subset of the input shares \(x_i\). At the beginning of the algorithm an original variable x is shared into n shares \(x_i\). When x is part of the secret-key, this pre-sharing cannot be probed by the adversary. Since any subset of at most \(n-1\) input shares \(x_i\) are uniformly and independently distributed, the simulation of the probed variables can be performed without knowing the secret-key.
The main result in [ISW03] is to show that any circuit C can be transformed into a new circuit \(C'\) of size \(\mathcal{O}(t^2 \cdot |C|)\) that is resistant against an adversary probing at most t wires in the circuit. The construction is based on secret-sharing every variable x into n shares with \(x=x_1 \oplus \cdots \oplus x_n\), and processing the shares in a way that prevents a t-limited adversary from leaning any information about the initial variable x, using \(n \ge 2t+1\) shares.
Formal Verification of Masking. The formal verification of the masking countermeasure was initiated by Barthe et al. in [BBD+15]. The authors describe an automated method to prove the security of masked implementation against t-th order attacks, for small values of t (in practice, \(t<5\)). The method only works for small values of t because the number of possible t-tuples of intermediate variables grows exponentially with t. To formally prove the security of a masking algorithm, the authors describe an algorithm to construct a bijection between the observations of the adversary (corresponding to a t-tuple of intermediate variables) and a distribution that is syntactically independent from the secret inputs; this implies that the adversary learns nothing from this particular t-tuple of intermediate variables. All possible t-tuples of intermediates variables are then examined by exhaustive search.
The authors obtain a formal verification of various masked implementations, up to second order masked implementation of AES, and up to 5-th order for the masked Rivain-Prouff multiplication [RP10]. In particular, the authors were able to rediscover some known attacks and discover new ways of attacking already broken schemes. Their approach is implemented in the framework of EasyCrypt [BDG+14], and relies on its internal representations of programs and expressions.
The main drawback of the previous approach is that it can only work for small orders t, since the running time is exponential in t. To overcome this problem, in a follow-up work [BBD+16], Barthe et al. studied the composition property of masked algorithms. In particular, the authors introduce the notion of strong simulatability, a stronger property which requires that the number of input shares necessary to simulate the observations of the adversary in a given gadget is independent from the number of observations made on output wires. This ensures some separation between the input and the output wires: no matter how many output wires must be simulated (to ensure the composition of gadgets), the number of input wires that must be known to perform the simulation only depends on the number of internal probes within the gadget.
The paper [BBD+16] has a number of important contributions that we summarize below. Firstly, the authors introduce the t-NI and t-SNI definitions. The t-NI security notion corresponds to the original security definition in the ISW probing model [ISW03]; it requires that any \(t_c \le t\) probes of the gadget circuit can be simulated from at most \(t_c\) of its input shares. The stronger t-SNI notion corresponds to the strong simulatability property mentioned above, in which the number of input shares required for the simulation is upper bounded by the number of probes \(t_c\) in the circuit, and is independent from the number of output variables \(|\mathcal {O}^{}|\) that must be simulated (as long as the condition \(t_c+ |\mathcal {O}^{}| <t\) is satisfied). We recall these definitions in Sect. 2, as they are fundamental in our paper.
The authors show that the t-SNI definition allows for securely composing masked algorithms; i.e. for a construction involving many gadgets, one can prove that the full construction is t-SNI secure, based on the t-SNI security of its components. The advantages are twofold: firstly the proof becomes modular and much easier to describe. Secondly as opposed to [ISW03] the masking order does not need to be doubled throughout the circuit, as one can work with \(n \ge t+1\) shares, instead of \(n \ge 2t+1\) shares. Since most gadgets have complexity \(\mathcal{O}(n^2)\), this usually gives a factor 4 improvement in efficiency. In [BBD+16], the authors prove the t-SNI property of several useful gadgets: the multiplication of Rivain-Prouff [RP10], the mask refreshing based on the same multiplication algorithm, and the multiplication between linearly dependent inputs from [CPRR13].
Moreover, in [BBD+16] the authors also machine-checked the multiplication of Rivain-Prouff and the multiplication-based mask refreshing in the EasyCrypt framework [BDG+14]. The main point is that their machine verification works for any order, whereas in [BBD+15] the formal verification could only be performed at small orders t. However, the approach seems difficult to understand (at least for a non-expert in formal methods), and when reading [BBD+16] it is far from obvious how the automated verification of the countermeasure can be implemented concretely; this seems to require a deep knowledge of the EasyCrypt framework.
Finally, the authors built an automated approach for verifying that an algorithm constructed by composing provably secure gadgets is itself secure. They also implemented an algorithm for transforming an input program P into a program \(P'\) secure at order t; their algorithm automatically inserts mask refreshing gadgets whenever required.
Our Contributions. Our main goal in this paper is to simplify and extend the formal verification results from [BBD+15, BBD+16]. We describe two complementary approaches: a generic approach for the formal verification of any circuit, but for small attack orders only (as in [BBD+15]), and a specialized approach for the verification of specific circuits, but at any order (as in [BBD+16]).
For the generic verification of countermeasures at small orders, we use a different formal language from [BBD+15]. In particular we represent the underlying circuit as nested lists, which leads to a simple and concise implementation in Common Lisp, a programming language well suited to formal manipulations. We are then able to formally verify the security of the Rivain-Prouff countermeasure with very few lines of code. Our running times for formal verification are similar to those in [BBD+15]. Thanks to this simpler approach, we could also extend [BBD+15] to handle a combination of arithmetic and Boolean operations, and we have formally verified the security of the recent Boolean to arithmetic conversion algorithm from [Cor17c]. To perform these formal verifications we describe the implementation of CheckMasks, our formal verification tool for side-channel countermeasures.
For the verification of specific gadgets at any order (instead of small orders only with the generic approach), our technique is quite different from [BBD+16] and consists in applying elementary transforms to the circuit, until the t-NI or t-SNI properties become straightforward to verify. We show that for a set of well-chosen elementary transforms, the formal verification time becomes polynomial in t (instead of exponential with the generic approach); this implies that the formal verification can be performed at any order. Using our CheckMasks tool, we provide a formally verified proof of the t-SNI property of the multiplication algorithm in the Rivain-Prouff countermeasure, and of the mask refreshing based on the same multiplication algorithm; in both cases the running time of the formal verification is polynomial in the number of shares n.
Finally, we show how to get the best of both worlds, at least for simple circuits: we show how to automatically apply the circuit transforms that lead to a polynomial time verification, based on a limited set of generic rules. Namely we identify a set of three simple rules that enable to automatically prove the t-SNI property of the multiplication based mask refreshing, and also two security properties of mask refreshing considered in [Cor17c].
Source Code. The source code of our CheckMasks verification tool is publicly available at [Cor17a], under the GPL v2.0 license.
2 Security Properties
In this section we recall the t-NI and t-SNI security definitions from [BBD+16]. For simplicity we only provide the definitions for a simple gadget taking as input a single variable x (given by n shares \(x_i\)) and outputting a single variable y (given by n shares \(y_i\)). Given a vector of n shares \((x_i)_{1 \le i \le n}\), we denote by \(x_{|I}:=(x_i)_{i \in I}\) the sub-vector of shares \(x_i\) with \(i \in I\). In general we wish to simulate any subset of intermediate variables of a gadget from the knowledge of as few \(x_i\)’s as possible.
Definition 1
(t-NI security). Let G be a gadget taking as input \((x_i)_{1 \le i \le n}\) and outputting the vector \((y_i)_{1 \le i \le n}\). The gadget G is said t-NI secure if for any set of \(t_c \le t\) intermediate variables, there exists a subset I of input indices with \(|I| \le t_c\), such that the \(t_c\) intermediate variables can be perfectly simulated from \(x_{|I}\).
Definition 2
(t-SNI security). Let G be a gadget taking as input \((x_i)_{1 \le i \le n}\) and outputting \((y_i)_{1 \le i \le n}\). The gadget G is said t-SNI secure if for any set of \(t_c\) intermediate variables and any subset \(\mathcal {O}^{}\) of output indices such that \(t_c+|\mathcal {O}^{}| \le t\), there exists a subset I of input indices with \(|I| \le t_c\), such that the \(t_c\) intermediate variables and the output variables \(y_{|\mathcal {O}^{}}\) can be perfectly simulated from \(x_{|I}\).
The t-NI security notion corresponds to the original security definition in the ISW probing model, in which \(n \ge 2t+1\) shares are required. The stronger t-SNI notion allows for securely composing masked algorithms, and allows to prove the security with \(n \ge t+1\) shares only [BBD+16]. The difference between the two notions is as follows: in the stronger t-SNI notion, the size of the input shares subset I can only depend on the number of internal probes \(t_c\) and is independent of the number of output variables \(|\mathcal {O}^{}|\) that must be simulated (as long as the condition \(t_c+ |\mathcal {O}^{}| \le t\) is satisfied). The t-SNI security notion is very convenient for proving the security of complex constructions, as one can prove that the t-SNI security of a full construction based on the t-SNI security of its components.
3 Formal Verification of Generic Circuits for Small Order
In this section, we show that the t-NI and t-SNI properties can be easily verified formally for any Boolean circuit, using a generic approach. As in [BBD+15] the complexity of the formal verification is exponential in the number of shares n, so this can only work for small n.
3.1 The RefreshMasks Algorithm
To illustrate our approach we first consider the RefreshMasks algorithm below from [RP10]; see Fig. 1 for an illustration.

We first recall a straightforward property of the RefreshMasks algorithm: when the intermediate variables of the algorithm are not probed, any subset of \(n-1\) output shares \(y_i\) of RefreshMasks is uniformly and independently distributed. In the next section, we show how to formally verify this property.
Lemma 1
Let \((y_i)_{1 \le i \le n}\) be the output of RefreshMasks. Any subset of \(n-1\) output shares \(y_i\) is uniformly and independently distributed.
3.2 Formal Verification of Circuits
Circuit Representation. We represent a circuit with nested lists, using the prefix notation. Consider for example the circuit taking as input x and y and outputting \(x \oplus y\); we represent it as  . Similarly the circuit computing \(x \cdot y\) is represented as
. Similarly the circuit computing \(x \cdot y\) is represented as  . To represent more complex circuits the lists are recursively nested. For example, to represent the circuit \(x \cdot (y \oplus z)\), we write
. To represent more complex circuits the lists are recursively nested. For example, to represent the circuit \(x \cdot (y \oplus z)\), we write  . If a circuit has many outputs, we represent the list of outputs without any prefix operator; for example, the circuit outputting \((x \oplus y,x\cdot y)\) can be represented as
. If a circuit has many outputs, we represent the list of outputs without any prefix operator; for example, the circuit outputting \((x \oplus y,x\cdot y)\) can be represented as  .
.
It is easy to write a program in Common Lisp that generates the circuit corresponding to RefreshMasks; we refer to [Cor17a] for the source code. For example, we obtain for \(n=3\) input shares:

which corresponds to \(y_1=r_1 \oplus x_1\), \(y_2=r_2 \oplus x_2\) and \(y_3=r_2 \oplus (r_1 \oplus x_3)\). Note that the above  function in Common Lisp takes as input a list of n shares (here \(n=3\)) and outputs a list of n shares; therefore it can be easily composed with other such Common Lisp functions to create more complex circuits.
function in Common Lisp takes as input a list of n shares (here \(n=3\)) and outputs a list of n shares; therefore it can be easily composed with other such Common Lisp functions to create more complex circuits.
List Substitutions. We now explain how to formally verify Lemma 1. Consider for example the two output variables  and
and  from above. We would like to show that these two variables are uniformly and independently distributed. Since the random
from above. We would like to show that these two variables are uniformly and independently distributed. Since the random  is used only once in those two outputs, it can play the role of a one-time pad, and we can perform the following substitution in the second output:
is used only once in those two outputs, it can play the role of a one-time pad, and we can perform the following substitution in the second output:

Namely, since  is used only once, the distribution of
is used only once, the distribution of  is the same as the distribution of
is the same as the distribution of  . Starting with the above list of two output variables, we can perform the following sequence of elementary substitutions:
. Starting with the above list of two output variables, we can perform the following sequence of elementary substitutions:

The first substitution is possible because  is used only once, and the second substitution is possible because
is used only once, and the second substitution is possible because  is used only once after the first substitution. Since we have obtained two distinct randoms
is used only once after the first substitution. Since we have obtained two distinct randoms  at the end, the two output variables are uniformly and independently distributed, as required.
at the end, the two output variables are uniformly and independently distributed, as required.
Formal Verification. To formally verify Lemma 1, it suffices to consider all possible subsets of \(n-1\) output shares \(y_i\) among n, and check that for every subset, we obtain after a series of elementary substitutions a list of \(n-1\) distinct randoms. These substitutions are easy to implement in Common Lisp. Namely it suffices to perform a tree search to count the number of times a given random  is used, and if a random
is used, and if a random  is used only once, we can then perform the substitution:
is used only once, we can then perform the substitution:

In the particular case of Lemma 1, there are only n subsets to consider, so the formal verification is performed in polynomial time. We obtain for example for \(n=3\):

The above transcript shows that Lemma 1 is formally verified for \(n=3\); namely in all 3 possible cases, after a sequence of elementary substitutions, we obtain a list of 2 distinct randoms, showing that the two output variables are uniformly and independently distributed; see [Cor17a] for the source code.
3.3 Security Properties of RefreshMasks
In this section we show how to formally verify some existing properties of RefreshMasks. We first consider the straightforward t-NI property, for \(t=n-1\).
Lemma 2
(t-NI of RefreshMasks). Let \((x_i)_{1\le i \le n}\) be the input of RefreshMasks and let \((y_i)_{1 \le i \le n}\) be the output. For any set of \(t_c \le n-1\) intermediate variables, there exists a subset I of input indices such that the \(t_c\) intermediate variables can be perfectly simulated from \(x_{|I}\), with \(|I| \le t_c\).
Formal Verification of the \(\varvec{t}\)-NI Property of RefreshMasks. The t-NI property of RefreshMasks is straightforward because in the definition of RefreshMasks, any intermediate variable depends on at most one input \(x_i\); therefore any subset of \(t_c\) probes can be perfectly simulated from the knowledge of at most \(t_c\) inputs \(x_i\). Consider for example RefreshMasks with \(n=3\) as previously:

If we probe the two intermediate variables  and
and  , then the knowledge of the two inputs
, then the knowledge of the two inputs  and
and  is sufficient for the simulation; moreover we cannot perform any substitution because the random
is sufficient for the simulation; moreover we cannot perform any substitution because the random  is used twice. On the other hand if we probe the two variables
is used twice. On the other hand if we probe the two variables  and
and  , we can perform the substitution:
, we can perform the substitution:

showing that the knowledge of the input variables  and
and  is not required for that simulation.
is not required for that simulation.
More generally, to verify the t-NI property of any circuit, it suffices to exhaustively consider all possible \(t_c\)-tuples of intermediate variables for all \(t_c \le t\), and verify that after a set of elementary substitutions the knowledge of at most \(t_c\) input variables is needed for the simulation of the \(t_c\)-tuple.
Other Security Properties of RefreshMasks. We perform a formal verification of several non-trivial properties of RefreshMasks that were used to prove the security of the Boolean to arithmetic conversion algorithm from [Cor17c]; the full version of this paper [Cor17b]. The first property is the following: if the output \(y_n\) is among the \(t_c\) probed variables, then we can simulate those \(t_c\) probed variables with \(t_c-1\) input shares \(x_i\) only, instead of \(t_c\) as in Lemma 2. This property was crucial for obtaining a provably secure Boolean to arithmetic conversion algorithm in [Cor17c].
Lemma 3
( RefreshMasks [Cor17c]). Let \(x_1,\ldots ,x_n\) be the input of a RefreshMasks where the randoms are accumulated on \(x_n\), and let \(y_1,\ldots ,y_n\) be the output. Let \(t_c\) be the number of probed variables, with \(t_c <n\). If \(y_n\) is among the probed variables, then there exists a subset I such that all probed variables can be perfectly simulated from \(x_{|I}\), with \(|I| \le t_c-1\).
As previously, to perform a formal verification of Lemma 3, it suffices to consider all possible \(t_c\)-tuples of intermediate variables (where \(y_n\) is part of the \(t_c\)-tuple) and show that after a sequence of elementary substitutions, there remains at most \(t_c-1\) input variables. In the full version of this paper [Cor17b], we argue that it is actually sufficient to perform such verification for \(t_c=n-1\) only, instead of all \(1 \le t_c \le n-1\). The timings of formal verification are summarized in Table 1. Although we are only able to verify Lemma 3 for small values of n, this still provides some confidence in the correctness of Lemma 3 for any n. We refer to the full version of this paper [Cor17b] for some other properties of RefreshMasks and their formal verification for small values of n.
3.4 Formal Verification of t-SNI Properties: The FullRefresh and SecMult Algorithms
It is easy to see that that the RefreshMasks algorithm from the previous section does not achieve the stronger t-SNI property, as already observed in [BBD+16]. Namely one can probe the output \(y_1=r_1 \oplus x_1\) and the internal variable \(y_{n,1}=r_1 \oplus x_n\). This gives \(y_1 \oplus y_{n,1}=x_1 \oplus x_n\) and therefore the knowledge of both inputs \(x_1\) and \(x_n\) is required for the simulation, whereas only \(t_c=1\) internal variable has been probed.
The FullRefresh Algorithm. We recall below an improved mask refreshing algorithm that does satisfy the t-SNI property for \(t=n-1\), as shown in [BBD+16]. The algorithm FullRefresh is based on the masked multiplication from [ISW03] and was already used in [ISW03, DDF14]. Note that the algorithm has complexity \(\mathcal{O}(n^2)\) instead of \(\mathcal{O}(n)\) for RefreshMasks.

Lemma 4
(t-SNI of FullRefresh [BBD+16]). Let \((x_i)_{1 \le i \le n}\) be the input shares of the \(\mathsf{FullRefresh}\) operation, and let \((y_i)_{1 \le i \le n}\) be the output shares. For any set of \(t_c\) intermediate variables and any subset \(\mathcal {O}^{}\) of output shares such that \(t_c+|\mathcal {O}^{}|<n\), there exists a subset I of indices with \(|I| \le t_c\), such that the \(t_c\) intermediate variables as well as the output shares \(y_{|\mathcal {O}^{}}\) can be perfectly simulated from \(x_{|I}\).
Formal Verification of FullRefresh. In the following, we describe the formal verification of Lemma 4 using our CheckMasks tool. As previously we first implement the FullRefresh algorithm in Common Lisp; for example, we get the following output for \(n=3\) shares:

Using our CheckMasks tool, the \((n-1)\)-SNI property in Lemma 4 can be easily verified for small values of n. Namely it suffices to compute the list of all \((n-1)\)-tuples of intermediate variables (including the outputs \(y_i\)) and check that every such \((n-1)\)-tuple can be perfectly simulated from the knowledge of at most \(t_c\) inputs \(x_i\), where \(t_c\) is the number of non-output variables in the \((n-1)\)-tuple. Consider for example the two variables  and
and  in the circuit above for \(n=3\); since
in the circuit above for \(n=3\); since  is an output variable, the simulation must be performed using at most a single input \(x_i\). We obtain using elementary substitutions:
is an output variable, the simulation must be performed using at most a single input \(x_i\). We obtain using elementary substitutions:

and therefore no input \(x_i\) is actually needed to simulate those two variables. However if we probe the two variables  and
and  , we can perform the substitutions:
, we can perform the substitutions:

and therefore the knowledge of  is required for the simulation.Footnote 1 Note that the running time to consider all possible \((n-1)\)-tuples of intermediate variables is exponential in n. We summarize in Table 2 the running time of the formal verification of FullRefresh, up to \(n=6\). In Sect. 5 we will show how to formally verify Lemma 4 in time polynomial in n, so that the formal verification can be performed for any number of shares n used in practice.
is required for the simulation.Footnote 1 Note that the running time to consider all possible \((n-1)\)-tuples of intermediate variables is exponential in n. We summarize in Table 2 the running time of the formal verification of FullRefresh, up to \(n=6\). In Sect. 5 we will show how to formally verify Lemma 4 in time polynomial in n, so that the formal verification can be performed for any number of shares n used in practice.
The Rivain-Prouff Countermeasure. The Rivain-Prouff countermeasure for AES is based on an extension over \({\mathbb F}_{2^k}\) of the masked AND gate from [ISW03]. It enables to securely compute a n-sharing of the product \(c = a \cdot b\) over \({\mathbb F}_{2^k}\), from an n-sharing of a and b. The algorithm was proven t-SNI in [BBD+16]. In the full version of this paper [Cor17b], we recall the corresponding SecMult algorithm, and we show how to formally verify its t-SNI property for small values of n, for \(t=n-1\).
4 Formal Verification of Boolean to Arithmetic Conversion
In this section we show how to extend [BBD+15] to handle a combination of arithmetic and Boolean operations. This enables to formally verify the security of the high-order Boolean to arithmetic conversion algorithm recently described at CHES 2017 [Cor17c], with a t-SNI security proof for \(n \ge t+1\). The algorithm can be seen as a generalization of Goubin’s algorithm [Gou01] to any order, still with a complexity independent of the register size k. Although the algorithm has complexity \(\mathcal{O}(2^n)\), instead of \(\mathcal{O}(n^2 \cdot k)\) in [CGV14], for small values of n it is an order of magnitude more efficient. The algorithm takes as input n Boolean shares \(x_i\) such that
and using a recursive algorithm computes n arithmetic shares \(D_i\) such that
Sequence of operations in the Boolean to arithmetic conversion algorithm from [Cor17c].
Boolean to Arithmetic Conversion. The algorithm from [Cor17c] is based on the affine property of the function \(\varPsi (x,r) := (x \oplus r)-r \pmod {2^k}\). As illustrated in Fig. 2 the algorithm is recursive and makes two recursive calls to the same algorithm C with \(n-1\) inputs. For \(n=2\) one uses a t-SNI variant of Goubin’s algorithm:
For \(n \ge 3\) the algorithm works as follows. One first performs a mask refreshing R, while expanding the \(x_i\)’s to \(n+1\) shares. One obtains, from the definition of the \(\varPsi \) function:
From the affine property of the \(\varPsi \) function, the left term can be decomposed into the xor of n shares \(\varPsi (x_1,x_i)\) for \(2 \le i \le n+1\), where the first share is \((\overline{n \wedge 1}) \cdot x_{1} \oplus \varPsi (x_{1},x_2)\):
We obtain that x is the arithmetic sum of two terms, each with n Boolean shares; this corresponds to the two branches in Fig. 2. One then performs a mask refreshing R on both branches, and then a compression function F that simply xors the last two shares, so there remains only \(n-1\) shares on both branches. One can then apply the Boolean to arithmetic conversion C recursively on both branches, taking as input \(n-1\) Boolean shares (instead of n), and outputting \(n-1\) arithmetic shares; we obtain:
Eventually it suffices to do some additive grouping to obtain n arithmetic shares as output, as required:
We refer to [Cor17c] for the details of the algorithm. The algorithm is proven t-SNI secure with \(n \ge t+1\) shares in [Cor17c].
Algorithm Representation. In Sect. 3.3 we have described a formal verification of the security properties of RefreshMasks that are required for the security proof of the above Boolean to arithmetic conversion algorithm in [Cor17c]. However this provides only a partial verification of the algorithm, since in that case the adversary is restricted to only probing the Boolean operations performed within the RefreshMasks. To obtain a full verification, we must consider an adversary who can probe any variable in the Boolean to arithmetic algorithm. In that case the formal verification becomes more complex as we must handle both Boolean and arithmetic operations.
Since in our nested list representation we have already using the \(+\) operator for the xor, we use the ADD keyword to denote the arithmetic sum. For example, the final additive grouping can be represented as:

which corresponds to the three arithmetic shares \(D_1=A_1+B_1 \pmod {2^k}\), \(D_2=A_2\) and \(D_3=B_2\). We also use the PSI operator to denote the application of the \(\varPsi \) function. For example, the Boolean to arithmetic conversion algorithm for \(n=2\) gives from (2) and (3):

Simplification Rules. Given a list of intermediate variables that must be simulated, as previously we must use a set of simplification rules to determine how many inputs \(x_i\) are required for the simulation. For the verification of Boolean circuits in the previous section, this was relatively straightforward as we had essentially a single simplification rule, namely replacing \(x \oplus r\) by r when the random r appears only once in the intermediate variables. However when combining arithmetic and Boolean operations the formal verification becomes more complex and we used the following simplification rules. We illustrate every rule by an example that can be run from the source code [Cor17a].
-
Rule 1: when \(\omega =x_1+x_2 \bmod {2^k}\) must be simulated, simulate both \(x_1\) and \(x_2\).

-
Rule 2: from the affine property of the function \(\varPsi \), replace \(\varPsi (x,y) \oplus \varPsi (x,z)\) by \(x \oplus \varPsi (x,y \oplus z)\).

-
Rule 3: from the definition of \(\varPsi \), replace \(\varPsi (x,y)\) by \((x \oplus y)-y \bmod {2^k}\); we denote by SUB the arithmetic subtraction.

-
Rule 4: when a random r is used only once, replace \(x \oplus r\) by r, and similarly for \(x+r \bmod {2^k}\) and \(x-r \bmod {2^k}\). This is an extension of the rule given by (1).
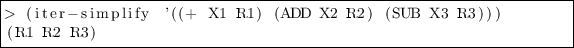
-
Rule 5: when a random r is not used in two intermediate variables \(e_1\) and \(e_2\), replace the simulation of \((e_1 \oplus r,e_2 \oplus r)\) by the simulation of \((r,(e_1 \oplus r) \oplus e_2)\); this corresponds to the change of variable \(r'=e_1 \oplus r\).
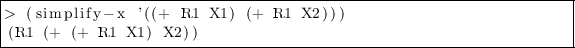
-
Rule 6: when \(\varPsi (x_1,x_2)\) must be simulated, simulate both \(x_1\) and \(x_2\).

We note that the order in which the rules are applied matters. For example, once Rule 3 has been applied, Rule 2 cannot be applied to the same expression, because the PSI operator has been replaced by SUB. One must therefore use the right strategy for the application of the rules; an overview is provided in Fig. 3. In particular, we only apply Rule 3 if subsequently applying Rule 4 enables to eliminate the SUB operator, and Rule 6 is only applied as a last resort, when other rules have failed.
Formal Verification. In order to verify the t-SNI property of the Boolean to arithmetic algorithm, as previously we must check that for all possible \((n-1)\)-tuples of intermediate variables (including the outputs \(D_i\)), the number of input variables \(x_i\)’s that remain after the application of the above rules is always \(\le t_c\), where \(t_c\) is the number of non-output variables in the \((n-1)\)-tuple.
We summarize in Table 3 the timings of formal verification for the algorithm in [Cor17c]. Note that the Boolean to arithmetic conversion algorithm has complexity \(\mathcal{O}(2^n)\), and therefore the number of possible \((n-1)\)-tuples of intermediate variables is \(\mathcal{O}(2^{n^2})\); that is why we could only perform the formal verification up to \(n=5\).
5 Formal Verification in Polynomial Time
The main drawback of the previous approach is that it has exponential complexity in the number of shares n, because the number of t-tuples to consider grows exponentially with n. In this section we describe a new approach for proving the security of a side-channel countermeasure. Instead of performing a simulation of the probed variables as in [ISW03], our approach consists in applying a sequence of elementary circuit transforms, until the transformed circuit becomes so simple that the security property becomes straightforward to verify. The main advantage is that in the context of formal verification, our new approach seems much easier to verify formally than the classical simulation-based approach from [ISW03]. For Boolean circuits our technique is based on the following two elementary transforms:
-
The Random-zero transform: we set to 0 a subset of the randoms \(r_i\) used in the circuit.
-
The One-time-pad transform: if a random r appears only once in a circuit, and moreover r is not probed, we can replace any variable \(x \oplus r\) by r.
The Random-Zero Transform. Our first circuit transformation consists in setting to 0 a subset of the randoms \(r_i\) used in the circuit. The transform only applies to additively masked circuits.
Definition 3
(Additive masking). Let C be a circuit taking as input \(x_1,\ldots , \) \(x_n\). We say that C is additively masked if every intermediate variable y in the circuit can be written as \(y=f(x_1,\ldots ,x_n) + g(r_1,\ldots ,r_n)\), where g is a linear function.
For example, the circuit computing \(y=x_1 \cdot x_2 + r_1 + r_2\) is additively masked, while the circuit computing \(y=x_1 \cdot r_1\) is not. Most side-channel countermeasures for block-ciphers are additively masked. In particular, this holds for the RefreshMasks, FullRefresh and SecMult algorithms considered in the previous sections. The following lemma shows that it is sufficient to consider the security of a simpler circuit \(C_0\) where a subset of the randoms are fixed to 0. Namely if there is an attack against the original circuit C, then the same attack applies against \(C_0\); see the full version of this paper [Cor17b] for the proof.
Lemma 5
(Random-zero transform). Let C be an additively masked circuit and let \(C_0\) be the same circuit as C but with a subset of the randoms fixed to 0. Anything an adversary can compute from a set of probes in C, he can compute from the same set of probes in the circuit \(C_0\).
Remark 1
Lemma 5 does not hold for general circuits; consider for example the circuit taking as input sk and outputting \((sk \cdot r,r)\); when considering the output only, the circuit would be secure when r is fixed to 0, but the output leaks the secret sk whenever \(r \ne 0\).
Application: \(\varvec{t}\)-NI of RefreshMasks. The t-NI property of RefreshMasks, as stated in Lemma 2, is easily verified formally using the Random-zero transform. Namely, if we fix all randoms of RefreshMasks to 0, we obtain the identity function, which is trivially t-NI. For example, we obtain for \(n=4\):

Note that the verification is performed in polynomial time in n, while in the generic approach the complexity would be exponential in n when examining all possible t-tuples.
The One-Time Pad Transform. The One-time Pad transform is defined as follows: if a random r is used only once in a circuit, and moreover r is not probed, then we can replace the variable \(x \oplus r\) by r. Note that in principle the variable x can still be probed, so it must not be removed from the circuit.
We can assume that a certain random r has not been probed when we have an upper bound on the number of probes in the circuit, as it is the case for the t-NI and t-SNI properties. For example, if a circuit contains n randoms \(r_i\) but the adversary has only access to \(t=n-1\) probes, then we are guaranteed that at least one of the random \(r_i\) has not been probed, and we can apply the One-time Pad transform on this random. The proof technique then consists in considering all possible n cases separately (corresponding to the non-probed \(r_i\), for \(1 \le i \le n\)), and then applying the admissible One-time Pad transform in each case.
Formal Verification in Polynomial-Time. More generally, the proof strategy is to perform a sequence of elementary circuit transforms until we obtain a simple circuit C for which the t-NI or t-SNI properties is straightforward to verify. In the full version of this paper [Cor17b] we illustrate this approach by providing a formal verification of the same security properties of the RefreshMasks, FullRefresh and SecMult algorithms as considered in Sect. 3, but this time with complexity polynomial in n, instead of exponential. This implies that the security of these algorithms can be formally verified for any value of n for which the countermeasure would be used in practice. We refer to [Cor17a] for the source code of the formal verification.
6 Towards Automatic Generation of Security Proofs
The drawback of the previous approach is that for the security verification to happen in polynomial time, we must select ourselves the right sequence of circuit transforms. Instead we would like to have the circuit transforms being selected automatically by our verification tool, based on a limited set of elementary rules, and still in polynomial-time.
In the following, we show that this can be achieved for simple circuits based on the three following rules. We denote by P the property that must be checked; for example, for t-NI security, the property P would require that any t-tuple of intermediate variables is simulatable from a subset of the inputs \(x_{|I}\), with \(|I| \le t\). Below we denote by \(C_{otp}\) the circuit \(y_i=x_i \oplus r_i\) for \(1 \le i \le n\) (see the full version of this paper [Cor17b]). We assume that the property P is already verified by \(C_{otp}\), so that P does not need to be verified explicitly for \(C_{otp}\).
-
(R1)
Perform a loop to select and remove the subset of the circuit that is unprobed.
-
(R2)
Apply the random-zero transform, except on randoms used only once in the circuit.
-
(R3)
Check whether the resulting circuit is equal to \(C_{otp}\). Otherwise check the property P for all possible t-tuple of probes.
We show in the full version of this paper [Cor17b] that from the three above rules, we can formally verify in polynomial time the main properties of RefreshMasks and FullRefresh considered in this paper.
Notes
- 1.
This is still according to the t-SNI property, because
 is an output variable and therefore \(t_c=1\).
is an output variable and therefore \(t_c=1\).
References
Barthe, G., Belaïd, S., Dupressoir, F., Fouque, P.-A., Grégoire, B., Strub, P.-Y.: Verified proofs of higher-order masking. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 457–485. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_18. https://eprint.iacr.org/2015/060
Barthe, G., Belaïd, S., Dupressoir, F., Fouque, P.-A., Grégoire, B., Strub, P.-Y., Zucchini, R.: Strong non-interference and type-directed higher-order masking. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016, pp. 116–129 (2016). Publicly available at https://eprint.iacr.org/2015/506.pdf. See also a preliminary version, under the title “Compositional Verification of Higher-Order Masking: Application to a Verifying Masking Compiler”, publicly available at https://eprint.iacr.org/2015/506/20150527:192221
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: a tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Coron, J.-S., Großschädl, J., Vadnala, P.K.: Secure conversion between boolean and arithmetic masking of any order. In: Batina, L., Robshaw, M. (eds.) CHES 2014. LNCS, vol. 8731, pp. 188–205. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44709-3_11
Coron, J.-S.: CheckMasks: formal verification of side-channel countermeasures (2017). Publicly available at https://github.com/coron/checkmasks
Coron, J.-S.: Formal verification of side-channel countermeasures via elementary circuit transformations. Cryptology ePrint Archive, Report 2017/879 (2017). https://eprint.iacr.org/2017/879
Coron, J.-S.: High-order conversion from Boolean to arithmetic masking. In: Fischer, W., Homma, N. (eds.) CHES 2017. LNCS, vol. 10529, pp. 93–114. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66787-4_5
Coron, J.-S., Prouff, E., Rivain, M., Roche, T.: Higher-order side channel security and mask refreshing. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 410–424. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43933-3_21
Duc, A., Dziembowski, S., Faust, S.: Unifying leakage models: from probing attacks to noisy leakage. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 423–440. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_24
Goubin, L.: A sound method for switching between boolean and arithmetic masking. In: Koç, Ç.K., Naccache, D., Paar, C. (eds.) CHES 2001. LNCS, vol. 2162, pp. 3–15. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44709-1_2
Ishai, Y., Sahai, A., Wagner, D.: Private circuits: securing hardware against probing attacks. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 463–481. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_27
Rivain, M., Prouff, E.: Provably secure higher-order masking of AES. In: Mangard, S., Standaert, F.-X. (eds.) CHES 2010. LNCS, vol. 6225, pp. 413–427. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15031-9_28
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Coron, JS. (2018). Formal Verification of Side-Channel Countermeasures via Elementary Circuit Transformations. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)










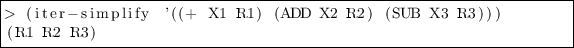
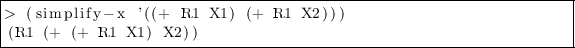


 is an output variable and therefore
is an output variable and therefore