Joint inspection and inventory control for deteriorating items with time-dependent demand and deteriorating rate

Abstract

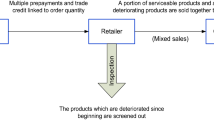
In this paper, we consider inventory control problems for deteriorating items with maximum serviceable lifetime under mixed sales situation, both of the demand and the deterioration rate are depending on time. A model is presented to formulate the process of mixed sales that deteriorated items are sold to consumers together with serviceable items, where penalty cost for the sales of deteriorated products is included. From the literature search, this study is one of the first researches on the joint inspection and inventory control policies under the mixed sales situation with time-dependent demand and deterioration rate. An additional ordering contract is designed to improve the inventory holder’s profit. The optimal ordering time and ordering quantities are characterized for the additional ordering contract. We show that it would be more beneficial for the inventory holder to employ an additional order. Furthermore, two different inspection policies are considered in this study: (i) one inspection during the cycle; (ii) continuous monitoring in the cycle. The numerical results show that the net profit would increase if one inspection or continuous monitoring is conducted. These results provide useful insights to guide decision-making in inventory control problems of deteriorating products.

Appendix

1.1 Proof of Proposition 1

Based on Eq. (10), it has

$$\begin{aligned} \displaystyle \frac{\partial {\varPi }_1}{\partial T_1}=\displaystyle \frac{D[p+k+h(1+m)]}{m(1+m)}\left[ T_1-\displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)}\right] (T_1-m). \end{aligned}$$

Set $\displaystyle \frac{\partial {\varPi }_1}{\partial T_1}=0,$ it has $T_1=\frac{(p-c)(1+m)}{p+k+h(1+m)}$ or $T_1=m.$

• Case 1 If $p<c(1+m)+hm(1+m)+km,$ then $\frac{(p-c)(1+m)}{p+k+h(1+m)}<m.$ Then it has

  $$\begin{aligned} \displaystyle \frac{\partial {\varPi }_1}{\partial T_1}\ge 0&\text {when}&T_1 \in \left( 0,\displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)}\right] \\ \displaystyle \frac{\partial {\varPi }_1}{\partial T_1}< 0&\text {when}&T_1 \in \left( \displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)},m\right] . \end{aligned}$$

  Therefore ${\varPi }_1$ reaches its maximum at $T_1^*=\displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)}.$

• Case 2 If $p\ge c(1+m)+hm(1+m)+km,$ then $\frac{(p-c)(1+m)}{p+k+h(1+m)}\ge m.$ Then it has

  $$\begin{aligned} \displaystyle \frac{\partial {\varPi }_1}{\partial T_1}\ge 0&\text {when}&T_1 \in \left( 0,m\right] . \end{aligned}$$

  Therefore ${\varPi }_1$ reaches its maximum at $T_1^*=m.$

The proof is completed.

1.2 Proof of Proposition 2

Suppose that $c=b.$ Denote $m_1=m+\frac{(p-c)(1+m)}{p+k+h(1+m)}.$ Based on Eq. (14), it has

$$\begin{aligned} \displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}= & {} \displaystyle \frac{-D[p+k+h(1+m)]}{m(1+m)}(T-2t_1)(T-m_1) \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}= & {} \displaystyle \frac{2D[p+k+h(1+m)]}{m(1+m)}(T-m_1). \end{aligned}$$

• Case 1 If $p<c(1+m)+km+hm(1+m),$ then $\frac{(p-c)(1+m)}{p+k+h(1+m)}<m$ and $m_1<2m.$

  • (a) If $0<T<m_1,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Set $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}=0$, it yields $t_1^*=\displaystyle \frac{T}{2}.$

  • (b) If $T=m_1,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}=0$ and $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}=0.$ Since it requires that $0<t_1\le m$ and $0<T-t_1\le m,$ we have $T-m\le t_1^* \le m.$

  • (c) If $m_1<T<2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T-m<\displaystyle \frac{T}{2}<m$ and $m-\displaystyle \frac{T}{2}=\displaystyle \frac{T}{2}-(T-m),$ then $t_1^*=m\,\,\text {or}\,\,T-m.$

• Case 2 If $p\ge c(1+m)+km+hm(1+m),$ then $\frac{(p-c)(1+m)}{p+k+h(1+m)}\ge m$ and $m_1\ge 2m.$ Hence $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0$ as $T\in (0,2m),$ and ${\varPi }_2$ is a concave function of $t_1.$ Set $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}=0$, it yields $t_1^*=\displaystyle \frac{T}{2}.$

The proof is completed.

1.3 Proof of Proposition 3

Suppose that $c>b.$ Denote

$$\begin{aligned} m_{21}= & {} \displaystyle \frac{A-B}{2(p+k+h(1+m))},\\ m_{22}= & {} m+\displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)},\\ m_{23}= & {} \displaystyle \frac{A+B}{2(p+k+h(1+m))},\\ m_{24}= & {} m+\displaystyle \frac{(p-\frac{(c+b)}{2})(1+m)}{p+k+h(1+m)},\\ m_{25}= & {} m+\displaystyle \frac{(p-b)(1+m)}{p+k+h(1+m)}, \end{aligned}$$

where

$$\begin{aligned} A=(1+2m)(p+k)-(b+k)(1+m)+hm(1+m) \end{aligned}$$

and

$$\begin{aligned} B=\sqrt{A^2-4(p+k+h(1+m))(c-b)(1+m)m}. \end{aligned}$$

Based on Eq. (14), we have

$$\begin{aligned} \displaystyle \frac{\partial {\varPi }_2}{\partial t_1}= & {} \displaystyle \frac{D[p+k+h(1+m)]}{m(1+m)}\left[ 2(T-m_{24})t_1-(T-m_{21})(T-m_{23})\right] \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{\partial ^2 {\varPi }_2}{\partial t_1^2}= & {} \displaystyle \frac{2D[p+k+h(1+m)]}{m(1+m)}(T-m_{24}). \end{aligned}$$

Set $\displaystyle \frac{\partial {\varPi }_2}{\partial t_1}=0$ and we have

$$\begin{aligned} T_{2c}= & {} \displaystyle \frac{(T-m_{21})(T-m_{23})}{2(T-m_{24})}=\displaystyle \frac{T}{2}+\displaystyle \frac{(c-b)(1+m)(m-\frac{T}{2})}{2(T-m_{24})(p+k+h(1+m))}. \end{aligned}$$

Then it has

$$\begin{aligned} (T-T_{2c})-m= & {} \displaystyle \frac{(T-2m)(T-m_{22})}{2(T-m_{24})}\\ T_{2c}-m= & {} \displaystyle \frac{(T-2m)(T-m_{25})}{2(T-m_{24})}\\ T-T_{2c}= & {} \displaystyle \frac{T^2-m_{22}T-m_{21}m_{23}}{2(T-m_{24})}. \end{aligned}$$

• Case 1 If $p<b(1+m)+km+h(1+m),$ it can be proved that

  $$\begin{aligned} 0<m_{21}<m<m_{22}<m_{23}<m_{24}<m_{25}<2m. \end{aligned}$$

  • (a) If $0<T\le m_{21},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}\le 0,$ we have $t_1^*=0.$

  • (b) If $m_{21}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{22},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{22}<T\le m_{23},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T-m,$ we have $t_1^*=T-m.$

  • (e) If $m_{23}<T< m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}< T-m,$ we have $t_1^*=T-m.$

  • (f) If $T= m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}=0,$ and $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}<0.$ Since it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=T-m.$

  • (g) If $m_{24}<T\le m_{25},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $m<T_{2c},$ we have $t_1^*=T-m.$

  • (h) If $m_{25}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ It shows that $\frac{T}{2}<T_{2c}$ and $T-m<T_{2c}<m.$ Since $m-T_{2c}-T_{2c}-(T-m))=T-2T_{2c}<0,$ we have $t_1^*=T-m.$

  Therefore, we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} 0, &{} T\in (0,m_{21}] \\ T_{2c},&{} T\in (m_{21},m_{22}] \\ T-m,&{}T\in (m_{22},2m) \end{array} \right. \end{aligned}$$

• Case 2 If $b(1+m)+km+hm(1+m)\le p<\frac{c+b}{2}(1+m)+km+hm(1+m),$ it can be proved that

  $$\begin{aligned} 0<m_{21}<m<m_{22}<m_{23}<m_{24}<2m<m_{25}. \end{aligned}$$

  • (a) If $0<T\le m_{21},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}\le 0,$ we have $t_1^*=0.$

  • (b) If $m_{21}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{22},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{22}<T\le m_{23},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T-m,$ we have $t_1^*=T-m.$

  • (e) If $m_{23}<T< m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}< T-m,$ we have $t_1^*=T-m.$

  • (f) If $T= m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}=0,$ and $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}<0.$ Since it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=T-m.$

  • (g) If $m_{24}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T_{2c}>m,$ we have $t_1^*=T-m.$

  Then we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} 0, &{} T\in (0,m_{21}] \\ T_{2c},&{} T\in (m_{21},m_{22}] \\ T-m,&{}T\in (m_{22},2m) \end{array} \right. \end{aligned}$$

• Case 3 If $\frac{c+b}{2}(1+m)+km+hm(1+m)\le p<c(1+m)+km+hm(1+m),$ it can be proved that

  $$\begin{aligned} 0<m_{21}<m<m_{22}<2m<m_{24}<m_{23}<m_{25}. \end{aligned}$$

  • (a) If $0<T\le m_{21},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}\le 0$ and it requires that $0\le t_1\le T$, we have $t_1^*=0.$

  • (b) If $m_{21}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{22},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{22}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T-m,$ we have $t_1^*=T-m.$

  Then we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} 0, &{} T\in (0,m_{21}] \\ T_{2c},&{} T\in (m_{21},m_{22}] \\ T-m,&{}T\in (m_{22},2m) \end{array} \right. \end{aligned}$$

• Case 4 If $c(1+m)+km+hm(1+m)\le p,$ it can be proved that

  $$\begin{aligned} 0<m_{21}<m<2m<m_{22}<m_{24}<m_{23}<m_{25}. \end{aligned}$$

  • (a) If $0<T\le m_{21},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T_{2c}\le 0$ and it requires that $0\le t_1\le T$, we have $t_1^*=0.$

  • (b) If $m_{21}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T/2,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  Then we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} 0, &{} T\in (0,m_{21}] \\ T_{2c},&{} T\in (m_{21},2m) \end{array} \right. \end{aligned}$$

It shows that the results in Cases 1, 2 and 3 are the same, hence if $p<c(1+m)+km+hm(1+m),$

$$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} 0, &{} T\in (0,m_{21}] \\ T_{2c},&{} T\in (m_{21},m_{22}] \\ T-m,&{}T\in (m_{22},2m) \end{array} \right. . \end{aligned}$$

The proof is completed.

1.4 Proof of Proposition 4

Suppose that $c<b.$ Denote

$$\begin{aligned} m_{21}= & {} \displaystyle \frac{A-B}{2(p+k+h(1+m))},\\ m_{22}= & {} m+\displaystyle \frac{(p-c)(1+m)}{p+k+h(1+m)},\\ m_{23}= & {} \displaystyle \frac{A+B}{2(p+k+h(1+m))},\\ m_{24}= & {} m+\displaystyle \frac{(p-\frac{(c+b)}{2})(1+m)}{p+k+h(1+m)},\\ m_{25}= & {} m+\displaystyle \frac{(p-b)(1+m)}{p+k+h(1+m)},\\ m_{31}= & {} \displaystyle \frac{E-F}{2(p+k+h(1+m))},\\ m_{36}= & {} \displaystyle \frac{E+F}{2(p+k+h(1+m))},\\ T_{2c}= & {} \displaystyle \frac{(T-m_{21})(T-m_{23})}{2(T-m_{24})}, \end{aligned}$$

where

$$\begin{aligned} A=[p+k+h(1+m)]m+(p-b)(1+m), \\B=\sqrt{A^2-4(p+k+h(1+m))(c-b)(1+m)m}, \\E=[p+k+h(1+m)]m+(p-c)(1+m) \end{aligned}$$

and

$$\begin{aligned} F=\sqrt{E^2-4(p+k+h(1+m))(b-c)(1+m)m}. \end{aligned}$$

Based on Eq. (14), we have

$$\begin{aligned} \displaystyle \frac{\partial {\varPi }_2}{\partial t_1}= & {} \displaystyle \frac{D[p+k+h(1+m)]}{m(1+m)}\left[ 2(T-m_{24})t_1-(T-m_{21})(T-m_{23})\right] \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{\partial ^2 {\varPi }_2}{\partial t_1^2}= & {} \displaystyle \frac{2D[p+k+h(1+m)]}{m(1+m)}(T-m_{24}). \end{aligned}$$

Set $\displaystyle \frac{\partial {\varPi }_2}{\partial t_1}=0$ and we have

$$\begin{aligned} T_{2c}= & {} \displaystyle \frac{(T-m_{21})(T-m_{23})}{2(T-m_{24})}=\displaystyle \frac{T}{2}+\displaystyle \frac{(c-b)(1+m)(m-\frac{T}{2})}{2(T-m_{24})(p+k+h(1+m))}. \end{aligned}$$

Then it has

$$\begin{aligned} (T-T_{2c})-m= & {} \displaystyle \frac{(T-2m)(T-m_{22})}{2(T-m_{24})}\\ T_{2c}-m= & {} \displaystyle \frac{(T-2m)(T-m_{25})}{2(T-m_{24})}\\ T-T_{2c}= & {} \displaystyle \frac{T^2-m_{22}T-m_{21}m_{23}}{2(T-m_{24})}. \end{aligned}$$

• Case 1 If $p<c(1+m)+km+h(1+m),$ it can be proved that

  $$\begin{aligned} m_{21}<0<m_{31}<m<m_{25}<m_{24}<m_{23}<m_{22}<2m. \end{aligned}$$

  • (a) If $0<T\le m_{31},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T<T_{2c},$ we have $t_1^*=T.$

  • (b) If $m_{31}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{25},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{25}<T< m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $m<T_{2c},$ we have $t_1^*=m.$

  • (e) If $T= m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}=0,$ and $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}>0.$ Since it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=m.$

  • (f) If $m_{24}<T\le m_{23},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T_{2c}<0$ and it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=m.$

  • (g) If $m_{23}<T\le m_{22},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T_{2c}<T-m,$ we have $t_1^*=m.$

  • (h) If $m_{22}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T-m<T_{2c}<m$ and $T_{2c}<T/2,$ we have $t_1^*=m.$

  Therefore, we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} T, &{} T\in (0,m_{31}] \\ T_{2c},&{} T\in (m_{31},m_{25}] \\ m,&{}T\in (m_{25},2m) \end{array} \right. \end{aligned}$$

• Case 2 If $c(1+m)+km+hm(1+m)\le p<\frac{c+b}{2}(1+m)+km+hm(1+m),$ it can be proved that

  $$\begin{aligned} m_{21}<0<m_{31}<m<m_{25}<m_{24}<m_{23}<2m<m_{22}. \end{aligned}$$

  • (a) If $0<T\le m_{31},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T<T_{2c}<m,$ we have $t_1^*=T.$

  • (b) If $m_{31}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{25},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{25}<T< m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $m<T_{2c},$ we have $t_1^*=m.$

  • (e) If $T= m_{24},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}=0,$ and $\displaystyle \frac{\partial {{\varPi }_2}}{\partial {t_1}}>0.$ Since it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=m.$

  • (f) If $m_{24}<T\le m_{23},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $T_{2c}<0<T-m<m,$ we have $t_1^*=m.$

  • (g) If $m_{23}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}>0,$ and ${\varPi }_2$ is a convex function of $t_1.$ Since $0<T_{2c}<T-m$ and it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=m.$

  Therefore, we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} T, &{} T\in (0,m_{31}] \\ T_{2c},&{} T\in (m_{31},m_{25}] \\ m,&{}T\in (m_{25},2m) \end{array} \right. \end{aligned}$$

• Case 3 If $\frac{c+b}{2}(1+m)+km+hm(1+m)\le p<b(1+m)+km+hm(1+m),$ it can be proved that

  $$\begin{aligned} m_{21}<0<m_{31}<m<m_{25}<2m<m_{23}<m_{24}<m_{22}. \end{aligned}$$

  • (a) If $0<T\le m_{31},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T<T_{2c},$ we have $t_1^*=T.$

  • (b) If $m_{31}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T\le m_{25},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m,$ we have $t_1^*=T_{2c}.$

  • (d) If $m_{25}<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $m<T_{2c}$ and it requires that $T-m\le t_{1}\le m,$ we have $t_1^*=m.$

  Therefore, we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} T, &{} T\in (0,m_{31}] \\ T_{2c},&{} T\in (m_{31},m_{25}] \\ m,&{}T\in (m_{25},2m) \end{array} \right. \end{aligned}$$

• Case 4 If $b(1+m)+km+hm(1+m)\le p,$ it can be proved that

  $$\begin{aligned} m_{21}<0<m_{31}<m<2m<m_{25}<m_{23}<m_{24}<m_{22}. \end{aligned}$$

  • (a) If $0<T\le m_{31},$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T<T_{2c}$ and it requires that $0\le t_1\le T,$ we have $t_1^*=T.$

  • (b) If $m_{31}<T\le m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $0<T_{2c}<T$ and it requires that $0\le t_1\le T,$ we have $t_1^*=T_{2c}.$

  • (c) If $m<T< 2m,$ then $\displaystyle \frac{\partial ^2{{\varPi }_2}}{\partial {t_1}^2}<0,$ and ${\varPi }_2$ is a concave function of $t_1.$ Since $T-m<T_{2c}<m$ and it requires that $T-m \le t_1\le T,$ we have $t_1^*=T_{2c}.$

  Therefore, we have

  $$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} T, &{} T\in (0,m_{31}] \\ T_{2c},&{} T\in (m_{31},2m) \end{array} \right. \end{aligned}$$

It shows that the results in Cases 1, 2 and 3 are the same, hence if $p<b(1+m)+km+hm(1+m),$

$$\begin{aligned} t_1^*=\left\{ \begin{array}{ccc} T, &{} T\in (0,m_{31}] \\ T_{2c},&{} T\in (m_{31},m_{25}] \\ m,&{}T\in (m_{25},2m) \end{array} \right. \end{aligned}$$

The proof is completed.

1.5 Proof of Lemma 1

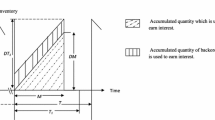
Denote $T_s=T-\tau .$The total number of items sold during the time period $[\tau , T]$ is

$$\begin{aligned} Q_{\tau T}=\int _{\tau }^{T}\lambda (t)dt=\int _{0}^{T-\tau }\lambda _1(t)dt=D(1-\displaystyle \frac{\tau }{m})T_s-D\displaystyle \frac{T_s^2}{2m}. \end{aligned}$$

Since $0\le T_s\le m-\tau$ and $\displaystyle \frac{\partial Q_{\tau T}}{T_s}>0,$ it implies that $Q_{\tau T}$ increases as $T_s$ increases. Hence

$$\begin{aligned} \max _{T_s\in [0,m-\tau ]}Q_{\tau T}=Q_{\tau T}(T_s=m-\tau )=D\displaystyle \frac{(m-\tau )^2}{2m}=M_Q \end{aligned}$$

Then if $Q_{I\tau }\ge M_Q,$ $T_s^*=m-\tau$ and $T^*=m;$

If $Q_{I\tau }< M_Q,$ we have

$$\begin{aligned} Q_{I\tau }=D(1-\displaystyle \frac{\tau }{m})T_s-D\displaystyle \frac{T_s^2}{2m}. \end{aligned}$$

Then $T_s^*=m-\tau -\sqrt{(m-\tau )^2-2\frac{m}{D}Q_{I\tau }},$ and $T^*=m-\sqrt{(m-\tau )^2-2\frac{m}{D}Q_{I\tau }}.$

1.6 Proof of Lemma 2

Based on lemma 1, if $Q_{I\tau }> M_Q,$ the inventory holder can increase the profit by decrease the quantity of Q. Therefore it has

$$\begin{aligned} Q_{I\tau }\le M_Q, \end{aligned}$$

that is

$$\begin{aligned} \displaystyle \frac{1+m-\tau }{1+m}(Q-D\tau +D\displaystyle \frac{\tau ^2}{2m})\le D\displaystyle \frac{(m-\tau )^2}{2m}. \end{aligned}$$

Then

$$\begin{aligned} Q\le V \end{aligned}$$

where

$$\begin{aligned}&V=D\displaystyle \frac{1+m}{2m}\displaystyle \frac{(m-\tau )^2}{1+m-\tau }+D\tau -D\displaystyle \frac{\tau ^2}{2m}. \\&\displaystyle \frac{\partial V}{\partial \tau }=D\displaystyle \frac{m-\tau }{m(1+m-\tau )^2}(\tau -v_1)(\tau -v_2), \end{aligned}$$

where $v_1=\displaystyle \frac{3(1+m)-\sqrt{(1+m)^2+8(1+m)}}{4}$ and $v_1=\displaystyle \frac{3(1+m)+\sqrt{(1+m)^2+8(1+m)}}{4}.$

$$\begin{aligned} \displaystyle \frac{\partial ^2 V}{\partial \tau ^2}=\displaystyle \frac{D}{m}\left[ \displaystyle \frac{1+m}{(1+m-\tau )^3}-1\right] , \end{aligned}$$

V is concave in $[0,1+m-(1+m)^{1/3})$ and convex in $[1+m-(1+m)^{1/3}, m).$ Since

$$\begin{aligned} v_1<1+m-(1+m)^{1/3}<m<v_2, \end{aligned}$$

V reaches its maximum at $\tau =v_1.$ Hence $Q\le V(\tau =v_1).$ The proof is completed.

1.7 Proof of Lemma 4

If the serviceable items are sold out before time m,  it has

$$\begin{aligned} Q=\displaystyle \frac{1+m}{m}(Dt+D\ln (1+m-t)-D\ln (1+m)). \end{aligned}$$

Denote $D_t= \displaystyle \frac{1+m}{m}(Dt+D\ln (1+m-t)-D\ln (1+m)),$ then

$$\begin{aligned} \displaystyle \frac{\partial D_t}{\partial t}=D\displaystyle \frac{1+m}{m}\bigg (1-\displaystyle \frac{1}{1+m-t})\bigg >0. \end{aligned}$$

Hencex

$$\begin{aligned} \max _{t\in [0,m]}D_t=D(1+m)-\displaystyle \frac{1+m}{m}\ln (1+m)), \end{aligned}$$

and

$$\begin{aligned} Q\le \max _{t\in [0,m]}D_t. \end{aligned}$$

The proof is completed.

1.8 Proof of Proposition 5

Based on Eq. (27), we have

$$\begin{aligned} \displaystyle \frac{Q}{T}= & {} D\displaystyle \frac{1+m}{m}\bigg (1+\displaystyle \frac{1}{T}\ln \displaystyle \frac{1+m-T}{1+m}\bigg )\le D\displaystyle \frac{1+m}{m}\bigg (1+\ln \displaystyle \frac{m}{1+m}\bigg ) <D. \end{aligned}$$

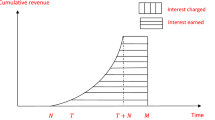
Then the average cost of one product is

$$\begin{aligned} \displaystyle \frac{TC_4}{Q}=c+d+g\displaystyle \frac{T}{Q}>c+d+\displaystyle \frac{g}{D}. \end{aligned}$$

Therefore, we suppose that the sales price is greater than $c+d+g/D.$

$$\begin{aligned} {\varPi }_4= & {} TR-TC\nonumber \\= & {} PDT-PD\displaystyle \frac{T^2}{2m}\nonumber \\&-\displaystyle \frac{(c+d)(1+m)}{m}\left[ DT+D\ln (1+m-T)-D\ln (1+m)\right] -gT. \end{aligned}$$

We have

$$\begin{aligned} \displaystyle \frac{\partial {\varPi } _4}{\partial T}= & {} \displaystyle \frac{1}{m}\left[ pDm-pDT-(c+d)(1+m)D\left( 1-\displaystyle \frac{1}{1+m-T}\right) -gm\right] \\= & {} \displaystyle \frac{1}{my}\left\{ pDy^2-[pD+(c+d)(1+m)D+gm]y+(c+d)(1+m)D\right\} , \end{aligned}$$

where $y=1+m-T.$

$$\begin{aligned} \displaystyle \frac{\partial ^2 {\varPi } _4}{\partial T^2}= & {} -\displaystyle \frac{D}{m}\left[ p-(c+d)(1+m)\displaystyle \frac{1}{(1+m-T)^2}\right] . \end{aligned}$$

Denote

$$\begin{aligned} t_d=1+m-\sqrt{\displaystyle \frac{c+d}{p}(1+m)}, \end{aligned}$$

then $\displaystyle \frac{\partial ^2 {\varPi } _4}{\partial T^2}<0$ when $T\in (0,t_d),$ $\displaystyle \frac{\partial ^2 {\varPi } _4}{\partial T^2}=0$ when $T=t_d,$ $\displaystyle \frac{\partial ^2 {\varPi } _4}{\partial T^2}>0$ when $T\in (t_d,m),$ which implies that ${\varPi } _4$ is concave in $(0,t_d)$ and convex in $(t_d,m).$

Denote

$$\begin{aligned} G= & {} pD+(c+d)(1+m)D+mg,\\ H= & {} 4pD(c+d)(1+m)D.\\ \end{aligned}$$

Set $\displaystyle \frac{\partial {\varPi } _4}{\partial T}=0,$ then $y_1=\displaystyle \frac{G+\sqrt{G^2-H}}{2pD}$ and $y_2=\displaystyle \frac{G-\sqrt{G^2-H}}{2pD}$. $T_{y1}=1+m-y_1$ and $T_{y2}=1+m-y_2.$ It can be proved that $1<y_1<m+1$ when $c+d+g/D<p.$ It also has $y_2<1.$

• (a) If $c+d+g/D<p<(c+d)(1+m),$ then $0<t_d<m$ and it can be proved that $0<T_{y1}<t_d<m<T_{y2}.$ Then the optimal replenishment cycle is $T^*=1+m-y_1.$

• (b) If $(c+d)(1+m)\le p,$ then $m\le t_d.$ It can be proved that $0<T_{y1}<m<t_d$ and $m<T_{y2}.$ Then the optimal replenishment cycle is $T^*=1+m-y_1.$

Therefore the optimal replenishment cycle is $T^*=1+m-y_1$ as $c+d+g/D<p$, and the optimal quantity is

$$\begin{aligned} Q^*=\displaystyle \frac{1+m}{m}(DT^*+D\ln (1+m-T^*)-D\ln (1+m)). \end{aligned}$$

The proof is completed.