Propagation of surface waves past asymmetric elastic plates

Abstract

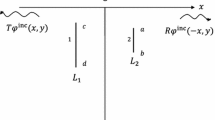
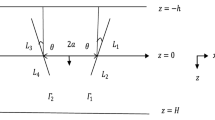
Water wave scattering by two asymmetric thin elastic plates with arbitrary inclinations is investigated using integral equations. The plates are submerged in finite depth water. The assumption of Euler–Bernoulli beam model for the plates, the use of the appropriate Euclidean transformations to handle the fifth-order plate conditions and the application of Green’s function technique allow us to obtain the expressions of normal velocities at arbitrary points over the plates. On the other hand, an application of Green’s integral theorem on the scattered potential and the source potential functions gives us the alternative expressions of the above-mentioned normal velocities. The comparison of these alternative forms provides two coupled integral equations involving the unknown potential differences across the plates. Kernels of the integral equations have regular as well as hypersingular parts so that the resulting integral equations are hypersingular in nature. These are solved numerically and the solutions are utilized to compute the numerical estimates for different physical quantities. Published results are recovered for different arrangements of the plates and new results are presented graphically for various parametric values.

Appendix A: Determination of the expressions of \(g_i(Y_i,\overline{Y_i})\)

Here we discuss the process of determining the Green’s functions satisfying the boundary value problems given by equations (15) and end conditions (14). Other inherent conditions to be satisfied by these Green’s functions are given as

$$\begin{aligned} g_{i}, \frac{\partial g_{i}}{\partial {Y_i}}, \frac{\partial ^2 g_i}{\partial {Y_i}^2} \quad ~\text{ to } \text{ be } \text{ continuous } \text{ at }~ {Y_i} = \overline{Y_i}, \end{aligned}$$

(A.1)

and

$$\begin{aligned} \Bigg (\frac{\partial ^3 g_i}{\partial {Y_i}^3}\Bigg )_{{Y_i}=\overline{Y_i}+0} - \Bigg (\frac{\partial ^3 g_i}{\partial {Y_i}^3}\Bigg )_{{Y_i}=\overline{Y_i}-0} = -1. \end{aligned}$$

(A.2)

The general solutions of Eq. (15) (for $i=1,2$) are of the form

$$\begin{aligned} g_i(Y_i,\overline{Y_i})= \left\{ \begin{array}{lcl} \displaystyle A_{i1}\mathrm {e}^{\mathrm {i}\lambda _i {Y_i}}+B_{i1}\mathrm {e}^{-\mathrm {i}\lambda _i {Y_i}}+C_{i1}\mathrm {e}^{\lambda _i {Y_i}}+D_{i1}\mathrm {e}^{-\lambda _i {Y_i}}, ~-b_i< {Y_i}< \overline{Y_i}<b_i, \\ \displaystyle A_{i2}\mathrm {e}^{\mathrm {i}\lambda _i {Y_i}}+B_{i2}\mathrm {e}^{-\mathrm {i}\lambda _i {Y_i}}+C_{i2}\mathrm {e}^{\lambda _i {Y}}+D_{i2}\mathrm {e}^{-\lambda _i {Y_i}}, ~-b_i< \overline{Y_i}< {Y_i}< b_i, \end{array} \right. \end{aligned}$$

(A.3)

where $A_{i1},B_{i1}\ldots$ are to be determined. Using end conditions (14) and the inherent properties of the Green’s functions we get the system of equations

$$\begin{aligned} {\mathcal {U}}_{i}{\mathcal {V}}_{i}={\mathcal {W}}_{i}, \quad i=1,2. \end{aligned}$$

(A.4)

Here

$$\begin{aligned} {\mathcal {U}}_{i}= & {} \left[ \begin{array}{l} A_{1i}\\ B_{1i}\\ C_{1i}\\ D_{1i} \end{array}\right] ,\quad {\mathcal {V}}_{i}=\left[ \begin{array}{cccc} \mathrm {e}^{-\mathrm {i}\lambda _i b_i} &{} \mathrm {e}^{\mathrm {i}\lambda _i b_i} &{} \mathrm {e}^{-\lambda _i b_i} &{} \mathrm {e}^{\lambda _i b_i}\\ \mathrm {i}\mathrm {e}^{-\mathrm {i}\lambda _i b_i} &{} -\mathrm {i}\mathrm {e}^{\mathrm {i}\lambda _i b_i} &{} \mathrm {e}^{-\lambda _i b_i} &{} -\mathrm {e}^{\lambda _i b_i}\\ -\mathrm {e}^{\mathrm {i}\lambda _i b_i} &{} -\mathrm {e}^{-\mathrm {i}\lambda _i b_i} &{} \mathrm {e}^{\lambda _i b_i} &{} \mathrm {e}^{-\lambda _i b_i}\\ -(\mathrm {i}\lambda _i^{3}+M_{u_{i}}) \mathrm {e}^{\mathrm {i}\lambda _i b_i} &{} (\mathrm {i}\lambda _i^{3}-M_{u_{i}})\mathrm {e}^{-\mathrm {i}\lambda _i b_i} &{} (\lambda _i^{3}-M_{u_{i}})\mathrm {e}^{\lambda _i b_i} &{} -(\lambda _i^{3}+M_{u_{i}})\mathrm {e}^{-\lambda _i b_i} \end{array} \right] , \\ {\mathcal {W}}_{i}= & {} \frac{1}{4\lambda _i^3} \left[ \begin{array}{c} 0\\ 0\\ -\mathrm {i}\mathrm {e}^{\mathrm {i}\lambda _i \gamma _i}+\mathrm {i}\mathrm {e}^{-\mathrm {i}\lambda _i \gamma _i}+\mathrm {e}^{\lambda _i \gamma _i}-\mathrm {e}^{-\lambda _i \gamma _i}\\ -\mathrm {i}(\mathrm {i}\lambda _i^{3}+M_{u_{i}})\mathrm {e}^{\mathrm {i}\lambda _i \gamma _i}-\mathrm {i}(\mathrm {i}\lambda _i^{3}-M_{u_{i}})\mathrm {e}^{-\mathrm {i}\lambda _i \gamma _i}+(\lambda _i^{3}-M_{u_{i}})\mathrm {e}^{\lambda _i \gamma _i}+(\lambda _i^{3}+M_{u_{i}})\mathrm {e}^{-\lambda _i \gamma _i} \end{array} \right] , \end{aligned}$$

where $\gamma _i=b_i-\overline{Y_i}$. Also, the values of $A_{2i},B_{2i},C_{2i},D_{2i}$ are found by the relations

$$\begin{aligned} A_{2i}=A_{1i}-\frac{\mathrm {i}}{4\lambda _i^3}\mathrm {e}^{-\mathrm {i}\lambda _i \overline{Y_i}},~ B_{2i}=B_{1i}+\frac{\mathrm {i}}{4\lambda _i^3}\mathrm {e}^{\mathrm {i}\lambda _i \overline{Y_i}},~ C_{2i}=C_{1i}-\frac{1}{4\lambda _i^3}\mathrm {e}^{-\lambda _i \overline{Y_i}},~ D_{2i}=D_{1i}+\frac{1}{4\lambda _i^3}\mathrm {e}^{\lambda _i \overline{Y_i}}. \end{aligned}$$

(A.5)