Quantum autoencoders for communication-efficient cloud computing

Abstract

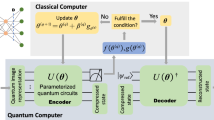
In the model of quantum cloud computing, the server executes a computation on the quantum data provided by the client. In this scenario, it is important to reduce the amount of quantum communication between the client and the server. A possible approach is to transform the desired computation into a compressed version that acts on a smaller number of qubits, thereby reducing the amount of data exchanged between the client and the server. Here we propose quantum autoencoders for quantum gates (QAEGate) as a method for compressing quantum computations. We illustrate it in concrete scenarios of single-round and multi-round communication and validate it through numerical experiments. A bonus of our method is it does not reveal any information about the server’s computation other than the information present in the output.

Appendix

1.1 A. Proof of Theorem 1

According to Allen-Zhu (2017), we have the following lemma about convergence of SGD for nonconvex functions:

Lemma 1

If a function f(x) is $L_1$-smooth and we perform SGD update $x_{t+1}\leftarrow x_t - \eta \nabla f_i(x_t)$ each time for a random $i\in [n]$, then the convergence rate is $T = \mathcal {O}(\frac{L_1}{\epsilon ^4})$ for finding $\mathbb {E}[\Vert \nabla f(x) \Vert ^2]\le \epsilon ^2$.

Therefore, we first discuss the smoothness property of the loss function $\mathcal {L}(\varvec{\theta })$ in the training of QAEGate model. Note that the first- and second-order Lipschitz smoothness are equivalent to Lipschitz continuity of the first- and second-order derivatives. So we start with a lemma about the Lipschitz continuity of multivariate functions (Sweke et al. 2020).

Lemma 2

Given some function $f :\textbf{R}^M \rightarrow \textbf{R}$, if all partial derivatives of f are continuous, then for any $a, b \in \textbf{R}$ the function $f :[a, b]^M \rightarrow \textbf{R}$ is L-Lipschitz continuous with

$$\begin{aligned} L = \sqrt{M}\underset{j \in \{1,\dots ,M\}}{\textrm{max}} \sup _{\varvec{x}\in [a, b]^M} \left| \frac{\partial f(\varvec{x})}{\partial x_j}\right| . \end{aligned}$$

(3)

Next we prove a more general result about the smoothness of measurement probability of quantum circuits, and then show that $\mathcal {L}(\varvec{\theta })$ fits into this result.

Lemma 3

Consider a quantum circuit consisting of any number of fixed unitary gates and M variable unitary gates $U_1(\theta _1),\dots ,U_M(\theta _M)$, where $U_j(\theta _j):= \textrm{exp}(i\theta _j H_j)$ for some Hermitian operator $H_j$. Then the probability of any measurement outcome of the output of this circuit is $L_1$-smooth and $L_2$-second-order smooth with respect to $\varvec{\theta }=(\theta _1,\dots ,\theta _M)$, where

$$\begin{aligned} L_1= & {} 4MH_{\textrm{max}}^2\end{aligned}$$

(4)

$$\begin{aligned} L_2= & {} 8M^{3/2}H_{\textrm{max}}^3 \end{aligned}$$

(5)

where $H_{\textrm{max}}:=\textrm{max}_{j} \Vert H_j\Vert _2$ and $\Vert \cdot \Vert _2$ is the induced operator norm defined as $\Vert A\Vert _2:= \sup \frac{\Vert Ax\Vert _2}{\Vert x\Vert _2}$.

Proof

Let $\vert \psi _0\rangle$ be the initial state of the circuit. Without loss of generality, we assume the variable unitary gates are labeled as $U_1(\theta _1)$ to $U_M(\theta _M)$ according to the order they are applied. Then the output of this circuit can be written as $\vert \psi _{\varvec{\theta }}\rangle := V_M U_M(\theta _M) \dots V_1 U_1(\theta _1) V_0 \vert \psi _0\rangle$, where $V_1,\dots ,V_M$ denotes the fixed unitary gates. A measurement outcome can be described by a positive operator-valued measure (POVM) element P with the property that P and $I-P$ are both positive semidefinite, where I is the identity operator of the output. The probability of this outcome is

$$\begin{aligned} f(\varvec{\theta }):= \textrm{Tr}[P \vert \psi _{\varvec{\theta }}\rangle \langle \psi _{\varvec{\theta }}\vert ] = \langle \psi _{\varvec{\theta }}\vert P \vert \psi _{\varvec{\theta }}\rangle . \end{aligned}$$

(6)

To study the smoothness of $f(\varvec{\theta })$, we take the partial derivatives:

$$\begin{aligned} \frac{\partial f(\varvec{\theta })}{\partial \theta _j}= & {} \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \vert \psi _{\varvec{\theta }}\rangle + \langle \psi _{\varvec{\theta }}\vert P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _j}\\= & {} 2 \Re \left( \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \vert \psi _{\varvec{\theta }}\rangle \right) \\ \frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}= & {} 2 \Re \left( \frac{\partial ^2\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k} P \vert \psi _{\varvec{\theta }}\rangle + \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k} \right) \\ \frac{\partial ^3 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k \partial \theta _l}= & {} 2 \Re \left( \frac{\partial ^3\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k \partial \theta _l} P \vert \psi _{\varvec{\theta }}\rangle +\frac{\partial ^2\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _l}\right. \\{} & {} \left. + \frac{\partial ^2 \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _l} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k} + \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \frac{\partial ^2\vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k \partial \theta _l} \right) \end{aligned}$$

These partial derivatives can be bounded with vector and operator norms. For a unitary operator U, $\Vert U\Vert _2=1$. For the POVM element P, $\Vert P\Vert _2\le 1$. The second-order partial derivatives can be bounded as:

$$\begin{aligned} \left| \frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}\right|\le & {} 2 \left| \frac{\partial ^2\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k} P \vert \psi _{\varvec{\theta }}\rangle + \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k} \right| \nonumber \\\le & {} 2\left\| \frac{\partial ^2\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k}\right\| _2 \Vert P\Vert _2 \Vert \vert \psi _{\varvec{\theta }}\rangle \Vert _2 + 2\left\| \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j}\right\| _2\nonumber \\{} & {} \times \Vert P\Vert _2 \left\| \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k}\right\| _2 \nonumber \\\le & {} 2\underset{a,b}{\textrm{max}}\left\| \frac{\partial ^2\vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b}\right\| _2 + 2 \underset{a}{\textrm{max}} \left\| \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a}\right\| _2^2 \end{aligned}$$

(7)

Similarly, for the third-order partial derivatives,

$$\begin{aligned} \left| \frac{\partial ^3 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k \partial \theta _l} \right|\le & {} 2 \left| \frac{\partial ^3\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k \partial \theta _l} P \vert \psi _{\varvec{\theta }}\rangle + \frac{\partial ^2\langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _k} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _l}\right. \nonumber \\{} & {} \left. + \frac{\partial ^2 \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j \partial \theta _l} P \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k} + \frac{\partial \langle \psi _{\varvec{\theta }}\vert }{\partial \theta _j} P \frac{\partial ^2\vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _k \partial \theta _l} \right| \nonumber \\\le & {} \!2\underset{a,b,c}{\textrm{max}}\left\| \frac{\partial ^3 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b \partial \theta _c}\right\| _2 \!+\! 6\! \left( \underset{a,b}{\textrm{max}}\left\| \frac{\partial ^2 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b}\right\| _2 \right) \nonumber \\{} & {} \! \times \!\left( \underset{a}{\textrm{max}}\left\| \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a }\right\| _2 \right) \end{aligned}$$

(8)

Therefore, to show that the second- and third-order partial derivatives are bounded, it suffices to show that $\textrm{max}_{a}\left\| \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a }\right\| _2, \textrm{max}_{a,b}\left\| \frac{\partial ^2 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b}\right\| _2$ and $\textrm{max}_{a,b,c}\left\| \frac{\partial ^3 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b \partial \theta _c}\right\| _2$ are all bounded. We observe that $\frac{\partial U_j(\theta _j)}{\partial j} = \frac{\partial \textrm{exp}(i\theta _j H_j)}{\partial j} = iH_j U_j(\theta _j)$, and we have

$$\begin{aligned} \underset{a}{\textrm{max}}\left\| \frac{\partial \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a }\right\| _2= & {} \underset{a}{\textrm{max}}\left\| V_M U_M(\theta _M)\dots V_a i H_a U_a(\theta _a)\right. \nonumber \\{} & {} \left. \dots U_1(\theta _1)V_0 \vert \psi _0\rangle \right\| _2 \nonumber \\\le & {} \!\underset{a}{\textrm{max}} \left\| V_M U_M(\theta _M)\! \dots \!V_a \right\| _2 \!\Vert H_a\Vert _2 \left\| U_a(\theta _a)\!\right. \nonumber \\{} & {} \left. \dots U_1(\theta _1)V_0 \vert \psi _0\rangle \right\| _2 \nonumber \\= & {} \underset{a}{\textrm{max}} \Vert H_a\Vert _2 = H_{\textrm{max}} \end{aligned}$$

(9)

With similar derivations, we can obtain $\textrm{max}_{a,b}\left\| \frac{\partial ^2 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b}\right\| _2^2 \le H_{\textrm{max}}^2$ and $\textrm{max}_{a,b,c}\left\| \frac{\partial ^3 \vert \psi _{\varvec{\theta }}\rangle }{\partial \theta _a \partial \theta _b \partial \theta _c}\right\| _2 \le H_{\textrm{max}}^3$. According to Eqs. (7) and (8), we obtain

$$\begin{aligned} \left| \frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}\right|\le & {} 4 H_{\textrm{max}}^2 \end{aligned}$$

(10)

$$\begin{aligned} \left| \frac{\partial ^3 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k \partial \theta _l} \right|\le & {} 8 H_{\textrm{max}}^3 \end{aligned}$$

(11)

Consider $\frac{\partial f(\varvec{\theta })}{\partial \theta _j}$ as a function of $\varvec{\theta }$. Since its partial derivatives $\frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}$ are bounded by $4 H_{\textrm{max}}^2$, according to Lemma 2, $\frac{\partial f(\varvec{\theta })}{\partial \theta _j}$ is $L_1'$-continuous with $L_1'=4 \sqrt{M} H_{\textrm{max}}^2$. Then

$$\begin{aligned} \Vert \nabla f(\varvec{\alpha }) - \nabla f(\varvec{\beta }) \Vert _2\le & {} \sqrt{M}\underset{j}{\textrm{max}} \left| \frac{\partial f(\varvec{\alpha })}{\partial \theta _j} - \frac{\partial f(\varvec{\beta })}{\partial \theta _j} \right| \nonumber \\\le & {} \sqrt{M} L_1' \Vert \alpha - \beta \Vert _2 = 4 M H_{\textrm{max}}^2 \Vert \alpha - \beta \Vert _2 \end{aligned}$$

(12)

and therefore f is $L_1$-smooth with $L_1 = 4 M H_{\textrm{max}}^2$. Similarly, consider $\frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}$ as a function of $\varvec{\theta }$. Since its partial derivatives $\frac{\partial ^3 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k \partial \theta _l}$ are bounded by $8 H_{\textrm{max}}^3$, according to Lemma 2, $\frac{\partial ^2 f(\varvec{\theta })}{\partial \theta _j \partial \theta _k}$ is $L_2'$-continuous with $L_2'=8\sqrt{M} H_{\textrm{max}}^3$. Then

$$\begin{aligned} \Vert \nabla ^2 f(\varvec{\alpha }) - \nabla ^2 f(\varvec{\beta }) \Vert _2\le & {} M \underset{j,k}{\textrm{max}} \left| \frac{\partial ^2 f(\varvec{\alpha })}{\partial \theta _j \partial \theta _k} - \frac{\partial ^2 f(\varvec{\beta })}{\partial \theta _j \partial \theta _k} \right| \nonumber \\\le & {} M L_2' \Vert \alpha \!-\! \beta \Vert _2 \!=\! 8 M^{3/2} H_{\textrm{max}}^3 \Vert \alpha \!-\! \beta \Vert _2 \end{aligned}$$

(13)

and therefore f is $L_2$-second-order smooth with $L_2 = 8 M^{3/2} H_{\textrm{max}}^3$. $\square$

Based on above lemma, we obtain the following theorem:

Theorem 3

(Smoothness) The loss function $\mathcal {L}(\varvec{\theta })$ in the training of QAEGate model is $L_1$-smooth and $L_2$-second-order smooth.

Proof

Let $p(\varvec{\theta })$ be the probability of outcome $\vert +\rangle$ in the SWAP test when the gates are parameterized with $\varvec{\theta =(\theta _{\textrm{le}},\theta _{\textrm{re}},\theta _{\textrm{ld}},\theta _{\textrm{rd}})}$. Because of $\mathcal {L}(\varvec{\theta }) = 1-f(\varvec{\theta })$ and $f(\varvec{\theta }) = 2p(\varvec{\theta })-1$, we just need to discuss the smoothness of $p(\varvec{\theta })$. Since $p(\varvec{\theta })$ is the probability of a measurement outcome of a unitary circuit, and in this circuit, every variable gate has the form of $U_\theta = \textrm{exp}(i\theta H)$, we can apply Lemma 3. Thus, $p(\varvec{\theta })$ is $L_1$-smooth and $L_2$-second-order smooth where $L_1 = 4MH_{\textrm{max}}^2, L_2 = 8M^{3/2}H_{\textrm{max}}^3$ and M is the number of variable gates in the circuit. To prove Theorem 3, we only need to show that $H_{\textrm{max}}$ is bounded.

The variable gates in our circuit only includes the following single- and two-qubit gates:

$$\begin{aligned} R_X(\theta ):= & {} \textrm{exp}(i\theta \sigma _x),\ R_Y(\theta ):= \textrm{exp}(i\theta \sigma _y),\ R_Z(\theta )\nonumber \\{} & {} := \textrm{exp}(i\theta \sigma _z) \end{aligned}$$

(14)

$$\begin{aligned} XX(\theta ):= & {} \textrm{exp}(i\theta \sigma _x\otimes \sigma _x),\ YY(\theta ):=\textrm{exp}(i\theta \sigma _y\otimes \sigma _y),\nonumber \\{} & {} ZZ(\theta ):=\textrm{exp}(i\theta \sigma _z\otimes \sigma _z) \end{aligned}$$

(15)

Therefore, $H_{\textrm{max}} = \textrm{max}\{\Vert \sigma _x\Vert _2,\Vert \sigma _y\Vert _2,\Vert \sigma _z\Vert _2, \Vert \sigma _x\otimes \sigma _x\Vert _2, \Vert \sigma _y\otimes \sigma _y\Vert _2,\Vert \sigma _z\otimes \sigma _z\Vert _2\} = 1$. $\square$

Proof

(Proof of Theorem 1) Based on Theorem 3, we have proved that $\mathcal {L}(\varvec{\theta })$ is $L_1$-smooth, where $L_1 = 4M$. In our implementation, there is only one variable for each variable unitary gate, so $M=\dim {\varvec{\theta }} = \mathcal {O}(n^2)$ here. Then we can apply Lemma 1 and obtain that the convergence rate is $T=\mathcal {O}(\frac{n^2}{\epsilon ^4})$ for finding $\mathbb {E}[\Vert \nabla _{\varvec{\theta }} \mathcal {L}(\varvec{\theta }) \Vert ^2]\le \epsilon ^2$. In order to estimate the gradients, we have to compute the loss function for $\mathcal {O}(\dim {\varvec{\theta }}) = \mathcal {O}(n^2)$ times. The total time complexity of the algorithm is $\mathcal {O}(\frac{n^4}{\epsilon ^4})$. $\square$

1.2 B. Details of numerical experiments

Data generation

For each class of gates U(t) we considered in different scenarios, we randomly generate 60 different $U(t_i), t_i \in [0,2]$ and split them into the training set and the test set with ratio 50 : 10.

Hyperparameters

We set the learning rate $\eta$ as 0.005, the maximum number of iterations K as 150 and the threshold $\delta$ as 0.999 in all experiments.

Impelementation details

We implement our proposed model QAEGate based on Tensorflow Quantum (Broughton et al. 2020). The parameterized quantum circuits are constructed by the tools provided in Cirq (2022) and the gradients are estimated by the differentiators based on parameter shift rule (Mitarai et al. 2018).

Training details

We employed stochastic gradient descent to train all the models in our experiments, using a single GPU. The training time for all the experiments presented in this paper is less than one hour.