Summary
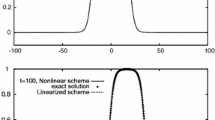
The Lax-Wendroff (L-W) difference scheme for a single conservation law has been shown to be nonlinearly unstable near stagnation points. In this paper a simple variant of L-W is devised which has all the usual properties-conservation form, three point scheme, second order accurate on smooth solutions, but which is shown rigorously to beL 2 stable for Burger's equation and which is believed to be stable in general. This variant is constructed by adding a simple nonlinear viscosity term to the usual L-W operator. The nature of the viscosity is deduced by first stabilizing, for general conservation laws, a model differential equation derived by analyzing the truncation error for L-W, keeping only terms of order (Δt)2. The same procedure is then carried out for an analogous semi-discrete model. Finally, the full L-W difference scheme is rigorously shown to be stable provided that the C.F.L. restriction λ|u j n|≦0.24 is satisfied.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Fornberg, B.: On the instability of leap-frog and Crank-Nicolson approximations of a nonlinear partial differential equation. Math. Comput.27, 45–47 (1973)
Friedel, H., Osher, S.: Nonlinear instability and loss of accuracy for finite difference approximations near shocks and rarefaction waves. Unpublished
Harten, A.: The method of artificial compression: I. Shocks and contact discontinuities. AEC Research and Development Report C00-3077-50, Courant Inst. Math. Sci., New York University, 1974
Harten, A., Hyman, J.M., Lax, P.D.: On finite difference approximations and entropy conditions for shocks. Comm. Pure Appl. Math.29, 297–322 (1976)
Hedstrom, G.: Models of difference schemes foru 1 +u x =0 by partial differential equations. Math. Comput.29, 969–977 (1975)
Kreiss, H.-O., Oliger, J.: Methods for the approximate solution of time dependent problems. Garp Publication Series #10, 1973
Lax, P.D.: Hyperbolic systems of conservation laws and the mathematical theory of shock waves. SIAM Regional Conf. Series. In: Appl. Math., No. 11 (1973)
Lax, P.D.: Shock waves and entropy. Contributions to nonlinear functional analysis (E.H. Zarantonello, ed.), pp. 603–634. New York: Academic Press 1971
Lax, P.D., Wendroff, B.: Systems of conservation laws. Comm. Pure Appl. Math.23, 217–237 (1960)
Lerat, A., Peyret, R.: Sur l'origines des oscillations apparaissant dans les profiles de choc. calculés par des méthodes aux differences. C.R. Acad. Sci. Paris Sér. A276, 759–762 (1973)
Warming, R., Hyett, B.: The modified equation approach to the stability and accuracy analysis of finite-difference methods. J. Computational Phys.14, 159–179 (1974)
Lapidus, A.: A detached shock calculation by second-order finite differences. J. Computational Phys.2, 154–177 (1967)
Author information
Authors and Affiliations
Additional information
Research supported in part by N.S.F. Grants No. MCS 76-10227 and MCS 760-4412
Rights and permissions
About this article
Cite this article
Majda, A., Osher, S. A systematic approach for correcting nonlinear instabilities. Numer. Math. 30, 429–452 (1978). https://doi.org/10.1007/BF01398510
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01398510