PARAFAC-Based Blind Identification of Underdetermined Mixtures Using Gaussian Mixture Model

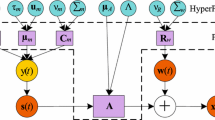
Abstract

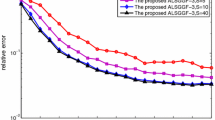
This paper presents a novel algorithm, named GMM-PARAFAC, for blind identification of underdetermined instantaneous linear mixtures. The GMM-PARAFAC algorithm uses Gaussian mixture model (GMM) to model non-Gaussianity of the independent sources. We show that the distribution of the observations can also be modeled by a GMM, and derive a maximum-likelihood function with regard to the mixing matrix by estimating the GMM parameters of the observations via the expectation-maximization algorithm. In order to reduce the computation complexity, the mixing matrix is estimated by maximizing a tight upper bound of the likelihood instead of the log-likelihood itself. The maximum of the tight upper bound is obtained by decomposition of a three-way tensor which is obtained by stacking the covariance matrices of the GMM of the observations. Simulation results validate the superiority of the GMM-PARAFAC algorithm.

Appendix

In this appendix, it is shown that (17) can be formulated as (20).

According to (19)

$$ \mathcal{F}\bigl(\varTheta_{\mathbf{x}},\hat{\varTheta}_{\mathbf{x}}^{*} \bigr) = \frac{1}{T}\sum_{t = 1}^{T} \sum_{m = 1}^{M} \gamma_{t,m}^{*} \log \bigl(\omega_{m}N(\mathbf{x}_{t}|\boldsymbol{ \eta}_{m},\mathbf{R}_{m})\bigr) $$

(31)

where $\gamma_{t,m}^{*} = \hat{\omega}_{m}^{*}N(\mathbf{x}_{t}|\hat{\boldsymbol{\eta }}_{m}^{*},\hat{\mathbf{R}}_{m}^{*}) / \sum_{m' = 1}^{M} \hat{\omega}_{m'}^{*}N(\mathbf{x}_{t}|\hat{\boldsymbol{\eta }}_{m'}^{*},\hat{\mathbf{R}}_{m'}^{*})$. Therefore

$$\begin{aligned} \mathcal{F}\bigl(\varTheta_{\mathbf{x}},\hat{\varTheta}_{\mathbf{x}}^{*} \bigr) &= - \frac{1}{T}\sum_{m = 1}^{M} \Biggl\{ \frac{1}{2}\sum_{t = 1}^{T} \gamma_{t,m}^{*}\log|2\pi\mathbf{R}_{m}| \\ &\quad {}+ \frac{1}{2}\sum_{t = 1}^{T} \gamma_{t,m}^{*}\operatorname{tr} \bigl[\mathbf{R}_{m}^{ - 1}( \mathbf{x}_{t} - \boldsymbol{\eta}_{m}) ( \mathbf{x}_{t} - \boldsymbol{\eta}_{m})^{\operatorname{T}} \bigr] - \sum_{t = 1}^{T} \gamma_{t,m}^{*} \log\omega_{m} \Biggr\} \end{aligned}$$

(32)

Since trace is a linear operator, the summation with regard to t in the mid-term of (32) can be inserted into the trace operator. Hence, (32) can be rewritten in the following form:

$$\begin{aligned} \mathcal{F}\bigl(\varTheta_{\mathbf{x}},\hat{\varTheta}_{\mathbf{x}}^{*} \bigr) &= - \frac{1}{T}\sum_{m = 1}^{M} \Biggl\{ \frac{1}{2}\sum_{t = 1}^{T} \gamma_{t,m}^{*}\log|2\pi\mathbf{R}_{m}| \\ &\quad {}+ \frac{1}{2}\operatorname{tr} \Biggl[\mathbf{R}_{m}^{ - 1} \sum_{t = 1}^{T} \gamma_{t,m}^{*}( \mathbf{x}_{t} - \boldsymbol{\eta}_{m}) ( \mathbf{x}_{t} - \boldsymbol{\eta}_{m})^{\operatorname{T}} \Biggr] - \sum_{t = 1}^{T} \gamma_{t,m}^{*} \log\omega_{m} \Biggr\} \end{aligned}$$

(33)

The factor $\sum_{t = 1}^{T} \gamma_{t,m}^{*}$ can be extracted out of the main brackets and (33) can be formulated as follows:

$$\begin{aligned} \mathcal{F}\bigl(\varTheta_{\mathbf{x}},\hat{\varTheta}_{\mathbf{x}}^{*} \bigr) =& - \frac{1}{T}\sum_{m = 1}^{M} \sum_{t = 1}^{T} \gamma_{t,m}^{*} \biggl\{ \frac{1}{2}\operatorname{tr} \biggl[ \mathbf{R}_{m}^{ - 1} \times \underbrace{\biggl(\frac{\sum_{t = 1}^{T} \gamma_{t,m}^{*}(\mathbf{x}_{t} - \boldsymbol{\eta}_{m})(\mathbf{x}_{t} - \boldsymbol{\eta}_{m})^{\mathrm{T}}}{\sum_{t = 1}^{T} \gamma_{t,m}^{*}} \biggr)}_{\mathbf{G}_{m}} \biggr] \\ &{} + \frac{1}{2}\log|2\pi\mathbf{R}_{m}| - \log \omega_{m} \biggr\} \end{aligned}$$

(34)

The updating equations of the EM algorithm for GMM parameter estimation can be formulated as follows:

$$ \left \{ \begin{array}{l} \hat{\omega}_{m}^{*} = \frac{1}{T}\sum_{t = 1}^{T} \gamma_{t,m}^{*} \\ \hat{\boldsymbol{\eta}}_{m}^{*} = \frac{\sum_{t = 1}^{T} \gamma_{t,m}^{*}\mathbf{x}_{t}}{\sum_{t = 1}^{T} \gamma_{t,m}^{*}} \\ \hat{\mathbf{R}}_{m}^{*} + \hat{\boldsymbol{\eta}}_{m}^{*}(\hat{\boldsymbol{\eta }}_{m}^{*})^{\operatorname{T}} = \frac{\sum_{t = 1}^{T} \gamma_{t,m}^{*}\mathbf{x}_{t}\mathbf{x}_{t}^{\mathrm{T}}}{\sum_{t = 1}^{T} \gamma_{t,m}^{*}} \end{array} \right . $$

(35)

Therefore

$$\begin{aligned} \mathbf{G}_{m} & = \hat{\mathbf{R}}_{m}^{*} + \hat{\boldsymbol{\eta}}_{m}^{*}\bigl(\hat{\boldsymbol{\eta }}_{m}^{*}\bigr)^{\operatorname{T}} - \boldsymbol{ \eta}_{m}\bigl(\hat{\boldsymbol{\eta}}_{m}^{*} \bigr)^{\operatorname{T}} - \hat{\boldsymbol{\eta}}_{m}^{*} \boldsymbol{\eta}_{m}^{\mathrm{T}} + \boldsymbol{\eta}_{m} \boldsymbol{\eta}_{m}^{\mathrm{T}} \\ &= \hat{\mathbf{R}}_{m}^{*} + \bigl(\hat{\boldsymbol{ \eta}}_{m}^{*} - \boldsymbol{\eta}_{m}\bigr) \bigl( \hat{\boldsymbol{\eta}}_{m}^{*} - \boldsymbol{ \eta}_{m}\bigr)^{\operatorname{T}} \end{aligned}$$

(36)

Substitution of (36) into (35), yields the expression (37) as follows:

$$\begin{aligned} & \mathcal{F}\bigl(\varTheta_{\mathbf{x}},\hat{\varTheta}_{\mathbf{x}}^{*} \bigr) \\ &\quad {}= - \sum_{m = 1}^{M} \hat{ \omega}_{m}^{*} \\ &\qquad {}\times \biggl\{ \underbrace{\frac{1}{2} \operatorname{tr} \bigl[\mathbf{R}_{m}^{ - 1}\hat{ \mathbf{R}}_{m}^{*}\bigr] + \frac{1}{2}\bigl(\hat{ \boldsymbol{\eta }}_{m}^{*} - \boldsymbol{ \eta}_{m}\bigr)^{\operatorname{T}} \mathbf{R}_{m}^{ - 1} \bigl(\hat{\boldsymbol{\eta}}_{m}^{*} - \boldsymbol{ \eta}_{m}\bigr) + \frac{1}{2}\log|2\pi\mathbf{R}_{m}| - \log\omega_{m}}_{\mathbf{H}_{m}} \biggr\} \end{aligned}$$

(37)

Applying that η _m =A μ _m and $\mathbf{R}_{m} = \mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}$

$$\begin{aligned} \mathbf{H}_{m} & = \frac{1}{2}\operatorname{tr} \bigl[\bigl( \mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}} \bigr)^{ - 1}\hat{\mathbf{R}}_{m}^{*}\bigr] \\ &\quad {} + \frac{1}{2}\bigl(\hat{\boldsymbol{\eta}}_{m}^{*} - \mathbf{A}\boldsymbol{\mu}_{m}\bigr)^{\operatorname{T}} \bigl( \mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}} \bigr)^{ - 1}\bigl(\hat{\boldsymbol{\eta}}_{m}^{*} - \mathbf{A}\boldsymbol{\mu}_{m}\bigr) \\ &\quad {}+ \frac{1}{2}Q\log2\pi- \frac{1}{2}\log \bigl|\bigl( \mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}} \bigr)^{ - 1}\bigr| - \frac{1}{2}\log \bigl|\hat{\mathbf{R}}_{m}^{*}\bigr| \\ &\quad {}+ \frac{1}{2}\log \bigl|\hat{\mathbf{R}}_{m}^{*}\bigr| - \frac{1}{2}Q + \frac{1}{2}Q - \log\omega_{m} \end{aligned}$$

(38)

Express the KL divergence of a zero-mean Q-variate normal density with covariance matrix Σ ₂ from a zero-mean Q-variate normal density with covariance matrix Σ ₁ as

$$ \mathrm{KL}_{\mathrm{norm}}[\varSigma_{1}|\varSigma_{2}] = \frac{1}{2}\operatorname{tr} \bigl[\varSigma_{2}^{ - 1} \varSigma_{1}\bigr] - \frac{1}{2}\log \bigl|\varSigma_{2}^{ - 1} \varSigma_{1}\bigr| - \frac{1}{2}Q $$

(39)

Then (38) can be formulated in the following form:

$$\begin{aligned} \mathbf{H}_{m} & = \underbrace{\frac{1}{2}\operatorname{tr} \bigl[\bigl(\mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}\bigr)^{ - 1}\hat{\mathbf{R}}_{m}^{*} \bigr] - \frac{1}{2}\log \bigl|\bigl(\mathbf{AC}_{m} \mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}\bigr)^{ - 1}\hat{ \mathbf{R}}_{m}^{*}\bigr| - \frac{1}{2}Q}_{\operatorname{KL}_{\mathrm{norm}}[\hat{\mathbf{R}}_{m}^{*}|\mathbf {AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}]} \\ &\quad {}+ \frac{1}{2}\bigl(\hat{\boldsymbol{\eta}}_{m}^{*} - \mathbf{A}\boldsymbol{\mu}_{m}\bigr)^{\operatorname{T}} \bigl( \mathbf{AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}} \bigr)^{ - 1}\bigl(\hat{\boldsymbol{\eta}}_{m}^{*} - \mathbf{A}\boldsymbol{\mu}_{m}\bigr) \\ &\quad {} + \underbrace{\frac{1}{2}Q \log2\pi e + \frac{1}{2}\log \bigl|\hat{\mathbf{R}}_{m}^{*}\bigr| - \log\omega_{m}}_{\mathrm{const}} \end{aligned}$$

(40)

where $\mathrm{KL}_{\mathrm{norm}}[\hat{\mathbf{R}}_{m}^{*}|\mathbf {AC}_{m}\mathbf{A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}]$ is the KL divergence between two zero-mean Q-variate normal densities with a covariance matrix $\hat{\mathbf{R}}_{m}^{*}$ and $\mathbf{AC}_{m}\mathbf {A}^{\operatorname{T}} + \mathbf{R}_{\mathbf{w}}$, respectively. Therefore, (20) can be derived by inserting (40) into (37).