Letter to the Editor: On the Numerical Evaluation of Bandpass Prolates

Abstract

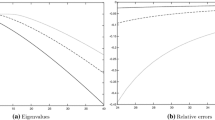
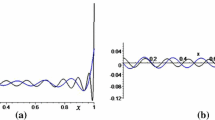
This letter provides a technique for numerical evaluation of certain eigenfunctions of the integral kernel operator corresponding to time truncation of a square-integrable function to a finite interval, followed by frequency limiting to frequencies in an annular band.

Appendices

Appendix A: Proof of Proposition 2

One has

Interchanging the roles of n and m one has

Subtracting the two results in the identity

$$(\chi_n-\chi_m ) \int_x^1 \varphi_n(t) \varphi_m(t) \,\mathrm {d}t = \bigl(t^2-1 \bigr) \biggl({\mathrm {d}\varphi_n\over \mathrm {d}t} \varphi_m (t) -{\mathrm {d}\varphi_m\over \mathrm {d}t} \varphi_n (t) \biggr) \biggm{|}_x^1 . $$

Appendix B: Proof of Proposition 1

Suppose that $\psi=\sum \alpha_{n} \varphi_{n}^{c}$ with $\varphi_{n}^{c}$ L ²(ℝ)-normalized. Then

where in the last line we use the fact that $\{\varphi_{j}^{c}\}$ is complete in PW _c and PW _c′⊂PW _c . Use of the Plancherel identity, Eq. (3), the eigenfunction property of the prolates and the property P _c P _c′=P _c′ P _c =P _c′, shows that the quantity $\langle P_{c'}Q\varphi_{k}^{c},\varphi_{j}^{c}\rangle$ in the last line of the formula above may be written as

That is, for $\psi=\sum_{k} \alpha_{k} \varphi_{k}^{c}$ one has

$$P_{c'c} Q\psi =\sum_k \alpha_k\lambda_k \biggl(\varphi_k^c- \sum_j R_{jk} \varphi_j^c \biggr) . $$

Thus if P _c′c Qψ=λψ then

$$\lambda \alpha_j =\lambda_j \alpha_j -\sum _k \lambda_k \alpha_k R_{jk} $$

or, equivalently, λ α=(I−R)Λ α with α={α _k }.

Notice that if α∈ℓ ²(ℤ₊) and f _α ∈L ²[−1,1] is defined by $f_{\alpha}(t)=\sum_{k}{\mathrm {i}^{k}\over\sqrt{\lambda_{k}} }\overline{\alpha_{k}} \varphi_{k}^{c}$ then

$$\langle R\alpha, \alpha\rangle =\int_{-c'/c}^{c'/c} \big|f_\alpha(t)\big|^2 \,\mathrm {d}t $$

and, since R is self adjoint,

$$\|I-R\|=\sup_{\boldsymbol{\alpha}:\|\boldsymbol{\alpha}\|=1} \bigl\langle (I-R)\boldsymbol{\alpha}, \boldsymbol{\alpha}\bigr\rangle = \sup_{\boldsymbol{\alpha}} \int_{c'/c\leq |t|\leq 1}\big|f_\alpha(t)\big|^2 \,\mathrm {d}t . $$