Skip to main content
SpringerLink
Log in

A short numerical study on the optimization methods influence on topology optimization

  • DISCUSSION
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

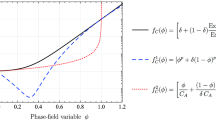
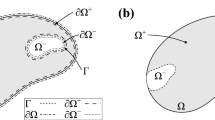
Abstract

Structural topology optimization problems are commonly defined using continuous design variables combined with material interpolation schemes. One of the challenges for density based topology optimization observed in the review article (Sigmund and Maute Struct Multidiscip Optim 48(6):1031–1055 2013) is the slow convergence that is often encountered in practice, when an almost solid-and-void design is found. The purpose of this forum article is to present some preliminary observations on how designs evolves during the optimization process for different choices of optimization methods. Additionally, the authors want to open a discussion on how to properly define and identify the boundary translation that is often observed in practice. The authors hope that these preliminary observations can open for fruitful discussions and stimulate further investigations concerning slowly moving boundaries. Although the discussion is centered on density based methods it may be equally relevant to level-set and phase-field approaches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. In this manuscript the word solve (in the context of optimization problems) should be understood as finding a point numerically satisfying the KKT conditions within some prescribed tolerances.

  2. Number of optimization sub-problems solved.

  3. The KKT condition of IPOPT cannot be obtained with the interface used in these numerical examples, and thus cannot be presented in Fig. 9.

References

  • Amestoy PR, Duff IS, L’Excellent JY (2000) Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput Methods Appl Mech Eng 184(2–4):501–520

    Article  MATH  Google Scholar 

  • Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O (2011) Efficient topology optimization in MATLAB using 88 lines of code. Struct Multidiscip Optim 43(1):1–16

    Article  MATH  Google Scholar 

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):192–202

    Article  Google Scholar 

  • Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69(9–10):635–654

    MATH  Google Scholar 

  • Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications. Springer-Verlag, Berlin Heidelberg

    MATH  Google Scholar 

  • Boggs PT, Tolle JW (1995) Sequential quadratic programming. Acta Numerica 4:1–51

    Article  MATH  MathSciNet  Google Scholar 

  • Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(9):2143–2158

    Article  MATH  MathSciNet  Google Scholar 

  • Byrd RH, Hribar ME, Nocedal J (1999) An interior point algorithm for large-scale nonlinear programming. SIAM J Optim 9(4):877–900

    Article  MATH  MathSciNet  Google Scholar 

  • Dennis JE, Moré JJ (1977) Quasi-Newton methods, motivation and theory. SIAM Rev 19(1):46–89

    Article  MATH  MathSciNet  Google Scholar 

  • Forsgren A, Gill PE (1998) Primal-dual interior methods for nonconvex nonlinear programming. SIAM J Optim 8(4):1132–1152

    Article  MATH  MathSciNet  Google Scholar 

  • Morales JL, Nocedal J, Wu Y (2010) A sequential quadratic programming algorithm with an additional equality constrained phase. J Numer Anal 32(2):553–579

    Article  MATH  MathSciNet  Google Scholar 

  • Nocedal J (1980) Updating Quasi-Newton matrices with limited storage. Math Comput 35(151):773–782

    Article  MATH  MathSciNet  Google Scholar 

  • Nocedal J, Wright SJ (1999) Numerical optimization. Springer-Verlag, Berlin Heidelberg

    Book  MATH  Google Scholar 

  • Nocedal J, Wächter R, Waltz RA (2009) Adaptive barrier update strategies for nonlinear interior methods. SIAM J Optim 19(4):1674–1693

    Article  MATH  MathSciNet  Google Scholar 

  • Rojas-Labanda S, Stolpe M (2015) Benchmarking optimization solvers for structural topology optimization. Struct Multidiscip Optim 52(3):527–547

    Article  MathSciNet  Google Scholar 

  • Rojas-Labanda S, Stolpe M (2016) An efficient second-order SQP method for structural topology optimization. Struct Multidiscip Optim 53(6):1315–1333

    Article  MathSciNet  Google Scholar 

  • Rozvany GIN, Zhou M (1991) The COC algorithm, part I: cross-section optimization or sizing. Comput Methods Appl Mech Eng 89(1–3):281–308

    Article  Google Scholar 

  • Sigmund O (1997) On the design of compliant mechanisms using topology optimization. J Struct Mech 25(4):492–526

    Google Scholar 

  • Sigmund O (2009) Manufacturing tolerant topology optimization. Acta Mech Sinica 25(2):227–239

    Article  MATH  Google Scholar 

  • Sigmund O, Maute K (2013) Topology optimization approaches. Struct Multidiscip Optim 48(6):1031–1055

    Article  MathSciNet  Google Scholar 

  • Svanberg K (1987) The method of moving asymptotes - a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    Article  MATH  MathSciNet  Google Scholar 

  • Wächter A, Biegler LT (2006) On the implementation of an interior point filter line-search algorithm for large-scale nonlinear programming. Math Program 106(1):25–57

    Article  MATH  MathSciNet  Google Scholar 

  • Yamashita H (1998) A globally convergent primal-dual interior point method for constrained optimization. Optim Methods Softw 10(2):2–4

    Article  MATH  MathSciNet  Google Scholar 

  • Zhou M, Rozvany GIN (1991) The COC algorithm, Part II: topological, geometrical and generalized shape optimization. Comput Methods Appl Mech Eng 89(1–3):309–336

    Article  Google Scholar 

Download references

Acknowledgements

We would like to thank Professor Krister Svanberg at KTH in Stockholm for providing the implementation of MMA. We also express our sincere thanks to the two reviewers and the editor for their honest comments and suggestions which lead to improvements of the article.

Author information

Authors and Affiliations

  1. Department of Wind Energy, Technical University of Denmark, Frederiksborgvej 399, 4000, Roskilde, Denmark

    Susana Rojas-Labanda & Mathias Stolpe

  2. Department of Mechanical Engineering, Technical University of Denmark, Nils Koppels Allé, Building 404, 2800, Kgs. Lyngby, Denmark

    Ole Sigmund

Authors
  1. Susana Rojas-Labanda
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ole Sigmund
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mathias Stolpe
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Susana Rojas-Labanda.

Additional information

This research is funded by the Villum Foundation through the research project Topology Optimization – the Next Generation (NextTop).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rojas-Labanda, S., Sigmund, O. & Stolpe, M. A short numerical study on the optimization methods influence on topology optimization. Struct Multidisc Optim 56, 1603–1612 (2017). https://doi.org/10.1007/s00158-017-1813-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1813-2

Keywords

Search

Navigation