Abstract
The adverse effects of multicollinearity and unusual observations are seen in logistic regression and attention had been given in the literature to each of these problems separately. However, multicollinearity and unusual observations can arise simultaneously in logistic regression. The objective of this paper is to propose the statistics for detecting the unusual observations in an ill-conditioned data set under the ridge logistic estimator. A numerical example and two Monte Carlo simulation studies are used to illustrate the methodology. The present investigation shows that ridge logistic estimation copes with unusual observations by downweighting their influence.



Similar content being viewed by others
Notes
For the iterative scheme given by Eq. (2), \(\varvec{\hat{\beta }}^{(0)}\) is used as an initial value; however, to start the iteration \(\varvec{ \hat{\beta }}^{(0)}\) should be known. Therefore, a real parameter value, say \( \varvec{\beta }_{0}\), is usually used. Hence, \(\varvec{\hat{\beta }} ^{(0)}\) and \(\varvec{\beta }_{0}\) can be used interchangeably.
The main difference between the ridge estimators of Schaefer et al. (1984) and LeCessie and VanHouwelingen (1992) is that the ML estimator at convergence is used in computing matrix V of the estimator of Schaefer et al. (1984) whereas real parameter value \(\varvec{\beta }_{0}\) is used in computing matrix V of the estimator of LeCessie and VanHouwelingen (1992).
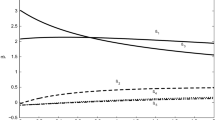
The ridge logistic estimates in Fig. 3 correspond to first-order estimates. The first-order ML estimate of \(\varvec{\beta }\) is computed as \( [-2.2852,0.0165,0.7830,-0.0063,0.9336,2.7695]\) which is seen from Fig. 3 for \(k=0\). Therefore, the estimated values on Fig. 3 for \(k=0\) are different from the fully iterated ML estimates in Table 13.
References
Atkinson AC (1985) Plots, transformations and regression. Clarendon Press, Oxford
Cook RD (1977) Detection of influential observation in linear regression. Technometrics 19(1):15–18
Cook D, Weisberg S (1982) Residuals and influence in regression. Chapman and Hall, New York
Duffy DE, Santner TJ (1989) On the small sample properties of norm restricted maximum likelihood estimators for logistic regression models. Commun Stat Theory Methods 18(3):959–980
Hoerl AE, Kennard RW, Baldwin KF (1975) Ridge regression: some simulations. Commun Stat Theory Methods 4(2):105–123
Hosmer DW, Lemeshow S, Sturdivant RX (2013) Applied logistic regression, 3rd edn. Wiley, Hoboken
Jahufer A, Jianbao C (2009) Assessing global influential observations in modified ridge regression. Stat Probab Lett 79(4):513–518
Jennings DE (1986) Outliers and residual distributions in logistic regression. J Am Stat Assoc 81(396):987–990
Lee AH, Silvapulle MJ (1988) Ridge estimation in logistic regression. Commun Stat Simul 17(4):1231–1257
LeCessie S, VanHouwelingen JC (1992) Ridge estimators in logistic regression. Appl Stat 41(1):191–201
Lesaffre E, Albert A (1989) Multiple group logistic regression diagnostics. J R Stat Soc Ser C Appl Stat 38:425–440
Lesaffre E, Marx BD (1993) Collinearity in generalized linear regression. Commun Stat Theory Methods 22(7):1933–1952
McDonald GC, Galarneau DI (1975) A Monte Carlo evaluation of some ridge-type estimators. J Am Stat Assoc 70(350):407–416
McCullagh P, Nelder JA (1989) Generalized linear models, 2nd edn. Chapman & Hall, Boca Raton
Özkale MR (2013) Influence measures in affine combination type regression. J Appl Stat 40(10):2219–2243
Pregibon D (1981) Logistic regression diagnostics. Ann Stat 9(4):705–724
Preisser JS, Garcia DI (2005) Alternative computational formulae for generalized linear model diagnostics: identifing influential observations with SAS software. Comput Stat Data Anal 48:755–764
Schaefer RL, Roi LD, Wolfe RA (1984) A ridge logistic estimator. Commun Stat Theory Methods 13(1):99–113
Schott JR (2005) Matrix analysis for statistics. Wiley, Hoboken
Smith EP, Marx BD (1990) Ill-conditioned information matrices, generalized linear models and estimation of the effects of acid rain. Environmetrics 1(1):57–71
Wahba G, Golub GH, Heath M (1979) Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21(2):215–223
Walker E, Birch JB (1988) Influence measures in ridge regression. Technometrics 30(2):221–227
Weissfeld LA, Sereika SM (1991) A multicollinearity diagnostics for generalized linear models. Commun Stat Theory Methods 20(4):1183–1198
Williams DA (1987) Generalized linear model diagnostics using the deviance and single case deletions. J R Stat Soc Ser C Appl Stat 36(2):181–191
Acknowledgements
This research was supported by The Scientific and Technological Research Council of Turkey (TÜBİTAK) to M. Revan Özkale, a visiting scholar for 5 months by TÜBİTAK to The Ohio State University, College of Public Health, Division of Biostatistics.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
Theorem 1
The \(\varvec{\hat{\beta }}^{(1)}(k)\) when the \(i\hbox {th}\) observation is deleted is \(\varvec{\hat{\beta }}_{(i)}^{(1)}(k)= \varvec{\hat{\beta }}^{(1)}(k)-\frac{(X^{\prime }V^{(0)}X+kI)^{-1}x_{i}}{ 1-h_{ii}(k)}v_{ii}^{(0)}[z_{i}^{(0)}-x_{i}^{\prime }\varvec{\hat{\beta }} ^{(1)}(k)]\) where \(\sqrt{v_{ii}^{(0)}}[z_{i}^{(0)}-x_{i}^{\prime } \varvec{\hat{\beta }}^{(1)}(k)]\) is the \(i\hbox {th}\) ridge logistic regression residual and \(h_{ii}(k)\) is the \(i\hbox {th}\) ridge logistic regression leverage value.
Proof
Let \(Q=(V^{(0)})^{1/2}X\), \(\mathbf {w}=(V^{(0)})^{1/2}\mathbf {z}^{(0)}\) and \(\mathbf {s}=\mathbf {y}-\hat{\mathbf {\pi }}^{(0)}\). Then \(\varvec{\hat{ \beta }}^{(1)}(k)\) and \(\varvec{\hat{\beta }}^{(1)}\) given by (4) and (5) can be reexpressed as
and
Let \(\varvec{\hat{\beta }}_{(i)}^{(1)}(k)\) and \(\varvec{\hat{\beta }} _{(i)}^{(1)}\) denote the ML and ridge logistic estimators of \(\varvec{ \beta }\) based on the observations without the \(i\hbox {th}\) observation, respectively. Then, we have
and
By applying the Sherman–Morrison–Woodbury theorem (see Schott 2005) to \( (Q_{(i)}^{\prime }Q_{(i)})^{-1}\) and after algebraic simplifications, \( \varvec{\hat{\beta }}_{(i)}^{(1)}\) can be written as
where \(q_{i}^{\prime }=\sqrt{v_{ii}^{(0)}}x_{i}^{\prime }\) is the ith row vector of the Q matrix and \(h_{ii}=q_{i}^{\prime }(Q^{\prime }Q)^{-1}q_{i}=v_{ii}^{(0)}x_{i}^{\prime }(X^{\prime }V^{(0)}X)^{-1}x_{i}\) is the \(i\hbox {th}\) diagonal element of
Noting that \((Q^{\prime }Q)^{-1}X^{\prime }\mathbf {s}=\varvec{\hat{\beta } }^{(1)}-\varvec{\hat{\beta }}^{(0)}\), \(\varvec{\hat{\beta }} _{(i)}^{(1)}\) can be written as
where \(\frac{s_{i}}{v_{ii}^{(0)}}+x_{i}^{\prime }\varvec{\hat{\beta }} ^{(0)}\) is the \(i\hbox {th}\) element of working response \(\mathbf {z}^{(0)}\). Then \( \sqrt{v_{ii}^{(0)}}(\frac{s_{i}}{v_{ii}^{(0)}}+x_{i}^{\prime }\varvec{ \hat{\beta }}^{(0)}\mathbf {-}x_{i}^{\prime }\varvec{\hat{\beta }}^{(1)})\) presents the \(i\hbox {th}\) standardized residual (Pearson residual) after one step iteration. \(\square \)
Using the expression
where \(h_{ii}(k)=q_{i}^{\prime }(Q^{\prime }Q+kI)^{-1}q_{i}=v_{ii}^{(0)}x_{i}^{\prime }(X^{\prime }V^{(0)}X+kI)^{-1}x_{i}\) is the \(i\hbox {th}\) diagonal element of the matrix \( H(k)=(V^{(0)})^{1/2}X(X^{\prime }V^{(0)}X+kI)^{-1}X^{\prime }(V^{(0)})^{1/2}\), we obtain
Substituting results (11) and (12) into (10) and after algebraic simplifications, we obtain
Since \(\frac{s_{i}}{v_{ii}^{(0)}}+x_{i}^{\prime }\varvec{\hat{\beta }} ^{(0)}\) is the \(i\hbox {th}\) element of working response \(\mathbf {z}^{(0)}\), the proof is completed when Q and \(q_{i}\) are written as defined earlier.
Appendix B
Theorem 2
The change in Pearson chi-square statistic for the ridge logistic estimator is
Proof
Let \(\chi ^{2}(k)\) and \(\chi _{(i)}^{2}(k)\) denote the Pearson chi-square statistic based on the full data set and the Pearson chi-square statistic when observation i is deleted for the ridge logistic estimator. Then, by using the linear regression-like approximation of Pregibon (1981), we get the following expressions which are similar to residual sum of squares in linear regression:
and
The expression \(\varvec{\hat{\beta }}_{(i)}^{(1)}(k)\) given by Theorem 1 can also be written as
By using this expression, we get
and
Hence, we obtain \(\chi _{(i)}^{2}(k)\) from Eqs. (13) and (14) as \(\square \)
\(\chi _{(i)}^{2}(k)\) reduces to
The difference \(\Delta \chi _{i}^{2}(k)=\chi ^{2}(k)-\chi _{(i)}^{2}(k)\), after algebraic simplifications, equals
Using the definition of \(w_{i}\), \(q_{i}\) and Q, the proof is completed.
Rights and permissions
About this article
Cite this article
Özkale, M.R., Lemeshow, S. & Sturdivant, R. Logistic regression diagnostics in ridge regression. Comput Stat 33, 563–593 (2018). https://doi.org/10.1007/s00180-017-0755-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-017-0755-x