Skip to main content
SpringerLink
Log in

Effective Behavior of Nematic Elastomer Membranes

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

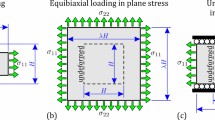
We derive the effective energy density of thin membranes of liquid crystal elastomers as the \({\Gamma}\) -limit of a widely used bulk model. These membranes can display fine-scale features both due to wrinkling that one expects in thin elastic membranes and due to oscillations in the nematic director that one expects in liquid crystal elastomers. We provide an explicit characterization of the effective energy density of membranes and the effective state of stress as a function of the planar deformation gradient. We also provide a characterization of the fine-scale features. We show the existence of four regimes: one where wrinkling and microstructure reduces the effective membrane energy and stress to zero, a second where wrinkling leads to uniaxial tension, a third where nematic oscillations lead to equi-biaxial tension and a fourth with no fine scale features and biaxial tension. Importantly, we find a region where one has shear strain but no shear stress and all the fine-scale features are in-plane with no wrinkling.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ball, J.M., James, R.D.: Incompatible sets of gradients and metastability. Arch. Rational Mech. Anal. (2015). doi:10.1007/s00205-015-0883-9

  2. Ball J., Kirchheim B., Kristensen J.: Regularity of quasiconvex envelopes. Calc. Var. 11, 333–359 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ball, J., Murat, F.: W 1,p-Quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58, 225–253 (1984)

  4. Barchiesi, M. and DeSimone, A.: Frank energy for nematic elastomers: a nonlinear model, ESAIM: COCV 21(2), 372–377 (2015)

  5. Bhattacharya K., James R.D.: A theory of thin films of martensitic materials with applications to microactuators. J. Mech. Phys. Solids 47, 531–576 (1999)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  6. Bladon, P., Terentjev, E.M., Warner, M.: Transitions and instabilities in liquid-crystal elastomers. Phys. Rev. E 47, R3838–R3840 (1993)

  7. Braides, A.: \({\Gamma}\) -Convergence for Beginners. Oxford University Press, Oxford, 2002

  8. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge, 2004

  9. Conti, S., DeSimone, A., Dolzmann, G.: Soft elastic response of stretched sheets of nematic elastomers: a numerical study. J. Mech. Phys. Solids 50, 1431–1451 (2002)

  10. Conti, S., Dolzmann, G.: Derivation of elastic theories for thin sheets and the constraint of incompressibility. In: Analysis, Modeling and Simulation of Multiscale Problems, pp. 225–246. Springer, 2006

  11. Dacorogna, B.: Direct Methods in the Calculus of Variations, 2nd edn. Springer, New York, 2008

  12. Del Maso, G.: An Introduction to \({\Gamma}\) -Convergence. Birkhäuser, Boston, 1993

  13. DeSimone A.: Energy minimizer for large ferromagnetic bodies. Arch. Rat. Mech. Anal. 125, 99–143 (1993)

    Article  MathSciNet  Google Scholar 

  14. DeSimone, A., Dolzmann, G.: Macroscopic response of nematic elastomers via relaxation of a class of O(3)-invariant energies.Arch. Rat. Mech. Anal. 161 181–204 (2002)

  15. de Gennes, P.G. and Prost, J.: The Physics of Liquid Crystals. Oxford University Press, Oxford, 1993

  16. Frank, F.C., Liquid crystals, I.: On the theory of liquid crystals. Faraday Soc. 25, 19–28 (1958)

  17. Fonseca, I., Gangbo, W.: Local invertibility of sobolev functions. SIAM J. Math. Anal. 26(2), 280–304 (1995)

  18. Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: L P Spaces, Springer Monographs in Mathematics (2007)

  19. Kinderlehrer, D., Pedregal, P.: Characterizations of Young measures generated by gradients. Arch. Rat. Mech. Anal. 115, 329–365 (1991)

  20. Kinderlehrer, D., Pedregal, P.: Weak convergence of integrands and the Young measure representation. SIAM J. Math. Anal. 23(1), 1–19 (1992)

  21. Kundler, I., Finkelmann, H.: Strain-induced director reorientation in nematic liquid single crystal elatomers. Macromol. Chem. Rap. Commun. 16, 679–686 (1995)

  22. Olmsted, P.D.: Rotational invariance and Goldstone modes in nematic elastomers and gels. J. de Phy. II. 4, 2215–2230 (1994)

  23. Le Dret, H., Raoult, A.: The nonlinear membrane model as variational limit of nonlinear three-dimensional elasticity. J. Math Pures Appl. 74, 549–578 (1995)

  24. Müller, S.: Variational methods for microstructure and phase transitions. In: Bethuel, F., Huisken, G., Müller, S., Steffen, K., Hildebrandt, S., Strüwe, M. (eds.) Proceedings of the C.I.M.E. summer school “Calculus of variation and geometric evolution problems”, Cetraro 1996, Springer LNM, vol. 1713, 1999

  25. Mansfield E.H.: Load transfer via a wrinkled membrane. Proc. R. Soc. Lond A 316, 269–289 (1970)

    Article  ADS  Google Scholar 

  26. Pipkin, A.C.: The relaxed energy density for isotropic elastic membranes. IMA J. Appl. Math. 36, 85–99 (1986)

  27. Qi, L., Wormersley, R.S.: On extreme singular values of matrix valued functions. J. Convex Anal. 3, 153–166 (1996)

  28. Steigmann, D.J., Pipkin, A.C.: Finite deformations of wrinkled membranes. Q.J. Mech. Appl. Math. 42, 427–440 (1989)

  29. Shu, Y.C.: Heterogeneous thin films of martensitic materials. Arch. Rational Mech. Anal. 153, 39–90 (2000)

  30. Trabelsi, K.: Incompressible nonlinearly elastic thin membranes. C. R. Acad. Sci. Paris, Ser. I 340, 75–80 (2005)

  31. Trabelsi, K.: Modeling of a membrane for nonlinearly elastic incompressible via Gamma-convergence. Anal. Appl. 4(1), 31–60 (2006)

  32. Warner, M., Bladon, P., and Terentjev, E.M.: Soft elasticity—deformation without resistance in liquid crystal elastomers. J. de Phys. II 4, 93–102 (1994)

  33. Warner, M., Terentjev, E.M.: Liquid Crystal Elastomers. Oxford Science Publ., Oxford, 2003

  34. Yan B.: An explicit formula of reduced membrane energy for incompressible p-Dirichlet energy. Appl. Anal. 88(9), 1321–1327 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematical Institute, Woodstock Road, Oxford, OX26GG, England

    Pierluigi Cesana

  2. California Institute of Technology, Pasadena, CA, 91125, USA

    Paul Plucinsky & Kaushik Bhattacharya

Authors
  1. Pierluigi Cesana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paul Plucinsky
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kaushik Bhattacharya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kaushik Bhattacharya.

Additional information

Communicated by The Editors

Dedicated to Jerald L. Ericksen on the occasion of his 90th birthday

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cesana, P., Plucinsky, P. & Bhattacharya, K. Effective Behavior of Nematic Elastomer Membranes. Arch Rational Mech Anal 218, 863–905 (2015). https://doi.org/10.1007/s00205-015-0871-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-015-0871-0

Keywords

Search

Navigation