Abstract
Given a vector field \(\rho (1,\mathbf {b}) \in L^1_\mathrm{loc}(\mathbb {R}^+\times \mathbb {R}^{d},\mathbb {R}^{d+1})\) such that \({{\,\mathrm{div}\,}}_{t,x} (\rho (1,\mathbf {b}))\) is a measure, we consider the problem of uniqueness of the representation \(\eta \) of \(\rho (1,\mathbf {b}) {\mathcal {L}}^{d+1}\) as a superposition of characteristics \(\gamma : (t^-_\gamma ,t^+_\gamma ) \rightarrow \mathbb {R}^d\), \(\dot{\gamma } (t)= \mathbf {b}(t,\gamma (t))\). We give conditions in terms of a local structure of the representation \(\eta \) on suitable sets in order to prove that there is a partition of \(\mathbb {R}^{d+1}\) into disjoint trajectories \(\wp _\mathfrak {a}\), \(\mathfrak {a}\in \mathfrak {A}\), such that the PDE
can be disintegrated into a family of ODEs along \(\wp _\mathfrak {a}\) with measure r.h.s. The decomposition \(\wp _\mathfrak {a}\) is essentially unique. We finally show that \(\mathbf {b}\in L^1_t({{\,\mathrm{BV}\,}}_x)_\mathrm{loc}\) satisfies this local structural assumption and this yields, in particular, the renormalization property for nearly incompressible \({{\,\mathrm{BV}\,}}\) vector fields.












Similar content being viewed by others
References
Alberti, G., Bianchini, S., Crippa, G.: Structure of level sets and Sard-type properties of Lipschitz maps. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 12(4), 863–902 (2013)
Alberti, G., Bianchini, S., Crippa, G.: A uniqueness result for the continuity equation in two dimensions. JEMS 16(2), 201–234 (2014)
Ambrosio, L., Bouchut, F., De Lellis, C.: Well-posedness for a class of hyperbolic systems of conservation laws in several space dimensions. Commun. Partial Differ. Equ. 29(9–10), 1635–1651 (2004)
Ambrosio, L., Crippa, G.: Existence, uniqueness, stability and differentiability properties of the flow associated to weakly differentiable vector fields. In: Transport Equations and Multi-D Hyperbolic Conservation Laws, volume 5 of Lecture Notes of the Unione Matematica Italiana. Springer, Berlin, pp. 3–57 (2008)
Ambrosio, L., Crippa, G., Maniglia, S.: Traces and fine properties of a \(\text{ BD }\) class of vector fields and applications. Ann. Fac. Sci. Toulouse Math. (6) 14(4), 527–561 (2005)
Ambrosio, L., De Lellis, C.: Existence of solutions for a class of hyperbolic systems of conservation laws in several space dimensions. Int. Math. Res. Not. 41, 2205–2220 (2003)
Ambrosio, L., De Lellis, C., Malý, J.: On the chain rule for the divergence of BV-like vector fields: applications, partial results, open problems. In: Perspectives in Nonlinear Partial Differential Equations, volume 446 of Contemporary Mathematics. American Mathematical Society, Providence, RI, pp. 31–67 (2007)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Science Publications, Oxford (2000)
Alberti, G.: Rank one property for derivatives of functions with bounded variation. Proc. R. Soc. Edinb. Sect. A 123(2), 239–274 (1993)
Ambrosio, L.: Transport equation and Cauchy problem for BV vector fields. Invent. math. 158(2), 227–260 (2004)
Anzellotti, G.: Traces of bounded vectorfields and the divergence theorem (1983)
Babadjian, J.-F.: Traces of functions of bounded deformation. Indiana Univ. Math. J. 64, 1271–1290 (2015)
Bianchini, S., Bonicatto, P., Gusev, N.A.: Renormalization for autonomous nearly incompressible BV vector fields in two dimensions. SIAM J. Math. Anal. 48(1), 1–33 (2016)
Bianchini, S., Gloyer, M.: An estimate on the flow generated by monotone operators. Commun. Partial Differ. Equ. 36(5), 777–796 (2011)
Bianchini, S., Gusev, N.A.: Steady nearly incompressible vector fields in two-dimension: chain rule and renormalization. Arch. Ration. Mech. Anal. 222(2), 451–505 (2016)
Bonicatto, P.: Untangling of trajectories for non-smooth vector fields and Bressans Compactness Conjecture. PhD thesis, SISSA (2017)
Bressan, A.: An ill posed Cauchy problem for a hyperbolic system in two space dimensions. Rend. Sem. Mat. Univ. Padova 110, 103–117 (2003)
Bressan, A.: A lemma and a conjecture on the cost of rearrangements. Rend. Sem. Mat. Univ. Padova 110, 97–102 (2003)
De Lellis, C.: Notes on hyperbolic systems of conservation laws and transport equations. In: Handbook of Differential Equations: Evolutionary Equations. Vol. III, Handbook of Differential Equations. Elsevier, Amsterdam, pp. 277–382 (2007)
De Lellis, C.: A note on Alberti’s rank-one theorem. In: Transport Equations and Multi-D Hyperbolic Conservation Laws, volume 5 of Lecture Notes of the Unione Matematica Italiana. Springer, Berlin, pp. 61–74 (2008)
Depauw, N.: Non-unicité du transport par un champ de vecteurs presque BV. In: Seminaire: Équations aux Dérivées Partielles, 2002–2003, Sémin. Équ. Dériv. Partielles, pages Exp. No. XIX, 9. École Polytech., Palaiseau (2003)
DiPerna, R.J., Lions, P.-L.: Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98(3), 511–547 (1989)
Fremlin, D.H.: Measure Theory. Vol. 4. Torres Fremlin, Colchester, 2006. Topological Measure Spaces. Part I, II, Corrected second printing of the 2003 original
Gagliardo, E.: Caratterizzazioni delle tracce sulla frontiera relative ad alcune classi di funzioni in \(n\) variabili. Rend. Sem. Mat. Univ. Padova 27, 284–305 (1957)
Kellerer, H.G.: Duality theorems for marginal problems. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 67(4), 399–432 (1984)
Keyfitz, B.L., Kranzer, H.C.: A system of nonstrictly hyperbolic conservation laws arising in elasticity theory. Arch. Ration. Mech. Anal. 72(3), 219–241 (1979/80)
Morse, A.P.: Perfect blankets. Trans. Am. Math. Soc. 61(3), 418–442 (1947)
Paolini, E., Stepanov, E.: Decomposition of acyclic normal currents in a metric space. J. Funct. Anal. 263(11), 3358–3390 (2012)
Paolini, E., Stepanov, E.: Structure of metric cycles and normal one-dimensionalcurrents. J. Funct. Anal. 264(6), 1269–1295 (2013)
Smirnov, S.K.: Decomposition of solenoidal vector charges into elementary solenoids and the structure of normal one-dimensional currents. St. Petersb. Math. J. 5(4), 841–867 (1994)
Ziemer, W.P.: Weakly Differentiable Functions: Sobolev Spaces and Functions of Bounded Variation, Graduate Texts in Mathematics. Springer, New York (1989)
Acknowledgements
The authors would like to thank the Center of Mathematical Sciences and Applications (CMSA) of Harvard University and the Institut des Hautes Études Scientifiques (IHES) where part of this work has been done. They are also grateful to Guido de Philippis for useful discussions. During the revision of the paper, the second author was supported by ERC Starting Grant 676675 FLIRT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Alberto Bressan on the occasion of his 60th birthday
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Glossary
Glossary
- \({\mathrm {Cyl}}_{t,x}^{r,L}\) :
-
\(\rho (1,\mathbf {b})\)-proper cylinder
- \(\nu \ll \mu \) :
-
\(\nu \) is absolute continuous w.r.t. \(\mu \)
- \(\fint _A f \, \mu \) :
-
Average integral on the sets A
- \(D^\mathrm {a.c.}\mathbf {b}\) :
-
Absolutely continuous part of Df
- \(\phi ^\ell _\gamma \) :
-
Approximate cylinder of flow
- \(J_{\mathbf {b}}\) :
-
Approximate jump set of \(\mathbf {b}\)
- \(\nu ^\mathrm {a.c.}\) :
-
Absolutely continuous part of \(\nu \)
- \(Q_{\ell ^-_{1,\gamma },\ell _{1,\gamma }^+,\ell }\) :
-
Approximate cylinder with shape determined by \(\ell ^\pm _{1,\gamma },\ell \)
- \(B^d_r(x)\) :
-
Balls of radius r centered at \(x \in \mathbb {R}^d\)
- \({{\,\mathrm{Fr}\,}}A\) :
-
Boundary of a set A
- \(\partial \Omega \) :
-
Boundary of a set in \(\mathbb {R}^d\)
- \({\bar{Q}}\) :
-
Base of the cylinder \(Q_{\ell ^\pm _{1,\gamma },\ell }\)
- \(A^c\) :
-
Complementary set of A
- \(C({\mathbf {e}}, a)\) :
-
Closed convex cone about \(\varepsilon \) of vertex 0 ant openint a
- \(C({\mathbf {e}}, a; x)\) :
-
Closed convex cone about \(\varepsilon \) of vertex x ant openint a
- \({\mathbb {1}}_A\) :
-
Characteristic function of the set A
- \({{\,\mathrm{clos}\,}}A\) :
-
Closure of the set A
- \(C_c^\infty (\Omega )\) :
-
Compactly supported smooth functions defined in the open set \(\Omega \subset \mathbb {R}^d\)
- \(*\) :
-
Convolution in \(\mathbb {R}^d\)
- \(D^{\mathrm {cantor}}\mathbf {b}\) :
-
Cantor part of \(D^{\mathrm {sing}}f\)
- \(\gamma \) :
-
Curve defined in an interval of time
- \(g \circ f\) :
-
Composition of two functions
- \(K_{{\bar{r}}}^{\varepsilon ,\varepsilon '} \subset K^{\varepsilon }\) :
-
Compact subset of \(\partial \Omega \) defined in Lemma 4.16
- \(K^\tau _{\delta _c,{\bar{r}}}\) :
-
Compact set with suitable local covering
- \(K^{\tau ,\pm }\) :
-
Compact sets where the untangling functionals are controlled
- \({\mathcal {K}}^{n}\) :
-
Compact subset of \(\varGamma \) of trajectories with existence interval \(\ge 2^{1-n}\)
- \(Q^\ell _\gamma \) :
-
Cylinders of approximate flow
- \(\varphi \) :
-
Convolution kernel
- \(\varpi \) :
-
Constant controlling the flux across the lateral boundary of approximate cylinders of flows
- \(x_{{\mathbf {n}}}\) :
-
Coordinate along \({\mathbf {n}}\)
- \(x_{{\mathbf {n}}}^\perp \) :
-
Coordinates orthogonal to \({\mathbf {n}}\)
- \(\mathrm{dist}(x, E)\) :
-
Distance of the point \(x \in X\) from the set \(E \subset X\) in a metric space X
- \(C_d\) :
-
Dimensional constant
- \(D_{\mathbf {e}} f\) :
-
Directional derivative of f along \({\mathbf {e}}\)
- \(\delta _x\) :
-
Dirac mass at x
- \(D f\) :
-
Differential of the function f
- \(\mu = \int \mu _\alpha \, f_\sharp \mu (d\alpha )\) :
-
Disintegration of \(\mu \) w.r.t. the partition \(\{A_\alpha \}_\alpha \)
- \({{\,\mathrm{div}\,}}{\mathbf {b}}\) :
-
Divergence of the vector field \({\mathbf {b}}\)
- \({\mathcal {H}}^d\) :
-
d-Dimensional Hausdorff measure
- \(\langle f,\psi \rangle \) :
-
Distribution f evaluated on \(\psi \)
- \(\textsf {m} \) :
-
Direction of the variation in the rank-one property
- \(\overline{\textsf {m} }\) :
-
Direction of the variation in the rank-one property at the point \((\bar{t},{\bar{x}})\)
- \(\texttt {M} \) :
-
Deformation factor
- \(\mu ^\beta _\mathfrak {a}\) :
-
Disintegration of the measure \({{\,\mathrm{div}\,}}(\beta (\rho ) (1,\mathbf {b}))\)
- \(\mathbb {R}^d\) :
-
d-Dimensional real vector space
- \(\textsf {Tr} ^{{\mathrm {in}}}(B, \Omega ) \cdot \mathbf {n}\) :
-
Distributional inner normal trace
- \(\textsf {Tr} ^{{\mathrm {out}}}(B, \Omega ) \cdot \mathbf {n}\) :
-
Distributional outer normal trace
- \(w_\mathfrak {a}(t)\) :
-
Density of the disintegration of \({\mathcal {L}}^{d+1}\) w.r.t. \(\{\wp _\mathfrak {a}\}_\mathfrak {a}\)
- \(\mathbf {b}_t\) :
-
Equivalent to \(\mathbf {b}(t)\) for time dependent vector fields
- \(E_\mathfrak {a}\) :
-
Equivalence classes of \(\sim \)
- \(\ell ^\pm _{1,\gamma }\) :
-
Evolution of the \({\mathbf {e}}_1\)-boundary of the approximate cylinder
- \(\gamma \sim \gamma '\) :
-
Equivalent relation among untangled trajectories
- \(\rho ^i_\Omega \) :
-
Evaluation of the measure \(\eta ^i_\Omega \)
- \(\sigma (f(t))\) :
-
Evaluation of the function f w.r.t. the measure \(\rho (t) {\mathcal {L}}^d\)
- \(t^{i,-}_\gamma \) :
-
Entrance time of \(\gamma \) in \(\Omega \)
- \(t^{i,+}_\gamma \) :
-
Exit time of \(\gamma \) in \(\Omega \)
- \(\wp _\mathfrak {a}\) :
-
Evaluation of the equivalence class \(E_\mathfrak {a}\)
- \(\Phi ^{\ell }_{{\mathrm {enter}}}(\gamma )\) :
-
Functional computing intersecting curves across \(\phi ^\ell _\gamma \)
- \(\Phi ^{\ell }_{{\mathrm {exit}}}(\gamma )\) :
-
Functional computing the curves exiting the cylinder \(\phi ^\ell _\gamma \)
- \(I_{2,\gamma }\) :
-
Flow across \(L_{2,\gamma }\)
- \(I^-_{1,\gamma }\) :
-
Flow across \(L^-_{1,\gamma }\)
- \(I^+_{1,\gamma }\) :
-
Flow across \(L^+_{1,\gamma }\)
- \(t^+_\gamma \) :
-
Final time of the interval \(I_\gamma \)
- \({\mathcal {U}}\) :
-
Function locally approximating \(\mathbf {b}\)
- \(A\) :
-
Generic set
- \(B\) :
-
Generic vector field in \(\mathbb {R}^{d+1}\)
- \(C\) :
-
Generic constant
- \({{\,\mathrm{Graph}\,}}f\) :
-
Graph of the function f
- \({{\,\mathrm{Graph}\,}}\gamma \) :
-
Graph of the a.c. curve \(\gamma \) in the closed interval of definition
- \(\mu \) :
-
Generic signed Radon measure
- \(\Omega \) :
-
Generic open set
- \(X\) :
-
Generic metric space
- \(\texttt {T} \) :
-
Hitting point map
- \(\phi ^{\delta ,\pm }\) :
-
Inner/outer distance functions from a set
- \({\mathrm {id}}\) :
-
Identity function
- \(I_\gamma = (t^-_\gamma ,t^+_\gamma )\) :
-
Interval of definition of the curve \(\gamma \)
- \({{\,\mathrm{int}\,}}A\) :
-
Interior of the set A
- \(\int f \, dx\) :
-
Integral of a Borel function f w.r.t. \({\mathcal {L}}^d\)
- \(\int f \, \mu \) :
-
Integral of a Borel function f w.r.t. \(\mu \)
- \(\texttt {R} ^i_\Omega \) :
-
ith restriction operator
- \(t^-_\gamma \) :
-
Initial time of the interval \(I_\gamma \)
- \(\textsf {Tr} ^{\mathrm {in}}({\mathbf {b}},\Omega )\) :
-
Inner trace of the vector fields \(\mathbf {b}\)
- \(D^{\mathrm {jump}}\mathbf {b}\) :
-
Jump part of \(D^{\mathrm {sing}}f\)
- \(\eta \) :
-
Lagrangian representation
- \({\tilde{\eta }}\) :
-
Lagrangian representation of \(\rho (1,\mathbf {b}) \llcorner _\Omega \), only used in Sect. 7
- \({\bar{L}}_{2}\) :
-
Lateral boundary of \({\bar{Q}}\) with normal \({\mathbf {e}}^\perp _1\)
- \(L_{2,\gamma }\) :
-
Lateral boundary of \(Q_{\ell ^\pm _{1,\gamma },\ell }\) with normal \({\mathbf {e}}^\perp _1\)
- \({\mathcal {L}}^d\) :
-
Lebesgue measure in \({\mathbb {R}^d}\)
- \(L_{1,\gamma }^\pm \) :
-
Lateral boundary of \(Q_{\ell ^\pm _{1,\gamma },\ell }\) given by the graph of \(\ell ^\pm _{1,\gamma }\)
- \(\partial ^l Q\) :
-
Lateral boundary of the set Q
- \(u\) :
-
\(L^\infty \)-solution to \({{\,\mathrm{div}\,}}(u\rho (1,\mathbf {b})) \in {\mathcal {M}}\)
- \(\varsigma _x\) :
-
Local representation of a Lipschitz boundary
- \(\delta _1\) :
-
Maximal shrinking coefficient of an approximate cylinder of flow
- \(\mu ^\beta \) :
-
Measure \({{\,\mathrm{div}\,}}(\beta (\rho ) (1,\mathbf {b}))\)
- \(M(x)\) :
-
Matrix derivative of the absolutely continuous part of a \({{\,\mathrm{BV}\,}}\) vector field
- \(\texttt {T} ^{i,\pm }_\Omega \) :
-
Mapping of \(\gamma \) to its \(\Omega \) entering/exiting point
- \(\varpi ^\tau \) :
-
Measure controlling the untangling functional
- \(\zeta _C^\tau \) :
-
Measure locally controlling the untangling functionals
- \({\mathcal {O}}(f)\) :
-
Notation for constant of the order f
- \(N\) :
-
Negligible set w.r.t. some measure
- \(\textsf {n} \) :
-
Normal to the rank-one property
- \(\overline{\textsf {n} }\) :
-
Normal to the rank-one property at the point \((\bar{t},{\bar{x}})\)
- \(\Vert \cdot \Vert \) :
-
Norm in a generic Banach space
- \(|\cdot |\) :
-
Norm in \(\mathbb {R}^d\)
- \(o(f)\) :
-
Notation for constant infinitesimal w.r.t. f
- \(U_\texttt {x} \) :
-
Neighborhood of \(\texttt {x} \)
- \(\mathbf {n}\) :
-
Outer unit normal to the \(\rho (1,\mathbf {b})\)-proper set \(\Omega \subseteq \mathbb {R}^{d+1}\)
- \(\nu ^\perp \) :
-
Orthogonal component of \(\nu \) w.r.t. to another given measure
- \(\mu \perp \nu \) :
-
Orthogonal measures
- \(\eta ^i_\Omega \) :
-
Push forward of \(\eta \) by \(\texttt {R} ^i_\Omega \)
- \(\phi \) :
-
Particular functions used in the paper, usually with an index/apex
- \(f_\sharp \mu \) :
-
Push-forward of the measure \(\mu \) through f
- \(K^n\) :
-
Projection of \({\mathcal {K}}^n\)
- \(\Omega ^\varepsilon \) :
-
Perturbation of a proper set constructed in Theorem 4.18
- \(\texttt {p} _X\) :
-
Projection on the space X
- \(\rho \) :
-
Positive solution to transport equation
- \((\texttt {R} _\Omega )_\sharp \eta \) :
-
Push forward of \(\eta \) by the multivalued map \(R_\Omega \)
- \(S_2\) :
-
Partition of the set \(\partial (\Omega ^\varepsilon \setminus \Omega )\), Theorem 4.18
- \(S_3^-\) :
-
Partition of the set \(\partial (\Omega ^\varepsilon \setminus \Omega )\), Theorem 4.18
- \(S_3^+\) :
-
Partition of the set \(\partial (\Omega ^\varepsilon \setminus \Omega )\), Theorem 4.18
- \(S_4\) :
-
Partition of the set \(\partial (\Omega ^\varepsilon \setminus \Omega )\), Theorem 4.18
- \(\varUpsilon \) :
-
Product space of intervals in \(\mathbb {R}\) and curves in \(\mathbb {R}^d\)
- \(\hat{\texttt {f} }\) :
-
Quotient map for \(\{E_\mathfrak {a}\}_\mathfrak {a}\)
- \(\texttt {f} \) :
-
Quotient map for \(\{\wp _\mathfrak {a}\}_\mathfrak {a}\)
- \({{\,\mathrm{Fr}\,}}(A,B)\) :
-
Relative boundary of A in B
- \({{\,\mathrm{clos}\,}}(A,B)\) :
-
Relative closure of the set A in B
- \({\tilde{\eta }}^{\mathrm {cr}}\) :
-
Restriction of \({\tilde{\eta }}\) to \(\varGamma ^{\mathrm {Cr}}\)
- \(\eta ^\varXi \) :
-
Restriction of \(\eta \) to \(\varXi \)
- \(f \llcorner _A\) :
-
Restriction of the function f to the set A
- \(f^r_x\) :
-
Rescaled f about \(x \in \mathbb {R}^d\)
- \(f({\bar{x}}\pm )\) :
-
Right left limit of a 1d function at \({\bar{x}}\)
- \({{\,\mathrm{int}\,}}(A,B)\) :
-
Relative interior of the set A in B
- \(\mu ^r_x\) :
-
Rescaled \(\mu \) about \(x \in \mathbb {R}^d\)
- \(\mu \llcorner _A\) :
-
Restriction of the measure \(\mu \) to the set A
- \(\partial ^\star F\) :
-
Reduced boundary of the set of finite perimeter F
- \(\frac{d\nu }{d\mu }\) :
-
Radon–Nikodym derivative of \(\nu \) w.r.t. \(\mu \ge 0\)
- \({\mathcal {R}}(f)\) :
-
Range of the function f
- \(\texttt {R} ^{0,\pm }_\Omega \) :
-
0th restriction operators
- \(\texttt {R} _\Omega \) :
-
Restriction operator
- \((\texttt {R} _\Omega )_\sharp \eta ^{{\mathrm {out}}}\) :
-
Restriction of \((\texttt {R} _\Omega )_\sharp \eta \) to the exiting trajectories
- \(C(X,Y)\) :
-
Space of continuous functions over X
- \(A \Subset B\) :
-
Set A whose compact closure is contained in B
- \({\textsf {Adm}}(\{\mu _i\}_{i \in I})\) :
-
Sets of admissible transference plans between the measures \(\mu _i\)
- \(A^{\ell }_{\gamma }\) :
-
Set of intersecting curves
- \(A^{\pm }\) :
-
Subset of \(\partial \Omega \) where trajectories are exiting or entering, respectively
- \(C^k(\mathbb {R}^d,\mathbb {R}^{d'})\) :
-
Space of functions on \(\mathbb {R}^d\) with continuous derivatives up to order k
- \(\mathscr {D}^\prime (\Omega )\) :
-
Space of distributions over the open set \(\Omega \subset \mathbb {R}^d\)
- \(D^{\mathrm {sing}}\mathbf {b}\) :
-
Singular part of Df
- \(E\mathbf {b}\) :
-
Symmetric part of the derivative \(D\mathbf {b}\)
- \(E^{\ell }_\gamma \) :
-
Set of curves not contained in \({{\,\mathrm{supp}\,}}\phi ^\ell _\gamma \)
- \({\bar{\ell }}_1\) :
-
Starting shape of the approximate cylinder of flow in the BV case
- \({\mathfrak {A}}\) :
-
Suitable set of indexes
- \(L\) :
-
Scale factor
- \(L^1(\mu ,Y)\) :
-
Space of functions whose modulus is \(\mu \)-integrable
- \(L^\infty (\mu ,Y)\) :
-
Space of functions with \(\mu \)-essentially bounded Y-norm
- \({\mathcal {M}}(X)\) :
-
Set of Radon measures
- \({\mathcal {S}}\) :
-
Sets of curves with the same initial point
- \({\mathcal {M}}_b(X)\) :
-
Set of bounded Radon measures
- \({\mathcal {M}}^+(X)\) :
-
Set of positive Radon measures
- \(\partial \Omega ^\varepsilon _1\) :
-
Subset of \(\partial \Omega \) defined in Theorem 4.18
- \(\partial \Omega ^\varepsilon _2\) :
-
Subset of \(\partial \Omega \) defined in Theorem 4.18
- \(\partial _{x_i} f\) :
-
Spatial partial derivative along the ith direction
- \(Q\) :
-
Sets of particular shape, with some index/apex
- \(S_1\) :
-
Subset of \(\partial (\Omega ^\varepsilon \setminus \Omega )\) defined in Theorem 4.18
- \({{\,\mathrm{supp}\,}}f\) :
-
Support of a function f
- \(\varDelta \) :
-
Set of untangled trajectories
- \(\varGamma \) :
-
Space of characteristics
- \(\varGamma ^{\mathrm {cr}}\) :
-
Set of trajectories crossing a domain
- \(\varGamma ^{\mathrm {cr}}(\Omega )\) :
-
Set of \(\Omega \)-crossing trajectories
- \(\varGamma ^{\mathrm {in}}(\Omega )\) :
-
Set of \(\Omega \)-entering trajectories
- \(\varXi \) :
-
Set of uniqueness of \(\eta \)
- \(W\) :
-
Set of trajectories with good intersection properties
- \(W_1\) :
-
Set of disjoint trajectories
- \(W_2\) :
-
Set of trajectories whose intersection is still a trajectory
- \(x\) :
-
Space coordinate
- \(|\mu |\) :
-
Total variation measure of \(\mu \)
- \(\partial _t f_t\) :
-
Time partial derivative
- \(\pi \) :
-
Transference plan
- \(\rho ^{\mathrm {cr}}\) :
-
(t, x)-evaluation of \(\eta ^{\mathrm {Cr}}\)
- \(t\) :
-
Time coordinate
- \(\mathring{W}\) :
-
Trajectories with good intersection properties in the open graph
- \(\mathbf {e}\) :
-
Unit vector
- \(E^f_h\) :
-
Upper level set of the function f
- \(E_h\) :
-
Upper level set of a function
-
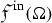 :
: -
Untangling functional for \(\eta ^{\mathrm {in}}\)
-
 :
: -
Untangling functional for \(\eta ^{\mathrm {out}}\)
- \({\mathbb {S}}^d\) :
-
Unit sphere of dimension d
- \(\mathbf {b} = (b_i)_{i=1}^d\) :
-
Vector
- \(\omega _d\) :
-
Volume of the unit ball in \(\mathbb {R}^d\)
- \(A(x)\) :
-
x section of \(A \subset X \times Y\)
Rights and permissions
About this article
Cite this article
Bianchini, S., Bonicatto, P. A uniqueness result for the decomposition of vector fields in \(\mathbb {R}^{{d}}\). Invent. math. 220, 255–393 (2020). https://doi.org/10.1007/s00222-019-00928-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-019-00928-8


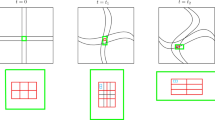
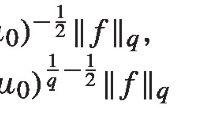

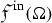 :
: :
: