Skip to main content

Advertisement

SpringerLink
Log in

Strong Isoperimetric Inequalities and Combinatorial Curvatures on Multiply Connected Planar Graphs

  • Published:
Discrete & Computational Geometry Aims and scope Submit manuscript

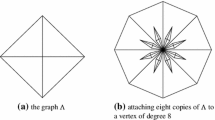
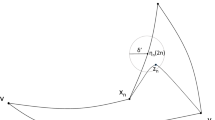
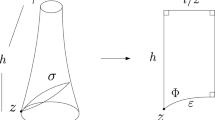
Abstract

The main focus of this paper is on hyperbolic properties of multiply connected planar graphs (planar graphs with multiple ends), and in the course we study some problematic phenomena of planar graphs caused by the existence of multiple (or sometimes infinite) ends. Specifically, in the first part of the paper we examine strong isoperimetric inequalities on a multiply connected planar graph G and its dual graph \(G^*\), and prove that G satisfies a strong isoperimetric inequality if and only if \(G^*\) has the same property, provided that G is either normal or finitely connected and we choose an appropriate notion for strong isoperimetric inequalities. In the second part we study a planar graph G on which negative curvatures uniformly dominate positive curvatures, and give a criterion that guarantees a strong isoperimetric inequality on G. Our criterion is useful in that it can be applied to a graph containing a long and slim subgraph with nonnegative combinatorial curvatures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Aleksandrov, A.D., Zalgaller, V.A.: Intrinsic Geometry of Surfaces, vol. 15. AMS Translations of Mathematical Monographs, Providence, RI (1967)

    MATH  Google Scholar 

  2. Baues, O., Peyerimhoff, N.: Curvature and geometry of tessellating plane graphs. Discrete Comput. Geom. 25(1), 141–159 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  3. Baues, O., Peyerimhoff, N.: Geodesics in non-positively curved plane tessellations. Adv. Geom. 6(2), 243–263 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  4. Benjamini, I., Schramm, O.: Every graph with a positive Cheeger constant contains a tree with a positive Cheeger constant. Geom. Funct. Anal. 7(3), 403–419 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  5. Biggs, N., Mohar, B., Shawe-Taylor, J.: The spectral radius of infinite graphs. Bull. Lond. Math. Soc. 20(2), 116–120 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bonk, M., Eremenko, A.: Uniformly hyperbolic surfaces. Indiana Univ. Math. J. 49(1), 61–80 (2000)

    MATH  MathSciNet  Google Scholar 

  7. Cheeger, J.: A Lower Bound for the Smallest Eigenvalue of the Laplacian. Problems in Analysis. Princeton University Press, Princeton (1970)

    MATH  Google Scholar 

  8. Corson, J.: Conformally nonspherical 2-complexes. Math. Z. 214(3), 511–519 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  9. de la Harpe, P.: Topics in Geometric Group Theory. Chicago Lectures in Mathematics. University of Chicago Press, Chicago (2000)

  10. DeVos, M., Mohar, B.: An analogue of the Descartes–Euler formula for infinite graphs and Higuchi’s conjecture. Trans. Am. Math. Soc. 359(7), 3287–3300 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  11. Diestel, R.: Graph Theory, 3rd edn. Graduate Texts in Mathematics, vol. 173. Springer, Berlin (2005)

  12. Diestel, R., Kühn, D.: Graph-theoretical versus topological ends of graphs. J. Comb. Theory Ser. B 87(1), 197–206 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  13. Dodziuk, J.: Difference equations, isoperimetric inequalities and transience of certain random walks. Trans. Am. Math. Soc. 284(2), 787–794 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  14. Dodziuk, J., Kendall, W.: Combinatorial Laplacians and isoperimetric inequality. In: Elworthy, K.D. (ed.) From Local Times to Global Geometry, Control and Physics (Coventry, 1984/1985), vol. 150, pp. 68–74. Pitman Research Notes in Mathematics Series. Longman Scientific and Technical, Harlow (1986)

  15. Fujiwara, K.: The Laplacian on rapidly branching trees. Duke Math. J. 83(1), 191–202 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  16. Gerl, P.: Random walks on graphs with a strong isoperimetric property. J. Theor. Probab. 1(2), 171–187 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  17. Ghys, E., de la Harpe, P. (eds.): Sur les Groupes Hyperbolique d’après Mikhael Gromov. Birkhäuser, Boston (1990)

  18. Gromov, M.: Hyperbolic groups. In: Gersten, S. (ed.) Essays in Group Theory, pp. 75–263. MSRI Publication 8. Springer, New York (1987)

  19. He, Z., Schramm, O.: Hyperbolic and parabolic packings. Discrete Comput. Geom. 14(2), 123–149 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  20. Higuchi, Y.: Combinatorial curvature for planar graphs. J. Graph Theory 38(4), 220–229 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  21. Higuchi, Y., Shirai, T.: Isoperimetric constants of \((d, f)\)-regular planar graphs. Interdiscip. Inf. Sci. 9(2), 221–228 (2003)

    MATH  MathSciNet  Google Scholar 

  22. Jendrol’, S., Voss, H.-J.: Light subgraphs of graphs embedded in the plane–a survey. Discrete Math. 313(4), 406–421 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  23. Keller, M.: The essential spectrum of the Laplacian on rapidly branching tessellations. Math. Ann. 346(1), 51–66 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  24. Keller, M.: Curvature, geometry and spectral properties of planar graphs. Discrete Comput. Geom. 46(3), 500–525 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  25. Keller, M., Peyerimhoff, N.: Cheeger constants, growth and spectrum of locally tessellating planar graphs. Math. Z. 268(3–4), 871–886 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  26. Lawrencenko, S., Plummer, M., Zha, X.: Isoperimetric constants of infinite plane graphs. Discrete Comput. Geom. 28(3), 313–330 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  27. Mohar, B.: Embeddings of infinite graphs. J. Comb. Theory Ser. B 44(1), 29–43 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  28. Mohar, B.: Isoperimetric numbers and spectral radius of some infinite planar graphs. Math. Slovaca 42, 411–425 (1992)

    MATH  MathSciNet  Google Scholar 

  29. Oh, B.: Aleksandrov surfaces and hyperbolicity. Trans. Am. Math. Soc. 357(11), 4555–4577 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  30. Oh, B.: Duality properties of strong isoperimetric inequalities on a planar graph and combinatorial curvatures. Discrete Comput. Geom. 51(4), 859–884 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  31. Oh, B.: Conformal and cp types of surfaces of class \({\cal S}\). Proc. Am. Math. Soc. 143(7), 2935–2947 (2015)

    Article  MATH  MathSciNet  Google Scholar 

  32. Reshetnyak, Yu G.: Two-dimensional manifolds of bounded curvature. In: Reshetnyak, Yu G. (ed.) Geometry IV. Encyclopaedia of Mathematical Sciences, vol. 70, pp. 3–163. Springer, Berlin (1993)

    Google Scholar 

  33. Soardi, P.: Recurrence and transience of the edge graph of a tiling of the Euclidean plane. Math. Ann. 287(4), 613–626 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  34. Soardi, P.: Potential Theory on Infinite Networks. LNM 1590. Springer, Berlin (1994)

    Book  Google Scholar 

  35. Stone, D.: A combinatorial analogue of a theorem of Myers. Ill. J. Math. 20(1), 12–21 (1976)

    MATH  MathSciNet  Google Scholar 

  36. Woess, W.: A note on tilings and strong isoperimetric inequality. Math. Proc. Camb. Philos. Soc. 124(3), 385–393 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  37. Woess, W.: Random Walks on Infinite Graphs and Groups. Cambridge Tracts in Mathematics, vol. 138. Cambridge University Press, Cambridge (2000)

  38. Żuk, A.: On the norms of the random walks on planar graphs. Ann. Inst. Fourier (Grenoble) 47(5), 1463–1490 (1997)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors deeply appreciate the anonymous referees for their helpful comments and suggestions, which helped to improve the presentation of this paper in many aspects. This paper was revised while B. Oh was visiting Korea Institute for Advanced Study (KIAS) in 2016. He thanks KIAS for warm hospitality. B. Oh was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (2010-0004113).

Author information

Authors and Affiliations

  1. Department of Mathematics Education, Hanyang University, 222 Wangsimni-ro, Seongdong-gu, Seoul, 04763, Korea

    Byung-Geun Oh

  2. Department of Mathematics, Soongsil University, 369 Sangdo-Ro, Dongjak-Gu, Seoul, 06978, Korea

    Jeehyeon Seo

Authors
  1. Byung-Geun Oh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jeehyeon Seo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Byung-Geun Oh.

Additional information

Editor in Charge: János Pach

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Oh, BG., Seo, J. Strong Isoperimetric Inequalities and Combinatorial Curvatures on Multiply Connected Planar Graphs. Discrete Comput Geom 56, 558–591 (2016). https://doi.org/10.1007/s00454-016-9805-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00454-016-9805-3

Keywords

Mathematics Subject Classification

Search

Navigation