A quasi-continuum multi-scale theory for self-diffusion and fluid ordering in nanochannel flows

Abstract

We present a quasi-continuum self-diffusion theory that can capture the ordering effects and the density variations that are predicted by non-equilibrium molecular dynamics (NEMD) in nanochannel flows. A number of properties that affect fluid ordering in NEMD simulations are extracted and compared with the quasi-continuum predictions. The proposed diffusion equation requires the classic diffusion coefficient D and a micro structural internal length g that relates directly to the shape of the molecular potential of the NEMD calculations. The quasi-continuum self-diffusion theory comes as an alternative to atomistic simulation, bridging the gap between continuum and atomistic behavior with classical hydrodynamic relations and reduces the computational burden as compared with fully atomistic simulations.

Appendices

Appendix 1: ODE solution for the 1D state problem

The general solution of Eq. (30) is

$$c(z) = A_{1} + A_{2} z + A_{3} \sin \frac{z}{g} + A_{4} \cos \frac{z}{g}$$

(46)

where A ₁, …A ₄ are constants to be determined by BC. The first two terms are similar to the classic solution. The other two terms are the non-classic part of the solution. Taking the region 0 ≤ z ≤ h _ch, (h _ch is the channel width), we impose the following BCs that are compatible with the Poiseuille flow in the normal to z-direction.

$$J = - D\left( {\frac{{{\text{d}}c}}{{{\text{d}}z}} + g^{2} \frac{{{\text{d}}^{3} c}}{{{\text{d}}z^{3} }}} \right)$$

(47)

At z = 0 and h _ch, J = 0, that is no flux at the walls, which gives

$$A_{2} = 0$$

(48)

At z = h _ch/2, c = c _o a datum point at the middle of the channel (can be thought of as a constant that increases with temperature), which gives

$$A_{1} = c_{o} - A_{3} \sin \frac{{h_{\text{ch}} }}{2g} - A_{4} \cos \frac{{h_{\text{ch}} }}{2g},c_{o} \ge 0$$

(49)

Symmetry of the concentration implies dc/dz = 0 at z = h _ch/2, which gives

$$A_{3} \cos \frac{{h_{\text{ch}} }}{2g} = A_{4} \sin \frac{{h_{\text{ch}} }}{2g}$$

(50)

This condition implies that J = 0 at z = h _ch, as expected. It can be shown that J = 0 for all z, 0 ≤ z ≤ h _ch.

Mass conservation implies

$$\int\limits_{0}^{{h_{\text{ch}} /2}} {c(z){\text{d}}z} = \bar{c}\frac{{h_{\text{ch}} }}{2},\quad\bar{c} > 0$$

(51)

which gives

$$A_{1} + A_{4} \frac{2g}{{h_{\text{ch}} }}\sin \frac{{h_{\text{ch}} }}{2g} + A_{3} \frac{2g}{{h_{\text{ch}} }}\left( {1 - \cos \frac{{h_{\text{ch}} }}{2g}} \right) = \bar{c}$$

(52)

Solving Eqs. (49), (50) and (52), we obtain

$$A_{4} = (c_{o} - A_{1} )\cos \frac{{h_{\text{ch}} }}{2g}$$

(53)

$$A_{3} = (c_{o} - A_{1} )\sin \frac{{h_{\text{ch}} }}{2g}$$

(54)

$$A_{1} = c_{o} \frac{{\frac{{\bar{c}}}{{c_{o} }} - \frac{2g}{{h_{\text{ch}} }}\sin \frac{{h_{\text{ch}} }}{2g}}}{{1 - \frac{2g}{{h_{\text{ch}} }}\sin \frac{{h_{\text{ch}} }}{2g}}}$$

(55)

For $\bar{c} = c_{o}$, we obtain the classic relation c = c _o .

Appendix 2: Asymptotic analysis

The solution of Eq. (37) can be written as combinations of hypergeometric function ₁ F ₁ and the Hermitian polynomial H:

$$\frac{{{\text{d}}^{2} c}}{{{\text{d}}z^{2} }} = e^{{ - \frac{{Az^{2} }}{{2g_{0} }}}} \left\{ {c_{1} H\left( {\frac{{1 - Ag_{o} }}{{2Ag_{o} }},\frac{\sqrt A z}{{\sqrt {g_{o} } }}} \right) + c_{2} \,\,{}_{1}F_{1} \left( {\frac{{ - 1 + Ag_{o} }}{{4Ag_{o} }};\frac{1}{2};\frac{{Az^{2} }}{{g_{o} }}} \right)} \right\}$$

(56)

where c ₁ and c ₂ are real constants. Note that only the hypergeometric function ₁ F ₁ is symmetric with respect to z. Therefore, symmetric cases are accepted only if c ₁ = 0. An interesting expansion of the solution around z = 0 (middle of the channel) is given below. In some cases in the field of heat transfer, the variational iteration method is utilized as an approximate analytical method to overcome some inherent limitations arising as uncontrollability to the nonzero endpoint boundary conditions (see, for example, Fouladi et al. 2010).

It is of interest to expand the symmetric solution (c ₁ = 0) around point z = 0 (the middle of the channel width).

$$\begin{aligned} \frac{{{\text{d}}^{2} c}}{{{\text{d}}z^{2} }} & = e^{{ - \frac{{Az^{2} }}{{2g_{o} }}}} c_{2} {}_{1}F_{1} \left( {\frac{{ - 1 + Ag_{o} }}{{24g_{o} }};\frac{ 1}{ 2};\frac{{Az^{2} }}{{g_{o} }}} \right) \\ & \quad \approx c_{2} \left\{ {1 - \frac{{z^{2} }}{{2g_{o}^{2} }} + \left( {\frac{1}{{24g_{o}^{4} }} + \frac{{A^{2} }}{{12g_{o}^{2} }}} \right)z^{4} - \left( {\frac{1}{{720g_{o}^{6} }} + \frac{{7A^{2} }}{{360g_{o}^{2} }}} \right)z^{6} + 0\left( {z^{8} } \right)} \right\} \\ \end{aligned}$$

(57)

Note that the expansion (57) involves only even powers of z. Taking the conditions dc/dz = 0 and c = c _o at z = 0, and retaining the first two terms of (57), we obtain

$$\frac{{{\text{d}}c}}{{{\text{d}}x}} \approx c_{2} \left( {z - \frac{{z^{3} }}{{6g_{o}^{2} }}} \right) + 0\left( {z^{5} } \right)$$

(58)

and

$$c \approx c_{o} + c_{2} \left( {\frac{{z^{2} }}{2} - \frac{{z^{4} }}{{24g_{o}^{2} }}} \right) + 0\left( {z^{6} } \right)$$

(59)

Assuming that (59) should provide c ≥ 0 for all values of c _o  ≥ 0, we conclude that c ₂ ≥ 0. In other words, dc ²/dz ² ≥ 0 at z = 0, a result that is verified by the NEMD calculations!

Appendix 3: Diffusion for asymmetric wall conditions

The case of asymmetric wall conditions can be studied by a diffusion inhomogeneous distribution of the type

$$D = D_{o} (1 - Bz/g_{o} )$$

(60)

The diffusion equation becomes

$$\frac{{d^{4} c}}{{{\text{d}}z^{4} }} + \frac{{(1 - Bz/g_{o} )}}{{g_{o}^{2} }}\frac{{d^{2} c}}{{{\text{d}}z^{2} }} = 0$$

(61)

The solution of Eq. (61) can be put in closed form.

$$\frac{{d^{2} c}}{{{\text{d}}z^{2} }} = c_{2} A_{i} \left[ {\frac{{ - 1 + Bz/g_{o} }}{{B^{2/3} }}} \right] + c_{3} B_{i} \left[ {\frac{{ - 1 + Bz/g_{o} }}{{B^{2/3} }}} \right]$$

(62)

where A _i and B _i are Airy functions and c ₂, c ₃ are constants. The full solution of Eq. (62) is given by

$$c(z) = c_{o} + c_{1} z + c_{2} C_{\rm A} (z) + c_{3} C_{\rm B} (z)$$

(63)

where c _o , c ₁, c ₂, c ₃ are constants.

The general form of the functions C _A(z) and C _B(z)are

$$\begin{aligned} C_{A} (z) & = \frac{1}{{3^{11/3} \varGamma \left( \frac{4}{3} \right)\varGamma \left( \frac{5}{3} \right)}}\left\{ {3\left( { - \frac{{g_{o} }}{B} + z} \right)^{2} \varGamma \left( \frac{1}{3} \right){}_{p}F_{q} \left[ {\left\{ \frac{1}{3} \right\},\left\{ {\frac{4}{3},\frac{5}{3}} \right\},\frac{{B\left( { - \frac{{g_{o} }}{B} + z} \right)^{2} }}{{9g_{o}^{2} }}} \right]} \right. \\ & \quad - \frac{1}{B}\left[ {3^{1/3} \left( {\frac{B}{{g_{o}^{3} }}} \right)^{1/3} \varGamma \left( \frac{2}{3} \right)} \right.\left[ {6{\text{g}}_{\text{o}}^{ 2} - 3^{1/3} 2g_{\text{o}}^{ 2} \left( {\frac{{\sqrt B \left( { - \frac{2}{B} + z} \right)^{3/2} }}{{g_{o}^{3/2} }}} \right)^{2/3} I\left[ { - \frac{2}{3},\frac{{2\sqrt B \left( { - \frac{{g_{o} }}{B} + z} \right)^{3/2} }}{{3g_{o}^{3/2} }}} \right]\varGamma \left( \frac{1}{3} \right)} \right. \\ & \quad + 3B\left( { - \frac{{g_{o} }}{B} + z} \right)^{3} {}_{p}F_{q} \left. {\left. {\left. {\left[ {\left\{ \frac{2}{3} \right\},\left\{ {\frac{4}{3},\frac{5}{3}} \right\},\frac{{B\left( { - \frac{{g_{o} }}{B} + z} \right)^{2} }}{{9g_{o}^{2} }}} \right]} \right]} \right]} \right\} \\ \end{aligned}$$

(64)

$$\begin{aligned} C_{B} (z) & = \frac{1}{{3^{17/6} \varGamma \left( \frac{4}{3} \right)\varGamma \left( \frac{5}{3} \right)}}\left\{ {3^{2/3} \left( { - \frac{{g_{o} }}{B} + z} \right)^{2} \varGamma \left( \frac{1}{3} \right){}_{p}F_{q} \left[ {\left\{ \frac{1}{3} \right\},\left\{ {\frac{4}{3},\frac{5}{3}} \right\},\frac{{B\left( { - \frac{{g_{o} }}{B} + z} \right)^{2} }}{{9g_{o}^{3} }}} \right]} \right. \\ & \quad + \frac{1}{B}\left[ {\left( {\frac{B}{{g_{o}^{3} }}} \right)^{1/3} \varGamma \left( \frac{2}{3} \right)} \right.\left[ {6{\text{g}}_{o}^{2} - 3^{1/3} 2g_{o}^{2} \left( {\frac{{\sqrt B \left( { - \frac{{g_{o} }}{B} + z} \right)^{3/2} }}{{g_{o}^{3/2} }}} \right)^{2/3} I\left[ { - \frac{2}{3},\frac{{2\sqrt B \left( { - \frac{{g_{o} }}{B} + z} \right)^{3/2} }}{{3g_{o}^{3/2} }}} \right]\varGamma \left( \frac{1}{3} \right)} \right. \\ & \quad + 3B\left( { - \frac{{g_{o} }}{B} + z} \right)^{3} {}_{p}F_{q} \left. {\left. {\left. {\left[ {\left\{ \frac{2}{3} \right\},\left\{ {\frac{4}{3},\frac{5}{3}} \right\},\frac{{B\left( { - \frac{{g_{o} }}{B} + z} \right)^{3} }}{{9g_{o}^{3} }}} \right]} \right]} \right]} \right\} \\ \end{aligned}$$

(65)

_p F _q is the generalized hypergeometric function, I is the modified Bessel function of the first kind, Γ is the Gamma function, and B is a parameter of the problem.

We believe that the chemical affinity between the walls and the fluid, as well as the roughness of the walls, influence the diffusion coefficient distribution and this, in turn, affects the steady state concentration profiles.

Appendix 4: Temperature profile

Temperature is calculated in each bin across the channel using

$$T_{\text{bin}} = \frac{{m_{Ar} }}{{3N_{\text{bin}} k_{B} }}\sum\limits_{n - 1}^{{N_{\text{bin}} }} {\sum\limits_{i - 1}^{3} {\left( {v_{n ,i} - {\bar{\text{v}}}_{i} } \right)^{2} } }$$

(66)

where N _bin is the number of fluid atoms in the bin examined, i = 1, 2, 3, … denotes the x, y, z component of the atomic velocity $v_{n - 1}$, ${\bar{\text{v}}}_{\text{i}}$ is the ith component of the mean macroflow velocity, k _B is the Boltzman constant, and m _Ar is argon atom mass.

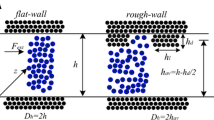
In Fig. 6a, the calculated fluid temperature distribution for h _ch = 6.3 nm is presented. We can see that for each system temperature (the temperature value imposed at the wall’s thermostats, 100, 120, or 150 K), the temperature profile is approximately flat at this temperature value. We obtain similar flat behavior when we vary system parameters such as channel width h _ch, the wall atoms spring constant K ^*, the wall–fluid interaction ratio ɛ _wall /ɛ _fluid an the average fluid density ρ ^*. However, in Fig. 6b, for h _ch = 17.1 nm and external forces above 0.036 pN, temperature profiles are not uniform and show a rise in the middle of the channel and near the solid walls. Similar behavior is reported on Nagayama and Cheng (2004) when the external force that drives the flow becomes large. We attribute this behavior to the fact that at large channel widths, in combination with external forces of large magnitude, strain rates inside the nanochannel increase, and the system has non-linear response.

Fig. 6

Temperature profiles a for system temperature T = 100, 120 and 150 K, and h _ch = 6.3 nm b for various magnitudes of the F _ext (normalized), T = 120 K and $h_{\text{ch}} = 17.1{\text{ nm}}$