Periodic Solutions of Piecewise Affine Gene Network Models with Non Uniform Decay Rates: The Case of a Negative Feedback Loop

Abstract

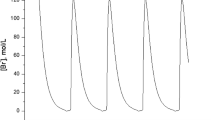
This paper concerns periodic solutions of a class of equations that model gene regulatory networks. Unlike the vast majority of previous studies, it is not assumed that all decay rates are identical. To handle this more general situation, we rely on monotonicity properties of these systems. Under an alternative assumption, it is shown that a classical fixed point theorem for monotone, concave operators can be applied to these systems. The required assumption is expressed in geometrical terms as an alignment condition on so-called focal points. As an application, we show the existence and uniqueness of a stable periodic orbit for negative feedback loop systems in dimension 3 or more, and of a unique stable equilibrium point in dimension 2. This extends a theorem of Snoussi, which showed the existence of these orbits only.

Appendix: Proofs

1.1 Proof that Local Maps Preserve Closed Walls

See Sect. 4.2.1 for notation.

Let $x\;{\in}\;c\ell({W^{i-1}})$ be such that x _j  = 0. Since $c\ell({W^{i-1}})\subset\{x | x_{s_{i-1}}=0\},$ we assume j ≠ s _i−1. Then, ${\mathcal T}^{a^i}x\;{\in}\;c\ell({W^{i}})$ if, and only if, each coordinate ${\mathcal T}^{a^i}_kx$ belongs to the projection of $c\ell({W^{i}})$ in the direction of k, which is either [0, θ ⁺ _k ] or [θ ⁻ _k , 0]. From (22), the coordinate map ${\mathcal T}^{a^i}_j\,$ depends only on variables x _j and x _s − i. Hence, there are two cases:

• If $j\neq s_i, {\mathcal T}^{a^i}_jx=(1-\alpha_j(x_s)) \phi_j^i$ depends on x _s only. From the inequalities linking x _j ,  ϕ ⁱ _j   and θ _j  = 0, it is easily checked that $\alpha_j(x_s) \in (0,1]$ for all x _s . From j ≠ s _i ,  ϕⁱ _j belongs to the projection of W ⁱ in direction j, hence so does the entire closed interval bounded by 0 and ϕⁱ _j , and in particular ${\mathcal T}^{a^i}_jx.$

• If j = s _i , then for any k ∈ {1…n}, $\alpha_{s_{k}}(x)=1$, so that ${\mathcal T}^{a^i}_kx=x_k,$ that is, x is a fixed point. Moreover, $x\,\in\,c\ell({W^{i-1}})\,\cap\,c\ell({W^{i}})$ in this case. Then ${\mathcal T}^{a^i}_kx=x_k$ clearly belongs to the projection of $c\ell({W^{i}})$ in the direction of k.

1.2 Proof of Proposition 4

Proof

From (17) and (18), it follows that sign(ϕ₁) = (− 1, 1…1) ∈ {± 1}ⁿ, so that σ¹ = (1…1) ∈ {± 1}^{2…n}, and

$$ {\mathcal Z}^1= \prod\limits_{j=2}^{n}[0, \phi_j^+], \quad \hbox {since }\phi_j^1=\phi_j^+\hbox { for }j\geq2. $$

Let $x^1 \in \widetilde W^1.$ In the following we denote $x^i = \widetilde{\mathcal T}^{a^{i}}x^{i-1}$ for $i \geq 2,$ so that ${\bf T} x^1 = x^{2n+1}.$ Clearly, $x^i \in \widetilde W^i$ for all i.

Now, for each i ∈ {1…2n}, the alignment condition (20) and the expression (22) of ${\mathcal T}^{a^i}$ imply the following conservation of signs:

$$ \forall i \in \{1 \ldots 2n\}, \forall j\neq s_{i+1},\quad \hbox{sign}\left(\phi^i_{j} - x^i_{j}\right) = \hbox{sign}\left(\phi^{i+1}_{j} - x^{i+1}_{j}\right). $$

In particular, for the n last domains of the cycle ${\mathcal C},$ remarking from Eq. 18 that s _n+i = i, the above has the following consequence:

$$ \forall i \in \{1\ldots n\}, \forall j < i+1,\quad \hbox{sign}\left(\phi^{n+i}_{j} - x^{n+i}_{j}\right) = \hbox{sign}\left(\phi^{n+i+1}_{j} - x^{n+i+1}_{j}\right). $$

This equality can be propagated, in the sense that

$$ \begin{aligned} \hbox{sign}\left(\phi^{n+1}_{1} - x^{n+1}_{1}\right) \,=\, & \hbox{sign}\left(\phi^{n+2}_{1} - x^{n+2}_{1}\right) =\,\cdots\,= \hbox{sign}(\phi^{2n}_{1} - x^{2n}_{1}) \,=\, \hbox{sign}(\phi^{1}_{1} - x^{2n+1}_{1}), \\ \hbox{sign}(\phi^{n+2}_{2} - x^{n+2}_{2}) \,=\, & \hbox{sign}(\phi^{n+3}_{2} - x^{n+3}_{2}) =\,\cdots\,= \hbox{sign}(\phi^{2n}_{2} - x^{2n}_{2}) = \hbox{sign}\left(\phi^{1}_{2} - x^{2n+1}_{2}\right),\\ \vdots & \\ \hbox{sign}\left(\phi^{2n-1}_{n-1} - x^{2n-1}_{n-1}\right) \,=\, & \hbox{sign}\left(\phi^{2n}_{n-1} - x^{2n}_{n-1}\right) = \hbox{sign}\left(\phi^{1}_{n-1} - x^{2n+1}_{n-1}\right) \\ \hbox{sign}\left(\phi^{2n}_{n} - x^{2n}_{n}\right) \,=\, & \hbox{sign}\left(\phi^{1}_{n} - x^{2n+1}_{n}\right) \end{aligned} $$

Now, since $x^{n+i} \in \widetilde W^{n+i},$ and since (23) is satisfied on $\widetilde W^{n+i}$ by definition, we obtain

$$ \hbox{sign}\left(\phi^{n+i+1}_{i} - x^{n+i+1}_{i}\right) = \hbox{sign}\left(\phi^{n+i+1}_{i}\right), \quad i \in \{1 \ldots n\}. $$

(38)

Combining this with the previous list of equalities gives

$$ \hbox{sign}\left(\phi^{1}_{i} - x^{2n+1}_{i}\right) = \hbox{sign}\left(\phi^{1}_{i}\right), \quad i \in \{1 \ldots n\}, $$

which means that $x^{2n+1}={\bf T} x^{1} \in {\mathcal Z}^1,$ as expected.$\square$

1.3 Proof of Proposition 5

Proof

Let $x \in {\mathcal Z}^i,$ which by definition is equivalent to

$$ \forall j \in \{1 \ldots n\} \setminus\{s_{i}\}, \quad \hbox{sign}\left(\phi_j^i - x_j\right) = \hbox{sign}\left(\phi_j^i\right). $$

(39)

First, observe that in dimension n = 2,  j = s _i−1 necessarily, and thus ${\mathcal Z}^i(\sigma^i)=\widetilde W^{i};$ see the discussion in Sect. 4.2.2. There is nothing to prove in this case, and we thus assume $n \geq 3$ in the rest of the proof.

From the alignment condition (20), we get

$$ \forall j\neq s_{i}, \quad \phi^{i}_j - \widetilde{\mathcal T}^{a^{i}}_jx = \left(\phi_j^{i-1}-x_j\right) \alpha_j(x). $$

Since α _j (x) > 0, using (39) leads to

$$ \forall j \in \{1\ldots n\} \setminus\{s_{i-1},s_i\}, \quad \hbox{sign}\left(\phi^{i}_j-\widetilde{\mathcal T}^{a^{i}}_jx\right) = \hbox{sign}\left(\phi_j^{i-1}\right) = \hbox{sign}(\phi_j^{i}). $$

From (23) it is immediate that

$$ \hbox{sign}\left(\phi^{i}_{s_{i-1}}-\widetilde{\mathcal T}^{a^{i}}_{s_{i-1}}x\right) = \hbox{sign}\left(\phi_{s_{i-1}}^{i-1}\right) = \hbox{sign}\left(\phi_{s_{i-1}}^{i}\right), $$

which concludes the proof.

$$ \square $$

1.4 Proof of Theorem 2: Last Part

Proof

The subscripts in (36) and (37) are those to be used in Eq. 33. To compute (35), on the other hand, it is more relevant to use the actual row and column numbers, as represented in (36) over the nonzero column, which is numbered s _i−1. Hence, in the expressions below, $D{\mathcal M}^{(i)}_{jk}$ refers to the entry j, k of matrix $D{\mathcal M}^{(i)}(0),$ which is not necessarily $\frac{\partial{\mathcal M}^{(i)}_j} {\partial x_k}(0).$ A simple induction shows that

$$ \left(D{\bf T}(x^1)\right)_{ij} = \sum_{k_1, \ldots, k_{2n-1}=1}^{n-1} D{\mathcal M}^{(1)}_{ik_1}D{\mathcal M}^{(2n)}_{k_1k_2}\,\cdots\,D{\mathcal M}^{(2)}_{k_{2n-1}j} $$

In particular, the diagonal terms can be conveniently denoted using the following abbreviation. Define the integer vector ${\bf k}=(k_1 \ldots k_{2n-1}) \in \{1 \ldots n-1\}^{2n-1},$ and denote

$$ p_{\bf k}^i = D{\mathcal M}^{(1)}_{ik_1}D{\mathcal M}^{(2n)}_{k_1k_2}\,\cdots\,D{\mathcal M}^{(2)}_{k_{2n-1}i}. $$

Note that the general form of terms in the products above is the following:

$$ D{\mathcal M}^{(j)}_{k_{2n+1-j}k_{2n+2-j}} \quad \quad j \in \{3 \ldots 2n\}. $$

Then, $\left(D{\bf T}(x^1)\right)_{ii}$ equals the sum of products $p_{\bf k}^i$ when k varies in the whole set {1…n − 1}²ⁿ⁻¹. Now, since each matrix $D{\mathcal M}^{(i)}(0)$ is composed of zeros and positive terms, it follows that each nonzero product $p_{\bf k}^i$ is positive. Hence, if for all i there is a k such that $p_{\bf k}^i=1,$ and at least one other nonzero $p_{\bf k}^i,$ the proof will be finished.

To help intuition, let us detail the shape of $D{\mathcal M}^{(i)}(0)$ and $D{\mathcal M}^{(n+i)}(0)$ for $n \geq i > 1,$ using (36) and (37):

$$ \begin{aligned} \begin{array}{c} \mathop{{i-1}}\limits_{\downarrow}\quad \,\,\qquad\qquad \\ \end{array} \\ \left[\begin{array}{ccccccc} 1 & & &|\kappa^i_1/\kappa^i_{i}| &&&\\ &\ddots&& \vdots&&&\\ &&1&|\kappa^i_{i-2}/\kappa^i_{i}|&&&\\ &&&|\kappa^i_{i-1}/\kappa^i_{i}|\\ &&&|\kappa^i_{i+1}/\kappa^i_{i}|&1&&\\ &&&\vdots&&\ddots&\\ &&& |\kappa^i_{n}/\kappa^i_{i}|&&&1\\ \end{array}\right] \end{aligned} $$

(40)

For i ∈ {1, n + 1}:

$$ D{\mathcal M}^{(i)}\equiv \left[\begin{array}{llll} |\kappa^i_2/\kappa^i_1| & 1 & & \\ \vdots & & \ddots & \\ \vdots & & & 1 \\ |\kappa^i_n/\kappa^i_1| & 0 &\,\cdots\,& 0 \end{array}\right] $$

(41)

Now, we claim that $p_{\bf k}^i=1,$ for 1 < i ≤ n − 1, and

$$ {\bf k}=(1 \ldots 1,i \ldots i,1 \ldots 1,i \ldots i) $$

(42)

where k _j  = i for n + 1 − i ≤ j ≤ n, and 2n + 1 − i ≤ j ≤ 2n − 1, and k _j  = 1 otherwise. Actually, we have, on the one hand,

$$ D{\mathcal M}^{(1)}_{i,k_1}=D{\mathcal M}^{(1)}_{i,1}=\left|\frac{\kappa^1_{i+1}} {\kappa^1_1}\right| \quad\hbox {and}\quad D{\mathcal M}^{(n+1)}_{k_n,k_{n+1}}=D{\mathcal M}^{(n+1)}_{i,1}=\left|\frac{\kappa^{n+1}_{i+1}} {\kappa^{n+1}_1}\right| $$

and, on the other hand,

$$ D{\mathcal M}^{(n+i+1)}_{k_{n-i},k_{n+1-i}}=D{\mathcal M}^{(n+i+1)}_{1,i}=\left|\frac {\kappa^{n+i+1}_1} {\kappa^{n+i+1}_{i+1}}\right| \quad \hbox {and} \quad D{\mathcal M}^{(i+1)}_{k_{2n-i},k_{2n+1-i}}=D{\mathcal M}^{(i+1)}_{1,i}=\left|\frac{\kappa^{i+1}_1} {\kappa^{i+1}_{i+1}}\right|. $$

Moreover, for any $j \in \{2n+1-i \ldots 2n-1\} \cup \{n+1-i \ldots n\},$ it appears that $D{\mathcal M}^{(j)}_{i,i}=1,$ since i ≠ s _j  − 1, and similarly, for $j \in \{1 \ldots n-i\} \cup \{n+1 \ldots 2n-i\},$ we have $D{\mathcal M}^{(j)}_{1,1}=1.$ As a consequence, for k as in (42),

$$ \begin{aligned} p_{\bf k}^i &= D{\mathcal M}^{(1)}_{i,1} D{\mathcal M}^{(n+i+1)}_{1,i} D{\mathcal M}^{(n+1)}_{i,1} D{\mathcal M}^{(i+1)}_{1,i}\\ &= \left|\frac{\kappa^1_{i+1}} {\kappa^1_1}\,\frac{\kappa^{n+i+1}_1} {\kappa^{n+i+1}_{i+1}} \,\frac{\kappa^{n+1}_{i+1}} {\kappa^{n+1}_1}\,\frac{\kappa^{i+1}_1} {\kappa^{i+1}_{i+1}}\right| \end{aligned} $$

(43)

Now we refer to the Eq. 17 of successive boxes, and recall that ϕⁱ belongs to the domain a ⁱ⁺¹. Then it is rather straightforward to check that

$$ \hbox{sign}\left(\phi^{n+i}\right)=-\hbox{sign}(\phi^i) $$

for any i ∈ {1…n}. It follows immediately that sign(κ^n + i) =  − sign(κⁱ) as well. From this and the fact that any production term κⁱ _j is fully determined by its sign, it follows that

$$ \frac{\kappa^{i+1}_1 \kappa^{n+i+1}_1} {\kappa^1_1\;\kappa^{n+1}_1}=1 \quad \hbox {and} \quad \frac{\kappa^1_{i+1} \kappa^{n+1}_{i+1}} {\kappa^{i+1}_{i+1} \kappa^{n+i+1}_{i+1}}=1, $$

whence $p_{\bf k}^i= 1.$

Recall that the previous holds only for i > 1. Now, let k = (1…1). Then,

$$ D{\mathcal M}^{(1)}_{1,k_1}=D{\mathcal M}^{(1)}_{1,1}=\left|\frac{\kappa^1_{2}} {\kappa^1_1}\right| \quad \hbox {and} \quad D{\mathcal M}^{(n+1)}_{k_n,k_{n+1}}=D{\mathcal M}^{(n+1)}_{1,1}=\left|\frac{\kappa^{n+1}_{2}} {\kappa^{n+1}_1}\right| $$

while

$$ D{\mathcal M}^{(n+2)}_{k_{n-1},k_{n}}=D{\mathcal M}^{(n+2)}_{1,1}=\left|\frac{\kappa^{n+2}_1} {\kappa^{n+2}_{2}}\right| \quad \hbox {and} \quad D{\mathcal M}^{(2)}_{k_{2n-1},1}=D{\mathcal M}^{(2)}_{1,1}=\left|\frac{\kappa^{2}_1} {\kappa^{2}_{2}}\right|. $$

Moreover, for any other $j, D{\mathcal M}^{(j)}_{1,1}=1,$ and thus

$$ \begin{aligned} p_{\bf k}^1 =\,& \left|\frac{\kappa^1_{2}} {\kappa^1_1} \frac{\kappa^{n+2}_1} {\kappa^{n+2}_{2}} \frac{\kappa^{n+1}_{2}} {\kappa^{n+1}_1}\frac{\kappa^{2}_1} {\kappa^{2}_{2}}\right| \\ =& \,1, \quad \quad \hbox {for the same reason as in (43)}. \end{aligned} $$

Thus, we have found, for each i ∈ {1…n − 1}, a k such that $p^i_{\bf k}=1.$ Now, for any i >  1, let ${\bf k}=(1 \ldots 1,i \ldots i),$ where k _j  = i for 2n + 1 − i ≤ j ≤ 2n − 1. This leads to

$$ p^i_{\bf k}=D{\mathcal M}^{(1)}_{i,1}D{\mathcal M}^{(2n)}_{1,1}\,\cdots\,D{\mathcal M}^{(i+1)}_{1,i}D{\mathcal M}^{(i)}_{i,i}\,\cdots\,D{\mathcal M}^{(2)}_{1,i}, $$

and from (40) and (41), we check readily that the above is positive: the entry (1, 1) is actually never zero in the first terms, the ith column of $D{\mathcal M}^{(i+1)}$ is nonzero, and the diagonal terms of the last terms in the product are positive as well.

For i = 1, a positive $p^1_{\bf k}$ is found for instance with k = (2…2). Actually, (2, 2) entries are never zero in (40), and moreover $D{\mathcal M}^{(1)}_{1,2}$ and $D{\mathcal M}^{(2)}_{2,1}$ are also positive.$\square$