Intrinsic Feedbacks in MAPK Signaling Cascades Lead to Bistability and Oscillations

Abstract

Previous studies have demonstrated that double phosphorylation of a protein can lead to bistability if some conditions are fulfilled. It was also shown that the signaling behavior of a covalent modification cycle can be quantitatively and, more importantly, qualitatively modified when this cycle is coupled to a signaling pathway as opposed to being isolated. This property was named retroactivity. These two results are studied together in this paper showing the existence of interesting phenomena—oscillations and bistability—in signaling cascades possessing at least one stage with a double-phosphorylation cycle as in MAPK cascades.

Appendices

Appendix 1: Simplified Kinetic Equations of the Double phosphorylation cascade

In this appendix we show how the 1-variable per cycle model (5)–(8) can be obtained from a singular perturbation analysis of the full mass-action kinetic equations. The procedure is standard, e.g. (Murray 2002).

According to the scheme in Eqs. (1), and using only the law of mass action, the dynamics of the i th cycle in a cascade of n cycles is governed by the conservation equations $Y_{{iT}} = Y_{i} + Y_{i}^{*} + Y_{i}^{{**}} + C_{{i1}} + C_{{i2}} + C_{{i1}}^{\prime } + C_{{i2}}^{\prime } + C_{{i + 1,1}} + C_{{i + 1,2}}$ and E ^′ _iT  = E ^′ _i  + C ^′ _i1  + C ^′ _i2 and by the following differential equations:

$$ \begin{aligned} \frac{d Y_i^{**} }{dt} &= k_{i2} C_{i2} - a_{i1}^{\prime} Y^{**}_i E_i^{\prime} + d_{i1}^{\prime} C_{i1}^{\prime} - a_{i+1,1} Y_{i+1} Y_{i}^{**} + (k_{i+1,1}+d_{i+1,1}) C_{i+1,1}\\ &\quad- a_{i+1,2} Y_{i+1}^{*} Y_{i}^{**} + (k_{i+1,2}+d_{i+1,2}) C_{i+1,2} \\ \frac{d Y_i}{dt} &= k_{i2}^{\prime} C_{i2}^{\prime} - a_{i1} Y_i Y^{**}_{i-1} + d_{i1} C_{i1} \\ \frac{d C_{i1} }{dt} &= a_{i1} Y_i Y_{i-1}^{**} - (k_{i1}+d_{i1}) C_{i1} \\ \frac{d C_{i2} }{dt} &= a_{i2} Y_i^* Y_{i-1}^{**} - (k_{i2}+d_{i2}) C_{i2} \\ \frac{d C_{i1}^{\prime} }{dt} & = a_{i1}^{\prime} Y_i^{**} E_i^{\prime} -(k_{i1}^{\prime}+d_{i1}^{\prime}) C_{i1}^{\prime}\\ \frac{d C_{i2}^{\prime} }{dt} &= a_{i2}^{\prime} Y_i^{*} E_i^{\prime} -(k_{i2}^{\prime}+d_{i2}^{\prime}) C_{i2}^{\prime} \end{aligned} $$

(20)

with $i = 1, \ldots n,$ with the convention that $Y_{0}^{{**}}$ is related to the input stimulus, whereas Y _n+1 = C _n+1, j  = 0 (j = 1,2).

As described in Sect. 2, we define the parameters ε _i  = E ^′ _iT / Y _iT and η _i  = Y _i-1,T /Y _iT . Michaelis constants are defined as usual as K _ij  = (k _ij  + d _ij )/a _ij and K ^′ _ij  = (k ^′ _ij  + d ^′ _ij )/a ^′ _ij . We define also new variables X _i  = Y ^** _i  + C _i+1,1 + C _i+1,2 that reveal to be natural slow variables of the system. The variables are turned into dimensionless ones in the following way:

$$ x_i = \frac{ X_i }{Y_{iT}}, \quad y_i = \frac{ Y_i }{ Y_{iT}}, \quad c_{ij}= \frac{ C_{ij} }{Y_{i-1,T}}, \quad c_{ij}^{\prime} = \frac{ C_{ij}^{\prime} }{E_{iT}^{\prime}}, \quad e_i^{\prime} = \frac{ E_i^{\prime} }{E_{iT}^{\prime}}. $$

(21)

The previous system of ODEs can be then written as:

$$ \frac{d x_i }{dt} = \eta_i k_{i2} c_{i2} - \epsilon_i k_{i1}^{\prime} c_{i1}^{\prime} - \epsilon_i a_{i1}^{\prime} Y_{iT} \left[ ( x_i-c_{i+1,1}-c_{i+1,2}) e_i^{\prime} - K_{i1}^{\prime} c_{i1}^{\prime} \right] $$

(22)

$$ \frac{d y_i }{dt} = \epsilon_i k_{i2}^{\prime} c_{i2}^{\prime} - \eta_i k_{i1} c_{i1} - \eta_i a_{i1} Y_{iT} \left[ y_i ( x_i-c_{i+1,1}-c_{i+1,2}) - K_{i1} c_{i1} \right] $$

(23)

$$ \frac{d c_{i1} }{dt} = a_{i1} Y_{iT} \left( y_i (x_{i-1} -c_{i1}-c_{i1}) - K_{i1} c_{i1} \right) $$

(24)

$$ \frac{d c_{i2} }{dt} = a_{i2} Y_{iT} \left( y^*_i (x_{i-1} -c_{i1}-c_{i1}) - K_{i2} c_{i2} \right) $$

(25)

$$ \frac{d c_{i1}^{\prime} }{dt} = a_{i1}^{\prime} Y_{iT} \left( (x_i-c_{i+1,1}-c_{i+1,2}) e_{i}^{\prime} - K_{i1}^{\prime} c_{i1}^{\prime} \right) $$

(26)

$$ \frac{d c_{i2}^{\prime} }{dt} = a_{i2}^{\prime} Y_{iT} \left( y^*_i e_{i}^{\prime} - K_{i2}^{\prime} c_{i2}^{\prime} \right) $$

(27)

with $i=1,\ldots,n,$ with again the convention that in these equations c _n+1,j  = 0, and x ₀ = S denotes the input stimulus (e.g. some available active enzyme) normalized by η₁ Y _1T . Here the conservation laws become $x_i + y^*_i + y_i + \eta_i (c_{i1} + c_{i2} ) + \epsilon_i ( c_{i1}^{\prime} + c_{i2}^{\prime}) = 1$ and $c_{i1}^{\prime} + c_{i2}^{\prime} + e_i^{\prime} = 1$.

Now, in the limit where all $\epsilon_i \rightarrow 0,$ and assuming that $k_{i1} \eta_i \sim k_{i2}^{\prime} \epsilon_i$ and $k_{i2} \eta_i \sim k_{i1}^{\prime} \epsilon_i,$ we get a slow dynamics for the variables x _i and y _i as compared with the rates of change of the complexes c _i and $c_i^{\prime},$ so that the quasi-steady state approximation can be applied. Let us assume that $\epsilon$ is a representative value of the set $\{ \epsilon_1, \epsilon_2, \cdots, \epsilon_n \}$ and consider a slow time-scale $\tilde{t} = \epsilon t$ with the time-derivative with respect to $\tilde{t}$ that is denoted by a dot, i.e. $\dot{x} = dx/d \tilde{t}$. By imposing that $\dot{c}_{ij} = \dot{c}_{ij}^{\prime} =0,$ a little calculation gives:

$$ \begin{aligned} c_{i1} &= x_{i-1} \frac{y_i/K_{i1}}{1+y_i/K_{i1}+y^*_i/K_{i2}} \\ c_{i2} &= x_{i-1} \frac{y^*_i/ K_{i2}}{1+y_i/ K_{i1}+y^*_i/ K_{i2}} \\ c_{i1}^{\prime} & = \frac{x_i/ K_{i1}^{\prime}}{(1+y_{i+1}/K_{i+1,1}+y^*_{i+1}/K_{i+1,2})(1+y^*_i/ K_{i2}^{\prime}) +x_i/ K_{i1}^{\prime}} \\ c_{i2}^{\prime} &= \frac{y^*_i/ K_{i2}^{\prime}}{1+y_i/ K_{i1}^{\prime}+y^*_i/ K_{i2}^{\prime}} \\ \end{aligned} $$

Finally, the substitution of these expressions in Eqs. (22) gives the new model Eqs. (5)–(8), with $V_{ij} = k_{ij} \eta_i / \epsilon$ and $V_{ij}^{\prime} = k_{ij}^{\prime} \epsilon_i / \epsilon$.

Appendix 2: Computation of the Interaction Graph

In this Appendix we prove inequalities (9) in order to show that in the interaction graph (Fig. 3) the variables at stage i + 1 of the cascade have a negative influence on the variables at stage i. This can be achieved by computing the corresponding elements of the Jacobian matrix as follows :

$$ \frac{\partial \dot{x}_i}{\partial x_{i+1}} = \frac{V_{i1}^{\prime} x_i}{(K_{eff,i1}^{\prime}+x_i)^2} \frac{K_{i1}^{\prime}\left(1+\frac{y_i^*}{K_{i2}^{\prime}}\right)}{K_{i+1,2}} \frac{\partial y_{i+1}^*}{\partial x_{i+1}} $$

(28)

$$ \frac{\partial \dot{x}_i}{\partial y_{i+1}} = \frac{V_{i1}^{\prime} x_i}{(K_{eff,i1}^{\prime}+x_i)^2} \frac{K_{i1}^{\prime}\left(1+\frac{y_i^*}{K_{i2}^{\prime}}\right)}{K_{i+1,2}} \frac{\partial y_{i+1}^*}{\partial y_{i+1}} $$

(29)

$$ \frac{\partial \dot{y}_i}{\partial x_{i+1}} = \frac{V^\prime_{i2} y_i^* }{(K_{eff,i2}^{\prime} + y_i^* )^2 } \frac{K_{i2}^\prime x_i }{ K_{i1}^\prime \left(\frac{y_{i+1}}{K_{i+1,1}}+\frac{y^*_{i+1}}{K_{i+1,2}}\right)^2 K_{i+1,2}} \frac{\partial y_{i+1}^*}{\partial x_{i+1}} $$

(30)

$$ \frac{\partial \dot{y}_i}{\partial y_{i+1}} = \frac{V^\prime_{i2} y_i^* }{(K_{eff,i2}^{\prime} + y_i^* )^2 } \frac{K_{i2}^\prime x_i }{ K_{i1}^\prime \left(\frac{y_{i+1}}{K_{i+1,1}}+\frac{y^*_{i+1}}{K_{i+1,2}}\right)^2 K_{i+1,2}} \frac{\partial y_{i+1}^*}{\partial y_{i+1}} $$

(31)

and the remaining partial derivatives can be computed by using the conservation law (7). These factors are always negative:

$$ \begin{aligned} \frac{\partial y_{i+1}^*}{\partial x_{i+1}} &= - \left( \frac{1}{1+\eta_{i+1} x_i \frac{1/K_{i+1,2}}{ (1+y_{i+1}/K_{i+1,1} + y_{i+1}^*/K_{i+1,2})^2}} \right) \\ \frac{\partial y_{i+1}^*}{\partial y_{i+1}} &= - \left( \frac{1+\eta_{i+1} x_i \frac{1/K_{i+1,1}}{ (1+y_{i+1}/K_{i+1,1} + y_{i+1}^*/K_{i+1,2})^2}}{1+\eta_{i+1} x_i \frac{1/K_{i+1,2}}{ (1+y_{i+1}/K_{i+1,1} + y_{i+1}^*/K_{i+1,2})^2}} \right) \end{aligned} $$

Appendix 3: Computation of the Steady-States for a 2-Stage Cascade

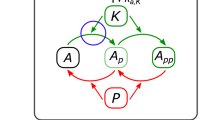
We consider the following reactions for the upper cycle in Fig. 9:

$$ \begin{aligned} &Y_1 + A \mathrel{\mathop{{\rightleftharpoons}}\limits^{{a}}_{{d}}} C_{A} \mathrel{\mathop{{\longrightarrow}}\limits^{{k}}} Y^*_1 + A \\ &Y^*_1 + D\mathrel{\mathop{{\rightleftharpoons}} \limits^{{a^{\prime}}}_{{d^{\prime}}}} \,C_{D} \mathrel{\mathop{{\longrightarrow}}\limits^{{k^{\prime}}}} Y_1 + D \end{aligned} $$

(32)

with A and D the activator and inactivator enzymes, respectively. Assuming A and D are approximately constants and solving for the steady-states, we obtain:

$$ y_1=\omega y_1^* $$

(33)

with $\omega=(k^{\prime} K_m D)/(k K_m^{\prime} A)$. This last result implies that the conservation law for the protein in the upper cycle con be written (neglecting the complexes with the activator and the inactivator, but not those with the downstream targets, and dividing the equation by Y _1T ) as: 1 = $y_{1}^{*}$(1 + ω) + c ₁ + c ₂, with c ₁ and c ₂ the normalized complexes with the downstream (double-phosphorylation) cycle. By writing the corresponding equations for c ₁ and c ₂, solving for the steady-state, and using the previous conservation, we obtain Eq. (18).