Derivation and analysis of parallel-in-time neural ordinary differential equations

Abstract

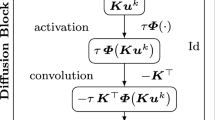
The introduction in 2015 of Residual Neural Networks (RNN) and ResNET allowed for outstanding improvements of the performance of learning algorithms for evolution problems containing a “large” number of layers. Continuous-depth RNN-like models called Neural Ordinary Differential Equations (NODE) were then introduced in 2019. The latter have a constant memory cost, and avoid the a priori specification of the number of hidden layers. In this paper, we derive and analyze a parallel (-in-parameter and time) version of the NODE, which potentially allows for a more efficient implementation than a standard/naive parallelization of NODEs with respect to the parameters only. We expect this approach to be relevant whenever we have access to a very large number of processors, or when we are dealing with high dimensional ODE systems. Moreover, when using implicit ODE solvers, solutions to linear systems with up to cubic complexity are then required for solving nonlinear systems using for instance Newton’s algorithm; as the proposed approach allows to reduce the overall number of time-steps thanks to an iterative increase of the accuracy order of the ODE system solvers, it then reduces the number of linear systems to solve, hence benefiting from a scaling effect.