Sell to whom? Firm’s green production in competition facing market segmentation

Abstract

When substantial numbers of consumers claim to be “green”, firms face the choice of whether to develop green products which are more environmental than their traditional counterparts. In many cases, consumers may differ in their willingness-to-pay for the green products that firms should determine which segment to sell the green products to. This paper examines the role of costs, consumer’s green segmentation, and competition in firm’s green production decisions. We find that the cost conditions for green production is relaxed in competition cases compared with the monopolist case. Under competition, the traditional firm would possibly to defend his market share via decreasing the traditional product’s price, which leading to an equilibrium that green products are sold to green segment solely. And we show that in some cases, both traditional and green firms can benefit from a large green segment ratio and consumer’s premium differentiation.Big data contains huge value through which we can better understand consumers. Based on big data technologies development, consumers can be accurate segmented with improved indexes of green premium and segment ratio, thus these conclusions can provide guidance to green production in practice.

Appendices

Appendixes

1.1 Proof of Proposition 1 and Corollary 1

Proof

We solve the problem in different pricing regimes and give the global optimal decisions buy maximizing the manufacturer’s profit in different pricing regimes. $\square$

1.2 Case 1: ${{p_g}}\ge {{k_l}}+{{p_t}}$ and ${{p_g}}\ge (1+k_h)p_t$

In this price regime, primary segment’s demand is given in Eq. 1 and green segment’s demand is given in Eq. 2. Then the manufacturer’s problem is:

$$\begin{aligned} \varPi \left( {{p_t},{p_g}} \right) = A{p_t}\left( {1 - {p_t} - \beta + \beta \frac{{{p_g} - {p_t}}}{{{k_h}}}} \right) \mathrm{{}} + A \left( {{p_g} - {c_g}} \right) \beta \left( {1 - \frac{{{p_g} - {p_t}}}{{{k_h}}}} \right) \end{aligned}$$

(13)

The first and second derivation of $\varPi$ regarding ${p_t}$ and ${p_g}$ respectively are:

$$\begin{aligned}&\displaystyle \frac{{\partial \varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}}} = A\frac{{\left( {1 - 2{p_t}} \right) {k_h} - \beta ({c_g} + {k_h} - 2{p_g} + 2{p_t}}}{{{k_h}}}= 0;\\&\displaystyle \frac{{\partial \varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_g}}} = A\frac{{\beta \left( {{c_g} + {k_h} - 2{p_g} + 2{p_t}} \right) }}{{{k_h}}}=0;\\&\displaystyle \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_t}}} = A\frac{{ - 2\beta - 2{k_h}}}{{{k_h}}}<0;\\&\displaystyle \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_g}}} = - A\frac{{2\beta }}{{{k_h}}}<0;\\&\displaystyle \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}\partial {p_g}}}=A\frac{{2\beta }}{{{k_h}}}. \end{aligned}$$

The determinant of Hessian can be written as: $\left| H \right| \mathrm{{ = }}A^2\frac{{\beta (1\mathrm{{ + }}2\beta {k_h})}}{{{k_h}^2}}>0$. Thus, the solution to the first order conditions gives the unique maximizer. The monopolist’s optimal prices under Case 1 can be obtained as:

$$\begin{aligned} p_t^*=\frac{1}{2} ,p_g^*=\frac{1+c_g+k_h}{2} \end{aligned}$$

where the sales quantities can be obtained as:

$$\begin{aligned} q_t^ * = A\frac{{{k_h} + \beta \left( {{c_g} - {k_h}} \right) }}{{2{k_h}}}, \quad q_g^ * = A\frac{{\beta \left( { - {c_g} + {k_h}} \right) }}{{2{k_h}}} \end{aligned}$$

The constraint ${{p_g}}\ge {{k_l}}+{{p_t}}$ is satisfied when $c_g\ge 2k_l-k_h$. The constraint ${{p_g}}\ge (1+k_h)p_t$ is satisfied of $c_g>0$. To guarantee positive demand, $c_g<k_h$ is required. Otherwise, no green products are sold. There is only traditional products offered to the market and $p_t^*=\frac{1}{2}$.

1.3 Case 2: ${{p_g}}\ge {{k_l}}+{{p_t}}$ and ${{p_g}}< (1+k_h)p_t$

In this price regime, primary segment’s demand is given in Eq. 1 and green segment’s demand is given in Eq. 3. Then the manufacturer’s problem is:

$$\begin{aligned} \varPi \left( {{p_t},{p_g}} \right) = A{p_t}\left( {1 - \beta } \right) \left( {1 - {p_t}} \right) \mathrm{{}} + A\left( {{p_g} - {c_g}} \right) \beta \left( 1 - \frac{{{p_g}}}{{1 + {k_h}}}\right) \end{aligned}$$

(14)

The monopolist’s optimal prices under Case 2 is the same as the solutions in Case 1 that:

$$\begin{aligned} p_t^*=\frac{1}{2}, \quad p_g^*=\frac{1+c_g+k_h}{2} \end{aligned}$$

The constraint ${{p_g}}< (1+k_h)p_t$ is satisfied only when $c_g<0$. The optimal price is on the boundary and thus is suboptimal to Case 1.

1.4 Case 3: $(1+k_h)p_t\le p_g<k_l+p_t$

In this price regime, primary segment’s demand is given in Eq. 4 and green segment’s demand is given in Eq. 2. We define $\varDelta \buildrel \textstyle .\over = {k_h} - {k_l}$ for simplicity. Then the manufacturer’s problem is:

$$\begin{aligned} \varPi \left( {{p_t},{p_g}} \right)= & {} {p_t}A\left( {\left( {1 - \beta } \right) \left( {\frac{{{p_g} - {p_t}}}{{{k_l}}} - {p_t}} \right) + \beta \left( {\frac{{{p_g} - {p_t}}}{{{k_h}}} - {p_t}} \right) } \right) \mathrm{{}} \end{aligned}$$

(15)

$$\begin{aligned}= & {} \left( {{p_g} - {c_g}} \right) A\left( {\left( {1 - \beta } \right) \left( {1 - \frac{{{p_g} - {p_t}}}{{{k_l}}}} \right) + \beta \left( {1 - \frac{{{p_g} - {p_t}}}{{{k_h}}}} \right) } \right) \\ \frac{{\partial \varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}}}= & {} A\frac{{{c_g}\left( {\left( { - 1 + \beta } \right) \varDelta - {k_l}} \right) - 2\left( {{k_l}\left( { - {p_g} + {p_t} + {p_t}{k_l}} \right) } \right) }}{{{k_l}{k_h}}};\nonumber \\&+ \,A\frac{{{c_g}\varDelta \left( {\left( { - 1 + \beta } \right) {p_g} + {p_t}\left( {1 - \beta + {k_l}} \right) } \right) }}{{{k_l}{k_h}}};\nonumber \\ \frac{{\partial \varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_g}}}= & {} A\frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}\left( { - 2{p_g} + 2{p_t} + {k_l}} \right) }}{{{k_l}{k_h}}} ;\nonumber \\&+ \,A\frac{{\varDelta \left( {2\left( { - 1 + \beta } \right) {p_g} + 2{p_t} - 2\beta {p_t} + {k_l}} \right) }}{{{k_l}{k_h}}} ;\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_t}}}= & {} - A \frac{{2\left( {{k_l}\left( {1 + {k_l}} \right) + \varDelta \left( {1 - \beta + {k_l}} \right) } \right) }}{{{k_l}{k_h}}}<0 ;\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_g}}}= & {} A\frac{{2\left( { - 1 + \beta } \right) \varDelta - 2{k_l}}}{{{k_l}{k_h}}} < 0 ;\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}\partial {p_g}}}= & {} - A\frac{{2\left( {\left( { - 1 + \beta } \right) \varDelta - {k_l}} \right) }}{{{k_l}{k_h}}}.\nonumber \end{aligned}$$

(16)

The determinant of Hessian can be written as: $\left| H \right| = {A^2}\frac{{4\left( {{k_h} - \beta \varDelta } \right) }}{{{k_l}{k_h}}}>0$. Thus, the monopolist’s optimal prices under the low-price regime can be obtained as:

$$\begin{aligned}&\displaystyle p_t^*=\frac{1}{2}, p_g^*=\frac{1+c_g}{2} +\frac{k_l k_h}{2(k_h-\beta \varDelta )}\\&\displaystyle q_t^*=A\frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) }}{{2{k_l}{k_h}}}, p_g^*=A\frac{{{c_g}\left( {\left( { - 1 + \beta } \right) \varDelta - {k_l}} \right) + {k_l}{k_h}}}{{2{k_l}{k_h}}} \end{aligned}$$

The constraint $p_g\ge (1+k_h)p_t$ is satisfied when ${c_g}>\frac{{{k_h} \varDelta \left( {1 - \beta } \right) }}{{k_h} - \beta \varDelta }$. The constraint $p_g< k_l+ p_t$ is satisfied when $\varDelta <k_l$ and ${c_g} < \frac{{{k_l}\left( {{k_h} - 2\beta \varDelta } \right) }}{{{k_h} - \beta \varDelta }}$. Then, the solutions in this case is feasible when $\varDelta <k_l$ and $\frac{{{k_h} \varDelta \left( {1 - \beta } \right) }}{{k_h} - \beta \varDelta }< {c_g} < \frac{{{k_l}\left( {{k_h} - 2\beta \varDelta } \right) }}{{{k_h} - \beta \varDelta }}$. If the constraints are not satisfied, this solutions are suboptimal to the solutions in other cases.

1.5 Case 4: ${{p_g}}<{{k_l}}+{{p_t}}$ and $p_g<(1+k_h)p_t$

In this price regime, primary segment’s demand is given in Eq. 4 and green segment’s demand is given in Eq. 3. Then the manufacturer’s problem is:

$$\begin{aligned} \varPi \left( {{p_t},{p_g}} \right)= & {} A(1 - \beta )\left( \frac{{{p_g} - {p_t}}}{{{k_l}}} - {p_t}\right) {p_t} \\&+\,A\left( {1 - \left( {1 - \beta } \right) \frac{{{p_g} - {p_t}}}{{{k_l}}}- \beta \frac{{{p_g}}}{{1 + {k_h}}}} \right) \left( {{p_g} - {c_g}} \right) \nonumber \\ \frac{{\partial \varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}}}= & {} A\frac{{\left( { - 1 + \beta } \right) \left( {{c_g} + 2\left( { - {p_g} + {p_t} + {p_t}{k_l}} \right) } \right) }}{{{k_l}}};\nonumber \\ \frac{{\partial \pi \left( {{p_t},{p_g}} \right) }}{{\partial {p_g}}}= & {} A\frac{{({c_g} + 2{p_g})\left( {\beta + \beta \varDelta } \right) }}{{{k_l}\left( {1 + {k_h}} \right) }} + A\frac{{2\left( {1 - \beta } \right) {p_t} + {k_l} + {c_g} - 2{p_g}}}{{{k_l}}};\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_t}}}= & {} A\frac{{2\left( { - 1 + \beta } \right) \left( {1 + {k_l}} \right) }}{{{k_l}}}< 0;\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{{\partial ^2}{p_g}}}= & {} A\frac{{2\left( { - 1 + \beta - {k_h} + \beta \varDelta } \right) }}{{{k_l}\left( {1 + {k_h}} \right) }} < 0;\nonumber \\ \frac{{{\partial ^2}\varPi \left( {{p_t},{p_g}} \right) }}{{\partial {p_t}\partial {p_g}}}= & {} - A\frac{{2\left( { - 1 + \beta } \right) }}{{{k_l}}}.\nonumber \end{aligned}$$

(17)

The determinant of Hessian can be written as: $\left| H \right| ={A^2}\frac{{4\left( { - 1 + \beta } \right) \left( { - 1 + \left( { - 1 + \beta } \right) \varDelta - {k_l}} \right) }}{{{k_l}\left( {1 + {k_h}} \right) }} > 0$. Thus, the monopolist’s optimal prices in this case can be obtained as:

$$\begin{aligned} p_t^*=\frac{1+k_h}{2(1+k_h-\beta \varDelta )}, p_g^*=\frac{c_g}{2}+\frac{(1+k_l)(1+k_h)}{2(1+k_h-\beta \varDelta )} \end{aligned}$$

The solutions in this case are feasible when $\varDelta >k_l$ and $0<{c_g} < \frac{{{k_l}\left( {1 + {k_h} - 2\beta \varDelta } \right) }}{{1 + {k_h} - \beta \varDelta }}$, where the constraints ${{p_g}}<{{k_l}}+{{p_t}}$ and $p_g<(1+k_h)p_t$ are satisfied. Otherwise, this case gives the boundary solutions which are suboptimal to other cases.

1.6 Case 5: $p_g<(1+k_l)p_t$

In this case, only green products are offered to the market, then the optimal solution is

$$\begin{aligned} p_g^*=\frac{c_g}{2}+\frac{(1+k_l)(1+k_h)}{2(1+k_h-\beta \varDelta )}, \end{aligned}$$

it is always suboptimal to the

1.7 Comparing the profits in different cases to give optimal solutions

Given the optimal prices in different pricing regimes, we first assume all the cost constraint is satisfied that the prices regimes are feasible. The manufacturer’s decision can be found as follows: If $\varDelta <k_l$, Case 1 and Case 3 are feasible. The firm’s profit in case 1 is higher than the profit in case 3 when

$$\begin{aligned} \beta > {\tilde{\beta }_1} = \frac{{{{({c_g} - {k_l})}^2}{k_h}}}{{\varDelta (c_g^2 - 2{c_g}{k_l} + {k_l}{k_h})}}. \end{aligned}$$

When $\beta \le {\tilde{\beta }_1}$, the profit in Case 3 is higher than the profit in Case 1. Thus, firm’s optimal solution changes in how large the green segment is.

If $\varDelta >k_l$, Case 1 and Case 4 are feasible, the firm determines the optimal prices by comparing the profits in two cases. When $\beta > {\tilde{\beta }_2}$, the manufacturer’s profit in Case 1 is higher than the profit in Case 4. Otherwise, the profit in Case 4 is higher than the profit in Case 1. Here ${\tilde{\beta }_2}$ is obtained by solving ${\varPi ^ * }(case1) = {\varPi ^ * }(case4)$, the expression of ${\tilde{\beta }_2}$ is given as:

$$\begin{aligned} {{\tilde{\beta }}_2}&= \frac{{\left( {1 + {k_h}} \right) (n - \sqrt{n - 2{k_h}{{\left( {{c_g} - {k_l}} \right) }^2}m} )}}{m}\\ m&\buildrel \textstyle .\over = 2\varDelta \left( { - 2{c_g}{k_h}\left( {1 + {k_h}} \right) {k_l} + k_h^2\left( {1 + {k_h}} \right) {k_l} + c_g^2\left( {{k_l} + {k_h}\left( {1 + {k_h}} \right) } \right) } \right) \\ n&\buildrel \textstyle .\over = - 2{c_g}{k_h}\left( {1 + \varDelta + {k_h}} \right) {k_l} + {k_h}{k_l}\left( {{k_l} + k_h^2} \right) + c_g^2\left( {{k_l} + {k_h}\left( {1 + \varDelta + {k_h}} \right) } \right) \end{aligned}$$

The optimal solutions implies that the firm should change the pricing regions in the consumers’ premium and the green segment size. With large green segment in the market, i.e., $\beta > {\tilde{\beta }_1}({\tilde{\beta }_2})$ the price equilibrium exists in the region ${{p_g}} \ge {{k_l}}+{{p_t}}$ (see Case 1) where green products are only sold to green segment. With a small green segment i.e., $\beta < {\tilde{\beta }_1}({\tilde{\beta }_2})$, the price equilibrium exists in the region ${{p_g}} \ge {{k_l}}+{{p_t}}$ (see Cases 3 and 4) where green products are sold to both segment. In this price switching strategy, the firm can get maximized profits from the whole market.

Proof of Corollary 2

Proof

In high price regime, cost conditions are such that the prices in Proposition 1 is feasible, the first order condition is:

$$\begin{aligned} \frac{{d\varPi }}{{d\beta }}=\frac{{{{\left( { - {c_g} + {k_h}} \right) }^2}}}{{4{k_h}}} >0 \end{aligned}$$

In the low price regime in case 1, the first order condition is:

$$\begin{aligned} \frac{{d\varPi }}{{d\beta }}=\frac{{\varDelta \left( {{k_l}^2{k_h}^2 - {c_g}^2{{\left( {{k_h} - \beta \varDelta } \right) }^2}} \right) }}{{4{k_l}{k_h}{{\left( {{k_h} - \beta \varDelta } \right) }^2}}}>0 \end{aligned}$$

In the low price regime in case 2, the first order condition is:

$$\begin{aligned} \frac{{d\varPi }}{{d\beta }}=\frac{{\varDelta {k_l}\left( {1 + {k_l}} \right) {{\left( {1 + {k_h}} \right) }^2} - {c_g}^2\left( {1 + \varDelta } \right) {{\left( {1 + {k_h} - \beta \varDelta } \right) }^2}}}{{4{k_l}\left( {1 + {k_h}} \right) {{\left( {1 + {k_h} - \beta \varDelta } \right) }^2}}}>0 \end{aligned}$$

$\square$

Proof of Proposition 2

1.1 Firm 1’s best response function

Proof

Firm 1’s best response function is obtained as follows.

Case 1. When ${p_1} \le {p_2} - {k_l}$ and ${p_1} \le \frac{{{p_2}}}{{(1 + {k_h})}}$, Firm 1 price the traditional product low and his problem is given by:

$$\begin{aligned} \mathop {\max }\limits _{{p_1}} {\varPi _1}\left( {{p_1}\left| {{p_2}} \right. } \right)= & {} A{p_1} \left( {1 - \beta - {p_1} + \beta \frac{{{p_2} - {p_1}}}{{{k_h}}}} \right) \end{aligned}$$

(18)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\mathrm{{. }}~~{p_1}\le & {} \frac{{{p_2}}}{{1 + {k_h}}} \end{aligned}$$

(19)

$$\begin{aligned} {p_1}\le & {} {p_2} - {k_l} \end{aligned}$$

(20)

The optimal solution for the unconstraint problem is ${p_{1}}=\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }}$ and the optimal profit is:

$$\begin{aligned} \varPi _1^{case1}=\frac{{{{\left( {\left( {1\mathrm{{ - }}\beta } \right) {k_h}\mathrm{{ + }}\beta {p_2}} \right) }^2}}}{{4{k_h}\left( {\beta + {k_h}} \right) }} \end{aligned}$$

Constraint (19) is met when ${p_2} \ge \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}}$. Constraint (20) is met when ${p_2} > \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$.

When $\frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}}>\frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$, (the condition for this inequity is ${k_l}< \varDelta$ and $\beta < \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$.) if ${p_2} < \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}}$, constraint (19) is violated and ${p_1} = \frac{{{p_2}}}{{1 + {k_h}}}$. Constraint (20) is met when ${p_2}\ge \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}}$. Then, Firm 1’s optimal price is given by:

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} \,\, {p_2} \ge \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} ,\\ {\frac{{{p_2}}}{{1 + {k_h}}},}&{} \quad \mathrm{if} \,\, \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} \le {p_2} < \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} ,\\ {\textit{Infeasible},} &{} \quad \mathrm{otherwise} .\ \end{array}} \right. \end{aligned}$$

(21)

When $\frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} \le \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$ (the condition for this inequity is ${k_l}< \varDelta$ and $\beta \ge \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$; or ${k_l} \ge \varDelta$), $\frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}}> \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$ always holds. Firm 1’s optimal price is given by:

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} \,\, {p_2} \ge \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}} ,\\ {{p_2} - {k_l},}&{} \quad \mathrm{if} \,\, {p_2}< \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}} .\ \end{array}} \right. \end{aligned}$$

(22)

Case 2. When ${p_1} \le {p_2} - {k_l}$, and ${p_1} >\frac{{{p_2}}}{{1 + {k_h}}}$, Firm 1’ problem is given by:

$$\begin{aligned} \mathop {\max }\limits _{{p_1}} {\varPi _1}\left( {{p_1}\left| {{p_2}} \right. } \right)= & {} A{p_1}\left( {1 - \beta } \right) \left( {1 - {p_1}} \right) \mathrm{{}} \end{aligned}$$

(23)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\mathrm{{. }}{p_1}> & {} \frac{{{p_2}}}{{1 + {k_h}}} \end{aligned}$$

(24)

$$\begin{aligned} {p_1}\le & {} {p_2} - {k_l} \end{aligned}$$

(25)

The optimal price of the unconstraint problem is: ${p_1}=\frac{1}{2}$ and $\varPi _1^{case2} = \frac{{1 - \beta }}{4}$. The constraint is satisfied when $\frac{1}{2} + {k_l} < {p_2} \le \frac{{1 + {k_h}}}{2}$. If ${k_l}>\varDelta$, $\frac{1}{2} + {k_l} \ge \frac{{1 + {k_h}}}{2}$, no infeasible region for the price regime. in Case 2, we only consider the case ${p_2} <\frac{{1 + {k_h}}}{2}$. Otherwise, constraint ${p_1} >\frac{{{p_2}}}{{1 + {k_h}}}$ is violated and Case 1 is superior. When ${k_l}< \varDelta$, Firm 1’s optimal price is given by

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{1}{2},}&{} \quad \mathrm{if} \,\, \frac{1}{2} + {k_l}< {p_2} \le \frac{{1 + {k_h}}}{2} ,\\ { {p_2} - {k_l},}&{} \quad \mathrm{if} \,\, \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} < {p_2}\le \frac{1}{2} + {k_l},\\ {\textit{Infeasible}, }&{} \quad \mathrm{otherwise}.\ \end{array}} \right. \end{aligned}$$

(26)

Combining Case 1 and Case 2. If ${k_l}>\varDelta$, case 2 is infeasible and $\frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} > \frac{{{k_h} - \beta {k_h} + 2{k_h}{k_l}}}{{\beta + 2{k_h}}}$ is violated. The only feasible solution is Eq. 22 in Case 1.

If ${k_l}<\varDelta$, $\varPi _1^{case2} >\varPi _1^{case1}$ when

$$\begin{aligned} \frac{{ - \left( {1 - \beta } \right) {k_h} - \sqrt{\left( {1 - \beta } \right) {k_h}\left( {\beta + {k_h}} \right) } }}{\beta }< {p_2} < \frac{{ - \left( {1 - \beta } \right) {k_h} + \sqrt{\left( {1 - \beta } \right) {k_h}\left( {\beta + {k_h}} \right) } }}{\beta } \end{aligned}$$

Here we define ${p_2^I}=\frac{{ - \left( {1 - \beta } \right) {k_h} + \sqrt{\left( {1 - \beta } \right) {k_h}\left( {\beta + {k_h}} \right) } }}{\beta }$. Note that $\max \{ \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}},\frac{{{k_h} - \beta {k_h} + 2{k_h}{k_l}}}{{\beta + 2{k_h}}}\}<{p_2^I}< \frac{{1 + {k_h}}}{2}$ . Then, combining the two cases. When $0< \beta < \frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}$, ${p_{1}}=\frac{1}{2}$ is feasible, the response is given as:

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} ~ {p_2} \ge {p_2^I} ,\\ { \frac{1}{2},}&{} \quad \mathrm{if} ~ \frac{1}{2} + {k_l} \le {p_2}< {p_2^I},\\ { {p_2} - {k_l},}&{} \quad \mathrm{if} ~ \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} < {p_2}\le \frac{1}{2} + {k_l},\\ { \textit{Infeasible}, }&{} \quad \mathrm{otherwise}.\ \end{array}} \right. \end{aligned}$$

(27)

When $\beta > \frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}$, ${p_{1}}=\frac{1}{2}$ is not feasible, the response is given in Case 1.

Case 3. When ${p_1} > {p_2} - {k_l}$ and ${p_1} \le \frac{{{p_2}}}{{1 + {k_h}}}$, Firm 1 price the traditional product high and his problem is given by:

$$\begin{aligned} \mathop {\max }\limits _{{p_1}} {\varPi _1}\left( {{p_1}\left| {{p_2}} \right. } \right)= & {} A\left( { - {p_1} + \beta \frac{{{p_2} - {p_1}}}{{{k_h}}} + \left( {1 - \beta } \right) \frac{{{p_2} - {p_1}}}{{{k_l}}}} \right) {p_1}\end{aligned}$$

(28)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\mathrm{{. }}~~{p_1}> & {} {p_2} - {k_l}\end{aligned}$$

(29)

$$\begin{aligned} {p_1}\le & {} \frac{{{p_2}}}{{1 + {k_h}}} \end{aligned}$$

(30)

The optimal solution of the unconstraint problem is ${p_{1}}=\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }}$ and

$$\begin{aligned} \varPi _1^{case3} = \frac{{{p_2}^2{{\left( {{k_h} - \beta \varDelta } \right) }^2}}}{{4{k_l}{k_h}\left( {{k_h} - \beta \varDelta + {k_h}{k_l}} \right) }} \end{aligned}$$

Constraint ${p_1} > {p_2} - {k_l}$ is satisfied when ${p_2} < \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}$. Constraint ${p_1} \le \frac{{{p_2}}}{{1 + {k_h}}}$ is always satisfied when ${p_2}\ge 0$. Then Firm 1’s optimal price is given by:

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }},}&{}\quad \mathrm{if}~ {p_2}< \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}} ,\\ { {p_2} - {k_l}, }&{} \quad \mathrm{if} \,\, \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}\le {p_2}< \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} ,\\ {\textit{Infeasible},}&{} \quad \mathrm{if} \,\, {p_2}\ge \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} .\ \end{array}} \right. \end{aligned}$$

(31)

Case 4. When ${p_1} > {p_2} - {k_l}$ and ${p_1} > \frac{{{p_2}}}{{(1 + {k_h})}}$, Firm 1’s problem is given by $A(1 - \beta )\mathrm{{(}}\frac{{{p_2} - {p_1}}}{{{k_l}}} - {p_1}\mathrm{{)}}{p_1}$. Solution of the unconstraint problem is ${p_1} = \frac{{{p_2}}}{{2\left( {1 + {k_l}} \right) }}$, Constraint ${p_1} > \frac{{{p_2}}}{{1 + {k_h}}}$ is violated when ${p_2}>0$. Then for any ${p_2}>0$, the objective function in Case 3 is superior and is achievable by choosing (31).

Combining 4 Cases to obtain the best-response of Firm 1. When ${k_l}< \varDelta$, and $0< \beta < \frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}$, Firm 1’s best response function is given as:

$$\begin{aligned} {p_{1}}=\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} \,\, {p_2} \ge {p_2^I} ,\\ { \frac{1}{2},}&{} \quad \mathrm{if} \,\, \frac{1}{2} + {k_l} \le {p_2}< {p_2^I},\\ { {p_2} - {k_l}, }&{} \quad \mathrm{if} \,\, \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}\le {p_2}<\frac{1}{2} + {k_l} ,\\ {\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }},}&{} \quad \mathrm{if} \,\, {p_2} < \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}.\ \end{array}} \right. \end{aligned}$$

(32)

$\frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}\le \beta < \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, Firm 1’s best response function is given as:

$$\begin{aligned} {p_{1}} =\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} {p_2} \ge \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} ,\\ {\frac{{{p_2}}}{{1 + {k_h}}},}&{} \quad \mathrm{if} \,\, \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} \le {p_2}< \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}} ,\\ { {p_2} - {k_l}, }&{} \quad \mathrm{if} \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}\le {p_2}< \frac{{{k_l}\left( {1 + {k_h}} \right) }}{{{k_h}}} ,\\ {\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }},}&{} \quad \mathrm{if} \,\,{p_2} < \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}.\ \end{array}} \right. \end{aligned}$$

(33)

When $\beta \ge \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, Firm 1’s best response function is the same as the case when ${k_l}\ge \varDelta$. When ${k_l}\ge \varDelta$, Firm 1’s best response function is given as:

$$\begin{aligned} {p_{1}} =\left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }},}&{} \quad \mathrm{if} \,\,{p_2} \ge \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}} ,\\ {{p_2} - {k_l},}&{}\quad \mathrm{if}~ \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}\le {p_2}< \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}} ,\\ {\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }},}&{} \quad \mathrm{if} \,\,{p_2} < \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}.\ \end{array}} \right. \end{aligned}$$

(34)

$\square$

1.2 Firm 2’s best response function

Proof

Case 1. Given a $p_1$, if Firm 2 wants to sell to the green segment only he can price his products high, i.e., $p_2\ge k_l+p_1$, if $p_2\ge (1+ k_h)p_1$, some green consumers purchase the traditional products, Firm 2’s problem is:

$$\begin{aligned} \mathop {\max }\limits _{p_2 } \varPi _2 \left( {p_2 \left| {p_1 } \right. } \right)= & {} A \beta (1-\frac{p_2-p_1}{k_h})(p_2-c_g) \end{aligned}$$

(35)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\mathrm{{. }}~~{p_2}\ge & {} {p_1} + {k_l}\end{aligned}$$

(36)

$$\begin{aligned} {p_2}\ge & {} ({1 + {k_h}}){p_1} \end{aligned}$$

(37)

The optimal solution of the unconstraint problem is ${p_{2}} = \frac{1}{2}\left( {{c_g} + {k_h} + {p_1}} \right)$ and the maximized profit is given as:

$$\begin{aligned} \varPi _2^{case1} = \frac{{\beta {{\left( { - {c_g} + {k_h} + {p_1}} \right) }^2}}}{{4{k_h}}} \end{aligned}$$

Constraint $p_2\ge k_l+p_1$ is satisfied when $p_1\le c_g+k_h-2k_l$. Constraint $p_2\ge (1+ k_h)p_1$ is satisfied when ${p_1} \le \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}$.

Therefore, when $c_g+k_h-2k_l\le \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}$, (or equivalently, ${c_g} \le \frac{{ - {\varDelta ^2} + {k_l} + {k_l}^2}}{{{k_h}}}$), if $p_1> c_g+k_h-2k_l$, the candidate solution is $p_{2}=k_l+p_1$ , constraint ${p_2} \ge ({1 + {k_h}}){p_1}$ is met when $p_1 \le \frac{{{k_l}}}{{{k_h}}}$. Then, the optimal price for Firm 2 in this price region is given by:

$$\begin{aligned} {p_{2}} =\left\{ {\begin{array}{*{20}{ll}} {\textit{Infeasible},}&{} \quad \mathrm{if} \,\,p_1> \frac{{{k_l}}}{{{k_h}}} ,\\ {k_l+p_1,}&{} \quad \mathrm{if} \,\, c_g+k_h-2k_l< p_1 \le \frac{{{k_l}}}{{{k_h}}} ,\\ {\frac{1}{2}\left( {{c_g} + {k_h} + {p_1}} \right) , }&{} \quad \mathrm{if} p_1\le c_g+k_h-2k_l.\ \end{array}} \right. \end{aligned}$$

(38)

When $c_g+k_h-2k_l>\frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}$ (or equivalently, ${c_g}>\frac{{ - {\varDelta ^2} + {k_l} + {k_l}^2}}{{{k_h}}}$). $\frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}>\frac{{{k_l}}}{{{k_h}}}$ always holds. The optimal price for Firm 2 is given by

$$\begin{aligned} {p_{2}} =\left\{ {\begin{array}{*{20}{ll}} {(1+ k_h)p_1,}&{} p_1 > \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}} ,\\ {\frac{1}{2}\left( {{c_g} + {k_h} + {p_1}} \right) ,}&{} \quad \mathrm{if} \,\,p_1 \le \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}} .\ \end{array}} \right. \end{aligned}$$

(39)

Case 2. When $p_2\ge k_l+p_1$ and $p_2<(1+ k_h)p_1$, where Firm 2’ s problem is $A\left( {{p_2} - {c_g}} \right) \beta (1 - \frac{{{p_2}}}{{1 + {k_h}}})$, the optimal solution of the unconstraint problem is $p_2=\frac{1+c_g+k_h}{2}$ and

$$\begin{aligned} \varPi _2^{case2} = \frac{{\beta \left( {2 - {c_g} + {k_h} - {p_1}} \right) \left( { - {c_g} + {k_h} + {p_1}} \right) }}{{4\left( {1 + {k_h}} \right) }} \end{aligned}$$

The feasible region for the interior optimal solution is $\frac{{1 + {c_g} + {k_h}}}{{2 + 2{k_h}}} \le {p_1} < \frac{1}{2}\left( 1 + {c_g} + {k_h} - 2{k_l} \right)$. Comparing the objects in Case 1 and Case 2, $\varPi _2^{case2} > \varPi _2^{case1}$ when ${c_g} - {k_h}< {p_1} < \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}$. This price region is not within the boundary of the feasible region of Case 2, i.e., ${p_1}\ge \frac{{1 + {c_g} + {k_h}}}{{2 + 2{k_h}}}$ (because the inequality $\frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}} < \frac{{1 + {c_g} + {k_h}}}{{2 + 2{k_h}}}$ always holds). Therefore, the solution in Case 2 is always suboptimal to the solution in Case 1.

Case 3. $p_2<k_l+p_1$ and $p_2\ge (1+ k_h)p_1$ . Firm 2’ s problem is:

$$\begin{aligned} \mathop {\max }\limits _{p_2 } \varPi _2 \left( {p_2 \left| {p_1 } \right. } \right)= & {} A \left( 1-\beta \frac{p_2-p_1}{k_h} -(1- \beta ) \frac{p_2-p_1}{k_l}\right) (p_2-c_g) \end{aligned}$$

(40)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\,\,\mathrm{{. }}~~{p_2}< & {} {p_1} + {k_l}\end{aligned}$$

(41)

$$\begin{aligned} {p_2}\ge & {} ({1 + {k_h}}){p_1} \end{aligned}$$

(42)

The optimal solution of the unconstraint problem is ${p_{2}} = \frac{{{c_g} + {p_1}}}{2} + \frac{{{k_l}{k_h}}}{{2({k_h} - \beta \varDelta )}}$ and the profit is

$$\begin{aligned} \varPi _2^{case3} =\frac{{{{\left( {{c_g}\left( {\left( { - 1 + \beta } \right) {k_h} - \beta {k_l}} \right) + \beta {k_l}{p_1} + {k_h}\left( {{k_l} + {p_1} - \beta {p_1}} \right) } \right) }^2}}}{{4{k_h}{k_l}\left( {{k_h} - \beta \varDelta } \right) }} \end{aligned}$$

Constraint $p_2<k_l+p_1$ is satisfied when ${p_1} > {c_g} - \frac{{{k_l}({k_h} - 2\beta \varDelta )}}{{{k_h} - \beta \varDelta }}$. Constraint $p_2\ge (1+ k_h)p_1$ is satisfied when ${p_1} \le \frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}$. Then Firm 2’s optimal price is given by

$$\begin{aligned} {p_{2}} =\left\{ {\begin{array}{*{20}{ll}} {\textit{Infeasible},}&{} \quad \mathrm{if} \,\,p_1> \frac{{{k_l}}}{{{k_h}}} ,\\ {(1+ k_h)p_1,}&{} \quad \mathrm{if} \,\,\frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}< {p_1} \le \frac{{{k_l}}}{{{k_h}}} ,\\ {\frac{{{c_g} + {p_1}}}{2} + \frac{{{k_l}{k_h}}}{{2({k_h} - \beta \varDelta )}},}&{} \quad \mathrm{if} \,\,{c_g} - \frac{{{k_l}({k_h} - 2\beta \varDelta )}}{{({k_h} - \beta \varDelta )}}<{p_1} \le \frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }} ,\\ { k_l+p_1, }&{} \quad {p_1}\le {c_g} - \frac{{{k_l}({k_h} - 2\beta \varDelta )}}{{{k_h} - \beta \varDelta }}.\ \end{array}} \right. \end{aligned}$$

(43)

Case 4. $p_2<k_l+p_1$ and $p_2<(1+ k_h)p_1$. Firm 2’s problem is given as:

$$\begin{aligned} \mathop {\max }\limits _{p_2 } \varPi _2 \left( {p_2 \left| {p_1 } \right. } \right)= & {} A\left( {1 - \left( {1 - \beta } \right) \frac{{{p_2} - {p_1}}}{{{k_l}}} - \beta \frac{{{p_2}}}{{1 + {k_h}}}} \right) \left( {{p_2} - {c_g}} \right) \end{aligned}$$

(44)

$$\begin{aligned} \mathrm{{s}}\mathrm{{.t}}\mathrm{{. }}~~ {p_2}< & {} {p_1} + {k_l}\end{aligned}$$

(45)

$$\begin{aligned} {p_2}< & {} ({1 + {k_h}}){p_1} \end{aligned}$$

(46)

The optimal price of the unconstraint problem is: ${p_2}\mathrm{{ = }}\frac{{{c_g}}}{2} + \frac{{\left( {\left( {1 - \beta } \right) {p_1} + {k_l}} \right) \left( {1 + {k_h}} \right) }}{{2(1 - \beta + {k_h} - \beta \varDelta )}}$ and the profit is

$$\begin{aligned} \varPi _2^{case4} = - \frac{{{{\left( {{c_g}\left( { - 1 + \beta + \left( { - 1 + \beta } \right) {k_h} - \beta {k_l}} \right) + \left( {1 + {k_h}} \right) \left( {{k_l} - \left( { - 1 + \beta } \right) {p_1}} \right) } \right) }^2}}}{{4\left( {1 + {k_h}} \right) {k_l}\left( { - 1 + \beta + \left( { - 1 + \beta } \right) {k_h} - \beta {k_l}} \right) }} \end{aligned}$$

Constraint $p_2<k_l+p_1$ is satisfied when ${p_1} > \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_l}\left( {1 + {k_h} - 2\beta \left( {1 + \varDelta } \right) } \right) }}{{1 + {k_h} + \beta \left( { - 1 - \varDelta + {k_l}} \right) }}$. Constraint $p_2<(1+ k_h)p_1$ is satisfied when ${p_1} > \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_l}\left( {1 + {k_h}} \right) }}{{\left( {1 - \beta + 2{k_h} - 2\beta \varDelta } \right) \left( {1 + {k_h}} \right) }}$. We find only if the green cost is high enough that, Cases 3 and 4 are both feasible, i.e., ${c_g} > \frac{{{k_l} + {k_h}{k_l}}}{{{k_h} - \beta {k_h} + \beta {k_l}}}$. By solving the inequality $\varPi _2^{case3} < \varPi _2^{case4}$ we have the condition Firm 2 will choose his response in Case 4 when

$$\begin{aligned} {p_1}< \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_h}{k_l}}}{{1 - \beta + 2{k_h} - 2\beta {k_h} + \beta {k_l}}} + \frac{{\left( {1 + {k_h}} \right) {k_l} - {c_g}\left( {{k_h} - \beta \varDelta } \right) }}{{1 - \beta + 2{k_h} - 2\beta {k_h} + \beta {k_l}}}\sqrt{\frac{{{k_h}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) }}{{\left( {1 + {k_h}} \right) \left( {{k_h} - \beta \varDelta } \right) }}} \end{aligned}$$

There is no Nash equilibrium in Case 4 because Firm 1’s profits at this price region is always suboptimal, that Firm 1 would not price at this region. If ${c_g} > \frac{{{k_l} + {k_h}{k_l}}}{{{k_h} - \beta {k_h} + \beta {k_l}}}$, Case 4 is superior to Case 3 but no equilibrium exists. Then, we only need to discuss the situation when ${c_g} < \frac{{{k_l} + {k_h}{k_l}}}{{{k_h} - \beta {k_h} + \beta {k_l}}}$. In this cost condition, Case 4 is feasible when Firm 1’s price is high enough.

Combining Cases to obtain Firm 2’s best response function

$\varPi _2^{case1} >\varPi _2^{case3}$ when ${c_g} - {k_l} - \varDelta \sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}<{p_1}<{c_g} - {k_l} + \varDelta \sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}$.

Here we define ${p_1^I}={c_g} - {k_l} + \varDelta \sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}$. When $p_{1}<{c_g} - {k_l} - \varDelta \sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}$, the inequality ${c_g} - {k_l} - \varDelta \sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}} < {c_g} - \frac{{{k_l}({k_h} - 2\beta \varDelta )}}{{{k_h} - \beta \varDelta }}$ always holds, the candidate solution $p_{2}={k_l} + {p_1}$ in Case 3 is infeasible because constraint $p_{2}>{c_g}$ is violated. Then, Case 1 is the only feasible solution When $p_{1}\le {p_1^I}$. When ${p_1^I}<{p_1} \le \frac{{{c_g}\left( {{k_h}- \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}$, Case 3 is superior, where $\frac{{{c_g}\left( {{k_h}- \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}< \frac{{{c_g} + {k_h}}}{{1 + 2{k_h}}}$ and ${p_1^I}<{c_g} - 2{k_l}+ {k_h}$ always hold, Firm 2’s best response function is given as:

$$\begin{aligned} {p_{2}} =\left\{ {\begin{array}{*{20}{ll}} {\frac{1}{2}\left( {{c_g} + {k_h} + {p_1}} \right) , }&{} \quad \mathrm{if} {p_1} \le {p_1^I} ,\\ {\frac{{{c_g} + {p_1}}}{2} + \frac{{{k_l}{k_h}}}{{2({k_h} - \beta \varDelta )}},}&{} \quad \mathrm{if} \,\,{p_1^I}<{p_1} \le \frac{{{c_g}\left( {{k_h}- \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }} ,\\ {(1+ k_h)p_1,}&{} \quad \mathrm{if} \,\,\frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }} < {p_1} \le \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_l}\left( {1 + {k_h}} \right) }}{{\left( {1 - \beta + 2{k_h} - 2\beta \varDelta } \right) \left( {1 + {k_h}} \right) }} ,\\ {\frac{{{c_g}}}{2} + \frac{{\left( {\left( {1 - \beta } \right) {p_1} + {k_l}} \right) \left( {1 + {k_h}} \right) }}{{2(1 - \beta + {k_h} - \beta \varDelta )}},}&{} \quad \mathrm{otherwise} .\ \end{array}} \right. \end{aligned}$$

(47)

$\square$

1.3 Nash equilibrium if $\varDelta >{k_l}$

Proof

Case 1: When $p_2\ge k_l+p_1$, if $p_2\ge (1+ k_h)p_1$, ${p_{2}}=\frac{1}{2}\left( {{c_g} + {k_h} + {p_1}} \right)$ and ${p_{1}}=\frac{{{k_h} - \beta {k_h} + \beta \;{p_2}}}{{2\left( {\beta + {k_h}} \right) }}$ intersect at:

$$\begin{aligned} {p_1}= & {} - \frac{{ - \beta {c_g} - 2{k_h} + \beta {k_h}}}{{3\beta + 4{k_h}}}\\ {p_2}= & {} \frac{1}{2}\left( {{c_g} + {k_h}} \right) - \frac{{ - \beta {c_g} - 2{k_h} + \beta {k_h}}}{{2\left( {3\beta + 4{k_h}} \right) }} \end{aligned}$$

and the profits in equilibrium is:

$$\begin{aligned} {\varPi _1}= & {} \frac{{\left( {\beta + {k_h}} \right) {{\left( {\beta {c_g} - \left( { - 2 + \beta } \right) {k_h}} \right) }^2}}}{{{k_h}{{\left( {3\beta + 4{k_h}} \right) }^2}}}\\ {\varPi _2}= & {} \frac{{\beta {{\left( {{c_g}\left( {\beta + 2{k_h}} \right) - {k_h}\left( {1 + \beta + 2{k_h}} \right) } \right) }^2}}}{{{k_h}{{\left( {3\beta + 4{k_h}} \right) }^2}}} \end{aligned}$$

When $0< \beta < \frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}$, constraint for Firm 1 is to price at the region is ${p_2} > {p_2^I}$. Constraint for Firm 2 to price at the region is ${p_1} \le {{p_1}^I}$. The condition for the existence of the Nash equilibrium is ${c_g} >c_g^I$ which is obtained by solving the inequalities above. where $c_g^I=\max \{ \frac{{2{k_h} - \beta {k_h} + 3\beta {k_l} + 4{k_h}{k_l}}}{{2\left( {\beta + 2{k_h}} \right) }} - \frac{{\varDelta (3\beta + 4{k_h})}}{{2(\beta + 2{k_h})}}\sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}, \frac{{ - 2{k_h} + \beta {k_h}}}{\beta } + \frac{{3\beta + 4{k_h}}}{{2\beta }}\sqrt{\frac{{\left( {1 - \beta } \right) {k_h}}}{{\beta + {k_h}}}} \}$. When $\beta =0$, $c_g^I=\max \{0,0\}=0$.

When $\frac{{4{\varDelta ^2} - 4{k_l}^2}}{{1 + 4{\varDelta ^2} + 4{k_l}}}\le \beta < \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, the condition for Firm 1 to apply this response is ${p_2} \ge \frac{{{k_h}\left( {1 - \beta } \right) \left( {1 + {k_h}} \right) }}{{\beta \left( {1 - {k_h}} \right) + 2{k_h}}}$, which is always met when Firm 2 chooses his high price response. Then the condition for this equilibrium is ${c_g} >{\widetilde{{c_g^I}}}=\frac{{2{k_h} - \beta {k_h} + 3\beta {k_l} + 4{k_h}{k_l}}}{{2\left( {\beta + 2{k_h}} \right) }} - \frac{{\varDelta (3\beta + 4{k_h})}}{{2(\beta + 2{k_h})}}\sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}$. When $\beta > \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, the condition for Firm 1 to apply this response is ${p_2} \ge \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$, which is met when ${c_g} > \frac{{{k_h} - 2\beta {k_h} - 2k_h^2 + 3\beta {k_l} + 4{k_h}{k_l}}}{{\beta + 2{k_h}}}$.

More importantly, the cost threshold to sell the green product to green segment is ${c_g} < \frac{{{k_h} + \beta {k_h} + 2k_h^2}}{{\beta + 2{k_h}}}$ which is constraint by $p_2<{k_h}+p_1$. Then, when $\beta > \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, the equilibrium does not exist, because the feasible region is always higher than the cost threshold.

Case 2: When $p_2 < k_l+p_1$, if $p_2\ge (1+ k_h)p_1$, $p_2=\frac{{{c_g} + {p_1}}}{2} + \frac{{{k_l}{k_h}}}{{2({k_h} - \beta \varDelta )}}$ and $p_1=\frac{{{p_2}\left( {{k_h} - \beta \varDelta } \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }}$ intersect at

$$\begin{aligned} {p_1}= & {} \frac{{{c_g}{k_h} - \beta {c_g}\varDelta + {k_h}{k_l}}}{{3{k_h} - 3\beta \varDelta + 4{k_h}{k_l}}}\\ {p_2}= & {} \frac{{2\left( {{k_h} - \beta \varDelta + {k_h}{k_l}} \right) }}{{{k_h} - \beta \varDelta }}{p_1} \end{aligned}$$

Profits in equilibrium is given as:

$$\begin{aligned} {\varPi _1}= & {} \frac{{\left( {{k_h} - \beta \varDelta + {k_h}{k_l}} \right) {{\left( {{k_h}{k_l} + {c_g}({k_h} - \beta \varDelta )} \right) }^2}}}{{{k_h}{k_l}{{\left( {3{k_h} - 3\beta \varDelta + 4{k_h}{k_l}} \right) }^2}}}\\ {\varPi _2}= & {} \frac{{{{\left( { - 2{k_h}{k_l}\left( {{k_h} - \beta \varDelta + {k_h}{k_l}} \right) + {c_g}\left( {\left( { - 1 + \beta } \right) k_h^2\left( { - 1 + \beta - 2{k_l}} \right) + {\beta ^2}k_l^2 + 2\beta {k_h}{k_l}\left( {1 - \beta + {k_l}} \right) } \right) } \right) }^2}}}{{{k_h}{k_l}\left( {{k_h} - \beta \varDelta } \right) {{\left( {3{k_h} - 3\beta \varDelta + 4{k_h}{k_l}} \right) }^2}}} \end{aligned}$$

Constraint for Firm 2 to use the price regime is met when ${c_g} <c_g^1$ where

$$\begin{aligned} c_g^1=\frac{{{k_l}\left( {4{k_h} + 3\beta \varDelta + 4{k_l}{k_h}} \right) }}{{2\left( {{k_h} - \beta \varDelta + {k_l}{k_h}} \right) }} - \frac{{\varDelta (3{k_h} - 3\beta \varDelta + 4{k_l}{k_h})}}{{2\left( {{k_h} - \beta \varDelta + 2{k_l}{k_h}} \right) }}\sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}} \end{aligned}$$

Constraint for Firm 1 to use the price regime ${p_2} < \frac{{2{k_l}({k_h} - \beta \varDelta + {k_l}{k_h})}}{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}$ is met when ${c_g} < c_g^2$, where

$$\begin{aligned} c_g^2=\frac{{{k_l}\left( {3{\beta ^2}k_l^2 + \beta {k_h}{k_l}\left( {5 - 6\beta + 4{k_l}} \right) + k_h^2\left( {2 - 5\beta + 3{\beta ^2} + \left( {2 - 4\beta } \right) {k_l}} \right) } \right) }}{{\left( { - 1 + \beta } \right) k_h^2\left( { - 1 + \beta - 2{k_l}} \right) + {\beta ^2}k_l^2 + 2\beta {k_h}{k_l}\left( {1 - \beta + {k_l}} \right) }} \end{aligned}$$

We define ${c_g^{II}}=\min \{ c_g^1,c_g^2\}$, then $c_g<{c_g^{II}}$ is the condition for the existence of the Nash equilibrium in this price region. Comparing the cost thresholds we find that the inequality ${c_g^{II}}<{c_g^I}$ always holds. Then the equilibriums in Case 1 and 2 do not exist simultaneously.

There exists no other price equilibrium. Except the two Nash equilibriums, Firm 2 would only possible to price in his Case 4, where Firm 1 will always find his profit in this price region is suboptimal. Therefore, if ${k_l}< \varDelta$, there exist two Nash equilibriums as given in Case 1 and Case 2.

Case 3: ${p_{2}}=(1+ k_h)p_1$ and ${p_{1}}={p_{2}}-{k_{l}}$ intersect at $({p_{1}},{p_{2}})=(\frac{{{k_l}}}{{{k_h}}},{k_l}\mathrm{{ + }}\frac{{{k_l}}}{{{k_h}}})$.

$$\begin{aligned} {\varPi _1}= & {} A(1 - \beta )\left( 1 - \frac{{{k_l}}}{{{k_h}}}\right) \frac{{{k_l}}}{{{k_h}}}\\ {\varPi _2}= & {} A\beta \left( 1 - \frac{{{k_l}}}{{{k_h}}}\right) \left( {k_l}\mathrm{{ + }}\frac{{{k_l}}}{{{k_h}}} - {c_g}\right) \end{aligned}$$

Constraint for Firm 1 is met when $\beta < \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$. Otherwise, Firm 1 does not choose to price at ${p_{1}}={p_{2}}-{k_{l}}$ . For Firm 2, constraints of $p_1$ is met when $\frac{{\left( {1 + {k_h}} \right) {k_l}\left( {1 - \beta + {k_h} - 2\beta \varDelta } \right) }}{{{k_h}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) }}< {c_g} < \frac{{{k_l}\left( {{k_h}\left( {1 + {k_h}} \right) - \beta \varDelta + 2\beta {k_h}\varDelta } \right) }}{{{k_h}\left( {{k_h} - \beta \varDelta } \right) }}$. Then, under this cost condition and $\beta < \frac{{{\varDelta ^2} - {k_l}^2}}{{{k_h}^2 + {k_l} - {k_h}{k_l}}}$, the Nash equilibrium exists. This Nash equilibrium is different to the one in Case 2 that whether green consumers will purchase the traditional product. In Case 2, traditional products are sold to both segments; in Case 3, traditional products are sold to the primary segment only. $\square$

1.4 Nash equilibrium if $\varDelta <{k_l}$

Proof

When ${k_l}>\varDelta$, the candidate solutions are the same as given in the situation ${k_l}<\varDelta$, we check the constraint to give the feasible regions. When $p_2\ge k_l+p_1$, and $p_2\ge (1+ k_h)p_1$, the constraint of Firm 2’s decision ${p_1}$ does not change. For Firm 1 to price at Case 1, constraint ${p_2} \ge \frac{{{k_h} - \beta \varDelta + \beta {k_l} + 2{k_l}{k_h}}}{{\beta + 2{k_h}}}$ is met when ${c_g} > \frac{{{k_h} - 2\beta {k_h} - 2k_h^2 + 3\beta {k_l} + 4{k_h}{k_l}}}{{\beta + 2{k_h}}}$. Note that this condition is violated with the condition ${c_g} < \frac{{{k_h} + \beta {k_h} + 2k_h^2}}{{\beta + 2{k_h}}}$ which is obtained by the constraint by $p_2<{k_h}+p_1$. Then, there is no equilibrium exist in this price region $p_2\ge k_l+p_1$ and $p_2\ge (1+ k_h)p_1$. The equilibrium $({p_{1}},{p_{2}})=(\frac{{{k_l}}}{{{k_h}}},{k_l}\mathrm{{ + }}\frac{{{k_l}}}{{{k_h}}})$ does not exist either, because the constraint of Firm 1 is always violated. The constraint does not change in the equilibrium where the green product is sold to both segments. Therefore, when ${k_l}>\varDelta$, the only Nash equilibrium is:

$$\begin{aligned} {p_1}= & {} \frac{{{c_g}{k_h} - \beta {c_g}\varDelta + {k_h}{k_l}}}{{3{k_h} - 3\beta \varDelta + 4{k_h}{k_l}}}\\ {p_2}= & {} \frac{{2\left( {{k_h} - \beta \varDelta + {k_h}{k_l}} \right) }}{{{k_h} - \beta \varDelta }}{p_1} \end{aligned}$$

The Nash equilibrium exists when $c_g<{c_g^{II}}$. Otherwise, no equilibrium exists. $\square$

Proof of Corollary 4

Proof

The profit functions are given in C. It is easy to get the first order conditions of the functions and specially, at the equilibrium in C.3, we give the optimal $\beta$ at which Firm 2’ get his maximize profit.

$$\begin{aligned} \beta ^* = \frac{{ - 3{k_h} - 6{c_g}{k_h} + 6k_h^2 + \sqrt{3} {k_h}\sqrt{3 + 28{c_g} - 20c_g^2 - 28{k_h} + 40{c_g}{k_h} - 20k_h^2} }}{{6\left( {{c_g} - {k_h}} \right) }} \end{aligned}$$

$\square$

Proof of Proposition 4

Proof

Case 1: Now suppose Firm 1 anticipates the later entry and when ${p_1} \le {p_1^I}$, Firm 1’s objective is:

$$\begin{aligned} \mathop {\max }\limits _{{p_1}} {\varPi _1}\left( {{p_1}, {p_{2\left( {{p_1}} \right) }}} \right) = A\left( {1 - \beta - {p_1} + \beta \frac{{{p_{2\left( {{p_1}} \right) }} - {p_1}}}{{{k_h}}}} \right) {p_1} \end{aligned}$$

(48)

The optimal solution for the unconstrained problem is ${p_1} = {\frac{{\beta \left( {{c_g} - {k_h}} \right) + 2{k_h}}}{{2\left( {\beta + 2{k_h}} \right) }}}$ and ${\varPi _1} = \frac{{{{\left( {\beta {c_g} + \left( {2 - \beta } \right) {k_h}} \right) }^2}}}{{8{k_h}\left( {\beta + 2{k_h}} \right) }}$. Constraint ${p_1} \le {p_1^I}$ is satisfied when ${c_g} > c_g^{III} \buildrel \textstyle .\over = \frac{{2{k_h} + 4{k_h}{k_l}\mathrm{{ + }}\beta \left( {\varDelta - {k_l}} \right) }}{{\beta + 4{k_h}}} - 2\frac{{\varDelta \left( {\beta + 2{k_h}} \right) }}{{\beta + 4{k_h}}}\sqrt{\frac{{\beta {k_l}}}{{{k_h} - \beta \varDelta }}}$. Then Firm 1’s optimal price is given by:

$$\begin{aligned} {p_{1}} =\left\{ {\begin{array}{*{20}{ll}} {{\frac{{\beta \left( {{c_g} - {k_h}} \right) + 2{k_h}}}{{2\left( {\beta + 2{k_h}} \right) }}},}&{} \quad \mathrm{if} \,\,{c_g} > c_g^{III} ,\\ {{p_1^I}, }&{} \quad \mathrm{otherwise}.\ \end{array}} \right. \end{aligned}$$

(49)

The cost threshold is ${c_g} < {k_h} + \frac{{2{k_h}}}{{\beta + 4{k_h}}}$ to met the constraint ${p_2} < {k_h} + {p_1}$. In this cost condition,

$$\begin{aligned} \frac{{d{\varPi _1}}}{{d\beta }}= & {} \frac{{\left( {\beta {c_g} + \left( {2 - \beta } \right) {k_h}} \right) \left( {{c_g}\left( {\beta + 4{k_h}} \right) - {k_h}\left( {2 + \beta + 4{k_h}} \right) } \right) }}{{8{k_h}{{\left( {\beta + 2{k_h}} \right) }^2}}}<0\\ \frac{{d{\varPi _1}}}{{d{k_h}}}= & {} \frac{{\beta \left( {\beta {c_g} + \left( {2 - \beta } \right) {k_h}} \right) \left( {\left( {2 - \beta } \right) {k_h} - {c_g}\left( {\beta + 4{k_h}} \right) } \right) }}{{8k_h^2{{\left( {\beta + 2{k_h}} \right) }^2}}}<0 \end{aligned}$$

Case 2: When ${p_1^I} <{p_1} \le \frac{{{c_g}\left( {{k_h}- \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}$, Firm 1 does not deter Firm 2’s encroachment on primary segment, Firm 1’ objective is:

$$\begin{aligned} \mathop {\max }\limits _{{p_1}} {\varPi _1}\left( {{p_1},{p_{2\left( {{p_1}} \right) }}} \right) =A \left( { - {p_1} + \beta \frac{{{p_{2\left( {{p_1}} \right) }} - {p_1}}}{{{k_h}}} + \left( {1 - \beta } \right) \frac{{{p_{2l\left( {{p_1}} \right) }} - {p_1}}}{{{k_l}}}} \right) {p_1} \end{aligned}$$

(50)

The optimal solution for the unconstrained problem is ${p_{1}} = \frac{{{k_l}{k_h} + {c_g}\left( {{k_h} - \beta \left( {{k_h} - {k_l}} \right) } \right) }}{{2\left( {{k_h} - \beta \left( {{k_h} - {k_l}} \right) + 2{k_l}{k_h}} \right) }}$ and ${\varPi _1} = \frac{{{{\left( {{k_h}{k_l} + {c_g}\left( {{k_h} - \beta \varDelta } \right) } \right) }^2}}}{{8{k_h}{k_l}\left( {{k_h} - \beta \varDelta + 2{k_h}{k_l}} \right) }}$ . Constraint ${p_1} \le \frac{{{c_g}\left( {{k_h}- \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }}$ is always met. Constraint ${p_1} > {p_1^I}$ is satisfied when ${c_g} < c_g^{IV} \buildrel \textstyle .\over = \frac{{{k_l}\left( {3{k_h} - 2\beta \varDelta + 4{k_l}{k_h}} \right) }}{{{k_h} - \beta \varDelta + 4{k_l}{k_h}}} - 2\varDelta \frac{{{k_h} - \beta \varDelta + 2{k_l}{k_h}}}{{{k_h} - \beta \varDelta + 4{k_l}{k_h}}}\sqrt{\frac{{\beta {k_l}}}{{\left( {{k_h} - \beta \varDelta } \right) }}}$. When $\beta = 0$, $c_{L\left| {\beta = 0} \right. }^{IV} = \frac{{{k_l}\left( {3 + 4{k_l}} \right) }}{{1 + 4{k_l}}} = {k_l} + \frac{{2{k_l}}}{{1 + 4{k_l}}}$. Then firm 1’s optimal price is given by:

$$\begin{aligned} \small {p_{1}}= & {} \left\{ {\begin{array}{*{20}{ll}} {\frac{{{k_h}{k_l} + {c_g}\left( {{k_h} - \beta \varDelta } \right) }}{{2({k_h} - \beta \varDelta + 2{k_h}{k_l})}},}&{} \quad \mathrm{if} \,\,{c_g} < c_g^{IV} ,\\ { {p_1^I}, }&{} \quad \mathrm{otherwise}.\ \end{array}} \right. \nonumber \\ \frac{{d{\varPi _1}}}{{d\beta }}= & {} \frac{{\varDelta \left( {{k_h}{k_l} + {c_g}\left( {{k_h} - \beta \varDelta } \right) } \right) \left( {{k_h}{k_l} - {c_g}\left( {{k_h} - \beta \varDelta + 4{k_h}{k_l}} \right) } \right) }}{{8{k_h}{k_l}{{\left( {{k_h} - \beta \varDelta + 2{k_h}{k_l}} \right) }^2}}}\nonumber \\ \frac{{d{\varPi _1}}}{{d{k_h}}}= & {} \frac{{\beta \left( {{k_h}{k_l} + {c_g}\left( {{k_h} - \beta \varDelta } \right) } \right) \left( {{k_h}{k_l} - {c_g}({k_h} - \beta \varDelta + 4{k_h}{k_l})} \right) }}{{8k_h^2{{\left( {{k_h} - \beta \varDelta + 2{k_h}{k_l}} \right) }^2}}} \end{aligned}$$

(51)

Then $\frac{{d{\varPi _1}}}{{d\beta }}>0$ and $\frac{{d{\varPi _1}}}{{d{k_h} }}>0$ when ${c_g} < \frac{{{k_h}{k_l}}}{{{k_h} - \beta \varDelta + 4{k_h}{k_l}}}$. In this situation, green cost is so low that a growing $\beta$ and ${k_h}$, will leading to an equilibrium that Firm 1’s profit increases.

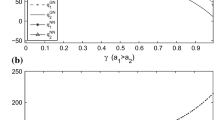
when $\frac{{{k_h}{k_l}}}{{{k_h} - \beta \varDelta + 4{k_h}{k_l}}}\le {c_g}< c_g^{IV}$, $\frac{{d{\varPi _1}}}{{d\beta }}\le 0$ and $\frac{{d{\varPi _1}}}{{d{k_h} }}\le 0$ . Here we use $\varPi _1^H$ and $\varPi _1^L$ to denote the profits when $p_1=\frac{{{k_l}{k_h} + {c_g}\left( {{k_h} - \beta \left( {{k_h} - {k_l}} \right) } \right) }}{{2\left( {{k_h} - \beta \left( {{k_h} - {k_l}} \right) + 2{k_l}{k_h}} \right) }}$ and the profit when $p_1={p_1^I}$, respectively. Comparing the profits of two price decisions we can obtain $\tilde{\beta }_3$. The exact characterization of $\tilde{\beta }_3$ is very hard but we show the existence of such $\tilde{\beta }_3$ via Fig. 5 assuming that ${k_h}=0.15$, ${k_l}=0.1$ and ${c_g}=0.16$. $\tilde{\beta }_3 \approx 0.18$.

Fig. 5

$\tilde{\beta }_3$ exists when Firm 1 compares his profits in different deterrence decisions

Cases 3 and 4: When $\frac{{{c_g}\left( {{k_h} - \beta \varDelta } \right) + {k_l}{k_h}}}{{\left( {{k_h} - \beta \varDelta } \right) \left( {1 + 2{k_h}} \right) }} < {p_1} \le \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_l}\left( {1 + {k_h}} \right) }}{{\left( {1 - \beta + 2{k_h} - 2\beta \varDelta } \right) \left( {1 + {k_h}} \right) }}$, Firm 1’s profit is $\frac{{\left( {1 - \beta } \right) \left( {{k_h} - {k_l}} \right) p_1^2}}{{{k_l}}}$ which is increasing in $p_1$, so Firm 1 get his optimal price at the boundary. When ${p_1} > \frac{{{c_g}\left( {1 - \beta + {k_h} - \beta \varDelta } \right) - {k_l}\left( {1 + {k_h}} \right) }}{{\left( {1 - \beta + 2{k_h} - 2\beta \varDelta } \right) \left( {1 + {k_h}} \right) }}$, the optimal price of the unconstraint problem is:

$$\begin{aligned} {p_1} = \frac{{ - \left( {1 + {k_h}} \right) {k_l} + {c_g}\left( { - 1 + \beta + \left( { - 1 + \beta } \right) {k_h} - \beta {k_l}} \right) }}{{2\left( { - 1 + \beta - 2{k_l} - 2\beta k_l^2 + \left( { - 1 + \beta } \right) {k_h}\left( {1 + 2{k_l}} \right) } \right) }} \end{aligned}$$

(52)

This solution can be optimal to the solution in Case 2 only when the profit in this case is higher than that in Case 2. $\square$

Proof of Corollary 4

Proof

The profits of Firm 1 have been discussed in E, we now discuss Firm 2’s profits at different equilibriums.

When $p_{_1}^ * = \frac{{\beta {c_g} + 2{k_h} - \beta {k_h}}}{{2\left( {\beta + 2{k_h}} \right) }}$, or $p_{_1}^ * ={p_1^I}$, Firm 2’s profit is increasing in $\beta$ and $k_h$.

When $p_{_1}^ * = \frac{{\beta {c_g} + 2{k_h} - \beta {k_h}}}{{2\left( {\beta + 2{k_h}} \right) }}$, Firm 2’s profit is: ${\varPi _\mathrm{{2}}} = \frac{{\beta {{\left( {{c_g}\left( {\beta + 4{k_h}} \right) - {k_h}\left( {2 + \beta + 4{k_h}} \right) } \right) }^2}}}{{16{k_h}{{\left( {\beta + 2{k_h}} \right) }^2}}}$. From the first order conditions we know Firm 2’s profit is increasing in ${k_h}$, but concave in $\beta$. $\frac{{d{\varPi _\mathrm{{2}}}}}{{d\beta }} = 0$ when

$$\begin{aligned} {\beta ^ * } = \frac{{ - {k_h} - {c_g}{k_h} + k_h^2 + \sqrt{k_h^2 + 6{c_g}k_h^2 - 7c_g^2k_h^2 - 6k_h^3 + 14{c_g}k_h^3 - 7k_h^4} }}{{{c_g} - {k_h}}} \end{aligned}$$

The second order condition $\frac{{{d^2}{\varPi _\mathrm{{2}}}}}{{d{\beta ^2}}}<0$ always holds. $\square$