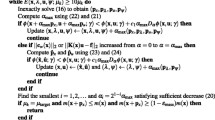Abstract
Free Material Optimization (FMO) is a branch of structural optimization in which the design variable is the elastic material tensor that is allowed to vary over the design domain. The requirements are that the material tensor is symmetric positive semidefinite with bounded trace. The resulting optimization problem is a nonlinear semidefinite program with many small matrix inequalities for which a special-purpose optimization method should be developed. The objective of this article is to propose an efficient primal-dual interior point method for FMO that can robustly and accurately solve large-scale problems. Several equivalent formulations of FMO problems are discussed and recommendations on the best choice based on the results from our numerical experiments are presented. Furthermore, the choice of search direction is also investigated numerically and a recommendation is given. The number of iterations the interior point method requires is modest and increases only marginally with problem size. The computed optimal solutions obtain a higher precision than other available special-purpose methods for FMO. The efficiency and robustness of the method is demonstrated by numerical experiments on a set of large-scale FMO problems.









Similar content being viewed by others
Notes
This assumption is standard within structural optimization. In the implementation it is satisfied by forcing that \(E_i\succeq \varepsilon I\) for some small \(\varepsilon >0\).
References
Achtziger, W., Bendsøe, M., Ben-Tal, A., Zowe, J.: Equivalent displacement based formulations for maximum strength truss topology design. Impact Comput. Sci. Eng. 4, 315–345 (1992)
Alizadeh, F., Haeberly, J., Overton, M.: Primal-dual interior-point methods for semidefinite programming: convergence rates, stability and numerical results. SIAM J. Opt. 8(3), 746–768 (2009)
Bendsøe, M., Díaz, A.: Optimization of material properties for Mindlin plate design. Struct. Opt. 6, 268–270 (1993)
Bendsøe, M., Guedes, J., Haber, R., Pedersen, P., Taylor, J.: An analytical model to predict optimal material properties in the context of optimal structural design. J. Appl. Mech. 61, 930–937 (1994)
Benson, H., Shanno, D.: Interior-point methods for nonconvex nonlinear programming: regularization and warmstarts. Comput. Opt. Appl. 40, 143–189 (2008)
Ben-Tal, A., Nemirovski, A.: Robust truss topology design via semidefinite programming. SIAM J. Opt. 7(4), 991–1016 (1997)
Ben-Tal, A., Kočvara, M., Nemirovski, A., Zowe, J.: Free material design via semidefinite programming: the multiload case with contact conditions. SIAM J. Opt. 9(4), 813–832 (1999)
Ben-Tal, A., Nemirovski, A.: Handbook of Semidefinite Programming, Structural Design. Kluwer Academic Publishers, Philip Drive Norwell, MA (2000)
Cook, R., Malkus, D., Plesha, M., Witt, R.: Concepts and Applications of Finite Element Analysis, 4th edn. John Wiley, Hoboken (2002)
Dolan, E., Moré, J.: Benchmarking optimization software with performance profiles. Math. Program. 97(A), 201–213 (2002)
Forsgren, A., Gill, P.: Primal-dual interior methods for nonconvex nonlinear programming. SIAM J. Opt. 8(4), 1132–1152 (1998)
Forsgren, A., Gill, P., Wright, M.: Interior methods for nonlinear optimization. SIAM Rev. 44(4), 525–597 (2002)
Gaile, S.: Free material optimization for shells and plates. Ph.D. thesis, Institute of Applied Mathematics II, Friedrich–Alexander University of Erlangen–Nuremberg (2011)
Golub, G., Van Loan, C.: Matrix Comput., 3rd edn. Johns Hopkins University Press, Baltimore (1996)
Haslinger, J., Kočvara, M., Leugering, G., Stingl, M.: Multidisciplinary free material optimization. SIAM J. Appl. Math. 70(7), 2709–2728 (2010)
Helmberg, C., Rendl, F., Vanderbei, R., Wolkowicz, H.: An interior-point method for semidefinite programming. SIAM J. Opt. 6, 342–361 (1996)
Kočvara, M., Stingl, M.: PENNON a code for convex nonlinear and semidefinite programming. Opt. Methods Softw. 18(3), 317–333 (2003)
Kočvara, M., Stingl, M.: Free material optimization for stress constraints. Struct. Multidiscip. Opt. 33, 323–335 (2007)
Kočvara, M., Stingl, M., Zowe, J.: Free material optimization: recent progress. Optimization 57(1), 79–100 (2008)
Kojima, M., Shindoh, S., Hara, S.: Interior-point methods for the monotone semidefinite linear complementarity problem in symmetric matrices. SIAM J. Opt. 7(1), 86–125 (1997)
Monteiro, R.: Primal-dual path-following algorithms for semidefinite programming. SIAM J. Opt. 7(3), 663–678 (1997)
Monteiro, R.: First- and second-order methods for semidefinite programming. Math. Program. 97, 209–244 (2003)
Nesterov, Y., Todd, M.: Self-scaled barriers and interior-point methods for convex programming. Math. Oper. Res. 22(1), 1–42 (1997)
Nesterov, Y., Todd, M.: Primal-dual interior-point methods for self-scaled cones. SIAM J. Opt. 8(2), 324–364 (1998)
Ringertz, U.: On finding the optimal distribution of material properties. Struct. Opt. 5, 265–267 (1993)
Stingl, M.: On the solution of nonlinear semidefinite programs by augmented lagrangian method. Ph.D. thesis, Institute of Applied Mathematics II, Friedrich–Alexander University of Erlangen–Nuremberg (2006). http://www2.am.uni-erlangen.de/
Stingl, M., Kočvara, M., Leugering, G.: Free material optimization with fundamental eigenfrequency constraints. SIAM J. Opt. 20(1), 524–547 (2009)
Stingl, M., Kočvara, M., Leugering, G.: A new non-linear semidefinite programming algorithm with an application to multidisciplinary free material optimization. Int. Ser. Numer. Math. 158, 275–295 (2009)
Stingl, M., Kočvara, M., Leugering, G.: A sequential convex semidefinite programming algorithm with an application to multiple-load free material optimization. SIAM J. Opt. 20(1), 130–155 (2009)
Todd, M.: A study of search directions in primal-dual interior-point methods for semidefinite programming. Opt. Methods Softw. 11, 1–46 (1999)
Todd, Y., Toh, K., Tütüncü, R.: On the Nesterov–Todd direction in semidefinite programming. SIAM J. Opt. 8(3), 769–796 (1998)
Vogelbusch, C.H.: Numerical treatment of nonlinear semidefinite programs. Ph.D. thesis, Institut für Mathematik der Heinrich–Heine–Universität Düsseldorf (2006). http://docserv.uni-duesseldorf.de/
Waltz, R., Morales, J., Nocedal, J., Orban, D.: An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 107, 391–408 (2006)
Werner, R.: Free material optimization-mathematical analysis and numerical solution. Ph.D. thesis, Institute of Applied Mathematics II, Friedrich–Alexander University of Erlangen–Nuremberg (2001)
Yamashita, H., Yabe, H., Harada, K.: A primal-dual interior point method for nonlinear semidefinite programming. Math. Program. 135, 89–121 (2012)
Zhang, Y.: On extending some primal-dual interior-point algorithms from linear programming to semidefinite programming. SIAM J. Opt. 8(2), 365–386 (1998)
Zowe, J., Kočvara, M., Bendsøe, M.: Free material optimization via mathematical programming. Math. Program. 79, 445–466 (1997)
Acknowledgments
The authors would like to thank two reviewers for their constructive and insightful comments and suggestions. We also would like to express our gratitude to our former colleague Stefanie Gaile for many and fruitful discussions on Free Material Optimization. The research was partially funded by the Danish Council for Strategic Research through the Danish Center for Composite Structures and Materials (DCCSM).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
In this Appendix we derive the dual formulation (8) of the minimum weighted compliance problem (3). Similar result for minimax problems can be found in [7]. Analogous all-quadratic formulations of minimum compliance truss topology optimization problems are described, for example, in [1]. The linear elasticity static structural analysis problem can be written as
which is a quadratic problem with negative definite Hessian and hence a concave maximization problem. The optimality condition is \(A(E)u_\ell =f_\ell \) and the optimal value is \(f_\ell ^Tu_\ell \) if \(f_\ell \in \mathcal {R}(A(E))\) and \(-\infty \) otherwise. Due to the stated assumptions we replace the \(\sup \) with \(\max \) in the following. Therefore, the minimum compliance problem (3) is equivalent to

The Lagrangian \(\mathcal {L}\) associated with (42) is
The corresponding dual function is
Below is the condition that the dual function \(g\) attains its minimum value.
The dual formulation of the minimum compliance problem (3) becomes
Appendix 2
The following products are in tensor notation.
-
1.
\((\nabla _{X_rX_s}^2\mathcal {L}_\mu (X,u,s,\lambda )\varDelta X_s)_{ij}=(\nabla _{X_rX_s}^2\mathcal {L}_\mu (X,u,s,\lambda ))_{ijpq}(\varDelta X_s)_{pq}\), for \(r,s=1,\ldots ,m\), for \(i,j=1,\ldots ,d_r\), and for \(p,q=1,\ldots ,d_s\).
-
2.
\((\nabla _{X_ru}^2\mathcal {L}_\mu (X,u,s,\lambda )\varDelta X_r)_{i}\!=\!(\nabla _{uX_r}^2\mathcal {L}_\mu (X,u,s,\lambda ))_{ipq}(\varDelta X_r)_{pq}\), for \(r\!=\!1,\ldots ,m\), for \(p,q=1,\ldots ,d_r\), and for \(i=1,\ldots ,n\).
-
3.
\((\nabla _{X_ru}^2\mathcal {L}_\mu (X,u,s,\lambda )^T\varDelta u)_{ij}=(\nabla _{X_ru}^2\mathcal {L}_\mu (X,u,s,\lambda ))_{ijp}(\varDelta u)_{p}\), for \(r=1,\ldots ,m\), for \(i,j=1,\ldots ,d_r\), and for \(p=1,\ldots ,n\).
-
4.
\((\nabla _{X_r}g(X,u)^T\varDelta \lambda )_{ij}=(\nabla _{X_r}(g(X,u)^T\varDelta \lambda ))_{ij}\), for \(r=1,\ldots ,m\), and for \(i,j=1,\ldots ,d_r\).
-
5.
\((\nabla _{X_r}g(X,u)\varDelta X_r)_i=(\nabla _{X_r}g_i(X,u))_{pq}(\varDelta X_r)_{pq}\), for \(r=1,\ldots ,m\), for \(p,q=1,\ldots ,d_r\), and for \(i=1,\ldots ,k\).
Rights and permissions
About this article
Cite this article
Weldeyesus, A.G., Stolpe, M. A primal-dual interior point method for large-scale free material optimization. Comput Optim Appl 61, 409–435 (2015). https://doi.org/10.1007/s10589-014-9720-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-014-9720-6