Abstract
We study a family of voting rules inspired by the peculiar protocol used for over 500 years by the Republic of Venice to elect its Doge. Lot-based indirect elections have two main features: a pool of delegates is chosen by lot out of a general assembly, and then they vote in a single winner election with qualified majority. Under the assumption that the assembly is divided into two factions, we characterise the win probability of the minority and show that these features promote a more equitable allocation of political representation, striking a balance between protecting the minority and giving proper recognition to the majority. We then consider this family of voting procedures from a constitutional perspective: we analyse how the electoral result varies with the college size and the winning threshold in order to understand how these two parameters can be tuned when drawing up electoral law. We find that minorities are better off with larger majority thresholds. The role of the college size, on the other hand, is ambiguous: a smaller college size offers more protection to sparse minorities; for more sizeable ones, it depends instead on the qualified majority required for the election.




Similar content being viewed by others
Notes
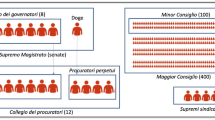
In 1273, Venice adopted a two-round protocol to elect magistrates. An initial group of forty, chosen at random from the Great Council, was reduced by lot to a committee of nine people who elected each magistrate with a qualified majority of six out of nine. The use of iterations was later extended to magistrates’ elections (Tucci 1982: 91). The usage of two consecutive uniform random draws in both the magisterial and the dogal election protocols is commonly viewed as a practical solution to the problem of ensuring a genuine random lot over a constituency as large as the Great Council.
One of the earliest uses of a supermajority rule other than unanimity was the election of the Pope in 1179; selection by lot instead dates back to ancient Greece. Both were widely used in the Middle Ages. For a history of the two institutions see Chapter 3 of Schwartzberg (2014), Tridimas (2012) and Wolfson (1899).
When choosing over two alternatives, the approval voting used in the Venetian electoral protocol is equivalent to the case where each voter only casts one ballot.
In a single candidate election, ex-post proportional representation is impossible, except in the case of unanimity. However, it can be attained ex-ante when the probability of winning the seat reflects the distribution of votes. For a discussion of probabilistic proportional representation, see Amar (1984).
From Proposition 3 we already know that with the unanimity rule \((\tau =1)\) we get proportional representation for any college size.
References
Amar, A. R. (1984). Choosing representatives by lottery voting. Yale Law Journal, 93(7), 1283–1308.
Buchanan, J. M., & Tullock, G. (1962). The calculus of consent. Ann Arbor: University of Michigan Press.
Caplin, A., & Nalebuff, B. (1988). On 64%-majority rule. Econometrica, 56(4), 787–814.
Coggins, J. S., & Perali, C. F. (1998). 64% majority rule in ducal Venice: Voting for the Doge. Public Choice, 97(4), 709–723.
da Mosto, A. (1966). I dogi di Venezia nella vita pubblica e privata (2nd ed.). Milano: Aldo Martello Editore.
Finlay, R. (1980). Politics in Renaissance Venice. New Brunswick: Rutgers University Press.
Greif, A., & Laitin, D. D. (2004). A theory of endogenous institutional change. American Political Science Review, 98(4), 633–652.
Lines, M. (1986). Approval voting and strategy analysis: A Venetian example. Theory and Decision, 20(2), 155–172.
Maranini, G. (1927). La costituzione di Venezia. Dalle origini alla Serrata del Maggior Consiglio. [Reissued in 1974]. Firenze: La Nuova Italia.
Mowbray, M., & Gollmann, D. (2007). Electing the Doge of Venice: Analysis of a 13th century protocol. In Proceedings of the 20th IEEE computer security foundations symposium (pp. 295–310). IEEE Computer Society.
Mueller, D. C., Tollison, R. D., & Willett, T. D. (1972). Representative democracy via random selection. Public Choice, 12(1), 57–68.
Mulgan, R. G. (1984). Lot as a democratic device of selection. The Review of Politics, 46(4), 539–560.
Norwich, J. J. (1982). A history of Venice. [Reissued in 2003]. London: Penguin Books.
Schwartzberg, M. (2014). Counting the many: The origins and limits of supermajority rule. Cambridge: Cambridge University Press.
Tridimas, G. (2012). Constitutional choice in ancient Athens: The rationality of selection to office by lot. Constitutional Political Economy, 23(1), 1–21.
Tucci, U. (1982). I meccanismi dell’elezione dogale, reissued in 2014 in Venezia e dintorni. Evoluzioni e trasformazioni. Roma: Viella.
Walsh, T., & Xia, L. (2011). Venetian elections and lot-based voting rules. In E. Elkind, U. Endriss & J. Lang (Eds.), Proceedings of the IJCAI-2011 workshop on social choice and artificial intelligence (pp. 93–98).
Wolfson, A. M. (1899). The ballot and other forms of voting in the Italian communes. The American Historical Review, 5(1), 1–21.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author thanks Marco LiCalzi, Luciano Pezzolo, and two anonymous referees for useful comments. An earlier version of this paper circulated as WP 2018-2, Department of Economics, Ca’ Foscari University of Venice.
Appendix
Appendix
1.1 Proof of Proposition 1
Proof
First, consider \(x\le m\), which implies \(p_x> 0\). Then either \(y>m,\) in which case \(p_y=0\) and thus \(p_x>p_y=0\), or else \(y\le m\) and \(p_y\ne 0.\) In the latter case the definition of the binomial coefficient and \(y=c-x\) imply:
By an analogous reasoning we obtain:
We now use (2) and (3) to express \(p_x\) as a function of \(p_y\):
where the last inequality follows from the fact that, being \(m<n/2\), each fraction in the last line is greater than one.
Next, consider the case \(x> m.\) Since \(x<y,\) we have \(y>m\) and, therefore, \(p_x=p_y=0.\) This completes the proof. \(\square\)
1.2 Proof of Proposition 2
Proof
Suppose \(w=0\). Given the definition of w in (1), it must be \(p_x=0\) for any \(x\ge c-t+1\). But with the hypergeometric distribution \(p_x=0\) if and only if \(x>m\). It follows that \(m<c-t+1,\) a contradiction. \(\square\)
1.3 Proof of Proposition 3
Proof
First we prove that \(w\le \mu .\) Start with Eq. (1):
Add and subtract both \(\sum _{x=0}^{c-t}p_x\frac{x}{c}\) and \(\sum _{x=t}^{c}p_x\frac{x}{c}\) to get
For the hypergeometric distribution the expected value \(\sum _{x=0}^{c}p_x x\) is equal to \(\dfrac{m}{n}c\). Inserting this value in the equation above and rearranging the terms yields
We can simplify this expression and switch to a new summation index in the last term, yielding:
We now use Proposition 1 to sign the last term of this equality. By definition of supermajority threshold, \(t >\dfrac{c}{2}\). Then, for any value of \(x\in \{0, 1,\dots , c-t\}\), we know that \(x<c-x\). Since \(x+(c-x)=c\) the proposition applies and, thus, each term \((p_x-p_{c-x})\) in the sum is non-negative. This implies \(w\le \mu\).
To complete the proof consider \(t=c\). Then neither faction can be decisive and Eq. (4) reduces to
\(\square\)
1.4 Proof of Proposition 4
Proof
Fix n, m and c. Abusing notation, we drop these three parameters and write w[t] for the mwp given a value of the supermajority threshold \(t<c\). It is enough to show that when we raise the threshold from t to \(t+1\), the difference \(\Delta _t w=w[t+1]-w[t]\) is positive.
Using the definition of mwp given in Eq. (1) we write
Similarly, the winning probability for a threshold \(t+1\) is
Notice that all the terms in w[t] and \(w[t+1]\) are the same except for those indexed by \(c-t\) and t. Then the difference \(\Delta _t w\) reduces to:
To determine the sign of \(\Delta _t w\) notice that \(c-t\ge 0\) by definition of supermajority threshold. This implies that \(\Delta _t w\) has the same sign as \((p_{c-t}-p_t)\). Since the pair of probabilities \(p_{c-t}\) and \(p_t\) satisfies the conditions of Proposition 1 and we are computing w for a minority faction, we know that \((p_{c-t}-p_t)\ge 0\) and thus conclude that \(\Delta _t w\ge 0.\)
To complete the proof consider the unanimity rule. When \(t=c\) the mwp is:
where the last equality follows from the fact that the expected value \(\sum _{x=1}^{c}p_x\,x\) is equal to \(\dfrac{mc}{n}\) for a hypergeometric random variable. \(\square\)
Rights and permissions
About this article
Cite this article
Molinari, M.C. How the Republic of Venice chose its Doge: lot-based elections and supermajority rule. Const Polit Econ 31, 169–187 (2020). https://doi.org/10.1007/s10602-019-09290-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10602-019-09290-6