Three-way investment decisions during the epidemic with Choquet-based bi-projection method

Abstract

The outbreak of epidemic has had a big impact on the investment market of China. Facing the turbulence in the investment market, many enterprises find it difficult to judge the development prospects of investment projects and make the right investment decisions. The three-way decisions offer a novel study perspective to solve this problem. Then the developed model is applied to select the investment projects. Firstly, some relevant attributes of the project are described with the double hierarchy hesitant fuzzy linguistic term sets. And a double hierarchy hesitant fuzzy linguistic information system is constructed for each project. Secondly, the weights of attributes are determined with the Choquet integral method. And the closeness degree calculated by Choquet-based bi-projection method is taken as the conditional probability that the project will be profitable. Next, considering the influence of the bounded rationality of decision makers, the threshold parameters are calculated based on prospect theory. Finally, the decision results about investment projects during four stages are deduced based on the principle of maximum-utility, which demonstrates the practicability and effectiveness of the proposed model.

1 Introduction

Since the COVID-19 outbroke, we witnessed the tremendous impact of COVID-19 (Ena & Wenzel, 2020). The economy of China went from a shutdown to a gradual recovery (Lieke & Pierre, 2019). The investment market also experienced ups and downs, and started to recover after two shocks. Facing the turbulence in the investment market, many enterprises find it difficult to judge the development prospects of investment projects and make the right investment decisions. Therefore, it is important for enterprises to grasp the development prospect of investment projects through scientific and systematic analysis.

The three-way decisions (TWDs) offer a novel study perspective to solve this problem. Since TWDs was proposed by Yao et al. (1990) and Yao (2010), it had played an unique role in the research of decision theory. Intuitively, objects are divided into three disjoint regions (positive region, boundary region and negative region) by employing the Bayesian process (Yao et al., 1990). When an object is divided into the positive region, negative region or boundary region, it means that the decision maker should accept the object, and reject the object or delay the decision respectively. As the TWDs fit the human’s thinking patterns, it has been applied to many fields, such as medical treatment (Hu et al., 2018), risk decision making (Liang & Liu, 2015). In order to describe the loss functions in the TWDs better, many extended forms of fuzzy sets, such as fuzzy set (Ye et al., 2020), triangular fuzzy number (Liang et al., 2013), dual hesitant fuzzy set (Liang et al., 2017) have been introduced into the process of TWDs. As the other crucial element of TWDs, the calculation of conditional probability has been studied by many scholars. Ye et al. (2020) determined the weights of attributes by entropy weight method (Zhang & Zhou, 2008) firstly, and then calculated the conditional probability by weighted aggregation. Liang et al. (2018) determined the weights of attributes by maximizing deviation method (Wang, 1997) firstly, and then obtained the conditional probability by technique for order performance by similarity to an ideal solution (TOPSIS) (Zhang & Xu, 2014). Lei et al. (2020) designed behavioral TWDs model under hesitant fuzzy linguistic environment. In this study, the weights of attributes are determined by Choquet integral (Choquet, 1954; Tan, 2011). And then the conditional probability is calculated by the bidirectional projective method (Wang et al., 2020; Liu et al., 2014). It takes into account both the relationship between the scheme and the positive and negative ideal solutions, which makes the results of decision more objective.

In the description of the qualitative problem, the linguistic terms conform with people’s habits of expression more. Since Zadeh (2013) put forward the definition of Computing with Words and accounted for its meaning, various extension forms of linguistic term sets (LTSs) (Rodriguez et al., 2011) had been proposed and studied. To improve the accuracy of linguistic terms, Gou et al. (2017, 2018) defined double hierarchy linguistic term set (DHLTS). Combined with the merits of hesitant fuzzy sets, Gou et al. (2017) and Gou et al. (2019) developed double hierarchy hesitant fuzzy linguistic term sets (DHHFLTSs). In the process of projects investment, it is difficult for most investors to give an accurate assessment about the attributes of projects. And it is more convenient and appropriate for most investors to undertake qualitative evaluation to project attributes. In contrast to the single linguistic term set, DHHFLTSs provide more flexible manner to express qualitative information by means of linguistic expressions. When investors evaluate the information of attributes of the project, they can give the evaluation value more intuitively, which saves a lot of time for decision-making. Timely decisions are important to investors. It is also a kind of convenient and effective tool for investors, which help the investors make decisions more easily. The appearance of DHHFLTSs provides a novel tool for describing loss functions in TWDs.

The outbreak of COVID-19 has brought a huge shock to the investment market of China. The fiscal and monetary policies have also been adjusted and changed during the epidemic. It is both a challenge and an opportunity for enterprises. Faced with the rapid and dramatic changes in the investment market, many enterprises find it difficult to judge the development prospects of investment projects and make the proper investment decisions. Therefore, it is important for enterprises to grasp the development prospect of investment projects through scientific and systematic analysis. However, traditional multi-attribute decision making method only shows the comprehensive arrangement order of the scheme, rather than tell the decision maker how to make the right choice for each scheme. Therefore, it has certain limitations in solving the problem of investment scheme selection.

The TWDs meets the decision-making needs of enterprises. It offers the enterprise three options: invest in this project, reject the project, and gather more information before making a decision. Then, we apply the TWDs model to the selection of investment projects during the epidemic. Firstly, we construct the DHHFLT information system based on the attributes of investment projects. Secondly, the conditional probability is calculated by Choquet-based bi-projection method. Next, as a kind of convenient and effective tool, DHHFLTSs are used to describe the loss functions and the benefit functions in the process of TWDs. And based on different risk attitudes of investors, we introduce prospect theory (Kahneman & Tversky, 2013; Tversky & Kahneman, 1992) into the processing of benefit and loss functions. Finally, due to the profit purpose of enterprises, we obtain the decision-making results according to the maximum-utility principle.

On the basis of the above analysis, the merits of the proposed model are (1) The calculation of the conditional probability, by the bi-projection model, takes into account both the relationship between the scheme and the positive and negative ideal solutions. And it makes the results of decisions more objective. (2) The acquisition of the attributes weights, by the Choquet integral method, shows the association between attributes. And it is an appropriate method for investors to obtain the weights of attributes. (3) The processing of benefit and loss functions, by the prospect theory, takes into account different risk attitudes of investors. And it makes the process of decisions more rational.

The main content of this paper is organized as follows: Sect. 2 provides the basic concepts of DHHFLTSs, prospect theory and fuzzy measure. Section 3 discusses a novel DHHFL DTRS model based on prospect theory. Section 4 introduces the calculation process of conditional probability with Choquet-based bi-projection method. Section 5 designs a decision-making process of the model proposed by us. Section 6 illustrates the selection of investment projects during the epidemic. Section 7 shows the impact of using different values of the loss aversion factor by a sensitivity analysis. Section 8 compares our proposed model with the other models and discusses the advantages and limitations of the proposed model. Section 9 concludes the study and further elaborates its theoretical and applied value.

2 Preliminaries

In this section, some basic concepts of DHHFLTSs, prospect theory and fuzzy measure are introduced briefly.

2.1 Double hierarchy hesitant fuzzy linguistic term sets

In order to improve the accuracy of the expression of linguistic terms, Gou et al. (2017) defined the DHLTS.

Definition 2.1

(Gou et al., 2017) Given that $S=\{s_{t}|t=-\tau ,\ldots ,-1,0,1,\ldots ,\tau \}$ and $O=\{o_{k}|k=-\zeta ,\ldots ,-1,0,1,\ldots ,\zeta \}$ are the first and second hierarchy LTSs, respectively. Then, the mathematical form of DHLTS, $S_{o}$, is displayed as follows:

$$\begin{aligned} S_{o}=\{s_{t\langle o_{k}\rangle }|t=-\tau ,\ldots ,-1,0,1,\ldots ,\tau ;k=-\zeta ,\ldots ,-1,0,1,\ldots ,\zeta \}, \end{aligned}$$

(1)

among them, $s_{t\langle o_{k}\rangle }$ represents the DHLT, $s_{t}$ denotes the first hierarchy linguistic term, $o_{k}$ denotes the second hierarchy linguistic term.

It is worth noting that the order of the second hierarchy LTS needs to be shown on basis of the values of t.

Remark 2.1

(Gou et al., 2017) There are four types of propositions which are displayed based on different values of t: (1) If $t>0$, then the first hierarchy LTS is positive, and the second hierarchy LTS needs to be displayed in ascending order. (2) If $t<0$, then the first hierarchy LTS is negative, the second hierarchy LTS needs to be displayed in descending order inversely. (3) If $t=\tau$, then we just think about the front half of the second hierarchy LTS. (4) If $t=-\tau$, then we think about the latter half of the second hierarchy LTS.

In order to deal with DHLT easier, Gou et al. (2017) proposed two transformed functions between the numerical scale and the subscript of the DHLT.

Definition 2.2

(Gou et al., 2017) Given that ${\overline{S}}_{o}=\{s_{t\langle o_{k}\rangle }|t\in [-\tau ,\tau ];k\in [-\zeta ,\zeta ]\}$ is a continuous DHLTS, $h_{S_{o}}=\{s_{\phi _{l}<o_{\varphi _{l}}>}|s_{\phi _{l}<o_{\varphi _{l}}>}\in {\overline{S}}_{o};l=1,2,\ldots ,L;\phi _{l}\in [-\tau ,\tau ];\varphi _{l}\in [-\zeta ,\zeta ]\}$ is a double hierarchy hesitant fuzzy linguistic element (DHHFLE), and $h_{\gamma }=\{\gamma _{l}|\gamma _{l}\in [0,1];l=1,2,\ldots ,L\}$ is a set of numerical scales. There are a transformed function f between the numerical scale and the subscript $(\phi _{l},\varphi _{l})$ of the DHLT $s_{\phi _{l}<o_{\varphi _{l}}>}$:

$$\begin{aligned} f:[-\tau ,\tau ]\times [-\varsigma ,\varsigma ]\rightarrow [0,1], \end{aligned}$$

$$\begin{aligned} f(\phi _{l},\varphi _{l})=\frac{\varphi _{l}+(\tau +\phi _{l})\varsigma }{2\varsigma \tau }=\gamma _{l}. \end{aligned}$$

(2)

In light of Definition 2.2, we can develop the transformation function F between the DHLT $s_{\phi _{l}<o_{\varphi _{l}}>}$ and the numerical scale $\gamma _{l}$.

$$\begin{aligned} F: {\overline{S}}_{o}\rightarrow h_{\gamma }, F(s_{\phi _{l}<o_{\varphi _{l}}>})=f(\phi _{l},\varphi _{l})=\gamma _{l}. \end{aligned}$$

(3)

Taking into account the hesitant fuzzy situation, Gou et al. (2017) defined DHHFLTSs.

Definition 2.3

(Gou et al., 2017) Given that X is a fixed set, $H_{S_{o}}$ represents a DHHFLTS on X. It is defined by a membership function. The function applied to X returns a subset of ${\overline{S}}_{o}$, and its mathematical form is displayed as follows:

$$\begin{aligned} H_{S_{o}}=\{<x_{i},h_{S_{o}(x_{i})}>|x_{i}\in X\}, \end{aligned}$$

(4)

where $h_{S_{o}(x_{i})}$ is a set of some values in ${\overline{S}}_{o}$, expressed by

$$\begin{aligned} \begin{aligned}&h_{S_{o}}(x_{i})=\{s_{\phi _{l}<o_{\varphi _{l}}>}(x_{i})|s_{\phi _{l}<o_{\varphi _{l}}>}\in {\overline{S}}_{o};l=1,2,\ldots ,L;\phi _{l}\in [-\tau ,\tau ];\varphi _{l}\in [-\zeta ,\zeta ]\}, \end{aligned} \end{aligned}$$

(5)

among them, L represents the number of DHLT in $h_{S_{o}}(x_{i})$ and $s_{\phi _{l}<o_{\varphi _{l}}>}(x_{i})(l=1,2,\ldots ,L)$ in each $h_{S_{o}}(x_{i})$ are the continuous terms in ${\overline{S}}_{o}$. $h_{S_{o}}(x_{i})$ denotes the possible degree of the linguistic variable $x_{i}$ to ${\overline{S}}_{o}$. Then, we call $h_{S_{o}}(x_{i})$ the DHHFLE, and $\phi \times \psi$ denote the set of all DHHFLEs.

Next, Gou et al. (2019) developed the concept of linguistic expected-value.

Definition 2.4

(Gou et al., 2019) Given that $h_{S_{o}}=\{s_{\phi _{l}<o_{\varphi _{l}}>}|s_{\phi _{l}<o_{\varphi _{l}}>}\in {\overline{S}}_{o};l=1,2,\ldots ,L\}$ is a DHHFLE, $\phi \times \psi$ is the set of all DHHFLEs over ${\overline{S}}_{o}$. Then, we can obtain a linguistic expected-value of $h_{S_{o}}$ as follows:

$$\begin{aligned} le:\phi \times \psi \rightarrow {\overline{S}}_{o},le(h_{S_{o}})=\frac{1}{L} \bigoplus ^{L}_{l=1}s_{\phi _{l}<o_{\varphi _{l}}>}=s_{\frac{1}{L} \sum ^{L}_{l=1}\phi _{l}<o_{\frac{1}{L}\sum ^{L}_{l=1}\varphi _{l}}>}. \end{aligned}$$

(6)

It is usually used in the normalization process of DHHFLT information systems.

Example 2.1

An expert prepares to evaluate the innovation of three investment projects with DHHFLTS, $X=\{x_{1},x_{2},x_{3}\}$ denote a set of investment projects, $H_{S_{o}}=\{<x_{1},\{s_{1\langle o_{3}\rangle },s_{2\langle o_{1}\rangle }\}>,<x_{2},\{s_{0\langle o_{1}\rangle },s_{1\langle o_{1}\rangle }\}>,<x_{3},\{s_{-1\langle o_{0}\rangle },s_{0\langle o_{-1}\rangle }\}>\}$ is a DHHFLTS with $\tau =\zeta =4$, which represents the innovation degrees of three investment projects. And $h_{S_{o}}(x_{1})=\{s_{1\langle o_{3}\rangle },s_{2\langle o_{1}\rangle }\}, h_{S_{o}}(x_{2})=\{s_{0\langle o_{1}\rangle },s_{1\langle o_{1}\rangle }\}, h_{S_{o}}(x_{3})=\{s_{-1\langle o_{0}\rangle },s_{0\langle o_{-1}\rangle }\}$ are three DHHFLEs, then the linguistic expected-values of them are: $le(h_{S_{o}}(x_{1}))=\{s_{\frac{3}{2}\langle o_{2}\rangle }\},le(h_{S_{o}}(x_{2}))=\{s_{\frac{1}{2}\langle o_{1}\rangle }\},le(h_{S_{o}}(x_{3}))=\{s_{-\frac{1}{2}\langle o_{-\frac{1}{2}}\rangle }\}$. Based on the transformation function F, $F(le(h_{S_{o}}(x_{1})))=0.750, F(le(h_{S_{o}}(x_{2})))=0.594, F(le(h_{S_{o}}(x_{3})))=0.422$. Then the ranking result about the innovation of three investment projects is $x_{1}\succ x_{2} \succ x_{3}.$

2.2 Prospect theory

Prospect theory was put forward by Kahneman and Tversky (Kahneman & Tversky, 2013). Through experimental research, they found the common phenomenon that people’s actual decision-making behavior deviated from the expected utility theory under the risk condition. In order to explain and describe these behavioral biases well, they introduced the research results of psychology into economics and proposed the prospect theory. They divided the individual decision-making process under risk conditions into two phases: editing phase and evaluation phase. The edited prospects (Tversky & Kahneman, 1992) can be determined with the aid of a prospect value function as follows:

$$\begin{aligned} u(x)={\left\{ \begin{array}{ll}x^{\rho },\quad ( x\ge 0) \\ -\theta (-x)^{\delta },\quad (x<0)\\ \end{array}\right. }, \end{aligned}$$

(7)

among them, $\rho$ and $\delta$ represent the concavoconvex degree of value function in the gain and loss area respectively, reflecting the rate of sensitivity decline of decision maker. $0\le \rho ,\delta \le 1;$ $\theta$ reflects the degree of loss aversion of decision makers, which is used to indicate that the loss area of value function is steeper than the gain area. In light of the original research, Tversky and Kahneman (1992) assumed that $\rho =\delta =0.88$ and $\theta =2.25$, which is consistent with the empirical evidence afterwards.

2.3 Fuzzy measure

Choquet integral is an effective tool for dealing with situations where attributes are interrelated of each other.

Definition 2.5

(Choquet, 1954) Given that $X=\{x_{1},x_{2},\ldots ,x_{n}\}$ is a universe of discourse, P(X) is the power set of X. A fuzzy measure on X is a set function $r:P(X)\rightarrow [0,1]$, satisfying

(1) $r(\emptyset )=0, r(X)=1.$

(2) If $D,B\in P(X)$ and $D\subseteq B$, then $r(D)\le r(B).$

In practical problems, in order to reduce the complexity of fuzzy measure calculation, $\lambda$ fuzzy measure is usually used instead of general fuzzy measure.

Definition 2.6

(Choquet, 1954) For any $D,B\in P(X)$, $D \cap B=\emptyset$, if the fuzzy measure $r_{\lambda }$ satisfies $r(D\cup B)=r(D)+r(B)+\lambda r(D)r(B)$, where $\lambda \in (-1,\infty )$, then $r_{\lambda }$ is called as $\lambda -$ fuzzy measure.

Let X be a finite set, and $\bigcup ^{n}_{i=1}x_{i}=X$. The $\lambda -$ fuzzy measure r satisfies

$$\begin{aligned} r(X)=r(\bigcup ^{n}_{i=1}x_{i})={\left\{ \begin{array}{ll}\frac{1}{\lambda }(\Pi ^{n}_{i=1}[1+\lambda r(x_{i})]-1),\quad (if \lambda \ne 0) \\ \sum ^{n}_{i=1}r(x_{i}),\quad (if \lambda =0)\\ \end{array}\right. }, \end{aligned}$$

(8)

where $x_{i}\bigcap x_{j}=\emptyset$ for all $i,j=1,2,\ldots ,n$ and $i\ne j$. $r(x_{i})$ denotes a fuzzy density of $x_{i}$, simplified as $r_{i}=r(x_{i})$.

For every subset $D\in P(X)$, we have

$$\begin{aligned} r(D)={\left\{ \begin{array}{ll}\frac{1}{\lambda }(\Pi _{i\in D}[1+\lambda r(i)]-1),\quad (if \lambda \ne 0) \\ \sum _{i\in D}r(i),\quad (if \lambda =0)\\ \end{array}\right. }. \end{aligned}$$

(9)

When $r(X)=1$. which is equivalent to solving

$$\begin{aligned} \lambda +1=\Pi ^{n}_{i=1}(1+\lambda r_{i}), \end{aligned}$$

(10)

where $\lambda$ can be uniquely determined by $r(X)=1$.

Definition 2.7

(Choquet, 1954) Given that $X=\{x_{1},x_{2},\ldots ,x_{n}\}$ is a nonempty finite set, f is a nonnegative discrete function defined on X. Assume that $f(x_{1})\le f(x_{2}) \le \cdots \le f(x_{n})$, $\mu$ is a $\lambda -$ fuzzy measure on X. The Choquet fuzzy integral operator of the function f with respect to $\mu$ is defined as

$$\begin{aligned} CI_{\mu }(f)=(C)\int fd\mu =\Sigma ^{n}_{i=1}f(x_{i})[\mu (D_{i})-\mu (D_{i+1})], \end{aligned}$$

(11)

where $(C)\int fd\mu$ denotes Choquet fuzzy integral operator, $D_{i}=\{x_{i},x_{i+1},\ldots ,x_{n}\}$.

3 A novel DHHFL DTRS model based on prospect theory

As the introduction of DHHFLTSs (Gou et al., 2017), it consists of two hierarchy completely independent LTSs and improves the accuracy of linguistic expression. In this section, DHHFLTSs are used to describe the benefit and loss functions in TWDs. Then a novel DTRSs model is proposed with DHHFLT information. There are two states and three actions in the new DTRS model. $\Omega$ = $\{A,A^{c}\}$ represents the set of states which manifests that an element is in A or not in A. As for three actions, $\Lambda$ = $\{a_{P},a_{B},a_{N}\}$ denotes the set of actions, and they are used to classify an object $x_{i}$. $a_{P}$ represents $x_{i}\epsilon POS(A)$, $a_{B}$ represents $x_{i}\epsilon BND(A)$, and $a_{N}$ represents $x_{i}\epsilon NEG(A)$, where $POS(A),BND(A),NEG(A)$ denote the positive region, the boundary region and the negative region of A respectively. The states represent overall situation of the object and the actions represent our judgements. We construct the benefit and loss function matrixes under the DHHFLT environment. The results are displayed in Tables 1 and 2.

Table 1 The DHHFLT benefit function of the actions in different states

Table 2 The DHHFLT loss function of the actions in different states

From Tables 1 and 2, we can attain that the benefit and loss functions are DHHFLEs. $h^{b(\lambda )_{PP}}_{S_{o}}$, $h^{b(\lambda )_{BP}}_{S_{o}}$ and $h^{b(\lambda )_{NP}}_{S_{o}}$ represent the benefit (loss) degrees with DHHFLEs caused by taking actions of $a_{P}$, $a_{B}$ and $a_{N}$ to x given state A, respectively. Analogously, $h^{b(\lambda )_{PN}}_{S_{o}}$, $h^{b(\lambda )_{BN}}_{S_{o}}$ and $h^{b(\lambda )_{NN}}_{S_{o}}$ represent the benefit (loss) degrees caused by taking the same actions to x given state $A^{c}$. Thus, in this case, $h^{b(\lambda )_{\cdot \cdot }}_{S_{o}}\ne \emptyset$. Based on the property of DHHFLEs and the semantics of DTRS (Liang & Liu, 2015), we can attain a reasonable relationship as follows:

$$\begin{aligned} h^{b_{PP}}_{S_{o}}\succeq h^{b_{BP}}_{S_{o}}\succ h^{b_{NP}}_{S_{o}}, \end{aligned}$$

(12)

$$\begin{aligned} h^{b_{NN}}_{S_{o}}\succeq h^{b_{BN}}_{S_{o}}\succ h^{b_{PN}}_{S_{o}}. \end{aligned}$$

(13)

That is, the benefit degrees of right judgment are not less than the benefit degrees of delaying decision, and the benefit degrees of delaying decision are more than the benefit degrees of wrong judgment.

$$\begin{aligned} h^{\lambda _{PP}}_{S_{o}}\preceq h^{\lambda _{BP}}_{S_{o}}\prec h^{\lambda _{NP}}_{S_{o}}, \end{aligned}$$

(14)

$$\begin{aligned} h^{\lambda _{NN}}_{S_{o}}\preceq h^{\lambda _{BN}}_{S_{o}}\prec h^{\lambda _{PN}}_{S_{o}}. \end{aligned}$$

(15)

That is the loss degrees of wrong judgment are more than the loss degrees of delaying decision, and the loss degrees of delaying decision are not less than the loss degrees of correct judgment.

For any object $x_{i}$, when the decision maker takes the action $a_{\diamond }$, the comprehensive value $v_{\diamond \cdot }$ can be attained as follows:

$$\begin{aligned} v_{\diamond \cdot }= F(le(h^{b_{\diamond \cdot }}_{S_{o}}))- F(le(h^{\lambda _{\diamond \cdot }}_{S_{o}})). \end{aligned}$$

(16)

with $\diamond \in \{P,B,N\}$ and $\cdot \in \{P,N\}$. Then the utility value $u(v_{\diamond \cdot })$ of $v_{\diamond \cdot }$ can be calculated by

$$\begin{aligned} u(v_{\diamond \cdot })={\left\{ \begin{array}{ll}(v_{\diamond \cdot })^{\alpha },\quad (v_{\diamond \cdot })\ge 0) \\ -\theta (-v_{\diamond \cdot })^{\beta },\quad (v_{\diamond \cdot })<0)\\ \end{array}\right. }, \end{aligned}$$

(17)

where $\diamond \in \{P,B,N\}$ and $\cdot \in \{P,N\}$.

Based on the Bayesian decision procedure of reference Yao et al. (1990), the conditional probability is one of the important elements. $Pr(X|x_{i})$ is the conditional probability of an object $x_{i}$ belonging to A, and $Pr(A^{c}|x_{i})$ is the conditional probability of the object belonging to $A^{c}$. they are all real numbers, and they satisfy: $Pr(A|x_{i})+Pr(A^{c}|x_{i})=1$. Then, given an object $x_{i}$, we can calculate the expected utility $U(a_{\diamond }|x_{i}) (\diamond =P,B,N)$ under the corresponding actions as follows:

$$\begin{aligned} U(a_{P}|x_{i})=u(v_{PP})Pr(A|x_{i})+u(v_{PN})Pr(A^{c}|x_{i}); \end{aligned}$$

(18)

$$\begin{aligned} U(a_{B}|x_{i})=u(v_{BP})Pr(A|x_{i})+u(v_{BN})Pr(A^{c}|x_{i}); \end{aligned}$$

(19)

$$\begin{aligned} U(a_{N}|x_{i})=u(v_{NP})Pr(A|x_{i})+u(v_{NN})Pr(A^{c}|x_{i}). \end{aligned}$$

(20)

On the basis of the results given in references Yao et al. (1990) and Yao (2010), the maximum-utility decision rules can be deduced as follows:

(P) If $U(a_{P}|x_{i})\ge U(a_{B}|x_{i})$ and $U(a_{P}|x_{i})\ge U(a_{N}|x_{i})$, decide $x_{i}\in$ POS(A);

(B) If $U(a_{B}|x_{i})\ge U(a_{P}|x_{i})$ and $U(a_{B}|x_{i})\ge U(a_{N}|x_{i})$, decide $x_{i}\in$ BND(A); and

(N) If $U(a_{N}|x_{i})\ge U(a_{P}|x_{i})$ and $U(a_{N}|x_{i})\ge U(a_{B}|x_{i})$, decide $x_{i}\in$ NEG(A).

The positive rule(P) implies taking the action of acceptance, i.e., $x_{i}\in POS(A)$. The boundary rule (B) implies taking the action of delaying the decision, i.e., $x_{i}\in BND(A)$. And the negative rule (N) implies taking the action of rejection, i.e., $x_{i}\in NEG(A)$.

In light of the decision-making rules (Yao et al., 1990) in DTRS model, we substitute the expression (18)–(20) of expected utility $U(a_{\diamond }|x_{i}) (\diamond =P,B,N)$ into the decision rule$(P)-(N)$, and transform the inequality into the form of conditional probability and threshold comparison by deformation. The decision-making rules in the new model can be deduced as follows:

($P_{1}$) If $Pr(A|x_{i})\ge \alpha$ and $Pr(A|x_{i}) \ge \gamma$, decide $x_{i} \in$ POS(A);

($B_{1}$) If $Pr(A|x_{i}) \le \alpha$ and $Pr(A|x_{i}) \ge \beta$, decide $x_{i} \in$ BND(A); and

($N_{1}$) If $Pr(A|x_{i}) \le \beta$ and $Pr(A|x_{i}) \le \gamma$, decide $x_{i} \in$ NEG(A).

Among them, the thresholds $\alpha ,\beta ,\gamma$ are calculated by the utility functions $u(v_{\diamond \cdot })$ as follows:

$$\begin{aligned} \alpha =\frac{u(v_{BN})-u(v_{PN})}{u(v_{BN})-u(v_{PN})+u(v_{PP})-u(v_{BP})}; \end{aligned}$$

(21)

$$\begin{aligned} \beta =\frac{u(v_{NN})-u(v_{BN})}{u(v_{NN})-u(v_{BN})+u(v_{BP})-u(v_{NP})}; \end{aligned}$$

(22)

$$\begin{aligned} \gamma =\frac{u(v_{NN})-u(v_{PN})}{u(v_{NN})-u(v_{PN})+u(v_{PP})-u(v_{NP})}. \end{aligned}$$

(23)

Actually, the decision rules $(P_{1})-(N_{1})$ are equivalent to the decision rules$(P)-(N)$. $P_{1}:$ Given an object $x_{i}$, when the conditional probability of the state A occurrence is not less than the thresholds $\alpha$ and $\gamma$, then the object $x_{i}$ is classified into the positive region POS(A). It means that investors should invest in this project; $B_{1}:$ Given an object $x_{i}$, when the conditional probability of the state A occurrence lies within the interval formed by the two thresholds $\beta$ and $\alpha$, then the object $x_{i}$ is classified into the boundary region BND(A). It means that investors should gather more information before making a decision; $N_{1}:$ Given an object $x_{i}$, when the conditional probability of the state A occurrence does not exceed the thresholds $\beta$ and $\gamma$, then the object $x_{i}$ is classified into the negative region NEG(A). It means that investors should reject the project.

4 Calculation of conditional probability with Choquet-based bi-projection method

From the decision-making rules $P_{1}-N_{1}$, we can learn that there are two important ingredients in the TWDs: the calculation of threshold and conditional probability. In Sect. 3, we have constructed a novel DTRS model with DHHFLT expression of benefit and loss functions. As for the calculation of the conditional probability, it depends on DHHFLT information systems. Therefore, we need to define the DHHFLT information systems firstly. Let $AT=\{c_{1},c_{2},\ldots ,c_{n}\}$ be a conditional attribute set of the DHHFLT information systems. $V=\bigcup _{a\in AT}V_{a}$, $V_{a}$ denotes a domain of the attribute a. $g:U\times AT\rightarrow V$ denotes a function, such that $g(x_{i},a)\in V_{a}$ for every $a\in AT, x_{i}\in U$, where $g(x_{i},a)$ denotes a DHHFLT. $U=\{x_{1},x_{2},\ldots ,x_{m}\}$ is a discrete set of m feasible objects. The evaluation of the object $x_{i}$ regarding the attribute $a_{j}$ is expressed by $g(x_{i},a_{j})=h^{ij}_{S_{o}}(i=1,2,\ldots ,m;j=1,2,\ldots ,n)$.

For example, a customer wants to buy one of four cars $x_{1}-x_{4}$, four attributes are shown as follows: (1) $c_{1}$ price level; (2) $c_{2}$ comfort level; (3) $c_{3}$ safety level; (4) $c_{4}$ velocity level, where $c_{1}$ belongs to cost attribute, the others belong to benefit attributes. In order to eliminate the influence of different attribute types, the decision matrix should be normalized, the cost attribute should be transformed into the benefit attribute, and the decision matrix $D=(h_{ij})_{m\times n}$ should be normalized as $Q=(q_{ij})_{m\times n},i=1,2,\ldots ,m, j=1,2,\ldots ,n,$. The specific transformation formula is shown as follows:

$$\begin{aligned} q_{ij}={\left\{ \begin{array}{ll} h_{ij},\quad (if\, c_{j}\, is\, benefit\, attribute) \\ 1-h_{ij},\quad (if\, c_{j}\, is\, cost\, attribute)\\ \end{array}\right. }. \end{aligned}$$

(24)

Next, we need to determine the positive and negative ideal solutions of the DHHFLT information system.

Definition 4.1

(Liu et al., 2014) Given that $Q=(q_{ij})_{m\times n}$ is normalized decision matrix,

$$\begin{aligned} X^{+}=(q_{1}^{+},q_{2}^{+},\ldots ,q_{n}^{+}),X^{-}=(q_{1}^{-},q_{2}^{-},\ldots ,q_{n}^{-}). \end{aligned}$$

(25)

is the vector formed by positive ideal solution (PIS) and negative ideal solution (NIS) respectively, where $q_{j}^{+}=\max \limits _{1\le i\le m}\{q_{ij}\}$, $q_{j}^{-}=\min \limits _{1\le i\le m}\{q_{ij}\}$,$j=1,2,\ldots ,n.$ Where $q_{ij}$ is not limited to the evaluation of existing projects, but also includes the evaluation of ideal projects. Combining the TWDs, the PIS and the NIS correspond to the set of states, i.e., A and $A^{c}$.

When attributes are interrelated of each other, Choquet integral (Choquet, 1954) is an appropriate tool to attain the weights of attributes. Based on the formulas (8)–(11), the weights of attributes can be calculated by

$$\begin{aligned} \omega _{j}=r(D_{j})-r(D_{j+1}), \end{aligned}$$

(26)

where $D_{i}=\{c_{i},c_{i+1},\ldots ,c_{n}\}$.

Then we need to calculate the conditional probability with Choquet-based bi-projection method. Each scheme is taken as a vector in the bi-projection model, which is convenient to evaluate the information in terms of the direction and the length.

Definition 4.2

Given that $\omega =(\omega _{1},\omega _{2},\ldots ,\omega _{n})$ is the weight vector of attributes. Then the weighted projection of the vector formed by the i th scheme and the NIS on the vector formed by the PIS and NIS, and the weighted projection of the vector formed by the PIS and NIS on the scheme and the PIS can be calculated by

$$\begin{aligned} Prj_{X^{-}X^{+}}(X^{-}X_{i})_{\omega }=|X^{-}X_{i}|_{\omega }\cos (X^{-}X_{i}, X^{-}X^{+})_{\omega }=\frac{\sum ^{n}_{j=1}d_{ij}(q^{+}_{j},q^{-}_{j})_{\omega }d_ {ij}(q_{ij},q^{-}_{j})_{\omega }}{|X^{-}X^{+}|_{\omega }}, \end{aligned}$$

(27)

$$\begin{aligned} Prj_{X_{i}X^{+}}(X^{-}X^{+})_{\omega }=|X^{-}X^{+}|_{\omega }\cos (X^{-}X^{+},X_{i}X^ {+})_{\omega }=\frac{\sum ^{n}_{j=1}d_{ij}(q^{+}_{j},q^{-}_{j})_{\omega }d_{ij}(q^{+}_ {j},q_{ij})_{\omega }}{|X_{i}X^{+}|_{\omega }}. \end{aligned}$$

(28)

where $X^{+}$ denotes PIS, that is the best solution you can imagine. $X^{-}$ denotes NIS, that is the worst solution you can imagine. And the weighted modulus-length of two vectors of schemes is calculated as follows:

$$\begin{aligned} |X^{-}X^{+}|_{\omega }=\sqrt{\sum ^{n}_{j=1}(d_{ij}(q^{+}_{j},q^{-}_{j})_{\omega })^{2}}, \end{aligned}$$

(29)

$$\begin{aligned} |X^{-}X_{i}|_{\omega }=\sqrt{\sum ^{n}_{j=1}(d_{ij}(q_{ij},q^{-}_{j})_{\omega })^{2}}. \end{aligned}$$

(30)

The weighted cosine of the angle between the two scheme vectors is calculated by

$$\begin{aligned} \cos (X^{-}X_{i},X^{-}X^{+})_{\omega }=\frac{\sum ^{n}_{j=1}d_{ij}(q^{+}_{j},q^{-}_{j})_ {\omega }d_{ij}(q_{ij},q^{-}_{j})_{\omega }}{|X^{-}X_{i}|_{\omega }|X^{-}X^{+}|_{\omega }}, \end{aligned}$$

(31)

$$\begin{aligned} \cos (X^{-}X^{+},X_{i}X^{+})_{\omega }=\frac{\sum ^{n}_{j=1}d_{ij}(q^{+}_{j},q^{-}_{j})_ {\omega }d_{ij}(q^{+}_{j},q_{ij})_{\omega }}{|X_{i}X^{+}|_{\omega }|X^{-}X^{+}|_{\omega }}. \end{aligned}$$

(32)

the weighted cosine reflects the consistency of the two scheme vectors in direction, where the distance measure of the scheme i with respect to the attribute j is calculated as follows: $d_{ij}(q^{+}_{j},q^{-}_{j})=|q^{+}_{j}-q^{-}_{j}|,d_{ij}(q^{+}_{j},q_{ij})=|q^{+}_ {j}-q_{ij}|,d_{ij}(q_{ij},q^{-}_{j})=|q_{ij}-q^{-}_{j}|$. In the process of weighted aggregation, the distance measures need to be ranked, so that $d_{i(1)}(q^{+}_{j},q^{-}_{j})\le d_{i(2)}(q^{+}_{j},q^{-}_{j})\le \cdots \le d_{i(n)}(q^{+}_{j},q^{-}_{j})$, $d_{i(1)}(q^{+}_{j},q_{ij})\le d_{i(2)}(q^{+}_{j},q_{ij})\le \cdots \le d_{i(n)}(q^{+}_{j},q_{ij})$ and $d_{i(1)}(q_{ij},q^{-}_{j})\le d_{i(2)}(q_{ij},q^{-}_{j})\le \cdots \le d_{i(n)}(q_{ij},q^{-}_{j})$. Then the weighted distance measure of the scheme i with respect to the attribute j can be calculated as follows:

$$\begin{aligned} d_{ij}(q^{+}_{j},q^{-}_{j})_{\omega }=d_{i(j)}(q^{+}_{j},q^{-}_{j})\omega _{j}, \end{aligned}$$

(33)

$$\begin{aligned} d_{ij}(q^{+}_{j},q_{ij})_{\omega }=d_{i(j)}(q^{+}_{j},q_{ij})\omega _{j}, \end{aligned}$$

(34)

$$\begin{aligned} d_{ij}(q_{ij},q^{-}_{j})_{\omega }=d_{i(j)}(q_{ij},q^{-}_{j})\omega _{j}. \end{aligned}$$

(35)

Then the closeness degree is considered as the conditional probability that the object belongs to the state A.

$$\begin{aligned} Pr(A|x_{i})=C(x_{i})_{\omega }=\frac{Prj_{X^{-}X^{+}}(X^{-}X_{i})_{\omega }}{Prj_{X^{-}X^{+}}(X^{-}X_{i})_{\omega }+Prj_{X_{i}X^{+}}(X^{-}X^{+})_{\omega }}, \end{aligned}$$

(36)

where $0\le Pr(A|x_{i})\le 1$, $C(x_{i})_{\omega }$ denotes the weighted closeness degree of the project $x_{i}$.

5 The process of three-way decisions

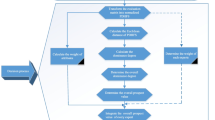
By introducing the results mentioned above, we proposed a novel method of TWDs in the DHHFLT environment. The specific steps of the proposed method are shown as follows.

Step 1: Based on the practical context, we determine the elements of DHHFLT information system $IS=(U,AT,V,g)$, including objects and attributes. Then, we collect the outcomes of IS, and we construct the benefit and loss function matrixes of Tables 1 and 2 accordingly.

Step 2: According to the formulas (2) and (6), the evaluation value with DHHFLT is transformed to a real number. Then, we can obtain normalized information matrix $H_{k}=[h^{k}_{ij}]_{m\times n}$, where $h_{ij}=F(le(h^{ij}_{S_{o}}))$.

Step 3: We check the conditional attributes of IS, if all the attributes belong to profit attribute, go to Step 5. Otherwise, move on to the next step.

Step 4: To keep the types of attributes consistent, we need to convert the cost attribute to the profit attribute. The decision matrix $H_{k}=(h^{k}_{ij})_{m\times n}$ should be normalized as $Q_{k}=(q^{k}_{ij})_{m\times n}, k=1,2,\ldots ,l, i=1,2,\ldots ,m, j=1,2,\ldots ,n,$ based on the formula (24).

Step 5: Determine PIS $X^{+}$ and NIS $X^{-}$ based on the formula (25). Combining the TWDs, the PIS and the NIS correspond to the set of states, i.e., A and $A^{c}$.

Step 6: Confirm the fuzzy density $r_{j}=r(c_{j})$ of each attribute. Then the parameter $\lambda$ of attributes can be calculated by the formula (10) and the weights of attributes can be calculated by the formula (26). The purpose of this step is determining the weights of the attribute by the Choquet integral method.

Step 7: The conditional probability can be calculated by the formula (36). Then we can get the conditional probability that the object belongs to the state A based on the bi-projection method.

Step 8: Based on the loss and benefit functions matrixes, the thresholds $\alpha ,\beta ,\gamma$ can be calculated respectively by the formulas (21)–(23).

Step 9: In the light of the decision rules $P_{1}-N_{1}$, we can ascertain the decision result for each object further. And the decision rules $P_{1}-N_{1}$ are deduced by the maximum-utility principle.

For the sake of clarity, the decision-making process of our proposed model is shown in Fig. 1.

Fig. 1

The decision-making process of our proposed model

6 A case study about the selection of investment projects during the epidemic

In 2020, we witnessed the tremendous impact of COVID-19. The economy of China went from a shutdown to a gradual recovery. The investment market also experienced ups and downs, and rebounded after two big falls. Facing the turbulence in the investment market, many enterprises find it difficult to judge the development prospects of investment projects and make the right investment decisions. Then, we analyze the investment projects with our proposed TWDs model. Here are seven investment projects that enterprise need to make investment choices. They are $U=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6},x_{7}\}$. Among them, $x_{1}$ and $x_{5}$ belong to the biomedical industry sector, $x_{2}$ and $x_{7}$ belong to the building materials industry sector, $x_{3}$ and $x_{6}$ belong to the food and beverage industry sector, $x_{4}$ belongs to the technology industry sector. Before making decisions, the enterprise need to assess the probability that the investment project will make a profit. Thus, in the frame of TWDs, the set of the states $\Omega$ = $\{A, A^{c}\}$ indicates that these investment projects are profitable or unprofitable. We calculate the conditional probability based on DHHFLT information systems, and determine the conditional attribute in the information system as: $c_{1}$: The severity of epidemic situation. Experts believe that the biggest external driver of the investment market in the first half of the year is the development of COVID-19 and the expectation of the development of the epidemic; $c_{2}$: Policies environment. They include fiscal and monetary policies. And they are affected to some extent by the development of the epidemic; $c_{3}$: Industry development prospect. During the epidemic, investment projects in different sectors were affected by the epidemic to varying degrees. For example, in the period of accelerated spread of the epidemic in China, the offline consumption and service industries that are most seriously affected by the epidemic are relatively depressed, while the epidemic concept investment project, such as medicine and biology, and some industries that are less affected by the epidemic are relatively resilient; $c_{4}$: Innovation. Innovation is an important criterion to judge whether an investment project has development prospect. It reflects whether a project has investment value. Based on the development of the epidemic in the first half of the year and the major changes in the trend of the Chinese investment market, we divide the performance of the Chinese investment market into four stages: $T_{1}$: The stage of downturn led by domestic epidemic. $T_{2}$: The stage of rapid rebound. $T_{3}$: The stage of decline dominated by epidemic overseas. $T_{4}$: The stage of rising. In this section, we apply the method of Sect. 5 to conduct investment projects’ valuation and make decisions for the enterprise.

Step 1: We need to identify the basic elements of DHHFLT information system $IS=(U,AT,V,g)$. Then we can obtain: $U=\{x_{1},x_{2},\ldots ,x_{7}\}$ and $AT=\{c_{1},c_{2},c_{3},c_{4}\}$. And all the evaluation will be provided based on the following two LTSs by the experts:

$$\begin{aligned} \begin{aligned}&S=\{s_{-4}=\mathrm extremely\, low, s_{-3}=vely\, low, s_{-2}=low, s_{-1}=slightly\, low, s_{0}=medium,\\&\mathrm s_{1}=slightly\, high, s_{2}=high, s_{3}=very\, high, s_{4}=extremely\, high\} \end{aligned} \\ \begin{aligned}&O=\{o_{-4}=\mathrm far\, from, o_{-3}=scarcely, o_{-2}=only\, a\, little, o_{-1}=a\, little, o_{0}=just\, right,\\&\mathrm o_{1}=much, o_{2}=very\, much, o_{3}=extremely\, much, o_{4}=entirely\} \end{aligned} \end{aligned}$$

Then, we collect evaluation for each investment project regarding the attributes $c_{1}-c_{4}$ from the experts in enterprise. Experts evaluate attributes based on their knowledge and historical experience. Then they use DHHFLT to describe their evaluation information. The corresponding DHHFLT information systems for four stages are displayed in Tables 3, 4, 5 and 6.

Table 3 The corresponding DHHFLT information system during the stage of $T_{1}$

Table 4 The corresponding DHHFLT information system during the stage of $T_{2}$

Table 5 The corresponding DHHFLT information system during the stage of $T_{3}$

Table 6 The corresponding DHHFLT information system during the stage of $T_{4}$

For each element of Tables 3, 4, 5 and 6, it is expressed by a DHHFLT. And it represents the evaluation of the object $x_{i}$ regarding the attribute $c_{j} (i=1,2,\ldots ,7; j=1,2,\ldots ,4)$. During the same stage, all investment projects are evaluated the same on attributes $c_{1}$ and $c_{2}$. Based on the industry sector, these investment projects are divided into four categories: the biomedical industry sector, the building materials industry sector, the food and beverage industry sector and the technology industry sector. The investment projects which belong to the same industry sector will be given the same estimation about the attribute $c_{3}$. Then we construct the benefit function matrix and the loss function matrix for taking different actions in a state as Tables 7 and 8.

Table 7 Benefit function information with DHHFLT

Table 8 Loss function information with DHHFLT

All the information about the benefit and loss functions comes from assessments by the experts in enterprise.

Step 2: According to the formulas (2) and (6), the evaluation value of Table 3 is transformed to a real number. Then, we can obtain a normalized information matrix in Table 9.

Table 9 The normalized information matrix during the stage of $T_{1}$

Steps 3–4: We check the conditional attributes of IS, the attribute $c_{1}$ belongs to cost attribute, the attributes $c_{2},c_{3},c_{4}$ belong to benefit attribute. We convert the cost attribute to the benefit attribute based on the formula (21). The result of the conversion is shown in Table 10.

Table 10 The attributes converted information matrix during the stage of $T_{1}$

Steps 5-6: Based on the formula (25), the PIS and NIS can be determined as: $X^{+}=(1,1,1,1),X^{-}=(0,0,0,0)$. Then we determine fuzzy density of each criterion, and its $\lambda$ parameter. Suppose $r(c_{1})=0.40,r(c_{2})=0.2,r(c_{3})=0.37,r(c_{4})=0.25$ (Tan, 2011). On the basic of Eq. (10), the $\lambda$ of the criteria can be determined: $\lambda =-0.44$. By Eq. (10), we have $r(c_{1},c_{2})=0.56,r(c_{1},c_{3})=0.70,r(c_{1},c_{4})=0.60,r(c_{2},c_{3})=0.54 ,r(c_{2},c_{4})=0.43,r(c_{3},c_{4})=0.68,r(c_{1}, c_{2},c_{3})=0.84,r(c_{1},c_{2},c_{4})=0.75, r(c_{1},c_{3},c_{4})=0.88,r(c_{2},c_{3},c_{4})=0.73,r(c_{1},c_{2},c_{3},c_{4})=1$. Then the weight of attributes can be calculated by Eq. (26), $\omega _{1}=r(D_{1})-r(D_{2})=1-0.73=0.27,\omega _{2}=r(D_{2})-r(D_{3})=0.73-0.68=0. 05,\omega _{3}=r(D_{3})-r(D_{4})=0.68-0.25=0.43,\omega _{4}=r(D_{4})=0.25$. where $D_{i}=\{c_{i},c_{i+1},\ldots ,c_{n}\}$.

Step 7: The conditional probabilities of these investment projects will make a profit are calculated by the formula (36). The results are displayed in Table 11.

Table 11 The weighted projection distances and conditional probabilities during the stage of $T_{1}$

Step 8: Assumed that $\rho =\delta =0.88$ and $\theta =2.25$, which is consistent with the empirical evidence afterwards (Tversky & Kahneman, 1992). In light of the loss functions matrixes, the thresholds $\alpha ,\beta ,\gamma$ can be calculated respectively by the formulas (21)–(23). The results of calculation are shown in Tables 12 and 13.

Table 12 The values for taking different actions in a state

Table 13 The results of thresholds

Because there is a relationship between the threshold we obtained: $\alpha>\gamma >\beta$, we just need to concern about the values of $\alpha$ and $\beta$.

Step 9: According to the decision rules $P_{1}-N_{1}$, we can ascertain the decision result for each object. The results are shown in Fig. 2 and Table 14. During the stage $T_{1}$, $POS(A)=\{x_{1},x_{4}\}$; $BND(A)=\{x_{2},x_{3},x_{5},x_{6},x_{7}\}$. Due to the outbreak of COVID-19 in China, epidemic has become an important factor dominating the domestic investment market. In the short term, monetary policy has not been adjusted and liquidity has not improved. Industries affected by the outbreak include building materials, food and beverages. But the medical and biological industry that benefits from the epidemic is relatively resilient. $x_{1}$ is a investment project in the medical and biological industry with high-level innovation, which can be held and bought as an investment. As a high-tech investment project, $x_{4}$ is also a good choice. During the stage $T_{2}$, $POS(A)=\{x_{1},x_{2},x_{4},x_{5}\}$, $BND(A)=\{x_{3},x_{6},x_{7}\}$. the epidemic in China has gradually moved from an outbreak phase to a remission phase. The overall liquidity of the market is relatively comfortable, market interest rates continue to decline. In the market performance, technology sector strongly rebounds. During the stage $T_{3}$, $POS(A)=\{x_{1},x_{3},x_{4},x_{6}\}$, $BND(A)=\{x_{2},x_{5},x_{7}\}$. In China, the epidemic eased and work resumed in an orderly manner. The spread of the epidemic overseas has become the core contradiction of the market. Industries with a high dependence on overseas demand have been affected. During the stage $T_{4}$, $POS(A)=\{x_{1},x_{2},x_{3},x_{4},x_{6}\}$, $BND(A)=\{x_{5},x_{7}\}$. Domestic transmission of the epidemic has been basically interrupted, while the epidemic in foreign countries has rebounded since it reached a plateau. Monetary policy is flexible and appropriate, liquidity margin is tightened. Fiscal policy will continue to strongly support the development of the real economy. The overall valuation of the Chinese investment market has been significantly repaired, benefiting from a gradual improvement in earnings and higher risk appetite. Then, $x_{1},x_{2},x_{3},x_{4},x_{6}$ can all be used as investment options, $x_{5},x_{7}$ need to gather more information and wait for further decisions.

Table 14 The conditional probabilities of investment projects making a profit during four stages

Fig. 2

The results of TWDs during four stages

7 Sensitivity analysis

In this section, the impact of using different values of the loss aversion factor $\theta$ is shown by a sensitivity analysis. Each investor’s risk attitude is different, so the sensitivity analysis of risk aversion factors is still necessary. The investor can determine the decision result correspondingly by changing the value of $\theta$. Then we calculate the thresholds parameters and deduce the decision result by taking $\theta =1.5,2,2.5,3$. The calculation results with different loss aversion factors are shown in Table 15.

Table 15 The thresholds parameters with different loss aversion factors

We can learn from Fig. 3 that the threshold parameter $\alpha$ increases when the loss aversion factor $\theta$ increases, the threshold parameter $\beta$ decreases when the loss aversion factor $\theta$ increases. It means that the boundary region will be expanded. That is, when investors tend to be risk-averse, they will increase the choice to delay decisions. During the stage $T_{1}$, when $\theta =1.5,POS(A)=\{x_{1},x_{4}\}$, $BND(A)=\{x_{2},x_{3},x_{5},x_{6}\}$,$NEG(A)=\{x_{7}\}$; when $\theta =2,POS(A)=\{x_{1},x_{4}\}$, $BND(A)=\{x_{2},x_{3},x_{5},x_{6},x_{7}\}$; when $\theta =2.5,POS(A)=\{x_{1}\}$, $BND(A)=\{x_{2},x_{3},x_{4},x_{5},x_{6},x_{7}\}$; when $\theta =3,POS(A)=\{x_{1}\}$, $BND(A)= \{x_{2},x_{3},x_{4},x_{5},x_{6},x_{7}\}$. From the decision result, we can learn that the number of elements in the positive region POS(A) decreases when the loss aversion factor $\theta$ increases, and the number of elements in the boundary region BND(A) increases when the loss aversion factor $\theta$ increases, the number of elements in the negative region NEG(A) decreases when the loss aversion factor $\theta$ increases. Therefore, we can learn that the risk aversion factor considering the decision maker’s boundary rationality is important in our proposed model.

Fig. 3

Sensitivity analysis of risk aversion factors

8 Comparison and discussion

Next, we will compare our proposed model with the other models and discuss the advantages and limitations of our proposed model. It is worth noting that the following TWDs problems are studied for the stage of $T_{1}$.

8.1 Three-way decisions model based on weighted aggregation

The TWDs model proposed by Ye et al. (2020) can deal with the information of fuzzy set. In order to facilitate comparison, we used Table 10 as the initial base information system. Ye et al. (2020) determined the weights of attributes by entropy weight method (Zhang & Zhou, 2008). Based on the formula $p_{ij}=\frac{q_{ij}}{\sum ^{m}_{i=1}q_{ij}}$, we transform the Table 10 into Table 16.

Table 16 The normalized information system

Then according to the formula $e_{j}=-\frac{1}{\ln n}\sum ^{m}_{i=1}p_{ij}\ln p_{ij}$, we can obtain: $e_{1}=1,e_{2}=1,e_{3}=0.892,e_{4}=0.965$. The entropy weight can be computed by the formula $\omega _{j}=\frac{1-e_{j}}{\sum ^{n}_{j=1}(1-e_{j})}$. Thus, we can attain a weight vector $W=(0,0,0.755,0.245)$.

Assume that $\sigma =(0.35,0.4,0.3,0.15)$, then we can calculate the probability by means of thought of weighted aggregation. Based on $Pr(A|x_{i})=\sum ^{n}_{j=1}q_{ij}\omega _{j}$, the conditional probability can be obtain in Table 17.

Table 17 The results of conditional probability

The thresholds $\alpha _{i},\beta _{i},\gamma _{i}$ to each alternative are calculated in Table 18.

Table 18 The results of threshold parameters

Then we can deduce the decision result: $POS(A)=\{x_{1},x_{4},x_{5}\},BND(A)=\{x_{3},x_{6}\},NEG(A)=\{x_{2},x_{7}\}$.

8.2 Three-way decisions based on the TOPSIS method

The TWDs model proposed by Liang et al. (2018) calculate the conditional probability by the TOPSIS method (Zhang & Xu, 2014). Based on the maximizing deviation method (Wang, 1997), we can determine the weights of attributes from Table 10. Then we can attain a weight vector $W=(0,0,0.574,0.426)$. The PIS and NIS are determined as $X^{+}=\{0.135,0.625,0.906,0.922\},X^{-}=\{0.135,0.625,0.188,0.281\}$. Then the conditional probability can be obtain in Table 19.

Table 19 The results of conditional probability

Based on the Table 12, the expected loss can be calculated in Table 20.

Table 20 The results of expected loss

According to minimum-cost decision rules, the decision result can be obtained: $POS(A)=\{x_{1},x_{4},x_{5}\},NEG(A)=\{x_{2},x_{3},x_{6},x_{7}\}$.

From Table 21, we can learn that the other results of our decisions are almost the same. And the differences are that, according to our results, the object $x_{5}$ is classified into BND(A) from POS(A), and the object $x_{2}$ is classified into BND(A) from NEG(A). The reasons can be concluded as follows.

Table 21 The comparison of decision results

(1) Due to that the object has the same evaluation value on attributes $c_{1}$ and $c_{2}$, information loss will be caused to some extent in the process of determining attribute weight by the entropy weight method (Zhang & Zhou, 2008) and the maximum deviation method (Wang, 1997). For instance, $\omega _{1}=0, \omega _{2}=0$ can be obtained based on their methods. Thus, the application of Choquet integral method, in this situation, avoids the loss of information which makes decision results more reasonable.

(2) Due to that the our proposed TWD model takes into account the bounded rationality of decision makers, and makes a decision by maximum-utility principle. However, the other methods make a decision by traditional minimum-loss principle.

8.3 Discussions on the advantages and limitations

The DTRSs model, as one of the elements of the TWDs, is mainly responsible for displaying the loss caused by the actions taken by the object in different states, and selecting the action with the minimum loss. The conditional probability is the other elements of the TWDs method. In the most of the existing TWDs models (Liang et al., 2013, 2017), the conditional probability is given directly which makes the decision result seem not so rigorous. We get the weight of each attribute by Choquet integral method, and take the closeness degree of objects calculated by the bi-projection method as the conditional probability. According to the profit purpose of investors, we take maximum-utility as the decision-making principle.

In the description of the qualitative problem, the linguistic terms conform with peoples habits of expression more. Differ from single linguistic term set, DHHFLTSs provide more flexible manner to express qualitative information. Our proposed model is constructed under the DHHFLT environment. DHHFLT was mostly applied in the multi-attribute decision making methods (Gou et al., 2017, 2018) previously, the TWDs models based on the DHHFLT information systems is a new research content. It has high research value.

The main advantages of the proposed method are displayed as follows.

• (1) We apply the TWDs model to the selection of investment projects during the epidemic. The model meets the decision-making needs of enterprises. According to the profit purpose of enterprises, we take maximum utility as the decision-making principle. And based on different risk attitudes of investors, we introduce prospect theory into the processing of benefit and loss function.

• (2) Considering the interplay of project’s attributes, the weight of attributes is determined by Choquet integral method, and the conditional probability is calculated by the bidirectional projective method which makes the decision results more objective and reliable.

However, there are some limitations with the proposed model.

• (1) For convenience of calculations, this paper does not discuss the situation of group decisions, nor does it take into account the weights of different experts. We plan to extend this model to group decisions in future work, and make it more practical.

9 Conclusions

In this paper, the TWDs with DTRSs are extended to the DHHFLT environment by considering the benefit and loss functions being expressed by DHHFLTs. Considering the interplay of project attributes, the weights of attributes are determined with the Choquet integral method. And the closeness degree calculated by Choquet-based bi-projection method is taken as the conditional probability, which makes decisions more rational. Next, the specific steps of the proposed model are designed. Finally, the TWD model is applied to the selection of investment projects during the epidemic. This research provides a scientific decision-making method for all enterprises to choose the suitable investment projects during the period of epidemic from the perspective of TWDs, so as to maximize the utility. Therefore, the proposed model has relatively high value in theory and application. And we will apply this model to more fields in the future.