Skip to main content
SpringerLink
Log in

Nonconvex Optimization for Robust Tensor Completion from Grossly Sparse Observations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

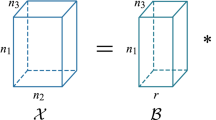
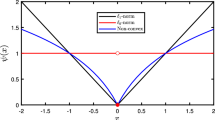
In this paper, we consider the robust tensor completion problem for recovering a low-rank tensor from limited samples and sparsely corrupted observations, especially by impulse noise. A convex relaxation of this problem is to minimize a weighted combination of tubal nuclear norm and the \(\ell _1\)-norm data fidelity term. However, the \(\ell _1\)-norm may yield biased estimators and fail to achieve the best estimation performance. To overcome this disadvantage, we propose and develop a nonconvex model, which minimizes a weighted combination of tubal nuclear norm, the \(\ell _1\)-norm data fidelity term, and a concave smooth correction term. Further, we present a Gauss–Seidel difference of convex functions algorithm (GS-DCA) to solve the resulting optimization model by using a linearization technique. We prove that the iteration sequence generated by GS-DCA converges to the critical point of the proposed model. Furthermore, we propose an extrapolation technique of GS-DCA to improve the performance of the GS-DCA. Numerical experiments for color images, hyperspectral images, magnetic resonance imaging images and videos demonstrate that the effectiveness of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. http://sipi.usc.edu/database/.

  2. https://engineering.purdue.edu/~biehl/MultiSpec/hyperspectral.html.

  3. http://media.xiph.org/video/derf/.

References

  1. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137(1–2), 91–129 (2013)

    Article  MathSciNet  Google Scholar 

  2. Ahn, M.J., Pang, J.S., Xin, J.: Difference-of-convex learning: directional stationarity, optimality, and sparsity. SIAM J. Optim. 27(3), 1637–1665 (2017)

    Article  MathSciNet  Google Scholar 

  3. Bai, M.R., Zhang, X.J., Ni, G.Y., Cui, C.F.: An adaptive correction approach for tensor completion. SIAM J. Imaging Sci. 9(3), 1298–1323 (2016)

    Article  MathSciNet  Google Scholar 

  4. Bai, M.R., Zhang, X.J., Shao, Q.Q.: Adaptive correction procedure for TVL1 image deblurring under impulse noise. Inverse Probl. 32, 085004 (2016)

    Article  MathSciNet  Google Scholar 

  5. Bochnak, J., Coste, M., Roy, M.F.: Real Algebraic Geometry. Ergeb. Math. Grenzgeb 36. Springer, Berlin (1998)

    Book  Google Scholar 

  6. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1), 459–494 (2014)

    Article  MathSciNet  Google Scholar 

  7. Candès, E.J., Ma, Y., Wright, J., Li, X.: Robust principal component analysis? J. ACM 58, 1–37 (2011)

    Article  MathSciNet  Google Scholar 

  8. Fan, H.Y., Chen, Y.J., Guo, Y.L., Zhang, H.Y., Kuang, G.Y.: Hyperspectral image restoration using low-rank tensor recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 10, 4589–4604 (2017)

    Article  Google Scholar 

  9. Fan, J.Q., Li, R.Z.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96(456), 1348–1360 (2001)

    Article  MathSciNet  Google Scholar 

  10. Gandy, S., Recht, B., Yamada, I.: Tensor completion and low-n-rank tensor recovery via convex optimization. Inverse Probl. 27(2), 025010 (2011)

    Article  MathSciNet  Google Scholar 

  11. Goldfarb, D., Qin, Z.W.: Robust low-rank tensor recovery: models and algorithms. SIAM J. Matrix Anal. Appl. 35(1), 225–253 (2014)

    Article  MathSciNet  Google Scholar 

  12. Gu, G.Y., Jiang, S.H., Yang, J.F.: A TVSCAD approach for image deblurring with impulse noise. Inverse Probl. 33(12), 125008 (2017)

    Article  Google Scholar 

  13. Hitchcock, F.L.: The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 6, 164–189 (1927)

    Article  Google Scholar 

  14. Hong, M.Y., Luo, Z.Q., Razaviyayn, M.: Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM J. Optim. 26(1), 337–364 (2016)

    Article  MathSciNet  Google Scholar 

  15. Jiang, Q., Ng, M.: Robust low-tubal-rank tensor completion via convex optimization. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 2649–2655 (2019)

  16. Karatzoglou, A., Amatriain, X., Baltrunas, L., Oliver, N.: Multiverse recommendation: n-dimensional tensor factorization for context-aware collaborative filtering. In: Proceedings of the fourth ACM Conference on Recommender Systems, pp. 79–86 (2010)

  17. Kilmer, M.W., Braman, K., Hao, N., Hoover, R.C.: Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 34(1), 148–172 (2013)

    Article  MathSciNet  Google Scholar 

  18. Kilmer, M.W., Martin, C.D.: Factorization strategies for third-order tensors. Linear Algebra Appl. 435, 641–658 (2011)

    Article  MathSciNet  Google Scholar 

  19. Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51(3), 455–500 (2009)

    Article  MathSciNet  Google Scholar 

  20. Lathauwer, L.D., Moor, B.D.: From matrix to tensor: multilinear algebra and signal processing. In: McWhirter, J., Proudler, I. (eds.) Mathematics in Signal Processing IV, pp. 1–15. Clarendon Press, Oxford (1998)

    Google Scholar 

  21. Li, Y.F., Shang, K., Huang, Z.H.: Low Tucker rank tensor recovery via ADMM based on exact and inexact iteratively reweighted algorithms. J. Comput. Appl. Math. 331(1), 64–81 (2018)

    Article  MathSciNet  Google Scholar 

  22. Liu, J., Musialski, P., Wonka, P., Ye, J.: Tensor completion for estimating missing values invisual data. IEEE Trans. Pattern Anal. Mach. Intell. 35(1), 208–220 (2013)

    Article  Google Scholar 

  23. Lu, C.Y., Feng, J.S., Chen, Y.D., Liu, W., Lin, Z.C., Yan, S.: Tensor robust principal component analysis with a new tensor nuclear norm. IEEE Trans. Pattern Anal. Mach. Intell. 42(4), 925–938 (2020)

    Article  Google Scholar 

  24. MøRup, M.: Applications of tensor (multiway array) factorizations and decompositions in data mining. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 1(1), 24–40 (2011)

    Article  Google Scholar 

  25. Mu, C., Huang, B., Wright, J., Goldfarb, D.: Square deal: lower bounds and improved relaxations for tensor recovery. In: Proceedings of the 31st International Conference on Machine Learning, vol. 32, pp. 73–81 (2014)

  26. Miao, W.M., Pan, S.H., Sun, D.F.: A rank-corrected procedure for matrix completion with fixed basis coefficients. Math. Program. 159, 289–338 (2016)

    Article  MathSciNet  Google Scholar 

  27. Natarajan, B.K.: Sparse approximate solutions to linear systems. SIAM J. Comput. 24(2), 227–234 (1995)

    Article  MathSciNet  Google Scholar 

  28. Patwardhan, K.A., Sapiro, G., Bertalmio, M.: Video inpainting under constrained camera motion. IEEE Trans. Image Process. 16(2), 545–553 (2007)

    Article  MathSciNet  Google Scholar 

  29. Rockafellar, R.T., Wets, R.J.: Variational Analysis. Springer, Berlin (1997)

    MATH  Google Scholar 

  30. Romera-Paredes, B., Pontil, M.: A new convex relaxation for tensor completion. In: Proceedings of Advances in Neural Informance Processing Systems, vol. 26, pp. 2967–2975 (2013)

  31. Salakhutdinov, R., Srebro, N.: Collaborative filtering in a non-uniform world: learning with the weighted trace norm. In: Proceedings of Advances in Neural Informance Processing Systems, vol. 23,pp. 2056–2064 (2010)

  32. Sauve, A.C., Hero, A.O., Rogers, W.L., Wilderman, S.J., Clinthorne, N.H.: 3D image reconstruction for a compton spect camera model. IEEE Trans. Nucl. Sci. 46(6), 2075–2084 (1999)

    Article  Google Scholar 

  33. Semerci, O.S., Hao, N., Kilmer, M.E., Miller, E.L.: Tensor-based formulation and nuclear norm regularization for multienergy computed tomography. IEEE Trans. Image Process. 23(4), 1678–1693 (2014)

    Article  MathSciNet  Google Scholar 

  34. Signoretto, M., Dinh, Q.T., Lathauwer, L.D., Suykens, J.A.K.: Learning with tensors: a framework based on convex optimization and spectral regularization. Mach. Learn. 94, 303–351 (2014)

    Article  MathSciNet  Google Scholar 

  35. Sun, T., Yin, P.H., Cheng, L.Z., Jiang, H.: Alternating direction method of multipliers with difference of convex functions. Adv. Comput. Math. 44, 723–744 (2018)

    Article  MathSciNet  Google Scholar 

  36. Tao, P.D., An, L.T.H.: Convex analysis approach to D.C. programming: theory, algorithms and applications. Acta Math. Vietnam. 22, 289–355 (1997)

    MathSciNet  MATH  Google Scholar 

  37. Tao, P.D.: Convergence of a subgradient method for computing the bound norm of matrices. Linear Algebra Appl. 62, 163–182 (1984)

    Article  MathSciNet  Google Scholar 

  38. Tao, P.D., Bernoussi, S.E.: Algorithms for solving a class of nonconvex optimization problems. Methods of subgradients. North-Holl. Math. Stud. 129, 249–271 (1986)

    Article  MathSciNet  Google Scholar 

  39. Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31(3), 279–311 (1966)

    Article  MathSciNet  Google Scholar 

  40. Wang, Y., Yin, W.T., Zeng, J.S.: Global convergence of ADMM in nonconvex nonsmooth optimization. J. Sci. Comput. 78, 29–63 (2019)

    Article  MathSciNet  Google Scholar 

  41. Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13(4), 600–612 (2004)

    Article  Google Scholar 

  42. Wright, J., Peng, Y., Ma, Y., Ganesh, A., Rao, S.: Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization. In: Proceedings of Advances in Neural Informance Processing Systems, vol. 22, pp. 2080–2088 (2009)

  43. Yang, L., Pong, T.K., Chen, X.J.: Alternating direction method of multipliers for a class of nonconvex and nonsmooth problems with applications to background/foreground extraction. SIAM J. Imaging Sci. 10(1), 74–110 (2017)

    Article  MathSciNet  Google Scholar 

  44. Yang, Y.N., Feng, Y.L., Suykens, J.A.K.: Robust low-rank tensor recovery with regularized redescending m-estimator. IEEE Trans. Neural Netw. Learn. Syst. 27(9), 1933–1946 (2016)

    Article  MathSciNet  Google Scholar 

  45. Zhang, C.H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38(2), 894–942 (2010)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Professor Yuning Yang for sending us the code of the W-ST in [44].

Author information

Authors and Affiliations

  1. School of Mathematics, Hunan University, Changsha, 410082, Hunan, People’s Republic of China

    Xueying Zhao & Minru Bai

  2. Department of Mathematics, The University of Hong Kong, Pok Fu Lam, Hong Kong

    Michael K. Ng

Authors
  1. Xueying Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Minru Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael K. Ng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Minru Bai.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Minru Bai: Research supported in part by the National Natural Science Foundation of China under Grant 11971159.

Michael K. Ng: Research supported in part by the HKRGC GRF 12306616, 12200317, 12300218, 12300519, 17201020, and HKU Grant 104005583.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, X., Bai, M. & Ng, M.K. Nonconvex Optimization for Robust Tensor Completion from Grossly Sparse Observations. J Sci Comput 85, 46 (2020). https://doi.org/10.1007/s10915-020-01356-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01356-0

Keywords

Mathematics Subject Classification

Search

Navigation