Renormalization Theory of a Two Dimensional Bose Gas: Quantum Critical Point and Quasi-Condensed State

Abstract

We present a renormalization group construction of a weakly interacting Bose gas at zero temperature in the two-dimensional continuum, both in the quantum critical regime and in the presence of a condensate fraction. The construction is performed within a rigorous renormalization group scheme, borrowed from the methods of constructive field theory, which allows us to derive explicit bounds on all the orders of renormalized perturbation theory. Our scheme allows us to construct the theory of the quantum critical point completely, both in the ultraviolet and in the infrared regimes, thus extending previous heuristic approaches to this phase. For the condensate phase, we solve completely the ultraviolet problem and we investigate in detail the infrared region, up to length scales of the order $(\lambda ^3\rho _0)^{-1/2}$ (here $\lambda$ is the interaction strength and $\rho _0$ the condensate density), which is the largest length scale at which the problem is perturbative in nature. We exhibit violations to the formal Ward Identities, due to the momentum cutoff used to regularize the theory, which suggest that previous proposals about the existence of a non-perturbative non-trivial fixed point for the infrared flow should be reconsidered.

Appendices

Appendix 1: Ultraviolet Flow in the Condensate Phase

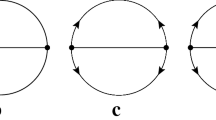
In this section we prove Eqs.(3.29)–(3.30). We denote by $\bar{z}_h$ and $\delta \nu _h$ the quantities defined via the second and third lines of (3.27), both for $h\ge 0$ and ${\bar{h}}\le h<0$. The graphs contributing to $\delta \nu _h$ are all and only ladder diagrams as in the first line of Fig. 12, for all $h\ge {\bar{h}}$; those contributing to $\bar{z}_h$ are all and only ladder diagrams as in the second line of Fig. 12, if $h\ge 0$, while they can be either as in the second line of Fig. 12 or as in Fig. 13, if ${\bar{h}}\le h<0$. For both couplings, we distinguish the regime $h\ge 0$ from ${\bar{h}}\le h<0$.

Let us first consider $\delta \bar{\nu }_h$. If $h\ge 0$ we proceed as in the “ultraviolet regime” subsection of Sect. 2.4, thus obtaining a bound on the $n$-th order diagrams of the same form as the $n$-th order term in the right side of (2.61). Since $n\ge 2$, we find that $|\delta \bar{\nu }_h|\le C \lambda ^2\gamma ^{-h}$ for all $h\ge 0$. For $h<0$ we write the beta function equation for $\delta \bar{\nu }_h$, analogous to (2.63), with initial datum $\delta \bar{\nu }_0$ of the order $\lambda ^2$: $\delta \bar{\nu }_{h-1}=\delta \bar{\nu }_h+\beta _h^{\delta \bar{\nu }}$, with $h\le 0$. Using the (renormalized analogoue of) (3.20), we see that $|\beta _h^{\delta \bar{\nu }}|\le C\lambda ^2$, $\forall {\bar{h}}\le h\le 0$, which implies that $|\delta \bar{\nu }_h|\le C\lambda ^2|h|$, $\forall {\bar{h}}\le h\le 0$, as desired.

We now apply the same strategy to the study of the flow of $\bar{z}_h$. If $h\ge 0$, we find that the diagrams of order $n$ are bounded by $\lambda (K\lambda )^{n-1}\gamma ^{{\bar{h}}-h}$, with $n\ge 1$; here the factor $\gamma ^{{\bar{h}}-h}$ is a dimensional estimate on the $L_\infty$ norm of the off diagonal propagator $r_h$. Therefore, $|\bar{z}_h|\le (\mathrm{const.})\lambda \gamma ^{{\bar{h}}-h}$, for all $h\ge 0$. In particular, $\bar{z}_0$ is of order $\lambda ^2$. From smaller scales, we study again the beta function equation $\bar{z}_{h-1}=\bar{z}_h+\beta _h^{\bar{z}}$, where $|\beta _h^{\bar{z}}|\le C\lambda ^2$, for all ${\bar{h}}\le h\le 0$ (see Fig. 16 for a graphical representation of the first non trivial contribution to $\beta _h^{\bar{z}}$). Therefore, as for $\delta \bar{\nu }_h$, we find $|\bar{z}_h|\le C\lambda ^2|h|$, $\forall {\bar{h}}\le h\le 0$, which concludes the proof of (3.29)–(3.30).

Fig. 16

Feynman diagrams representation of the first non trivial contribution to the beta function of $\bar{z}_{h-1}$, of $h\le -1$

Appendix 2: Bounds on the Propagators

In this section we prove the decay bound (3.39). We first focus on ${\tilde{g}}^{(1)}_{\bar{h}}$. Of course, it is enough that we restrict to its $-+$ component, which we rewrite as the sum of two terms, whose definition is induced by the following rewriting of the cutoff function appearing under the integral sign in (3.42):

$$\begin{aligned}&1-\chi \big (\gamma ^{\bar{h}}(x_0^2+|{\vec {x}}|^4)^{1/2} \big )-\chi \big (\gamma ^{-{\bar{h}}}(k_0^2+|{\vec {k}}|^4)^{1/2}\big ) \equiv (1-{\mathfrak {h}}_{{\bar{h}}}(\mathbf{x}))\big (1 -{\tilde{\chi }}_{\bar{h}}(\mathbf{k})\big )-{\mathfrak {h}}_{{\bar{h}}}(\mathbf{x}) {\tilde{\chi }}_{\bar{h}}(\mathbf{k}) \end{aligned}$$

(6.1)

where

$$\begin{aligned} {\mathfrak {h}}_{{\bar{h}}}(\mathbf{x}) = \chi \big (\gamma ^{\bar{h}}(x_0^2+|{\vec {x}}|^4)^{1/2} \big ),&{\tilde{\chi }}_{\bar{h}}(\mathbf{k}) = \chi \big (\gamma ^{-{\bar{h}}}(k_0^2+|{\vec {k}}|^4)^{1/2} \big ). \end{aligned}$$

(6.2)

The corresponding decomposition for the $-+$ component of $\tilde{g}^{(1)}_{\bar{h}}$ is $[{\tilde{g}}^{(1)}_{{\bar{h}}}(\mathbf{x})]_{-+}= g_{\bar{h}}^{(1a)}(\mathbf{x}) - g_{\bar{h}}^{(1b)}(\mathbf{x})$. We now show that the two terms separately satisfy the same bound as (3.39). The easiest term to treat is $g_{\bar{h}}^{(1b)}(\mathbf{x})$, which we write as

$$\begin{aligned} g_{\bar{h}}^{(1b)}(\mathbf{x})={\mathfrak {h}}_{\bar{h}}(\mathbf{x})\int \frac{d\mathbf{k}}{(2\pi )^3} e^{-i\mathbf{k}\mathbf{x}}\frac{{\tilde{\chi }}_{\bar{h}}(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}. \end{aligned}$$

(6.3)

Using the compact support properties of ${\tilde{\chi }}_{\bar{h}}(\mathbf{k})$, it is immediate to check that

$$\begin{aligned} \big | {\tilde{g}}_{{\bar{h}}}^{(1b)}(\mathbf{x}) \big |&={\mathfrak {h}}_{\bar{h}}(\mathbf{x}) \bigg | \int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}} \frac{{\tilde{\chi }}_{\bar{h}}(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg | \le (\mathrm{const}.) \gamma ^{{\bar{h}}}{\mathfrak {h}}_{\bar{h}}(\mathbf{x})\,, \end{aligned}$$

(6.4)

which implies (3.39) for $n_0=|{\vec {n}}|=0$. In order to estimate the derivatives of ${\tilde{g}}_{{\bar{h}}}^{(1b)}(\mathbf{x})$, note that each derivative $\partial _{x_0}$ (resp. $\partial _{x_i}$ with $i=1,2$) acting on ${\mathfrak {h}}_{\bar{h}}(\mathbf{x})$ produces a factor proportional to $\gamma ^{{\bar{h}}}$ (resp. $\gamma ^{{\bar{h}}/2}$), as desired. Moreover, each derivative $\partial _{x_0}$ (resp. $\partial _{x_i}$ with $i=1,2$) acting on the integral in the right side of (6.3) produces a factor $-ik_0$ (resp. $-ik_i$) under the integral sign, which is bounded proportionaly to $\gamma ^{{\bar{h}}}$ (resp. $\gamma ^{{\bar{h}}/2}$), thanks to the compact support properties of $\tilde{\chi }_{\bar{h}}$. This concludes the proof that $\tilde{g}^{(1b)}_{\bar{h}}$ satisfies a bound like (3.39).

Let us now focus on $\tilde{g}_{\bar{h}}^{(1a)}(\mathbf{x})$. In order to bound it, we rewrite the cutoff function $(1-{\tilde{\chi }}_{\bar{h}}(\mathbf{k}))$ appearing in its definition as $\sum _{h> {\bar{h}}} {\mathfrak {f}}_h(\mathbf{k})$, with ${\mathfrak {f}}_h(\mathbf{k})$ defined after (3.17) and note that, thanks to compact support properties of ${\mathfrak {f}}_h$,

$$\begin{aligned} \bigg | \partial _{x_0}^{n_0}\partial _{{\vec {x}}}^{{\vec {n}}}\int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}} \frac{{\mathfrak {f}}_h(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg | \le C_{n_0,{\vec {n}}} \gamma ^{h(1+n_0+|{\vec {n}}|/2)}\,. \end{aligned}$$

(6.5)

Moreover, integrating by parts and using again the compact support properties of ${\mathfrak {f}}_h$, we find

$$\begin{aligned} |x_0|^N \bigg | \int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}} \frac{{\mathfrak {f}}_h(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg |= \bigg | \int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}}\partial _{k_0}^N \frac{{\mathfrak {f}}_h(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg | \le C_{N} \gamma ^{h(1-N)}\nonumber \\ \end{aligned}$$

(6.6)

and, similarly,

$$\begin{aligned} |{\vec {x}}|^N \bigg | \int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}} \frac{{\mathfrak {f}}_h(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg | \le C_{N} \gamma ^{h(1-N/2)}. \end{aligned}$$

(6.7)

Combining the previous three equations we find

$$\begin{aligned} \bigg | \partial _{x_0}^{n_0}\partial _{{\vec {x}}}^{{\vec {n}}}\int \frac{d^{3}\mathbf{k}}{(2\pi )^{3}} e^{-i \mathbf{k}\cdot \mathbf{x}} \frac{{\mathfrak {f}}_h(\mathbf{k})}{-ik_0+|{\vec {k}}|^2}\bigg | \le C_{N,n_0,{\vec {n}}} \frac{\gamma ^{h(1+n_0+|{\vec {n}}|/2)}}{1+[\gamma ^h(|x_0|+|{\vec {x}}|^2)]^N} \,, \end{aligned}$$

(6.8)

which leads to

$$\begin{aligned} \big | \partial _{x_0}^{n_0}\partial _{{\vec {x}}}^{{\vec {n}}}\tilde{g}^{(1a)}_{\bar{h}}(\mathbf{x})\big |\le C_{N,n_0,{\vec {n}}}(1-{\mathfrak {h}}_{\bar{h}}(\mathbf{x}))\sum _{h>{\bar{h}}} \frac{\gamma ^{h(1+n_0+|{\vec {n}}|/2)}}{1+[\gamma ^h(|x_0|+|{\vec {x}}|^2)]^N}. \end{aligned}$$

(6.9)

Now, on the support of $(1-{\mathfrak {h}}_{\bar{h}}(\mathbf{x}))$, the combination $(|x_0|+|{\vec {x}}|^2)$ is larger than (const.)$\gamma ^{{\bar{h}}}$ and, therefore, for all $N_1,N_2\ge 0$ such that $N_1+N_2=N$,

$$\begin{aligned} \big | \partial _{x_0}^{n_0}\partial _{{\vec {x}}}^{{\vec {n}}}\tilde{g}^{(1a)}_{\bar{h}}(\mathbf{x})\big |\le C_{N,n_0,{\vec {n}}}'(1-{\mathfrak {h}}_{\bar{h}}(\mathbf{x}))\sum _{h>{\bar{h}}} \frac{\gamma ^{({\bar{h}}-h)N_1}\gamma ^{h(1+n_0+|{\vec {n}}|/2)}}{1+[\gamma ^h(|x_0|+|{\vec {x}}|^2)]^{N_2}}, \end{aligned}$$

(6.10)

which is summable over $h$ as soon as $N_1>n_0+|{\vec {n}}|/2$. By picking such an $N_1$ we obtain the desired bound on $\tilde{g}^{(1a)}_{\bar{h}}$.

The proof of the desired decay bound for $\tilde{g}^{(2)}_{\bar{h}}$ is completely analogous to the proof of (6.8) and, therefore, we do not give its details here. The same is true for the proof of (3.43), which we also leave to the reader.

Appendix 3: Lowest Order Computations

In this section we prove (3.81)–(3.83) and (3.89)–(3.92), i.e., we explicitly compute the beta functions for $\lambda _h$, $\mu _h$, $\nu _h$, $Z_h$, $E_h$, $B_h$ and $A_h$ at the lowest non-trivial order (which turns out to coincide with the one-loop computation). Rather than presenting the computations in the same order as we presented the formulas after (3.81), we proceed in order of increasing difficulty, starting from the easiest computation, which is the beta function of $Z_h$, then moving to the beta function of $\nu _h$, etc.

In the following, in the computation of the one-loop contributions to the beta function, we systematically perform a number of approximations, which either induce corrections of higher order than the one we are computing, or are dimensionally irrelevant for $h\le {\bar{h}}$. The approximations we do are the following: (1) we systematically replace $\gamma ^{h+1}\lambda _{h+1}$ by $\gamma ^{h}\lambda _h$, $\gamma ^{(h+1)/2}\mu _{h+1}$ by $\gamma ^{h/2}\mu _h$, $\gamma ^{2(h+1)}\nu _{h+1}$ by $\gamma ^{2h}\nu _h$, $A_{h+1}$ by $A_h$, $B_{h+1}$ by $B_h$, $E_{h+1}$ by $E_h$, and $Z_{h+1}$ by $Z_h$, since these replacements induce an error that is of higher order in $\lambda$; (2) similarly, we replace the renormalization functions $\tilde{A}_{h-1}(\mathbf{k})$, etc, appearing in the definition of the propagator on scale $h$ by $A_h$, etc; moreover, recalling the definition of $\chi _h(\mathbf{k})$ in (3.51), we replace the support function $\tilde{f}_h(\mathbf{k})=\chi _h(\mathbf{k})-\chi _{h-1}(\mathbf{k})$ by ${\mathfrak {f}}_h(|\mathbf{k}'|):=\chi (\gamma ^{-h}|\mathbf{k}'|)-\chi (\gamma ^{-h+1}|\mathbf{k}'|)$, where with some abuse of notation we let $\mathbf{k}':=(k_0,\sqrt{A_h/C_h}\,{\vec {k}})\equiv (k_0,{\vec {k}}')$; note that also these replacements induce errors of higher order in $\lambda$; (3) finally, we systematically neglect the terms coming from trees with at least one endpoint on scale ${\bar{h}}$, since these terms have relative size $\gamma ^{\theta (h-{\bar{h}})}$ with $0<\theta <1$ as compared to the main contributions to the beta function (see (3.75)).

1.1 Appendix 3.1: Lowest Order Beta Function for $Z_h$

The lowest order contribution to $\beta _{h}^{Z}$ (see (3.80) and (3.63)) is of order $\lambda _h$ (or, equivalently, of order $\mu _h^2$) and can be represented graphically by diagrams of the form in Fig. 17, computed at zero external momentum, with the two propagators labelled by two scale labels $h_1,h_2$ such that $\min \{h_1,h_2\}=h$. Note that by the compact support properties of the propagator $|h_1-h_2|\le 1$. The sum of the values of these diagrams is

$$\begin{aligned} \beta _{h}^{Z} = -2 \int \frac{d\mathbf{k}}{(2\pi )^3}\Big [\gamma ^h\mu _h^2\big (\hat{\tilde{g}}_{tt}^{(h)}(\mathbf{k})\big )^2+2\gamma ^{h+1}\mu _{h+1}^2\hat{\tilde{g}}^{(h)}_{tt}(\mathbf{k})\hat{\tilde{g}}^{(h+1)}_{tt}(\mathbf{k})\Big ], \end{aligned}$$

(7.1)

where

$$\begin{aligned} \hat{{\tilde{g}}}^{(h)}_{tt}(\mathbf{k})= \frac{ {\tilde{f}}_{h}(\mathbf{k})}{\tilde{C}_{h-1}(\mathbf{k}) \big [k_0^2+({\tilde{A}}_{h-1}(\mathbf{k})/{\tilde{C}}_{h-1}(\mathbf{k}))|{\vec {k}}|^2\big ]}, \end{aligned}$$

(7.2)

where ${\tilde{Z}}_{h-1}(\mathbf{k})\tilde{C}_{h-1}(\mathbf{k})={\tilde{Z}}_{h-1}(\mathbf{k})\tilde{B}_{h-1}(\mathbf{k})+\tilde{E}_{h-1}^2(\mathbf{k})$. Under the approximations explained above, this propagator can be replaced by

$$\begin{aligned} \bar{g}^{(h)}_{tt}(\mathbf{k}')= {\mathfrak {f}}_{h}(|\mathbf{k}'|)\,\frac{ 1}{C_h|\mathbf{k}'|^2}. \end{aligned}$$

(7.3)

For future reference, let us write down the analogues of this equation, as far as the propagators with labels $lt$ and $ll$ are concerned:

$$\begin{aligned} \bar{g}^{(h)}_{ll}(\mathbf{k}')= {\mathfrak {f}}_{h}(|\mathbf{k}'|)\,\frac{B_h k_0^2+C_h|{\vec {k}}'|^2}{Z_hC_h|\mathbf{k}'|^2},\qquad \bar{g}^{(h)}_{lt}(\mathbf{k})={\mathfrak {f}}_{h}(|\mathbf{k}'|)\,\frac{E_h k_0}{Z_hC_h|\mathbf{k}'|^2}. \end{aligned}$$

(7.4)

Using these replacements, as well as the ones spelled above, we find that (7.1) is equal (up to higher order corrections) to

$$\begin{aligned} \beta _{h}^{Z} = -2\gamma ^h\mu _h^2\frac{1}{A_h C_h}\int \frac{d\mathbf{k}}{(2\pi )^3}\frac{{\mathfrak {f}}^2_h(|\mathbf{k}|) + 2{\mathfrak {f}}_h(|\mathbf{k}|){\mathfrak {f}}_{h+1}(|\mathbf{k}|)}{|\mathbf{k}|^4}, \end{aligned}$$

(7.5)

so that after rescaling and after the change of variables $k_0=\rho \cos \vartheta$, $|{\vec {k}}|=\rho \sin \vartheta$, with $\rho \ge 0$ and $\vartheta \in [0, \pi ]$, we get

$$\begin{aligned} \beta _{h}^{Z} = -2 \frac{1}{A_h C_h}\, \mu _h^2\, \frac{1}{2\pi ^2} \int \frac{d\rho }{\rho ^2}\, \big ({\mathfrak {f}}^2_0(\rho ) +2{\mathfrak {f}}_0(\rho ){\mathfrak {f}}_1(\rho ) \big ), \end{aligned}$$

(7.6)

which is the same as (3.89).

Fig. 17

Leading order beta function for $Z_h$. The graph represents the lowest order contribution to ${\hat{W}}^{(h)}_{2,0}(\mathbf{0})$, and the two solid lines (associated with two propagators of type $\tilde{g}_{tt}^{(h_i)}$) come with two labels $h_1,h_2$, which we need to sum over, with the constraints that $\min \{h_1,h_2\}=h$ and $|h_1-h_2|\le 1$

1.2 Appendix 3.2: Lowest Order Beta Function for $\nu _h$

The lowest order contributions to $\beta _h^\nu$ (see (3.78) and (3.59)) are of the order $\lambda _h$ and can be represented graphically as in Fig. 18. Once again, the propagators are associated with scale labels such that the minimum scale is equal to $h$. We denote by $\beta ^{\nu ,(1)}_h$ the contribution from the first diagram in Fig. 18, and by $\beta ^{\nu ,(2)}_h$ those from the last two diagrams. Proceeding as in the previous section we find that, up to higher order corrections,

$$\begin{aligned} \gamma ^{2h -{\bar{h}}}\beta ^{\nu ,(1)}_h = 6\, \frac{1}{A_h}\, \gamma ^{h -{\bar{h}}} \lambda _h \int \frac{d^3 \mathbf{k}}{(2\pi )^3} \frac{{\mathfrak {f}}_h(|\mathbf{k}|)}{|\mathbf{k}|^2} = 6\, \frac{1}{A_h}\, \gamma ^{2h -{\bar{h}}} \lambda _h \,\frac{1}{2\pi ^2} \int d\rho \, {\mathfrak {f}}_0(\rho ). \end{aligned}$$

(7.7)

In order to calculate $\beta ^{\nu ,(2)}_h$ we notice that the sum of the remaining two diagrams in Fig. 18 involves the following combinations of propagators (after the usual replacements):

$$\begin{aligned} \bar{g}^{(h)}_{tt}(\mathbf{k})\bar{g}^{(h)}_{ll}(\mathbf{k}) + \bigl (\bar{g}^{(h)}_{tl}(\mathbf{k})\bigr )^2&= \frac{{\mathfrak {f}}^2_h(|\mathbf{k}|) }{Z_h C_h |\mathbf{k}|^2} \end{aligned}$$

(7.8)

$$\begin{aligned} \bar{g}^{(h)}_{tt}(\mathbf{k})\bar{g}^{(h+1)}_{ll}(\mathbf{k}) +\bar{g}^{(h+1)}_{tt}(\mathbf{k})\bar{g}^{(h)}_{ll}(\mathbf{k}) + 2\bar{g}^{(h)}_{tl}(\mathbf{k})\bar{g}^{(h+1)}_{tl}(\mathbf{k})&= \frac{ 2 {\mathfrak {f}}_h(|\mathbf{k}|) {\mathfrak {f}}_{h+1}(|\mathbf{k}|) }{Z_h C_h |\mathbf{k}|^2}+h.o., \end{aligned}$$

(7.9)

where $h.o.$ in the last equation means “higher orders”. Using these identities we find, up to higher order corrections:

$$\begin{aligned} \gamma ^{2h-{\bar{h}}}\beta ^{\nu ,(2)}_h&= -2\, \gamma ^{2h} \frac{\mu ^2_h}{Z_h}\, \frac{1}{A_h}\,\int \frac{d^3 \mathbf{k}}{(2\pi )^3} \frac{{\mathfrak {f}}^2_0(|\mathbf{k}|) +2{\mathfrak {f}}_0(|\mathbf{k}|) {\mathfrak {f}}_{1}(|\mathbf{k}|)}{ |\mathbf{k}|^2} \nonumber \\&= -2\, \gamma ^{2h} \frac{\mu ^2_h}{Z_h}\, \frac{1}{A_h}\,\frac{1}{2\pi ^2}\int d\rho \big ({\mathfrak {f}}^2_0(\rho ) + 2{\mathfrak {f}}_0(\rho ){\mathfrak {f}}_1(\rho )). \end{aligned}$$

(7.10)

Putting things together:

$$\begin{aligned} \beta ^{\nu }_h&= \bigg ( 6\lambda _h - 2\mu ^2_h\frac{\gamma ^{{\bar{h}}}}{Z_h} \bigg )\frac{1}{A_h}\, \,\frac{1}{2\pi ^2} \int d\rho \, {\mathfrak {f}}_0(\rho )\, \nonumber \\&-2\, \mu ^2_h\frac{\gamma ^{\bar{h}}}{Z_h}\, \frac{1}{A_h}\,\frac{1}{2\pi ^2}\int d\rho \big ({\mathfrak {f}}^2_0(\rho ) + 2{\mathfrak {f}}_0(\rho ){\mathfrak {f}}_1(\rho ) - {\mathfrak {f}}_0(\rho ) \big ). \end{aligned}$$

(7.11)

Using the definitions (3.84)–(3.88), this can be rewritten as

$$\begin{aligned} \beta ^{\nu }_h = \bigg ( 6\lambda _h - 2\mu ^2_h\frac{\gamma ^{{\bar{h}}}}{Z_h} \bigg )\frac{1}{A_h}\, \beta ^{(1)}_0 -2\, \mu ^2_h\frac{\gamma ^{\bar{h}}}{Z_h}\, \frac{1}{A_h}\beta _0^{(1,\chi )} , \end{aligned}$$

(7.12)

which implies (3.83).

Fig. 18

Leading order beta function for $\nu _h$

1.3 Appendix 3.3: Lowest Order Beta Function for $\mu _h$

The lowest order contributions to $\beta _h^\mu$ are of the order $\mu _h\lambda _h$ and can be represented graphically as in Fig. 19. Once again, the propagators are associated with scale labels such that the minimum scale is equal to $h$. We denote by $\beta _h^{\mu ,(2) }$ (resp. $\beta _h^{\mu ,(3)}$) the contribution to $\beta _h^{\mu }$ coming from the first diagram (resp. second $+$ third $+$ fourth diagrams) in Fig. 19. We find:

$$\begin{aligned} \gamma ^{\frac{h}{2}} \beta _h^{\mu ,(2) }&= - 12\, \frac{1}{A_h C_h}\, \gamma ^{\frac{h}{2}} \mu _h \gamma ^{h -{\bar{h}}}\lambda _h \,\int \frac{d^3 \mathbf{k}}{(2\pi )^3} \frac{{\mathfrak {f}}^2_h(|\mathbf{k}|) + 2{\mathfrak {f}}_h(|\mathbf{k}|) {\mathfrak {f}}_{h+1}(|\mathbf{k}|)}{|\mathbf{k}|^4} \nonumber \\&= - 12\, \frac{1}{A_h C_h \gamma ^{\bar{h}}}\, \gamma ^{\frac{h}{2}} \mu _h \lambda _h\,\beta _0^{(2)}, \end{aligned}$$

(7.13)

and, using the analogues of (7.8)–(7.9),

$$\begin{aligned} \gamma ^{\frac{h}{2}} \beta _h^{\mu , (3)}&= 4 \,\frac{C_h}{A_h} \gamma ^{\frac{3}{2}h} \mu _h^3 \,\int \frac{ d^3\mathbf{k}}{(2\pi )^3}\, \frac{1}{Z_h C^2_h |\mathbf{k}|^4}\nonumber \\&\quad \quad \left[ {\mathfrak {f}}_h^3(|\mathbf{k}|) +3 {\mathfrak {f}}_h^2(|\mathbf{k}|) {\mathfrak {f}}_{h+1}(|\mathbf{k}|) +3 {\mathfrak {f}}_h(|\mathbf{k}|) {\mathfrak {f}}^2_{h+1}(|\mathbf{k}|) \right] \nonumber \\&= 4 \,\frac{1}{A_h C_h}\, \gamma ^{\frac{h}{2}} \frac{\mu _h^3}{Z_h}\,\frac{1}{2\pi ^2} \int \frac{d\rho }{\rho ^2}\, \left[{\mathfrak {f}}^3_0(\rho ) +3{\mathfrak {f}}_0^2(\rho ){\mathfrak {f}}_1(\rho ) + 3{\mathfrak {f}}_0(\rho ) {\mathfrak {f}}_1^2(\rho )\right] \end{aligned}$$

(7.14)

In the last expression, we can rewrite

$$\begin{aligned} \frac{1}{2\pi ^2} \int \frac{d\rho }{\rho ^2}\, \left[{\mathfrak {f}}^3_0(\rho ) +3{\mathfrak {f}}_0^2(\rho ){\mathfrak {f}}_1(\rho ) + 3{\mathfrak {f}}_0(\rho ) {\mathfrak {f}}_1^2(\rho )\right] =\beta _0^{(2)}-\beta _0^{(2,\chi )} \end{aligned}$$

(7.15)

where $\beta _0^{(2,\chi )}$ is defined as in (3.87), so that, putting things together,

$$\begin{aligned} \beta _h^{\mu }&= \frac{1}{A_h C_h\gamma ^{\bar{h}}}\, \bigg [\mu _h \Big (-12 \lambda _h + 4 \mu _h^2 \,\frac{\gamma ^{\bar{h}}}{Z_h}\Big ) \,\beta _0^{(2)} -4 \, \mu ^3_h\, \frac{\gamma ^{\bar{h}}}{Z_h}\,\beta ^{(2,\chi )}_h \bigg ]. \end{aligned}$$

(7.16)

which implies (3.82)

Fig. 19

Leading order beta function for $\mu _h$

1.4 Appendix 3.4: Lowest Order Beta Function for $\lambda _h$

The lowest order contributions to $\beta _h^\lambda$ are of the order $\lambda _h^2$ and can be represented graphically as in Fig. 20. We denote with $\beta ^{\lambda ,(2)}_h$, $\beta ^{\lambda , (3)}_h$ and $\beta ^{\lambda , (4)}_h$ the contributions to $\beta _h^\lambda$ coming from the diagrams in Fig. 20 with two, three and four end-points, respectively. Proceeding as in the previous sections, we find:

$$\begin{aligned} \gamma ^{h-{\bar{h}}}\beta ^{\lambda ,(2)}_h&= -36 \frac{1}{A_h C_h}\, \gamma ^{h -2{\bar{h}}} \lambda ^2_h \, \beta _0^{(2)} ,\end{aligned}$$

(7.17)

$$\begin{aligned} \gamma ^{h-{\bar{h}}}\beta ^{\lambda , (3)}_h&= 24\, \frac{1}{A_h C_h}\, \gamma ^{h-{\bar{h}}} \lambda _h\,\frac{\mu _h^2}{Z_h} \big (\beta _0^{(2)} - \beta _0^{(2,\chi )} \big ), \end{aligned}$$

(7.18)

and

$$\begin{aligned} \gamma ^{h-{\bar{h}}}\beta ^{\lambda , (4)}_h = -4 \frac{1}{A_h C_h }\,\gamma ^{h}\, \frac{\mu _h^4}{Z_h^2} \frac{1}{2\pi ^2} \int \frac{d\rho }{\rho ^2}\,T_4(\rho ), \end{aligned}$$

(7.19)

where

$$\begin{aligned} T_{4}(\rho )&= {\mathfrak {f}}^4_0(\rho ) +4{\mathfrak {f}}_0^3(\rho ){\mathfrak {f}}_{1}(\rho ) +6{\mathfrak {f}}_0^2(\rho ){\mathfrak {f}}^2_{1}(\rho ) +4{\mathfrak {f}}_0(\rho ){\mathfrak {f}}^3_{1}(\rho ). \end{aligned}$$

(7.20)

Using the definitions (3.85)–(3.88), it can be checked that

$$\begin{aligned} \frac{1}{2\pi ^2} \int \frac{d\rho }{\rho ^2}\,T_4(\rho )=\beta _0^{(2)}-\beta _0^{(2,\chi )}-\beta _0^{(3,\chi )}, \end{aligned}$$

(7.21)

so that, putting things together,

$$\begin{aligned} \beta _h^\lambda =&\, \frac{1}{A_h C_h \gamma ^{\bar{h}}} \left( -36 \,\lambda ^2_h +24\,\lambda _h \mu _h^2\frac{ \gamma ^{\bar{h}}}{Z_h} -4 \,\mu _h^4 \frac{\gamma ^{2{\bar{h}}}}{Z_h^2} \right) \beta _0^{(2)} \nonumber \\&+\frac{1}{A_h C_h \gamma ^{\bar{h}}}\, \left[\left( -24\,\lambda _h \mu _h^2 \frac{\gamma ^{\bar{h}}}{Z_h} +4 \,\mu _h^4 \frac{\gamma ^{2{\bar{h}}}}{Z_h^2} \right) \beta _0^{(2,\chi )} +4 \, \mu _h^4\frac{\gamma ^{2{\bar{h}}}}{Z_h^2}\beta _0^{(3,\chi )} \right], \end{aligned}$$

(7.22)

which implies (3.81).

Fig. 20

Leading order beta function for $\lambda _h$

1.5 Appendix 3.5: Lowest Order Beta Function for $E_h$

The lowest order contribution to $\beta ^E_h$ (see (3.80) and (3.62)) is of order $\lambda _h$ and is represented graphically in Fig. 21. The value of the graph is (up to higher order corrections):

$$\begin{aligned} \beta ^{E}_h = \beta ^{E}_{h,2}- \beta ^{E}_{h,1} \end{aligned}$$

(7.23)

with

$$\begin{aligned} \beta ^{E}_{h,i}&= 4\,\frac{1}{A_h}\, \mu _h^2\, \frac{E_h}{C_h Z_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} \frac{ k_0 T_i(\mathbf{k})}{|\mathbf{k}|^2} \,\partial _{p_0} \left[ \frac{T_i(\mathbf{k}+\mathbf{p})}{|\mathbf{k}+\mathbf{p}|^2} \right] _{\mathbf{p}={\mathbf{0}}} \nonumber \\&= 2\,\frac{1}{A_h}\, \mu _h^2 \, \frac{E_h}{C_h Z_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} \, k_0 \, \partial _{k_0}\left(\frac{T_i(\mathbf{k})}{|\mathbf{k}|^2}\right)^2 \end{aligned}$$

(7.24)

where $T_2(\mathbf{k}):= {\mathfrak {f}}_0(|\mathbf{k}|) + {\mathfrak {f}}_1(|\mathbf{k}|)$, $T_1(\mathbf{k}):={\mathfrak {f}}_1(|\mathbf{k}|)$. By integrating by parts:

$$\begin{aligned} \beta ^{E}_{h,i}&= -2\,\frac{1}{A_h}\, \mu _h^2\, \frac{E_h}{C_h Z_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} \, \left(\frac{T_i(\mathbf{k})}{|\mathbf{k}|^2}\right)^2 , \end{aligned}$$

(7.25)

so that

$$\begin{aligned} \beta ^{E}_{h} = -2\,\frac{1}{A_h}\,\frac{E_h}{C_h Z_h} \mu _h^2 \beta ^{(2)}_0, \end{aligned}$$

(7.26)

which gives (3.90).

Fig. 21

Leading order beta function for $E_h$. The graph is first computed at external momentum $\mathbf{p}=(p_0,\vec {0})$, then derived w.r.t. $p_0$; after the action of the derivative, the external momentum is set to ${\mathbf {0}}$

1.6 Appendix 3.6: Lowest Order Beta Function for $B_h$

The lowest order contribution to $\beta ^B_h$ (see (3.79) and (3.61)) is of the order $\lambda _h$ and is represented graphically in Fig. 22. The sum of the values of the two graphs is (up to higher order corrections):

$$\begin{aligned} \beta ^B_h = \beta ^B_{h,2} - \beta ^B_{h,1} \end{aligned}$$

(7.27)

where, defining $\alpha _h=\frac{E_h^2}{Z_h C_h}$, and letting $T_1,T_2$ be the same as in the previous section,

$$\begin{aligned} \beta ^B_{h,i} =- 2\, \frac{ \mu _h^2 }{Z_hA_h }\int \frac{d^3\mathbf{k}}{(2\pi )^3} \partial ^2_{p_0} \bigg [ \frac{|\mathbf{k}|^2+\alpha _hk_0p_0}{|\mathbf{k}|^2|\mathbf{k}+\mathbf{p}|^2}T_{i}(\mathbf{k}+ \mathbf{p}) T_{i} (\mathbf{k}) \bigg ]_{\mathbf{p}={\mathbf {0}}} . \end{aligned}$$

(7.28)

Fig. 22

Leading order beta function for $B_h$

By computing explicitly the derivative, and then integrating by parts, we find:

$$\begin{aligned} \beta ^B_{i,h}&= - 2\, \frac{\mu _h^2 }{Z_hA_h } \int \frac{d^3\mathbf{k}}{(2\pi )^3} \bigg [ 2\alpha _h k_0 \frac{T_i(\mathbf{k})}{|\mathbf{k}|^2} \partial _{k_0}\left(\frac{T_i(\mathbf{k})}{|\mathbf{k}|^2}\right) +T_i(\mathbf{k})\partial ^2_{k_0}\left(\frac{T_i(\mathbf{k})}{|\mathbf{k}|^2}\right) \bigg ]\end{aligned}$$

(7.29)

$$\begin{aligned}&= - 2\, \frac{ \mu _h^2 }{Z_hA_h } \int \frac{d^3\mathbf{k}}{(2\pi )^3} \bigg [ -\alpha _h \left(\frac{T_i(\mathbf{k})}{|\mathbf{k}|^2}\right)^2+\partial _{k_0}T_i(\mathbf{k})\Big ( \frac{2k_0T_i(\mathbf{k})}{|\mathbf{k}|^4}-\frac{\partial _{k_0}T_i(\mathbf{k})}{|\mathbf{k}|^2}\Big )\Big ]. \end{aligned}$$

(7.30)

Let us now denote by $\beta ^{B,(1)}_{i,h}$ the contribution associated with the first term in square brackets, and by $\beta ^{B,(2)}_{i,h}$ the rest. We have:

$$\begin{aligned} \beta _h^{B,(1)}=\beta ^{B,(1)}_{2,h}-\beta ^{B,(1)}_{1,h}= 2 \frac{\mu _h^2}{A_h Z_h} \frac{E_h^2}{Z_h C_h} \beta ^{(2)}_0, \end{aligned}$$

(7.31)

which gives the first term in the r.h.s. of (3.91). Similarly, by passing to polar coordinates $k_0=\rho \cos \vartheta$, $|{\vec {k}}|=\rho \sin \vartheta$, with $\vartheta \in [0,\pi ]$, and by explicitly computing the integral over $\vartheta$, we find:

$$\begin{aligned} \beta _h^{B,(2)}&= \beta ^{B,(2)}_{2,h}-\beta ^{B,(2)}_{1,h}\nonumber \\&= \frac{2}{3} \frac{\mu _h^2}{A_h Z_h} (\gamma -1) \frac{1}{2\pi ^2}\int \frac{d\rho }{\rho }\, \Big [ \rho \big (\chi '(\rho )\big )^2 + 2 \chi '(\rho )\, \big (1-\chi (\rho )\big ) \Big ], \end{aligned}$$

(7.32)

which gives the second term in the r.h.s. of (3.91).

1.7 Appendix 3.7: Lowest Order Beta Function for $A_h$

The lowest order contribution to $\beta ^A_h$ is represented graphically in a way similar to Fig. 22, with $\partial _{p_0}^2$ replaced by $\partial _{p_1}^2$. Therefore, $\beta ^A_h = \beta ^A_{h,2} - \beta ^A_{h,1}$, with

$$\begin{aligned} \beta ^A_{h,i} =- 2\, \frac{\mu _h^2 }{Z_hC_h}\, \int \frac{d^3\mathbf{k}}{(2\pi )^3}T_{i} (\mathbf{k}) \partial ^2_{k_1} \left( \frac{T_{i}(\mathbf{k}+ \mathbf{p})}{|\mathbf{k}+\mathbf{p}|^2} \right) \Big |_{\mathbf{p}={\mathbf {0}}} . \end{aligned}$$

(7.33)

On the other hand, the integral in the r.h.s. is invariant under the exchange $k_0 \longleftrightarrow k_1$ and, therefore, using the result of the previous section,

$$\begin{aligned} \beta ^A_{h} =\frac{2}{3} \frac{\mu _h^2}{C_h Z_h} (\gamma -1) \frac{1}{2\pi ^2}\int \frac{d\rho }{\rho }\, \Big [ \rho \big (\chi '(\rho )\big )^2 + 2 \chi '(\rho )\, \big (1-\chi (\rho )\big ) \Big ], \end{aligned}$$

(7.34)

which proves (3.92).

Appendix 4: Ward Identities

1.1 Appendix 4.1: Derivation of the Global Ward Identities

In this section we derive the Ward Identities associated with a phase transformation $\psi ^\pm _\mathbf{x}\rightarrow e^{\pm i\alpha (\mathbf{x})}\psi ^\pm _\mathbf{x}$, with $\alpha (\mathbf{x})\equiv \alpha$. Next, in the following section, we will show how to modify the computation in order to deal with a local phase transformation in which $\alpha (\mathbf{x})$ is a non-trivial function of $\mathbf{x}$. We introduce a sequence of reference models, labelled by an integer $h$, defined in terms of a functional integral similar to (3.18), but with an extra infrared cutoff at a pre-fixed scale $h$ (that, for definiteness, we shall assume to be $\le {\bar{h}}$):

$$\begin{aligned} e^{-|\Lambda |\mathcal F_{h-1}-{\mathcal {W}}^{(h-1)}(\phi )} = \int P_{\ge h}^B(d\psi ) e^{-\bar{V}(\psi +\phi )}. \end{aligned}$$

(8.1)

Here $P_{\ge h}^B(d\psi )$ is the complex gaussian measure with propagator given by the analogue of (3.13), modulo an extra infrared cutoff¹⁴:

$$\begin{aligned} g^B_{\ge h}(\mathbf{x}-\mathbf{y})=\int \limits _{\mathbb R^3} \frac{d\mathbf{k}}{(2\pi )^3}\hat{\chi }_{\ge h}(\mathbf{k}) \frac{e^{-i\mathbf{k}(\mathbf{x}-\mathbf{y})}}{k_0^2+(\varepsilon '({\vec {k}}))^2}\begin{pmatrix}ik_0 +F({\vec {k}})&{} -\lambda \rho _0\hat{v}({\vec {k}})\\ -\lambda \rho _0\hat{v}({\vec {k}})&{} -ik_0+F({\vec {k}})\end{pmatrix} \end{aligned}$$

(8.2)

and $\hat{\chi }_{\ge h}(\mathbf{k})=1-\chi _{h-1}(\mathbf{k})$, where $\chi _{h-1}(\mathbf{k})$ was defined in (3.51). Moreover, $\bar{V}(\psi )$ is given by (3.11) (we dropped the label $\Lambda$, for simplicity). The interest of the definition (8.1) is that the local parts of the kernels of ${\mathcal {W}}^{(h-1)}$, with $h\le {\bar{h}}$, are essentially¹⁵ the same as the local part of the kernels of ${\mathcal {V}}^{(h-1)}+\sum _{k=h}^{{\bar{h}}}{\mathcal {L}}_Q{\mathcal {V}}^{(k)}$, which we computed in Sect. 3.3.2 via a renormalized multiscale construction. Therefore, identities among the kernels of ${\mathcal {W}}^{(h-1)}$ induce identities between the running coupling constants at scales $h\le {\bar{h}}$, which are the relations we are interested in. See Appendix 2 below for a detailed discussion about the connection between ${\mathcal {W}}^{(h-1)}$ and ${\mathcal {V}}^{(h-1)}$.

In order to obtain the desired identities among the kernels of ${\mathcal {W}}^{(h-1)}(\phi )$ it is convenient to preliminarily manipulate the r.h.s. of (8.1). We recall that the Bogoliubov’s reference gaussian measure $P^B(d\psi )$ was obtained by first combining the negative exponential of the first two lines in (3.3) with the free gaussian measure $P^0$, see the discussion after (3.3), and then by performing the c-number substitution $\xi \rightarrow \sqrt{\rho _0}$ spelled out after (3.9). A similar connection is valid, of course, between the cut-offed measures $P_{\ge h}^B(d\psi )$ and $P_{\ge h}^0(d\psi )$, where $P_{\ge h}^0(d\psi )$ is the free gaussian measure with propagator

$$\begin{aligned} \int \frac{d\mathbf{k}}{(2\pi )^3}\hat{\chi }_{\ge h}(\mathbf{k})\frac{e^{-i\mathbf{k}(\mathbf{x}-\mathbf{y})}}{-ik_0+|{\vec {k}}|^2}. \end{aligned}$$

(8.3)

Therefore, we can write:

$$\begin{aligned} P_{\ge h}^B(d\psi )=e^{-|\Lambda |\tilde{f}_h}P_{\ge h}^0(d\psi )e^{-Q^B_h(\psi )}, \end{aligned}$$

(8.4)

where, in the limit $\Lambda \nearrow \mathbb R^3$ (and using the fact that the term in the second line of (3.3) vanishes in this limit),

$$\begin{aligned} Q^B_{\ge h}(\psi )= \frac{\lambda }{2}\rho _0 \int \limits _{\mathrm{supp}\hat{\chi }_{\ge h}} \frac{d\mathbf{k}}{(2\pi )^3} \,\hat{v}({\vec {k}})\,\hat{\chi }_{\ge h}^{-1}(\mathbf{k}) \,(\hat{\psi }^+_\mathbf{k}+\hat{\psi }^-_{-\mathbf{k}}) (\hat{\psi }^+_{-\mathbf{k}}+\hat{\psi }^-_{\mathbf{k}}). \end{aligned}$$

(8.5)

Plugging (8.4) into (8.1), we find:

$$\begin{aligned} e^{-|\Lambda |\mathcal F_{h}-{\mathcal {W}}_{h}(\phi )} = e^{-|\Lambda |\tilde{f}_h}\int P_{\ge h}^0(d\psi ) e^{-Q^B_{\ge h}(\psi )-\bar{V}(\psi +\phi )}. \end{aligned}$$

(8.6)

We now first perform the change of variables $\psi ^\pm _\mathbf{x}\rightarrow e^{\pm i\alpha }\psi ^{\pm }_\mathbf{x}$, and then we derive w.r.t. $\alpha$, so that:

$$\begin{aligned} 0 = \frac{\partial }{\partial \alpha } \int P_{\ge h}^0(d\psi )\, e^{- Q^B_{\ge h}(e^{i\alpha }\psi ) -\bar{V}(e^{i \alpha }\psi +\phi )} \Big |_{\alpha =0}. \end{aligned}$$

(8.7)

In order to compute the derivative explicitly, it is convenient to rewrite $\bar{V}=\bar{W} (\psi )+\bar{Q}(\psi )$ with

$$\begin{aligned} \bar{W}(\psi )&= \frac{\lambda }{2}\int d\mathbf{x}\,d\mathbf{y}\big [|\psi _\mathbf{x}+\sqrt{\rho _0}|^2-\rho _0\big ] w(\mathbf{x}-\mathbf{y}) \big [|\psi _\mathbf{y}+\sqrt{\rho _0}|^2-\rho _0\big ]\end{aligned}$$

(8.8)

$$\begin{aligned}&\quad + \bar{\nu }\int d\mathbf{x}\big [|\psi _\mathbf{x}+\sqrt{\rho _0}|^2-\rho _0\big ],\end{aligned}$$

(8.9)

$$\begin{aligned} \bar{Q}(\psi )&=-\frac{\lambda }{2}\rho _0\int d\mathbf{x}\,d\mathbf{y}\,(\psi ^+_\mathbf{x}+\psi ^-_\mathbf{x})w(\mathbf{x}-\mathbf{y})(\psi ^+_\mathbf{y}+\psi ^-_\mathbf{y})-\bar{\nu }\sqrt{\rho _0}\int d\mathbf{x}(\psi ^+_\mathbf{x}+\psi ^-_\mathbf{x}), \end{aligned}$$

(8.10)

and then note that

$$\begin{aligned}&\frac{\partial }{\partial \alpha } \bar{W}(e^{i \alpha }\psi + \phi ) \Big |_{\alpha =0}\nonumber \\&\quad = -i \int d\mathbf{x}\left[ \frac{\delta \bar{W}(\psi +\phi )}{\delta \phi ^+_\mathbf{x}}\big ( \phi ^+_\mathbf{x}+ \sqrt{\rho _0}\big ) - \frac{\delta \bar{W}(\psi +\phi )}{\delta \phi ^-_\mathbf{x}}\big ( \phi ^-_\mathbf{x}+ \sqrt{\rho _0}\big ) \right], \end{aligned}$$

(8.11)

from which one gets (after an explicit computation of the contributions coming from $\bar{Q}$):

$$\begin{aligned}&\frac{\partial }{\partial \alpha } \bar{V}(e^{i \alpha }\psi + \phi ) \Big |_{\alpha =0}\nonumber \\&\quad = \,- i \int d\mathbf{x}\left[ \frac{\delta \bar{V}(\psi +\phi )}{\delta \phi ^+_\mathbf{x}} \cdot \big ( \phi ^+_\mathbf{x}+ \sqrt{\rho _0}\big ) - \frac{\delta \bar{V}(\psi +\phi )}{\delta \phi ^-_\mathbf{x}} \cdot \big ( \phi ^-_\mathbf{x}+ \sqrt{\rho _0}\big ) \right] \nonumber \\&\qquad -i\lambda \rho _0 \int d\mathbf{x}\, d\mathbf{y}\big (\psi ^+_\mathbf{x}+\phi ^+_\mathbf{x}- \psi ^-_\mathbf{x}- \phi ^-_\mathbf{x}\big )w(\mathbf{x}-\mathbf{y})\big (\psi ^+_\mathbf{y}+ \phi ^+_\mathbf{y}+\psi ^- _\mathbf{y}+ \phi ^-_\mathbf{y}\big )\nonumber \\&\qquad -i\bar{\nu }\sqrt{\rho _0} \int d\mathbf{x}\big (\psi ^+_\mathbf{x}+\phi ^+_\mathbf{x}- \psi ^-_\mathbf{x}- \phi ^-_\mathbf{x}\big ). \end{aligned}$$

(8.12)

Note that the term in the last line is equal to $-i\bar{\nu }\sqrt{\rho _0} \int d\mathbf{x}\big (\phi ^+_\mathbf{x}- \phi ^-_\mathbf{x}\big )$, simply because $\psi$ has zero average, by construction. If we now use (8.12) into (8.7), after an explicit computation of the contribution coming from $\bar{Q}^B_{\ge h}$ we find:

$$\begin{aligned}&\int P_{\ge h}^B(d\psi ) e^{-\bar{V}(\psi +\phi )}\left\{ \int d\mathbf{x}\left[ \frac{\delta \bar{V}(\psi +\phi )}{\delta \phi _{\mathbf{x}}^{+}} \left( \phi _{\mathbf{x}}^{+}+\sqrt{\rho _0}\right) -\frac{\delta \bar{V}(\psi +\phi )}{\delta \phi _{\mathbf{x}}^{-}} \left( \phi _{\mathbf{x}}^{-}+\sqrt{\rho _{0}}\right) \right] \right. \nonumber \\&\quad \left. +\,\lambda \rho _0 \int d\mathbf{x}\, d\mathbf{y}\Big [\big (\psi ^+_\mathbf{x}+\phi ^+_\mathbf{x}- \psi ^-_\mathbf{x}- \phi ^-_\mathbf{x}\big )w(\mathbf{x}-\mathbf{y})\big (\psi ^+_\mathbf{y}+ \phi ^+_\mathbf{y}+\psi ^- _\mathbf{y}+ \phi ^-_\mathbf{y}\big )\right. \nonumber \\&\quad \left. -\,\big (\psi ^+_\mathbf{x}- \psi ^-_\mathbf{x}\big )w_{\ge h}(\mathbf{x}-\mathbf{y})\big (\psi ^+_\mathbf{y}+\psi ^- _\mathbf{y}\big )\Big ] +\bar{\nu }\sqrt{\rho _0} \int d\mathbf{x}\big (\phi ^+_\mathbf{x}- \phi ^-_\mathbf{x}\big )\right\} =0, \end{aligned}$$

(8.13)

where $w_{\ge h}(\mathbf{x})$ is the Fourier transform of $\hat{v}({\vec {k}})[\hat{\chi }_{\ge h}(\mathbf{k})]^{-1}$. The Eq. (8.13) can be rewritten in terms of the fields $\psi ^{l},\psi ^t$ and $\phi ^{l},\phi ^t$ defined via (3.41), in terms of which we find:

$$\begin{aligned} 0=&\int P_{\ge h}^B(d\psi ) e^{-\bar{V}(\psi +\phi )}\left\{ \int d\mathbf{x}\left[ \frac{\delta \bar{V}(\psi +\phi )}{\delta \phi _{\mathbf{x}}^{l}}\phi _{\mathbf{x}}^{t} -\frac{\delta \bar{V}(\psi +\phi )}{\delta \phi _{\mathbf{x}}^{t}} \left( \phi _{\mathbf{x}}^{l}+\sqrt{2\rho _{0}}\right) \right] \right. \nonumber \\&\left. +\,2\lambda \rho _0 \!\!\int d\mathbf{x}\,d\mathbf{y}\Big [\big (\phi ^t_\mathbf{x}+ \psi ^t_\mathbf{x})w(\mathbf{x}-\mathbf{y})\big (\psi ^l_\mathbf{y}+ \phi ^l_\mathbf{y}\big ) -\psi ^t_\mathbf{x}w_{\ge h}(\mathbf{x}-\mathbf{y})\psi ^l_\mathbf{y}\Big ]\right. \nonumber \\&\left. +\,\bar{\nu }\sqrt{2\rho _0}\int d\mathbf{x}\, \phi ^t_\mathbf{x}\right\} . \end{aligned}$$

(8.14)

Defining $\langle [\ \cdot \ ]\rangle _h^\phi =e^{|\Lambda |{\mathcal {F}}_{h-1}+{\mathcal {W}}^{(h-1)}(\phi )}\int P_{\ge h}^B(d\psi ) e^{-\bar{V}(\psi +\phi )}[\ \cdot \ ]$, we can rewrite the last equation as

$$\begin{aligned} 0&= \int d\mathbf{x}\left[ \frac{\delta {\mathcal {W}}^{(h-1)}(\phi )}{\delta \phi _{\mathbf{x}}^{l}}\phi _{\mathbf{x}}^{t} -\frac{\delta {\mathcal {W}}^{(h-1)}(\phi )}{\delta \phi _{\mathbf{x}}^{t}} \left( \phi _{\mathbf{x}}^{l}+\sqrt{2\rho _{0}}\right) \right] +\bar{\nu }\sqrt{2\rho _0}\int d\mathbf{x}\, \langle \phi ^t_\mathbf{x}\rangle _h^\phi \nonumber \\&\quad + 2\lambda \rho _0 \int d\mathbf{x}\,d\mathbf{y}\,w(\mathbf{x}-\mathbf{y}) \langle \big [\big (\phi ^t_\mathbf{x}+ \psi ^t_\mathbf{x})\big (\psi ^l_\mathbf{y}+ \phi ^l_\mathbf{y}\big )-\psi ^t_\mathbf{x}\psi ^l_\mathbf{y}\big ]\rangle _h^\phi -\int d\mathbf{x}\langle \Delta _h(\mathbf{x})\rangle _h^\phi , \end{aligned}$$

(8.15)

where in the second line $\Delta _h(\mathbf{x})$ is the correction due to the presence of the cutoff:

$$\begin{aligned} \Delta _h(\mathbf{x}):=2\lambda \rho _0\int d\mathbf{y}\, \psi ^t_\mathbf{x}\big (w_{\ge h}(\mathbf{x}-\mathbf{y})-w(\mathbf{x}-\mathbf{y})\big )\psi ^l_\mathbf{y}. \nonumber \\ \end{aligned}$$

(8.16)

Equation (8.15) can be also rewritten in a convenient form by introducing the auxiliary functional $\tilde{\mathcal {W}}^{(h-1)}(\phi ,\Phi ^1,\Phi ^2,J^\Delta )$:

$$\begin{aligned} e^{-\tilde{\mathcal {W}}^{(h-1)}(\phi ,\Phi ^1,\Phi ^2,J^\Delta )}=e^{|\Lambda |{\mathcal {F}}_{h-1}}\int P^B_{\ge h}(d\psi )e^{-\bar{V}(\psi +\phi )-\int d\mathbf{x}[\Phi ^1_\mathbf{x}F^1_\mathbf{x}(\phi )+\Phi ^2_\mathbf{x}F^2_\mathbf{x}(\psi ,\phi )+ J^\Delta _\mathbf{x}\Delta _h(\mathbf{x})]} \nonumber \\ \end{aligned}$$

(8.17)

with

$$\begin{aligned} F^1_\mathbf{x}(\phi )=\bar{\nu }\sqrt{2\rho _0}\phi ^t_\mathbf{x},\quad F^2_\mathbf{x}(\psi ,\phi )=2\lambda \rho _0 \int d\mathbf{y}\,w(\mathbf{x}-\mathbf{y}) \big [\big (\phi ^t_\mathbf{x}+ \psi ^t_\mathbf{x})\big (\psi ^l_\mathbf{y}+ \phi ^l_\mathbf{y}\big )-\psi ^t_\mathbf{x}\psi ^l_\mathbf{y}\big ],\nonumber \\ \end{aligned}$$

(8.18)

in terms of which (8.15) takes the form:

$$\begin{aligned} 0&= \int d\mathbf{x}\left[ \frac{\delta \tilde{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \phi _{\mathbf{x}}^{l}}\phi _{\mathbf{x}}^{t} -\frac{\delta \tilde{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \phi _{\mathbf{x}}^{t}} \left( \phi _{\mathbf{x}}^{l}+\sqrt{2\rho _{0}}\right) \right. \\&\left. +\,\frac{\delta \tilde{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \Phi ^1_\mathbf{x}}+\frac{\delta \tilde{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \Phi ^2_\mathbf{x}} -\frac{\delta \tilde{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta J^\Delta _\mathbf{x}}\right] \nonumber \end{aligned}$$

(8.19)

and $(\phi ,{\mathbf {0}})$ is a shorthand for $(\phi ,0,0,0)$. At this point, we can obtain infinitely many identities among the kernels of ${\mathcal {W}}^{(h-1)}$, known as global WIs, by further deriving (8.15) or (8.19) w.r.t. $\phi ^{l},\phi ^t$, and then taking $\phi \equiv 0$. The “formal” global WIs (discussed e.g. in [15, 39] in the framework of dimensional regularization) are those obtained by neglecting the effect of the cutoff, i.e., by neglecting $\langle \Delta _h(\mathbf{x})\rangle _h^\phi$ in the second line of (8.15).

A few global WIs that we are interested in are those obtained by: (1) deriving w.r.t. $\phi ^t_\mathbf{x},\phi ^l_\mathbf{y}$, then integrating w.r.t. $\mathbf{y}$; (2) deriving w.r.t. $\phi ^t_\mathbf{x},\phi ^t_\mathbf{y},\phi ^t_\mathbf{z}$ and then integrating w.r.t. $\mathbf{y},\mathbf{z}$; (3) deriving w.r.t. $\phi ^t_\mathbf{x}$ (of course in all these cases we put $\phi \equiv 0$ after the derivation). Their explicit expression is (neglecting for simplicity the issue of the “last integration scale” mentioned in footnote 15, a couple of pages above):

$$\begin{aligned}&Z_{h-1}-2 \gamma ^{2h-{\bar{h}}} \nu _h -2\sqrt{2\rho _0}\gamma ^{h/2}\mu _h =\int d\mathbf{x}\, d\mathbf{y}\frac{\delta ^3 \tilde{\mathcal {W}}^{(h)}({\mathbf {0}})}{\delta J^\Delta _{\mathbf {0}}\delta \psi ^t_\mathbf{x}\delta \psi ^l_\mathbf{y}}, \end{aligned}$$

(8.20)

$$\begin{aligned}&\gamma ^{h/2}\mu _h-4\sqrt{2\rho _0}\gamma ^{h-{\bar{h}}}\lambda _h=\frac{1}{3!}\int d\mathbf{x}\, d\mathbf{y}\, d\mathbf{z}\, \frac{\delta ^4 \tilde{\mathcal {W}}^{(h)}({\mathbf {0}})}{\delta J^\Delta _{\mathbf {0}}\delta \psi ^t_\mathbf{x}\delta \psi ^t_\mathbf{y}\delta \psi ^t_\mathbf{z}}, \end{aligned}$$

(8.21)

$$\begin{aligned}&W^{(h)}_{1,0}+\sqrt{2\rho _0}\left( \bar{\nu }-\hat{W}^{(h)}_{0,2}({\mathbf {0}})\right) =\int d\mathbf{x}\,\frac{\delta ^2 \tilde{\mathcal {W}}^{(h)}({\mathbf {0}})}{\delta J^\Delta _{\mathbf {0}}\delta \psi ^t_\mathbf{x}}. \end{aligned}$$

(8.22)

The first two identities are clearly useful, because they relate the running coupling constants among each other. The last identity can be read as a renormalization condition, which fixes the chemical potential to the “right value”, and is known as the Hugenholtz-Pines identity.

It is easy to check that the correction terms in these identities are “trivial”, in the sense that they vanish in the limit of sharp cutoff function, in which case we can drop all these terms at once.

1.2 Appendix 4.2: Local Ward Identities

The local Ward identities are derived in a way completely analogous to the global ones, with the only difference that the phase factor $\alpha (\mathbf{x})$ appearing in the change of variables $\psi ^\pm _\mathbf{x}\rightarrow e^{\pm i \alpha _\mathbf{x}}\psi ^\pm _\mathbf{x}$ is a non-trivial function of $\mathbf{x}$, and the derivatives w.r.t. $\alpha$ performed in the previous section should be replaced by functional derivatives w.r.t. $\alpha (\mathbf{x})$. When we derive (8.1) w.r.t. $\alpha (\mathbf{x})$ we produce a number of terms that are essentially the same as those discussed in the previous section, except for the fact that there is an integration over $\mathbf{x}$ missing; e.g., the analogue of (8.11) is

$$\begin{aligned}&\frac{\delta }{\delta \alpha (\mathbf{x})} \bar{W}(e^{i \alpha }\psi + \phi ) \Big |_{\alpha (\mathbf{x})\equiv 0}\nonumber \\&\quad = -i \left[ \frac{\delta \bar{W}(\psi +\phi )}{\delta \phi ^+_\mathbf{x}}\big ( \phi ^+_\mathbf{x}+ \sqrt{\rho _0}\big ) - \frac{\delta \bar{W}(\psi +\phi )}{\delta \phi ^-_\mathbf{x}}\big ( \phi ^-_\mathbf{x}+ \sqrt{\rho _0}\big )\right] , \end{aligned}$$

(8.23)

etc. In addition to these terms (i.e., the “local” analogues of those of the previous section), there is an extra contribution coming from the measure $P^0_{\ge h}(d\psi )$, which is not invariant under a local gauge transformation (while it was invariant under a global one). The gaussian weight entering the definition of $P^0_{\ge h}(d\psi )$ has the form

$$\begin{aligned} \exp \left\{ -\int \frac{d\mathbf{k}}{(2\pi )^3}\hat{\chi }_{\ge h}^{-1}(\mathbf{k})\hat{\psi }_{\mathbf{k}}^{+}(-ik_0+|{\vec {k}}|^2)\hat{\psi }^-_\mathbf{k}\right\} =: \exp \left\{ -\int d\mathbf{x}\, \psi ^+_\mathbf{x}(D_{\ge h}\psi ^-_{\cdot })_\mathbf{x}\right\} \quad \end{aligned}$$

(8.24)

where the pseudo-differential operator $D_{\ge h}$ is defined here for the first time. Taking the functional derivative of the expression in braces, we find, after some algebra:

$$\begin{aligned}&-\frac{\delta }{\delta \alpha (\mathbf{x})}\int d\mathbf{x}' \, e^{+i\alpha ({\mathbf{x}'})}\psi _{\mathbf{x}}^{+}\Big (D_{\ge h}(e^{-i\alpha (\cdot )}\psi _{\cdot }^{-})\Big )_{\!\mathbf{x}'}\,\Big |_{\alpha (\mathbf{x})\equiv 0}\\&\qquad \qquad = -i \Big [\partial _{0}(\psi ^+_\mathbf{x}\psi ^-_\mathbf{x})+\Delta (\psi ^+_\mathbf{x}\psi ^-_\mathbf{x})-2\vec \partial (\psi ^+_\mathbf{x}\vec \partial \psi ^-_\mathbf{x})\Big ]-\delta T_h(\mathbf{x}),\nonumber \end{aligned}$$

(8.25)

where $\partial _0=\partial _{x_0}$, $\vec \partial =(\partial _{x_1},\partial _{x_2})$, and

$$\begin{aligned} \delta T_h(\mathbf{x})= i \int \frac{d\mathbf{k}\, d\mathbf{p}}{(2\pi )^6} \,e^{i\mathbf{p}\mathbf{x}}\hat{\psi }_{\mathbf{k}+\mathbf{p}}^{+} C_h(\mathbf{k},\mathbf{p}) \hat{\psi }^-_\mathbf{k}, \end{aligned}$$

(8.26)

with

$$\begin{aligned} C_h(\mathbf{k},\mathbf{p}) := \big (\hat{\chi }_{\ge h}^{-1}(\mathbf{k})-1\big ) (-i k_{0} + |{\vec {k}}|^2) - \big (\hat{\chi }_{\ge h}^{-1}(\mathbf{k}+\mathbf{p})-1\big ) (-i(k_{0}+p_{0}) + |{\vec {k}}+{\vec {p}}|^2)\nonumber \\ \end{aligned}$$

(8.27)

The equations above can be rewritten in terms of the fields $\psi ^{l},\psi ^t$, in terms of which we find

$$\begin{aligned}&-\frac{\delta }{\delta \alpha (\mathbf{x})}\int d\mathbf{x}' \, e^{+i\alpha ({\mathbf{x}'})}\psi _{\mathbf{x}}^{+}\Big (D_{\ge h}(e^{-i\alpha (\cdot )}\psi _{\cdot }^{-})\Big )_{\!\mathbf{x}'}\,\Big |_{\alpha (\mathbf{x})\equiv 0} =-i(\partial _0 j_{0,\mathbf{x}}+\vec \partial \, \vec j_\mathbf{x})-\delta T(\mathbf{x}), \end{aligned}$$

(8.28)

with

$$\begin{aligned} j_{0, \mathbf{x}}&= \,\frac{1}{2}\left[(\psi _{\mathbf{x}}^{l})^2+(\psi _{\mathbf{x}}^{t})^2\right],\end{aligned}$$

(8.29)

$$\begin{aligned} \vec j_\mathbf{x}&= i\psi ^l_\mathbf{x}\vec \partial \psi ^t_\mathbf{x}-i\psi ^t_\mathbf{x}\vec \partial \psi ^l_\mathbf{x}\end{aligned}$$

(8.30)

and

$$\begin{aligned} \delta T_h(\mathbf{x})&= \int \frac{d\mathbf{k}\, d\mathbf{p}}{(2\pi )^6} \,e^{i\mathbf{p}\mathbf{x}}\left( \hat{\chi }_{\ge h}^{-1}(\mathbf{k})-1\right) \Big [k_0(\hat{\psi }^l_{-\mathbf{k}-\mathbf{p}}\hat{\psi }^l_\mathbf{k}+ \hat{\psi }^t_{-\mathbf{k}-\mathbf{p}}\hat{\psi }^t_\mathbf{k})\\&\quad +|{\vec {k}}|^2 (\hat{\psi }^l_{-\mathbf{k}-\mathbf{p}}\hat{\psi }^t_\mathbf{k}- \hat{\psi }^t_{-\mathbf{k}-\mathbf{p}}\hat{\psi }^l_\mathbf{k})\Big ].\nonumber \end{aligned}$$

(8.31)

After having performed the functional derivative w.r.t. $\alpha (\mathbf{x})$ and having re-expressed everything in terms of the $\psi ^l,\psi ^t$ fields, we finally arrive at the analogue of (8.15), which reads

$$\begin{aligned}&-i \left\langle \partial _0 j_{0,\mathbf{x}}+\vec \partial \,\vec j_\mathbf{x}\right\rangle ^\phi _h =\frac{\delta {\mathcal {W}}^{(h-1)}(\phi )}{\delta \phi _{\mathbf{x}}^{l}}\phi _{\mathbf{x}}^{t} -\frac{\delta {\mathcal {W}}^{(h-1)}(\phi )}{\delta \phi _{\mathbf{x}}^{t}} \left( \phi _{\mathbf{x}}^{l}+\sqrt{2\rho _{0}}\right) +\bar{\nu }\sqrt{2\rho _0} \langle \phi ^t_\mathbf{x}\rangle _h^\phi \\&+ 2\lambda \rho _0 \int d\mathbf{y}\, w(\mathbf{x}-\mathbf{y})\left\langle \left[ \big (\phi ^t_\mathbf{x}+ \psi ^t_\mathbf{x})\big (\psi ^l_\mathbf{y}+ \phi ^l_\mathbf{y}\big )-\psi ^t_\mathbf{x}\psi ^l_\mathbf{y}\right] \right\rangle _h^\phi -\langle \Delta _h(\mathbf{x})\rangle _h^\phi +\langle \delta T_h(\mathbf{x})\rangle _h^\phi .\nonumber \end{aligned}$$

(8.32)

If desired, this equation can be put in a form similar to (8.19). It is enough to introduce the auxiliary potential

$$\begin{aligned} e^{-\bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {J}},\vec \Phi ,J^\Delta ,J^{\delta T})}=e^{|\Lambda |{\mathcal {F}}_{h-1}}\int P^B_{\ge h}(d\psi )e^{-\bar{V}(\psi +\phi )-({\mathbf {J}},{\mathbf {J}})-(\vec \Phi , \vec {F})- (J^\Delta ,\Delta _h)-(J^{\delta T},\delta T)]}\nonumber \\ \end{aligned}$$

(8.33)

where: ${\mathbf {J}}=(J_0,J_1,J_2)=(J_0,\vec J)$, $\vec \Phi =(\Phi ^1,\Phi ^2)$, and $({\mathbf {J}},{\mathbf {J}})=\int d\mathbf{x}(J_{0,\mathbf{x}}j_{0,\mathbf{x}}+\vec J_\mathbf{x}\,\vec j_{\mathbf{x}})$, $(\vec \Phi , \vec {F})=\sum _{i=1}^2\int d\mathbf{x}\Phi ^i_\mathbf{x}F^i_\mathbf{x}$, etc. Using the auxiliary potential (8.33), Eq.(8.32) takes the form:

$$\begin{aligned}&-i\,\partial _0\, \frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi , {\mathbf {0}})}{\delta J_{0,\mathbf{x}}}-i\,\vec \partial \, \frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi , {\mathbf {0}})}{\delta \vec J_{\mathbf{x}}} \nonumber \\&=\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \phi _{\mathbf{x}}^{l}}\phi _{\mathbf{x}}^{t} -\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \phi _{\mathbf{x}}^{t}} \left( \phi _{\mathbf{x}}^{l}+\sqrt{2\rho _{0}}\right) \\&+\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \Phi ^1_\mathbf{x}}+\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta \Phi ^2_\mathbf{x}}-\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta J^\Delta _\mathbf{x}} +\frac{\delta \bar{\mathcal {W}}^{(h-1)}(\phi ,{\mathbf {0}})}{\delta J^{\delta T}_\mathbf{x}}. \nonumber \end{aligned}$$

(8.34)

At this point, we can obtain infinitely many identities among the kernels of ${\mathcal {W}}^{(h-1)}$, known as local WIs, by further deriving this identity w.r.t. $\phi ^{l,t}$, and then taking $\phi \equiv 0$. The “formal” local WIs (discussed e.g. in [15, 39] in the framework of dimensional regularization) are those obtained by neglecting the effect of the cutoffs, i.e., by dropping the terms $\langle \Delta _h(\mathbf{x})\rangle _h^\phi$ and $\langle \delta T_h(\mathbf{x})\rangle _h^\phi$.

Two local WIs we are interested in are those obtained by deriving w.r.t. $\phi ^l$, or w.r.t. $\phi ^t$, and then taking the Fourier transform at $\mathbf{p}=(p_0,\vec {0})$. Their explicit expression in momentum space is (neglecting for simplicity the issue of the “last integration scale”):

$$\begin{aligned} p_0 \hat{W}^{(h)}_{1,0;J_0}(p_0,\vec {0})&= -\sqrt{2\rho _0}\hat{W}^{(h)}_{1,1}(p_0,\vec {0}) + W^{(h)}_{0,1} +\hat{W}^{(h)}_{1,0;J^\Delta }(p_0,\vec {0})-\hat{W}^{(h)}_{1,0;J^{\delta T}}(p_0,\vec {0}), \end{aligned}$$

(8.35)

$$\begin{aligned} p_0 \hat{W}^{(h)}_{0,1;J_0}(p_0,\vec {0})&= 2\sqrt{2\rho _0}\hat{W}^{(h)}_{0,2}(p_0,\vec {0}) - W^{(h)}_{1,0} +\hat{W}^{(h)}_{0,1;J^\Delta }(p_0,\vec {0})-\hat{W}^{(h)}_{0,1;J^{\delta T}}(p_0,\vec {0}) , \end{aligned}$$

(8.36)

where $W^{(h)}_{1,0;J_0}(\mathbf{x},\mathbf{y})$ is the kernel of $J_{0,\mathbf{x}}\psi ^l_\mathbf{y}$ in $\bar{\mathcal {W}}^{(h)}(\phi ,J_0,{\mathbf {0}})$, and $\hat{W}^{(h)}_{1,0;J_0}(\mathbf{p})=\int d\mathbf{x}e^{i\mathbf{p}\mathbf{x}}$ $W^{(h)}_{1,0;J_0}(\mathbf{x},{\mathbf {0}})$ (and similarly for $\hat{W}^{(h)}_{1,0;J^\Delta }(\mathbf{p})$, etc). Eqs.(8.35)–(8.36) are the analogues of [39, (3.11)-(3.12)]. If we divide (8.35) by $p_0$ and then take the limit $p_0\rightarrow 0$ we find:

$$\begin{aligned} Z_{h-1}^{J_0}=\sqrt{2\rho _0}(E_{h-1}-1)+\partial _{p_0}\hat{W}^{(h)}_{1,0;J^\Delta }({\mathbf {0}})-\partial _{p_0}\hat{W}^{(h)}_{1,0;J^{\delta T}}({\mathbf {0}}), \end{aligned}$$

(8.37)

where $Z_{h-1}^{J_0}:=\hat{W}^{(h)}_{1,0;J_0}({\mathbf {0}})$, and the name is justified by the fact that the Feynman diagram expansion for $Z_h^{J_0}$ has the same structure as that for $Z_h$. In particular, inspection of perturbation theory shows that

$$\begin{aligned} Z_h^{J_0}=\frac{Z_h - Z_{\bar{h}}}{\lambda \hat{v}(\vec {0})\sqrt{2\rho _0}}\big (1+O(\gamma ^{h-{\bar{h}}})\big ), \end{aligned}$$

(8.38)

where the error terms in parentheses come from the irrelevant terms on scale ${\bar{h}}$. In a similar way, if we divide (8.36) by $p_0^2$ and then take the limit $p_0\rightarrow 0$ we find, defining $E_{h-1}^{J_0}:= -\partial _{p_0}\hat{W}^{(h)}_{0,1;J_0}({\mathbf {0}})$:

$$\begin{aligned} -2E_{h-1}^{J_0}=2\sqrt{2\rho _0}B_{h-1}+\partial ^2_{p_0}\hat{W}^{(h)}_{0,1;J^\Delta }({\mathbf {0}})-\partial ^2_{p_0}\hat{W}^{(h)}_{0,1;J^{\delta T}}({\mathbf {0}}), \end{aligned}$$

(8.39)

where

$$\begin{aligned} E_h^{J_0}=\frac{E_h - 1}{\lambda \hat{v}(\vec {0})\sqrt{2\rho _0}}\big (1+O(\gamma ^{h-{\bar{h}}})\big ). \end{aligned}$$

(8.40)

Contrary to the correction terms of the global Ward Identities, the corrections in (8.37), (8.39) are not “trivial”, i.e., they do not vanish in the sharp cutoff limit. On the contrary, they give a finite (cutoff-dependent) contribution to the beta function, which shows up as an “anomaly” already at the level of the one-loop beta function, as discussed in Sect. 3.3.4.

1.3 Appendix 4.3: Comparison Between ${\mathcal {W}}^{(h-1)}$ and ${\mathcal {V}}^{(h-1)}$

In order to establish the exact relation between ${\mathcal {W}}^{(h-1)}$ and ${\mathcal {V}}^{(h-1)}$, we compute the r.h.s. of (8.1) via a multiscale integration analogous to the one used in the bulk of the paper for the computation of ${\mathcal {V}}^{(h-1)}$. The integration of the ultraviolet fields on scales $>{\bar{h}}$, as well as the integration of the field $\tilde{\psi }^{({\bar{h}})}$ (see (3.40)), is identical to the one discussed in Sect. 3.2 and at the beginning of Sect. 3.3, after which we can rewrite (8.1) as

$$\begin{aligned} e^{-|\Lambda |{\mathcal {F}}_{h-1}-{\mathcal {W}}^{(h-1)}(\phi )}=e^{-|\Lambda |\sum _{k\ge {\bar{h}}}F_k}\int P_{[h,{\bar{h}}]}(d\psi )e^{-{\mathcal {V}}^{({\bar{h}})}(\psi +\phi )}, \end{aligned}$$

(8.41)

where $P_{[h,{\bar{h}}]}(d\psi )$ is the same as the gaussian measure $P_{\le {\bar{h}}}(d\psi )$ in (3.40), modulo the presence of an infrared cutoff on scale $h$ in the corresponding propagator (i.e., while the cutoff function appearing in the propagator of $P_{\le {\bar{h}}}(d\psi )$ is $\chi _{{\bar{h}}}(\mathbf{k})$, the one in the propagator of $P_{[h,{\bar{h}}]}(d\psi )$ is $\chi _{{\bar{h}}}(\mathbf{k})-\chi _{h-1}(\mathbf{k})$). Moreover, using the same convention of Sect. 3.3.2, ${\mathcal {V}}^{(\bar{h})}$ coincides with the function $\bar{V}^{(\bar{h})}$ introduced after (3.40). At this point, we start dressing the gaussian measure in (8.41), in the same way as in Sect. 3.3.2. Let us describe the first integration step explicitly. Using the notations introduced in (3.64) and following equations, we rewrite the r.h.s. of (8.41) as

$$\begin{aligned} e^{-|\Lambda |\sum _{k\ge {\bar{h}}}F_k+{\mathcal {L}}_Q{\mathcal {V}}^{({\bar{h}})}(\phi )} \int P_{[h,{\bar{h}}]}(d\psi )e^{-{\mathcal {L}}_Q{\mathcal {V}}^{({\bar{h}})}(\psi )-\widehat{\mathcal {V}}^{({\bar{h}})}(\psi +\phi )-\big (\psi +\phi ,M_Q^{({\bar{h}})}\phi \big )}, \end{aligned}$$

(8.42)

where $\widehat{\mathcal {V}}^{({\bar{h}})}$ is a shorthand for ${\mathcal {L}}_C{\mathcal {V}}^{({\bar{h}})}+{\mathcal {R}}{\mathcal {V}}^{({\bar{h}})}$. We now combine ${\mathcal {L}}_Q{\mathcal {V}}^{({\bar{h}})}(\psi )$ with the gaussian measure, as in (3.66), and then use the addition principle to rewrite the dressed measure as a product of a measure supported on scale ${\bar{h}}$ and a measure supported on smaller scales, as in (3.72):

$$\begin{aligned} (8.41)&=e^{-|\Lambda |(\sum _{k\ge {\bar{h}}}F_k+t_{{\bar{h}}})+{\mathcal {L}}_Q{\mathcal {V}}^{({\bar{h}})}(\phi )}\int P_{[h,{\bar{h}}-1]}(d\psi )\\&\quad \cdot \int \tilde{P}_{{\bar{h}}}(d\psi ^{({\bar{h}})}) e^{-\widehat{\mathcal {V}}^{({\bar{h}})}(\psi ^{({\bar{h}})}+\psi +\phi )-\big (\psi ^{({\bar{h}})}+\psi +\phi ,M_Q^{({\bar{h}})}\phi \big )}.\nonumber \end{aligned}$$

(8.43)

At this point, we integrate the field on scale ${\bar{h}}$ and define:

$$\begin{aligned} |\Lambda | {\tilde{F}}_{{\bar{h}}}&+\tilde{S}_{\bar{h}}(\phi )+{\mathcal {V}}^{({\bar{h}}-1)}(\psi ')+{\mathcal {B}}^{({\bar{h}}-1)}(\psi ',\phi )\end{aligned}$$

(8.44)

$$\begin{aligned}&\qquad = -\log \int \tilde{P}_{h}(d\psi ^{(h)}) e^{-\widehat{\mathcal {V}}^{({\bar{h}})}(\psi ^{({\bar{h}})}+\psi ')-\big (\psi ^{({\bar{h}})}+\psi ',M_Q^{({\bar{h}})}\phi \big )}. \end{aligned}$$

(8.45)

where, denoting by $\hat{\phi }_\mathbf{k}$ the two-component column vector with components $\hat{\phi }_\mathbf{k}^l$ and $\hat{\phi }_\mathbf{k}^t$,

$$\begin{aligned} \tilde{S}_{\bar{h}}(\phi )=-\frac{1}{2}\int \frac{d\mathbf{k}}{(2\pi )^3}\hat{\phi }^T_{-\mathbf{k}}\big [\hat{M}_Q^{({\bar{h}})}(\mathbf{k})\big ]^T\hat{\tilde{g}}^{({\bar{h}})}(\mathbf{k})\hat{M}_Q^{({\bar{h}})}(\mathbf{k})\hat{\phi }_\mathbf{k}\equiv -\frac{1}{2}\left( \phi , M_Q^{({\bar{h}}),T}{\tilde{g}}^{({\bar{h}})}M_Q^{({\bar{h}})}\phi \right) .\nonumber \\ \end{aligned}$$

(8.46)

We now set $F_{{\bar{h}}-1}=t_{\bar{h}}+\tilde{F}_{\bar{h}}$ and $S^{({\bar{h}}-1)}={\mathcal {L}}_Q{\mathcal {V}}^{({\bar{h}})}-\tilde{S}_{\bar{h}}$, and then we iterate the same procedure. After the integration of the fields on scales $\ge k+1$ we rewrite (8.1) as

$$\begin{aligned} e^{-|\Lambda |\sum _{k'\ge k}F_{k'}+ S^{(k)}(\phi )}\int P_{[h,k]}(d\psi )e^{-{\mathcal {V}}^{(k)}(\psi +\phi )-{\mathcal {B}}^{(k)}(\psi +\phi ,\phi )}, \end{aligned}$$

(8.47)

where one can inductively prove that, for $k<{\bar{h}}$,

$$\begin{aligned}&S^{(k)}(\phi )=\!\!\sum _{k'=k+1}^{{\bar{h}}}\!\Big [{\mathcal {L}}_Q{\mathcal {V}}^{(k')}(\phi )\!+\!\frac{1}{2}\big (\phi ,Q^{(k'),T}\tilde{g}^{(k')}Q^{(k')}\phi \big )-\!\frac{1}{2}\big (\phi ,G^{(k'+1),T}M_Q^{(k')}G^{(k'+1)}\phi \big )\!\Big ],\end{aligned}$$

(8.48)

$$\begin{aligned}&{\mathcal {B}}^{(k)}(\psi ,\phi )\!=\!\big (\psi ,Q^{(k+1)}\phi \big ) \!+\!\!\sum _{n\ge 1}\int \! d\mathbf{x}_1\cdots d\mathbf{x}_n \left[ \prod _{i=1}^n \big ( G^{(k+1)}*\phi \big )_{\mathbf{x}_i}\!\right] \frac{\partial ^n}{\partial \psi _{\mathbf{x}_1}\cdots \partial \psi _{\mathbf{x}_n}}{\mathcal {V}}^{(k)}(\psi ), \end{aligned}$$

(8.49)

and the vectorial nature of $\psi$ (i.e., the fact that $\psi$ has two components, labelled $l$ and $t$) is implicitly understood. Moreover, the functions $Q^{(k)}$ and $G^{(k)}$, $k\le {\bar{h}}+1$, are defined by the iterative relations

$$\begin{aligned} Q^{(k)}=Q^{(k+1)}+M_Q^{(k)}+M_Q^{(k)}G^{(k+1)},\qquad G^{(k)}=G^{(k+1)}+\tilde{g}^{(k)}Q^{(k)}, \end{aligned}$$

(8.50)

with $Q^{({\bar{h}}+1)}=G^{({\bar{h}}+1)}=0$.

The iteration goes on in the same fashion until we reach scale $h$, where a small difference from the previous scheme should be taken into account: in fact, by proceeding as described above, one finds that the dressed propagator on the last scale, rather than being equal to $\tilde{g}^{(h)}$, it is equal to

$$\begin{aligned} \tilde{\mathfrak g}^{(h)}(\mathbf{x})= \int \frac{d\mathbf{k}}{(2\pi )^3}\, {\tilde{f}}_{h}(\mathbf{k})\,\frac{\, e^{-i\mathbf{k}\cdot \mathbf{x}}}{{\mathcal {D}}_{h-1}(\mathbf{k})}\left( \begin{array}{c@{\quad }c} {\tilde{A}}_{h-1}'(\mathbf{k})\, |{\vec {k}}|^{2} + {\tilde{B}}_{h-1}'(\mathbf{k})\, k_0^2 &{} {\tilde{E}}_{h-1}'(\mathbf{k})\, k_{0}\\ -\tilde{E}_{h-1}'(\mathbf{k})\, k_{0} &{} {\tilde{Z}}_{h-1}'(\mathbf{k}) \end{array}\right) \nonumber \\ \end{aligned}$$

(8.51)

where ${\tilde{f}}(\mathbf{k})=\chi _h(\mathbf{k})-\chi _{h-1}(\mathbf{k})$, as usual, and

$$\begin{aligned} {\tilde{A}}_{h-1}'(\mathbf{k}) = {\tilde{A}}_h(\mathbf{k}) + a_h \tilde{f}_h(\mathbf{k}),&{\tilde{B}}_{h-1}(\mathbf{k}) = {\tilde{B}}_h (\mathbf{k})+ b_h {\tilde{f}}_h(\mathbf{k}) , \nonumber \\ {\tilde{E}}_{h-1}(\mathbf{k}) = {\tilde{E}}_h (\mathbf{k}) + e_h \tilde{f}_h(\mathbf{k}) ,&{\tilde{Z}}_{h-1}(\mathbf{k}) = {\tilde{Z}}_h(\mathbf{k}) + z_h {\tilde{f}}_h(\mathbf{k}). \end{aligned}$$

(8.52)

After the integration of the last scale we finally find

$$\begin{aligned} (8.1)=e^{-|\Lambda |(\sum _{k'\ge h}F_{k'}+\tilde{F}_{h-1}) +\tilde{S}^{(h-1)}(\phi )-\tilde{\mathcal {V}}^{(h-1)}(\phi )-\tilde{\mathcal {B}}^{(h-1)}(\phi ,\phi )}\equiv e^{-|\Lambda |{\mathcal {F}}_{h-1}-{\mathcal {W}}^{(h-1)}(\phi )},\nonumber \\ \end{aligned}$$

(8.53)

where the tildes on the functions at exponent recall the fact that these functions are defined in the same fashion as their analogues without tilde, with the only difference that the single-scale propagator on the last scale, $\tilde{g}^{(h)}$, wherever it enters the definition of these objects, should be replaced by $\tilde{\mathfrak g}^{(h)}$.

Equation (8.53) provides us the desired relation between ${\mathcal {W}}^{(h-1)}$ and ${\mathcal {V}}^{(h-1)}$. It shows that the local parts of the kernels of ${\mathcal {W}}^{(h-1)}$ (in the sense of the values of their Fourier transforms at zero external momenta, as well as the zero momenta values of their derivatives w.r.t. $\mathbf{k}$), are related in a very simple fashion with the corresponding local parts of the kernels of ${\mathcal {V}}^{(h-1)}$, simply because the local part of the kernels of $\tilde{\mathcal {B}}^{(h-1)}(\phi ,\phi )$ is equal to $2\sum _{k=h}^{\bar{h}}{\mathcal {L}}_Q{\mathcal {V}}^{(k)}(\phi )$, due to the compact support properties of $\tilde{g}^{(k)}$ and of $G^{(k)}$, and similarly the local part of $\tilde{S}^{(h-1)}$ is equal to $\sum _{k=h}^{\bar{h}}{\mathcal {L}}_Q{\mathcal {V}}^{(k)}$. Therefore,

$$\begin{aligned} {\mathcal {L}}{\mathcal {W}}^{(h-1)}(\phi )= {\mathcal {L}}\tilde{\mathcal {V}}^{(h-1)}(\phi )+\sum _{k=h}^{{\bar{h}}}{\mathcal {L}}_Q{\mathcal {V}}^{(k)}, \end{aligned}$$

(8.54)

which induces a simple, explicit, connection between the actual renormalization and running coupling constants of the model, introduced in Sect. 3.3.2, and ${\mathcal {L}}{\mathcal {W}}^{(h-1)}(\phi )$.

Appendix 5: Verification of Ward Identities at Lowest Order

In this section, we verify the validity of some of the global and local Ward Identities among the running coupling and the renormalization constants, at lowest non trivial order in perturbation theory. In particular, we shall compute the effect of the infrared cutoff and discuss its role in the different identities worked out below.

1.1 Appendix 5.1: Global Ward Identities

Let us verify the validity of (8.20) at lowest non trivial order in $\lambda$ and/or in $\gamma ^{h-{\bar{h}}}$, in the region $h^*\le h\le {\bar{h}}$. If $W^{(h)}_{1,1;J^\Delta }(\mathbf{x},\mathbf{y};\mathbf{0})$ is the kernel of $J^\Delta _{\mathbf{0}}\phi ^t_\mathbf{x}\phi ^l_\mathbf{y}$ in ${\tilde{{\mathcal {W}}}}^{(h)}(\phi ,J^\Delta , {\mathbf {0}})$, and

$$\begin{aligned} \hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{k},\mathbf{p})=\int d\mathbf{x}\, d\mathbf{y}\, e^{-i\mathbf{k}\mathbf{x}+i(\mathbf{k}+\mathbf{p})\mathbf{y}}W^{(h)}_{1,1;J^D}(\mathbf{x}, \mathbf{y};{\mathbf {0}}), \end{aligned}$$

(9.1)

we can rewrite (8.20) as

$$\begin{aligned} Z_{h-1}-2 \gamma ^{2h-{\bar{h}}} \nu _h -2\sqrt{2\rho _0}\gamma ^{h/2}\mu _h =\hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{0}, \mathbf{0}). \end{aligned}$$

(9.2)

Using the beta function Eqs. (3.77)–(3.80), the l.h.s. can be rewritten as

$$\begin{aligned} Z_{\bar{h}-1}-2 \gamma ^{{\bar{h}}} \nu _{\bar{h}}-2\sqrt{2\rho _0}\gamma ^{{\bar{h}}/2}\mu _{\bar{h}}+\sum _{k=h+1}^{\bar{h}}\Big ( \beta ^Z_k-2\gamma ^{2k-{\bar{h}}}\beta ^\nu _k-2\sqrt{2\rho _0}\gamma ^{k/2}\beta ^\mu _k\Big ). \end{aligned}$$

(9.3)

Now, using the explicit expressions of $Z_{\bar{h}-1}, \nu _{\bar{h}}, \mu _{\bar{h}}$, one can check that the combination $Z_{\bar{h}-1}-2 \gamma ^{{\bar{h}}} \nu _{\bar{h}}-2\sqrt{2\rho _0}\gamma ^{{\bar{h}}/2}\mu _{\bar{h}}$ is zero at lowest order (i.e., at the order $\lambda$, as well as at the order $\bar{\nu }$) and, therefore, it is (at most) of the order $O(\lambda ^2|{\bar{h}}|)$. Moreover, using the explicit expression of the beta functions for $Z_h$, $\nu _h$ and $\mu _h$, see (3.82), (3.83), (3.89), as well as the replacements

$$\begin{aligned} Z_{h} \rightarrow 2\sqrt{2\rho _0} \gamma ^{h/2}\mu _{h},\qquad \lambda _h \rightarrow \frac{1}{4\sqrt{2\rho _0}} \gamma ^{{\bar{h}}-h/2} \mu _h\,, \end{aligned}$$

(9.4)

induced by the Ward Identities (8.20)–(8.21) (which, once inserted in the expressions (3.82), (3.83), (3.89) of the one-loop beta function, induce errors of higher order in $\lambda$ and/or in $\gamma ^{h-{\bar{h}}}$, as one can prove inductively in $h$), we can rewrite, for $h^*\le h\le {\bar{h}}$,

$$\begin{aligned}&\sum _{k=h+1}^{\bar{h}}\Big ( \beta ^Z_k-2\gamma ^{2k-{\bar{h}}}\beta ^\nu _k-2\sqrt{2\rho _0}\gamma ^{k/2}\beta ^\mu _k\Big )= \sum _{k=h+1}^{\bar{h}}\left( -\frac{2\mu _k^2}{A_k C_k}\beta _0^{(2)}\right. \nonumber \\&\left. \qquad -\frac{2\gamma ^k}{A_k C_k}\frac{1}{8\rho _0}\left( \beta _0^{(1)}-2\beta _0^{(1,\chi )}\right) +\frac{2\mu _k^2}{A_k C_k}\left( \beta _0^{(2)}+2\beta _0^{(2,\chi )}\right) \right) \end{aligned}$$

(9.5)

modulo higher order correction terms in $\lambda$ and/or in $\gamma ^{h-{\bar{h}}}$ (in deriving the expression of the first term in the second line we also used the fact that $C_kZ_k=1$, up to higher order corrections). Now, the sum over $k$ of $-\frac{2\gamma ^k}{A_k C_k}\frac{1}{8\rho _0}(\beta _0^{(1)}-2\beta _0^{(1,\chi )})$ is of the order $\lambda ^2$, which is subdominant with respect to the other two terms, whose sum over $k$ gives (using the fact that $\mu _k=\gamma ^{({\bar{h}}-k)/2} \mu _{\bar{h}}$, up to higher order corrections)

$$\begin{aligned} \frac{\gamma }{\gamma -1}\frac{4\mu _{h+1}^2}{A_{h+1} C_{h+1}}\beta _0^{(2,\chi )}. \end{aligned}$$

(9.6)

We now want to show that this expression is equal to $\hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{0}, \mathbf{0})$, modulo higher order corrections. In fact, the lowest order contribution to $\hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{0}, \mathbf{0})$ is given by the sum of the diagrams in Fig. 23, with at least one propagator at scale $h$. After the same considerations made for the calculation of the beta function for $\mu _{h}$ (see Appendix 3.3) we find that, at lowest order,

$$\begin{aligned}&\hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{0}, \mathbf{0}) =\,\, 8 \lambda \rho _0 \hat{v} (\vec {0}) \frac{\mu _{h+1}^2}{Z_{h+1}}\frac{1}{A_{h+1} C_{h+1}}\nonumber \\&\quad \times \int \frac{d^3\mathbf{k}}{(2\pi )^3} \left( \frac{1}{\sum _{k\ge 0}{\mathfrak {f}}_k(|\mathbf{k}|)} -1 \right) {\mathfrak {f}}_0(|\mathbf{k}|) \frac{{\mathfrak {f}}_0^2(|\mathbf{k}|) +3 {\mathfrak {f}}_0(|\mathbf{k}|) {\mathfrak {f}}_{1}(|\mathbf{k}|) +3 {\mathfrak {f}}^2_{1}(|\mathbf{k}|) }{|\mathbf{k}|^4}. \end{aligned}$$

(9.7)

Note that, for $j\ge 0$,

$$\begin{aligned} \left( \frac{1}{\sum _{k\ge 0}{\mathfrak {f}}_k(|\mathbf{k}|)} -1 \right) {\mathfrak {f}}_j(|\mathbf{k}|) = u_0(|\mathbf{k}|)\delta _{0,j} \end{aligned}$$

(9.8)

where

$$\begin{aligned} u_0(|\mathbf{k}|):= {\left\{ \begin{array}{ll} 1 - {\mathfrak {f}}_0(|\mathbf{k}|), &{}\mathrm{if}\ \gamma ^{-1} \le |\mathbf{k}| \le 0 \\ 0\;, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(9.9)

Note that, if $\gamma ^{-1} \le |\mathbf{k}|< 1$, then ${\mathfrak {f}}_1(|\mathbf{k}|)=0$. Therefore,

$$\begin{aligned} \hat{W}^{(h)}_{1,1;J^\Delta }(\mathbf{0}, \mathbf{0})&= 8 \lambda \rho _0 \hat{v} (\vec {0}) \frac{\mu _{h+1}^2}{Z_{h+1}} \frac{1}{A_{h+1} C_{h+1}} \frac{1}{2\pi ^2} \int \limits _{\gamma ^{-1}}^1 \frac{d\rho }{\rho ^2}\,(1 - {\mathfrak {f}}_0(\rho )){\mathfrak {f}}^2_0(\rho ) \nonumber \\&= 4\,\mu _{h+1}^2 \frac{1}{A_{h+1} C_{h+1}}\, \frac{\gamma }{2\pi ^2} \int \limits _{1}^\gamma \frac{d\rho }{\rho ^2}\,\chi (\rho ) (1 - \chi (\rho ))^2 \nonumber \\&= 4\,\mu _{h+1}^2 \frac{1}{A_{h+1} C_{h+1}} \frac{\gamma }{\gamma -1}\, \beta _0^{(2,\chi )}, \end{aligned}$$

(9.10)

where we used that $Z_h=2 \lambda \rho _0 \hat{v} (\vec {0})$, up to higher order corrections.

Fig. 23

Correction terms to the formal GWI relating $\mu _h$ and $Z_h$, see (8.20). The triangular vertex with the external zigzag line represents $J^\Delta \Delta _h(\mathbf{x})$, see (8.16) and (8.17)

A similar discussion can be repeated for proving the validity of (8.21), but we will not belabor the details here.

1.2 Appendix 5.2: Local WI Relating $E_h$ and $Z_h$

In this section we prove the validity of the local WI (8.37), that is

$$\begin{aligned} Z_{h-2}^{J_0}=\sqrt{2\rho _0}(E_{h-2}-1)+\partial _{p_0}\hat{W}^{(h-1)}_{1,0;J^\Delta }({\mathbf {0}})-\partial _{p_0}\hat{W}^{(h-1)}_{1,0;J^{\delta T}}({\mathbf {0}}), \end{aligned}$$

(9.11)

at lowest non trivial order. Now, using (3.90), we find that at lowest order

$$\begin{aligned} E_{h-2}- 1 = -2 \frac{1}{A_h C_h Z_h} \mu _h^2 \frac{\gamma }{\gamma -1}\beta _0^{(2)}, \end{aligned}$$

(9.12)

while, using (8.38) and (3.89),

$$\begin{aligned} Z_{h-2}^{J_0} = \sqrt{2\rho _0}\, \frac{Z_{h-2} -Z_{\bar{h}}}{ Z_{\bar{h}}} = - 2 \sqrt{2\rho _0} \frac{1}{A_h C_h Z_{\bar{h}}} \mu _h^2 \frac{\gamma }{\gamma -1} \beta _0^{(2)}, \end{aligned}$$

(9.13)

as can also be checked by an explicit calculation of the second diagram on the first line of Fig. 24. Therefore, at lowest order $Z_{h-2}^{J_0}=\sqrt{2\rho _0}(E_{h-2}-1)$. In fact, it can be checked that the two correction terms in the r.h.s. cancel among each other: at lowest order their values are

$$\begin{aligned} \partial _{p_0}\hat{W}^{(h-1)}_{1,0;J^\Delta }(\mathbf{0})&= - 2 \gamma ^{\frac{h}{2}} \mu _h \frac{2\lambda \rho _0 \hat{v} (\vec {0})E_h}{A_hC_hZ_h}\, \partial _{p_0}\nonumber \\&\quad \int \frac{d^3\mathbf{k}}{(2\pi )^3}\, \big (\hat{\chi }^{-1}_{\ge h}(\mathbf{k}) -1\big ) \, \frac{{\mathfrak {f}}_{h}(|\mathbf{k}+\mathbf{p}|)}{|\mathbf{k}+\mathbf{p}|^2} \frac{k_0 {\mathfrak {f}}_{h}(|\mathbf{k}|)}{|\mathbf{k}|^2}\Big |_{\mathbf{p}={\mathbf {0}}} \nonumber \\ \partial _{p_0}\hat{W}^{(h-1)}_{1,0;J^{\delta T}}(\mathbf{0})&= -2 \gamma ^{\frac{h}{2}}\mu _h \frac{1}{A_h C_h} \partial _{p_0}\nonumber \\&\quad \int \frac{d^3\mathbf{k}}{(2\pi )^3}\, k_0 \big (\hat{\chi }_{\ge h}^{-1}(\mathbf{k}) -1 \big ) \frac{{\mathfrak {f}}_{h}(|\mathbf{k}+\mathbf{p}|)}{|\mathbf{k}+\mathbf{p}|^2} \frac{{\mathfrak {f}}_{h}(|\mathbf{k}|)}{|\mathbf{k}|^2} \Big |_{\mathbf{p}={\mathbf {0}}}, \end{aligned}$$

(9.14)

which are the same, since $E_h=1$ up to higher order corrections.

Fig. 24

Diagrams involved in the local WI relating $E_h$ and $Z_h$. On the first line the lowest order beta function for $E_h$ and $Z^{J_0}_h$. On the second line, the correction terms coming from the cutoffs. The triangular vertex with the external zigzag line represents $J^\Delta _\mathbf{x}\Delta _h(\mathbf{x})$, see (8.16)–(8.17). The diamond vertex with wiggly external line represents $J_{\mathbf{x}}^{\delta T} \delta T_h(\mathbf{x})$, see (8.31)–(8.33)

1.3 Appendix 5.3: Local WI Relating $B_h$ and $E_h$

In this section we prove the validity of the local WI (8.39), that is

$$\begin{aligned} -2E_{h-2}^{J_0}=2\sqrt{2\rho _0}B_{h-2}+\partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^\Delta }({\mathbf {0}})-\partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^{\delta T}}({\mathbf {0}}), \end{aligned}$$

(9.15)

Let us discuss the various terms involved in this equation separately. Using (3.91) and the fact that $B_{\bar{h}}=0$, we find

$$\begin{aligned} B_{h-2} = 2 \frac{\mu ^2_h}{A_h Z_h} \frac{\gamma }{\gamma -1} \left( \frac{E^2_h}{C_h Z_h} \beta _0^{(2)}+\frac{1}{3} \beta _0^{(\chi ')}\right) . \end{aligned}$$

(9.16)

Using (8.40) and (3.90) we find

$$\begin{aligned} E_{h-2}^{J_0}=-\frac{\gamma }{\gamma -1}\frac{2}{\lambda \hat{v}({\mathbf {0}})\sqrt{2\rho _0}}\,\frac{1}{A_h C_h }\, \mu _h^2\, \frac{E_h}{Z_h} \beta ^{(2)}_0, \end{aligned}$$

(9.17)

so that, recalling that at lowest order $E_h=1$ and $Z_h=2\lambda \rho _0\hat{v}({\mathbf {0}})$,

$$\begin{aligned} -2E_{h-2}^{J_0}-2\sqrt{2\rho _0}B_{h-2}=-\frac{4}{3}\sqrt{2\rho _0}\frac{\mu ^2_h}{A_h Z_h} \frac{\gamma }{\gamma -1}\beta _0^{(\chi ')}. \end{aligned}$$

(9.18)

We now want to verify that the sum of the two correction terms in the r.h.s. of (9.15) gives exactly the same contribution.

The leading order contribution to the correction term $\partial ^2_{p_0}\hat{W}_{0,1;J^\Delta }^{(h-1)}({\mathbf {0}})$ is represented on the second line of Fig. 25. Using the same notations as in Appendix 3.6, we find

$$\begin{aligned} \partial ^2_{p_0}\hat{W}_{0,1;J^\Delta }^{(h-1)}({\mathbf {0}})&= - 4\lambda \rho _0\hat{v} (\vec {0}) \,\gamma ^{-h/2}\mu _h\,\frac{1}{A_hZ_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} \left( \frac{1}{\sum _{k\ge 0}{\mathfrak {f}}_k(|\mathbf{k}|)} -1 \right) {\mathfrak {f}}_0(|\mathbf{k}|)\nonumber \\&\qquad \cdot \partial ^2_{p_0} \left[ \, \left( 1+\alpha _hp_0 \frac{k_0}{|\mathbf{k}|^2}\right) \frac{{\mathfrak {f}}_0(|\mathbf{k}+\mathbf{p}|)}{|\mathbf{k}+\mathbf{p}|^2} \right] _{\mathbf{p}=\mathbf{0}}, \end{aligned}$$

(9.19)

that is, using also the fact that at lowest order $\alpha _h=1$ and $Z_h=2\lambda \rho _0\hat{v} (\vec {0})$,

$$\begin{aligned} \partial ^2_{p_0}\hat{W}_{0,1;J^\Delta }^{(h-1)}({\mathbf {0}})&= - 2 \,\frac{\gamma ^{-h/2}\mu _h}{A_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} u_0(|\mathbf{k}|) \left[ \frac{2k_0}{|\mathbf{k}|^2}\partial _{k_0}\left( \frac{{\mathfrak {f}}_0(|\mathbf{k}|)}{|\mathbf{k}|^2}\right) +\partial ^2_{k_0} \left( \frac{{\mathfrak {f}}_0(|\mathbf{k}|)}{|\mathbf{k}|^2}\right) \right] . \end{aligned}$$

(9.20)

We now compute the derivatives and pass to polar coordinates, thus finding

$$\begin{aligned} \partial ^2_{p_0}\hat{W}_{0,1;J^\Delta }^{(h-1)}({\mathbf {0}})&= - \frac{2\gamma ^{-h/2}\mu _h}{A_h} \int \frac{d^3 \mathbf{k}}{(2\pi )^3} u_0(|\mathbf{k}|) \nonumber \\&\quad \left[ \frac{2 {\mathfrak {f}}_0(|\mathbf{k}|) }{|\mathbf{k}|^6}\left( k_0^2- |\vec k|^2\right) + \frac{{\mathfrak {f}}'_0(|\mathbf{k}|) }{|\mathbf{k}|^5} \left( |\vec k|^2-2k_0^2\right) + {\mathfrak {f}}''_0(|\mathbf{k}|) \frac{k_0^2}{|\mathbf{k}|^4} \right] \nonumber \\&=\frac{\gamma ^{-h/2}\mu _h}{A_h}\frac{1}{2\pi ^2} \int d\rho \, u_0(\rho ) \left[ \frac{4}{3}\frac{{\mathfrak {f}}_0(\rho )}{\rho ^2} - \frac{2}{3} {\mathfrak {f}}''_0(\rho ) \right] . \end{aligned}$$

(9.21)

The leading order contribution to the correction term $\partial ^2_{p_0}\hat{W}_{0,1;J^{\delta T}}^{(h-1)}({\mathbf {0}})$ is represented on the third line of Fig. 25, and is equal to

$$\begin{aligned}&\partial ^2_{p_0}\hat{W}_{0,1;J^{\delta T}}^{(h-1)}({\mathbf {0}}) = -2 \frac{\gamma ^{-\frac{h}{2}}\mu _hE_h}{A_hC_h Z_h}\nonumber \\&\quad \int \frac{d^3\mathbf{k}}{(2\pi )^3} k_0\left( \frac{1}{\sum _{k\ge 0}{\mathfrak {f}}_k(|\mathbf{k}|)} -1 \right) \frac{{\mathfrak {f}}_0(|\mathbf{k}|)}{|\mathbf{k}|^2}\partial _{p_0}^2\left[ p_0\frac{{\mathfrak {f}}_0(|\mathbf{k}+\mathbf{p}|)}{|\mathbf{k}+\mathbf{p}|^2}\right] _{\mathbf{p}={\mathbf {0}}}\nonumber \\&\quad =\frac{\gamma ^{-h/2}\mu _h}{A_h}\frac{E_h}{C_hZ_h}\frac{1}{2\pi ^2} \int d\rho \, u_0(\rho ) \left[ \frac{8}{3}\frac{{\mathfrak {f}}_0(\rho )}{\rho ^2} - \frac{4}{3} \frac{{\mathfrak {f}}'_0(\rho )}{\rho } \right] . \end{aligned}$$

(9.22)

Using the fact that at lowest order $E_h/(C_hZ_h)=1$, we find that the difference between (9.21) and (9.22) is

$$\begin{aligned} \partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^\Delta }({\mathbf {0}})-\partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^{\delta T}}({\mathbf {0}})&= \frac{\gamma ^{-h/2}\mu _h}{A_h}\frac{1}{2\pi ^2} \int d\rho \, u_0(\rho )\nonumber \\&\bigg [-\frac{4}{3}\frac{{\mathfrak {f}}_0(\rho )}{\rho ^2}+\frac{4}{3}\frac{{\mathfrak {f}}_0'(\rho )}{\rho } - \frac{2}{3} {\mathfrak {f}}''_0(\rho ) \bigg ]. \end{aligned}$$

(9.23)

Using the first of (9.4), we can rewrite this equation as

$$\begin{aligned} \partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^\Delta }({\mathbf {0}})-\partial ^2_{p_0}\hat{W}^{(h-1)}_{0,1;J^{\delta T}}({\mathbf {0}})&= -\frac{4}{3}\sqrt{2\rho _0} \frac{\mu _h^2}{A_h}\frac{1}{2\pi ^2} \int d\rho \, u_0(\rho ) \nonumber \\&\bigg [2\frac{{\mathfrak {f}}_0(\rho )}{\rho ^2}-2\frac{{\mathfrak {f}}_0'(\rho )}{\rho } + {\mathfrak {f}}''_0(\rho ) \bigg ] \end{aligned}$$

(9.24)

that, after an integration by parts, can be easily recognized to be the same as (9.18).

Fig. 25

Diagrams involved in the local WI relating $B_h$ and $E_h$. On the first line the lowest order beta function for $B_h$ and $E^{J_0}_h$. On the second and third lines, the correction terms coming from the cutoffs