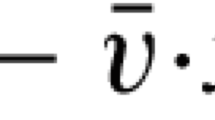Skip to main content
SpringerLink
Log in

Newton-Type Methods: A Broader View

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

We discuss the question of which features and/or properties make a method for solving a given problem belong to the “Newtonian class.” Is it the strategy of linearization (or perhaps, second-order approximation) of the problem data (maybe only part of the problem data)? Or is it fast local convergence of the method under natural assumptions and at a reasonable computational cost of its iteration? We consider both points of view, and also how they relate to each other. In particular, we discuss abstract Newtonian frameworks for generalized equations, and how a number of important algorithms for constrained optimization can be related to them by introducing structured perturbations to the basic Newton iteration. This gives useful tools for local convergence and rate-of-convergence analysis of various algorithms from unified perspectives, often yielding sharper results than provided by other approaches. Specific constrained optimization algorithms, which can be conveniently analyzed within perturbed Newtonian frameworks, include the sequential quadratic programming method and its various modifications (truncated, augmented Lagrangian, composite step, stabilized, and equipped with second-order corrections), the linearly constrained Lagrangian methods, inexact restoration, sequential quadratically constrained quadratic programming, and certain interior feasible directions methods. We recall most of those algorithms as examples to illustrate the underlying viewpoint. We also discuss how the main ideas of this approach go beyond clearly Newton-related methods and are applicable, for example, to the augmented Lagrangian algorithm (also known as the method of multipliers), which is in principle not of Newton type since its iterations do not approximate any part of the problem data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Izmailov, A.F., Kurennoy, A.S.: Abstract Newtonian frameworks and their applications. SIAM J. Optim. 23, 2369–2396 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  2. Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer-Verlag, New York (2003)

    Google Scholar 

  3. Bonnans, J.F.: Local analysis of Newton-type methods for variational inequalities and nonlinear programming. Appl. Math. Optim. 29, 161–186 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  4. Fischer, A.: Local behavior of an iterative framework for generalized equations with nonisolated solutions. Math. Program. 94, 91–124 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  5. Klatte, D., Kummer, B.: Nonsmooth Equations in Optimization: Regularity, Calculus, Methods and Applications. Kluwer Academic Publishers, Dordrecht (2002)

    Google Scholar 

  6. Robinson, S.M.: Newton’s method for a class of nonsmooth functions. Set-Valued Anal. 2, 291–305 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  7. Robinson, S.M.: A point-of-attraction result for Newton’s method with point-based approximations. Optimization 60, 89–99 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Dontchev, A.L., Rockafellar, R.T.: Implicit Functions and Solution Mappings. Springer, New York (2009)

    Book  MATH  Google Scholar 

  9. Izmailov, A.F., Solodov, M.V.: Inexact Josephy–Newton framework for generalized equations and its applications to local analysis of Newtonian methods for constrained optimization. Comput. Optim. Appl. 46, 347–368 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Izmailov, A.F., Solodov, M.V.: A truncated SQP method based on inexact interior-point solutions of subproblems. SIAM J. Optim. 20, 2584–2613 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  11. Wright, S.J.: Superlinear convergence of a stabilized SQP method to a degenerate solution. Comput. Optim. Appl. 11, 253–275 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  12. Hager, W.W.: Stabilized sequential quadratic programming. Comput. Optimizat. Appl. 12, 253–273 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  13. Fernández, D., Solodov, M.: Stabilized sequential quadratic programming for optimization and a stabilized Newton-type method for variational problems. Math. Program. 125, 47–73 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  14. Izmailov, A.F., Solodov, M.V.: Stabilized SQP revisited. Math. Program. 133, 93–120 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  15. Solodov, M.V.: Constraint qualifications. In: Cochran, J.J. (ed.) Wiley Encyclopedia of Operations Research and Management Science. Wiley, New York (2010)

    Google Scholar 

  16. Robinson, S.M.: A quadratically convergent algorithm for general nonlinear programming problems. Math. Program. 3, 145–156 (1972)

    Article  MATH  Google Scholar 

  17. Murtagh, B.A., Saunders, M.A.: A projected Lagrangian algorithm and its implementation for sparse nonlinear constraints. Math. Program. Study 16, 84–117 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  18. Friedlander, M.P., Saunders, M.A.: A globally convergent linearly constrained Lagrangian method for nonlinear optimization. SIAM J. Optim. 15, 863–897 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  19. Martínez, J.M.: Inexact restoration method with Lagrangian tangent decrease and new merit function for nonlinear programming. J. Optim. Theory Appl. 111, 39–58 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  20. Birgin, E.G., Martínez, J.M.: Local convergence of an inexact-restoration method and numerical experiments. J. Optim. Theory Appl. 127, 229–247 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Fischer, A., Friedlander, A.: A new line search inexact restoration approach for nonlinear programming. Comput. Optim. Appl. 46, 333–346 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  22. Fernández, D., Pilotta, E.A., Torres, G.A.: An inexact restoration strategy for the globalization of the sSQP method. Comput. Optim. Appl. 54, 595–617 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  23. Wiest, E.J., Polak, E.: A generalized quadratic programming-based phase-I–II method for inequality-constrained optimization. Appl. Math. Optim. 26, 223–252 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  24. Kruk, S., Wolkowicz, H.: Sequential, quadratically constrained, quadratic programming for general nonlinear programming. In: Wolkowicz, H., Saigal, R., Vandenberghe, L. (eds.) Handbook of Semidefinite Programming, pp. 563–575. Kluwer Academic Publishers, Dordrecht (2000)

    Chapter  Google Scholar 

  25. Anitescu, M.: A superlinearly convergent sequential quadratically constrained quadratic programming algorithm for degenerate nonlinear programming. SIAM J. Optim. 12, 949–978 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  26. Fukushima, M., Luo, Z.-Q., Tseng, P.: A sequential quadratically constrained quadratic programming method for differentiable convex minimization. SIAM J. Optim. 13, 1098–1119 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  27. Solodov, M.V.: On the sequential quadratically constrained quadratic programming methods. Math. Oper. Res. 29, 64–79 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  28. Fernández, D., Solodov, M.V.: On local convergence of sequential quadratically-constrained quadratic-programming type methods, with an extension to variational problems. Comput. Optim. Appl. 39, 143–160 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  29. Vardi, A.: A trust region algorithm for equality constrained minimization: convergence properties and implementation. SIAM J. Numer. Anal. 22, 575–591 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  30. Omojokun, E.O.: Trust region algorithms for optimization with nonlinear equality and inequality constraints. Ph.D. thesis. Department of Computer Science, University of Colorado at Boulder, (1989)

  31. Fletcher, R.: Second order corrections for non-differentiable optimization. In: Griffiths, D. (ed.) Numerical Analysis, pp. 85–114. Springer-Verlag, Berlin (1982)

    Chapter  Google Scholar 

  32. Herskovits, J.: A two-stage feasible direction algorithm including variable metric techniques for nonlinear optimization problems. Rapport de Recherche 118. INRIA, Rocqencourt, (1982)

  33. Herskovits, J.: A two-stage feasible directions algorithm for nonlinear constrained optimization. Math. Program. 36, 19–38 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  34. Herskovits, J.: Feasible direction interior-point technique for nonlinear optimization. J. Optim. Theory Appl. 99, 121–146 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  35. Panier, E.R., Tits, A.L., Herskovits, J.: A QP-free, globally convergent, locally superlinearly convergent algorithm for inequality constrained optimization. SIAM J. Control Optim. 26, 788–811 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  36. Tits, A.L., Wächter, A., Bakhtiari, S., Urban, T.J., Lawrence, C.T.: A primal-dual interior-point method for nonlinear programming with strong global and local convergence properties. SIAM J. Optim. 14, 173–199 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  37. Izmailov, A.F., Kurennoy, A.S., Solodov, M.V.: Some composite-step constrained optimization methods interpreted via the perturbed sequential quadratic programming framework. Optim. Method. Softw. (to appear)

  38. Izmailov, A.F., Solodov, M.V.: Newton-Type Methods for Optimization and Variational Problems. Springer Series in Operations Research and Financial Engineering. Springer International Publishing, Switzerland (2014)

    Book  MATH  Google Scholar 

  39. Hestenes, M.R.: Multiplier and gradient methods. J. Optim. Theory Appl. 4, 303–320 (1969)

    Article  MATH  MathSciNet  Google Scholar 

  40. Powell, M.J.D.: A method for nonlinear constraints in minimization problems. In: Fletcher, R. (ed.) Optimization, pp. 283–298. Academic Press, New York (1969)

    Google Scholar 

  41. Conn, A.R., Gould, N., Sartenaer, A., Toint, P.L.: Convergence properties of an augmented Lagrangian algorithm for optimization with a combination of general equality and linear constraints. SIAM J. Optim. 6, 674–703 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  42. Andreani, R., Birgin, E.G., Martínez, J.M., Schuverdt, M.L.: On augmented Lagrangian methods with general lower-level constraints. SIAM J. Optim. 18, 1286–1309 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  43. Fernández, D., Solodov, M.V.: Local convergence of exact and inexact augmented Lagrangian methods under the second-order sufficient optimality condition. SIAM J. Optim. 22, 384–407 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  44. Josephy, N.H.: Newton’s method for generalized equations. Technical Summary Report 1965. Mathematics Research Center, University of Wisconsin, Madison, WI (1979)

  45. Rockafellar, R.T., Wets, J.B.: Variational Analysis. Springer-Verlag, Berlin (1998)

    Book  MATH  Google Scholar 

  46. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

    MATH  Google Scholar 

  47. Bonnans, J.F., Shapiro, A.: Perturbation Analysis of Optimization Problems. Springer-Verlag, New York (2000)

    Book  MATH  Google Scholar 

  48. Giannessi, F.: Constrained Optimization and Image Space Analysis. Springer-Verlag, New York (2005)

    MATH  Google Scholar 

  49. Boggs, P., Tolle, J.: Sequential quadratic programming. Acta Numer. 4, 1–51 (1995)

    Article  MathSciNet  Google Scholar 

  50. Gill, P.E., Wong, E.: Sequential quadratic programming methods. In: Lee, J., Leyffer, S. (eds.) Mixed Integer Nonlinear Programming. The IMA Volumes in Mathematics and its Applications, vol. 154, pp. 147–224. Springer-Verlag, Berlin (2012)

    Chapter  Google Scholar 

  51. Rademacher, H.: Über partielle und totale differenzierbarkeit I. Math. Ann. 89, 340–359 (1919)

    Article  MathSciNet  Google Scholar 

  52. Dontchev, A.L., Rockafellar, R.T.: Newton’s method for generalized equations: a sequential implicit function theorem. Math. Program. 123, 139–159 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  53. Robinson, S.M.: Strongly regular generalized equations. Math. Oper. Res. 5, 43–62 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  54. Izmailov, A.F.: Strongly regular nonsmooth generalized equations. Math. Program. (2013). doi:10.1007/s10107-013-0717-1

    MathSciNet  Google Scholar 

  55. Kojima, M.: Strongly stable stationary solutions in nonlinear programs. In: Robinson, S.M. (ed.) Analysis and Computation of Fixed Points, pp. 93–138. Academic Press, New York (1980)

    Chapter  Google Scholar 

  56. Bonnans, J.F., Sulem, A.: Pseudopower expansion of solutions of generalized equations and constrained optimization. Math. Program. 70, 123–148 (1995)

    MATH  MathSciNet  Google Scholar 

  57. Dontchev, A.L., Rockafellar, R.T.: Characterizations of strong regularity for variational inequalities over polyhedral convex sets. SIAM J. Optim. 6, 1087–1105 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  58. Izmailov, A.F., Kurennoy, A.S., Solodov, M.V.: A note on upper Lipschitz stability, error bounds, and critical multipliers for Lipschitz-continuous KKT systems. Math. Program. 142, 591–604 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  59. Izmailov, A.F., Kurennoy, A.S., Solodov, M.V.: The Josephy–Newton method for semismooth generalized equations and semismooth SQP for optimization. Set-Valued Var. Anal. 21, 17–45 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  60. Josephy, N.H.: Quasi-Newton methods for generalized equations. Technical Summary Report 1966. Mathematics Research Center, University of Wisconsin, Madison, WI (1979)

  61. Mifflin, R.: Semismooth and semiconvex functions in constrained optimization. SIAM J. Control Optim. 15, 959–972 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  62. Conn, A.R., Gould, N.I.M., Toint, PhL: Trust-Region Methods. SIAM, Philadelphia (2000)

    Book  MATH  Google Scholar 

  63. Bonnans, J.F., Gilbert, JCh., Lemaréchal, C., Sagastizábal, C.: Numerical Optimization: Theoretical and Practical Aspects, 2nd edn. Springer-Verlag, Berlin (2006)

    Google Scholar 

  64. Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (2006)

    MATH  Google Scholar 

  65. Wilson, R.B.: A simplicial algorithm for concave programming. Ph.D. thesis. Graduate School of Business Administration, Harvard University (1963)

  66. Robinson, S.M.: Perturbed Kuhn–Tucker points and rates of convergence for a class of nonlinear-programming algorithms. Math. Program. 7, 1–16 (1974)

    Article  MATH  Google Scholar 

  67. Bertsekas, D.P.: Constrained Optimization and Lagrange Multiplier Methods. Academic Press, New York (1982)

    MATH  Google Scholar 

  68. Fernández, D., Izmailov, A.F., Solodov, M.V.: Sharp primal superlinear convergence results for some Newtonian methods for constrained optimization. SIAM J. Optim. 20, 3312–3334 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  69. Dembo, R.S., Eisenstat, S.C., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400–408 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  70. Gould, N.I.M.: Some reflections on the current state of active-set and interior-point methods for constrained optimization. Numerical Analysis Group Internal Report 2003–1. Computational Science and Engineering Department, Rutherford Appleton Laboratory, Oxfordshire (2003)

  71. Gould, N.I.M., Orban, D., Toint, PhL: Numerical methods for large-scale nonlinear optimization. Acta Numer. 14, 299–361 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  72. Leibfritz, F., Sachs, E.W.: Inexact SQP interior point methods and large scale optimal control problems. SIAM J. Control Optim. 38, 272–293 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  73. Murtagh, B.A., Saunders, M.A.: MINOS 5.0 user’s guide. Technical Report SOL 83.20. Stanford University (1983)

  74. Martínez, J.M., Pilotta, E.A.: Inexact restoration algorithms for constrained optimization. J. Optim. Theory Appl. 104, 135–163 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  75. Martínez, J.M., Pilotta, E.A.: Inexact restoration methods for nonlinear programming: advances and perspectives. In: Qi, L.Q., Teo, K.L., Yang, X.Q. (eds.) Optimization and Control with Applications, pp. 271–292. Springer, Berlin (2005)

    Chapter  Google Scholar 

  76. Maratos, N.: Exact penalty function algorithms for finite dimensional and control optimization problems. Ph.D. thesis. University of London (1978)

  77. Li, D.-H., Qi, L.: Stabilized SQP method via linear equations. Applied Mathematics Technical Reptort AMR00/5. University of New South Wales, Sydney (2000)

  78. Wright, S.J.: Modifying SQP for degenerate problems SIAM. J. Optim. 13, 470–497 (2002)

    MATH  Google Scholar 

  79. Wright, S.J.: Constraint identification and algorithm stabilization for degenerate nonlinear programs. Math. Program. 95, 137–160 (2003)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

Research of the first author is supported by the Russian Foundation for Basic Research Grant 14-01-00113. The second author is supported in part by CNPq Grant 302637/2011-7, by PRONEX–Optimization, and by FAPERJ.

Author information

Authors and Affiliations

  1. Moscow State University, MSU, OR Department, VMK Faculty, Uchebniy Korpus 2, Leninskiye Gory, 119991,  Moscow, Russia

    A. F. Izmailov

  2. IMPA – Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, Jardim Botânico, Rio de Janeiro, RJ, 22460-320,  Brazil

    M. V. Solodov

Authors
  1. A. F. Izmailov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. V. Solodov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. V. Solodov.

Additional information

Communicated by Aram Arutyunov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Izmailov, A.F., Solodov, M.V. Newton-Type Methods: A Broader View. J Optim Theory Appl 164, 577–620 (2015). https://doi.org/10.1007/s10957-014-0580-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-014-0580-0

Keywords

Mathematics Subject Classification

Search

Navigation