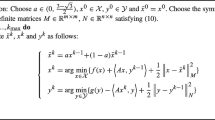Abstract
In this paper, we focus on subspace learning problems on the Grassmann manifold. Interesting applications in this setting include low-rank matrix completion and low-dimensional multivariate regression, among others. Motivated by privacy concerns, we aim to solve such problems in a decentralized setting where multiple agents have access to (and solve) only a part of the whole optimization problem. The agents communicate with each other to arrive at a consensus, i.e., agree on a common quantity, via the gossip protocol. We propose a novel cost function for subspace learning on the Grassmann manifold, which is a weighted sum of several sub-problems (each solved by an agent) and the communication cost among the agents. The cost function has a finite-sum structure. In the proposed modeling approach, different agents learn individual local subspaces but they achieve asymptotic consensus on the global learned subspace. The approach is scalable and parallelizable. Numerical experiments show the efficacy of the proposed decentralized algorithms on various matrix completion and multivariate regression benchmarks.
Similar content being viewed by others
1 Introduction
Learning a low-dimensional representation of vast amounts of data is a fundamental problem in machine learning. It is motivated by considerations of low memory footprint or low computational complexity, model compression, better generalization performance, robustness to noise, among others. The applicability of low-dimensional modeling is ubiquitous, including images in computer vision, text documents in natural language processing, genomics data in bioinformatics, and customers’ record or purchase history in recommender systems.
Principal component analysis (PCA) is one of the most well known algorithms employed for low-dimensional representation in data analysis (Bishop 2006). PCA is employed to learn a low-dimensional subspace that captures the most variability in the given data. Collaborative filtering based applications, such as movie or product recommendation, desire learning a latent low-dimensional subspace that captures users’ preferences (Rennie and Srebro 2005; Zhou et al. 2008; Abernethy et al. 2009). The underlying assumption here is that similar users have similar preferences. A common approach to model this problem is via low-rank matrix completion: recovering low-rank matrices when most entries are unknown (Candès and Recht 2009; Cai et al. 2010; Wen et al. 2012). Motivated by similar requirements of learning a low-dimensional subspace, low-rank matrix completion algorithms are also employed in other applications such as system identification (Markovsky and Usevich 2013), subspace identification (Balzano et al. 2010), sensor networks (Keshavan et al. 2009), and gene expression prediction (Kapur et al. 2016), to name a few.
In several multivariate regression problems, we need to learn the model parameters for several related regression tasks (problems), but the amount of labeled data available for each task is low. In such data scarce regime, learning each regression problem (task) only with its own labeled data may not give good enough generalization performance (Baxter 1997, 2000; Jalali et al. 2010; Álvarez et al. 2012; Zhang and Yang 2017). The paradigm of multitask learning (Caruana 1997) advocates learning these related tasks jointly, i.e., each tasks not only learns from its own labeled data but also from the labeled data of other tasks. Multitask learning is helpful when the tasks are related, e.g., the model parameters of all the tasks have some common characteristics that may be exploited during the learning phase. Existing multitask literature have explored various ways of learning the tasks jointly (Evgeniou and Pontil 2004; Jacob et al. 2008; Zhang and Yeung 2010; Zhong and Kwok 2012; Jawanpuria and Nath 2012; Kumar and Daume 2012; Zhang 2015). Enforcing the model parameters of all the tasks to share a common low-dimensional latent feature space is a common approach in multitask (feature) learning (Ando and Zhang 2005; Amit et al. 2007; Argyriou et al. 2008).
A low-dimensional subspace can be viewed as an instance of the Grassmann manifold \({\mathrm {Gr}({r},{m})}\), which is the set of r-dimensional subspaces in \(\mathbb {R}^m\). A number of Grassmann algorithms exploiting the geometry of the search space exist for subspace learning, in both batch (Absil et al. 2008) and online variants (Bonnabel 2013; Zhang et al. 2016; Sato et al. 2017). Several works (Balzano et al. 2010; Dai et al. 2011; He et al. 2012; Boumal and Absil 2015) discuss a subspace learning approach based on the Grassmann geometry from incomplete data. Meyer et al. (2009, 2011) exploit the Grassmann geometry in distance learning problems through low-rank subspace learning. More recently, Harandi et al. (2016, 2017, 2018) show the benefit of the Grassmann geometry in low-dimensional dictionary and metric learning problems. Subspace constraints are also employed in many applications of computer vision and medical image analysis (Cetingul and Vidal 2009; Turaga et al. 2008).
In this paper, we are interested in a decentralized learning setting on the Grassmann manifold, which is less explored for the considered class of problems. To this end, we assume that the given data is distributed across several agents, e.g., different computer systems. The agents can learn a low-dimensional subspace only from the data that resides locally within them, and cannot access data residing within other agents. This scenario is common in situations where there are privacy concerns of sharing sensitive data. Ling et al. (2012), Lin and Ling (2015) discuss decentralized algorithms for the problem of low-rank matrix completion. The agents can communicate with each other to develop consensus over a required objective, which in our case, is the low-dimensional subspace. The communication between agents causes additional computational overheads, and hence should ideally be as little as possible. This, in addition to privacy concerns, motivate us to employ the so-called gossip protocol in our setting (Boyd et al. 2006; Shah 2009; Colin et al. 2016). In the gossip framework, an agent communicates with only one other agent at a time (Boyd et al. 2006). The gossip framework has been also explored in several works in the context of optimization for machine learning problems (Jin et al. 2016; Ormándi et al. 2013; Blot et al. 2016).
Recently, Bonnabel (2013, Section 4.4) discusses a non-linear gossip algorithm for estimating covariance matrix \(\mathbf{W}\) on a sensor network of multiple agents. Each agent is initialized with a local covariance matrix estimate, and the aim there is to reach a common (average) covariance matrix estimate via communication among the agents. If \(\mathbf{W}_i\) is the estimate of the covariance matrix possessed by agent i, Bonnabel (2013) proposes to minimize the cost function
to arrive at consensus, where the total number of agents is m and d is a distance function between covariance matrix estimates. At each time slot, a randomly chosen agent \(i(<m)\) communicates with its neighbor agent \(i+1\) and both update their covariance matrix estimates. Bonnabel (2013) shows that under mild assumptions, the agents converge to a common covariance matrix estimate, i.e., the agents achieve consensus. It should be noted that consensus learning on manifolds has been in general a topic of much research, e.g., Sarlette and Sepulchre (2009) and Tron et al. (2011, 2013) study the dynamics of agents which share their relative states over a more complex communication graph (than the one in (Bonnabel 2013, Section 4.4)) . The aim in (Sarlette and Sepulchre 2009; Tron et al. 2011, 2013; Bonnabel 2013) is to make the agents converge to a single point. In this paper, however, we dwell on consensus learning of agents along with optimizing the sub-problems handled by the agents. For example, at every time instance a randomly chosen agent locally updates its local subspace (e.g., with a gradient update) and simultaneously communicates with its neighbor to build a consensus on the global subspace. This is a typical set up encountered in machine learning based applications. The paper does not aim at a comprehensive treatment of consensus algorithms on manifolds, but rather focuses on the role of the Grassmann geometry in coming out with a simple cost problem formulation for decentralized subspace learning problems.
We propose a novel optimization formulation on the Grassmann manifold that combines together a weighted sum of tasks (accomplished by agents individually) and consensus terms (that couples subspace information transfer among agents). The weighted formulation allows an implicit averaging of agents at every time slot. The formulation allows to readily propose a stochastic gradient algorithm on the Grassmann manifold and further allows a parallel implementation (via a modified sampling strategy). For dealing with ill-conditioned data, we also propose a preconditioned variant, which is computationally efficient to implement. We apply the proposed approach on two popular subspace learning problems: low-rank matrix completion (Cai et al. 2010; Keshavan et al. 2010; Balzano et al. 2010; Boumal and Absil 2015, 2011; Dai et al. 2011) and multitask feature learning (Ando and Zhang 2005; Argyriou et al. 2008; Zhang et al. 2008; Zhang and Yang 2017). Empirically, the proposed algorithms compete effectively with state-of-the-art on various benchmarks.
The organization of the paper is as follows. Section 2 presents a discussion on the Grassmann manifold. Both low-rank matrix completion and multitask feature learning problems are motivated in Sect. 3 as finite-sum problems on the Grassmann manifold. In Sect. 4, we discuss the decentralized learning setup and propose a novel problem formulation. In Sect. 5, we discuss the proposed stochastic gradient based gossip algorithm along with preconditioned and parallel variants. Experimental results are discussed in Sect. 6. The present paper extends the unpublished technical report (Mishra et al. 2016). The Matlab codes for the proposed algorithms are available at https://bamdevmishra.in/gossip.
2 Grassmann manifold
The Grassmann manifold \({\mathrm {Gr}({r},{m})}\) is the set of r-dimensional subspaces in \(\mathbb {R}^m\). In matrix representation, an element of \({\mathrm {Gr}({r},{m})}\) is represented by the column space of a full rank matrix of size \(m\times r\). Equivalently, if \(\mathbf{U}\) is a full rank matrix of size \(m \times r\), an element of \({\mathrm {Gr}({r},{m})}\) is represented as
Without loss of generality, we impose orthogonality on \(\mathbf{U}\), i.e., \(\mathbf{U}^\top {\mathbf{U}} = \mathbf{I}\). This characterizes the columns space in (1) and allows to represent \(\mathcal {U}\) as follows:
where \({\mathcal {O}({r})}\) denotes the orthogonal group, i.e., the set of \(r\times r\) orthogonal matrices. An implication of (2) is that each element of \({\mathrm {Gr}({r},{m})}\) is an equivalence set. This allows the Grassmann manifold to be treated as a quotient space of the larger Stiefel manifold \({\mathrm {St}({r},{m})}\), which is the set of matrices of size \(m\times r\) with orthonormal columns. Specifically, the Grassmann manifold has the quotient manifold structure
A popular approach to optimization on a quotient manifold is to recast it to into a Riemannian optimization framework (Edelman et al. 1998; Absil et al. 2008). In this setup, while optimization is conceptually on the Grassmann manifold \({\mathrm {Gr}({r},{m})} \), numerically, it allows to implement operations with concrete matrices, i.e., with elements of \({\mathrm {St}({r},{m})}\). Geometric objects on the quotient manifold can be defined by means of matrix representatives. Below, we show the development of various geometric objects that are are required to optimize a smooth cost function on the quotient manifold with a first-order algorithm (including the stochastic gradient algorithm). Most of these notions follow directly from (Absil et al. 2008).
A fundamental requirement is the characterization of the linearization of the Grassmann manifold, which is the called its tangent space. Since the Grassmann manifold is the quotient space of the Stiefel manifold, shown in (3), its tangent space has matrix representation in terms of the tangent space of the larger Stiefel manifold \( {\mathrm {St}({r},{m})}\). Endowing the Grassmann manifold with a Riemannian submersion structure (Absil et al. 2008), the tangent space of \( {\mathrm {St}({r},{m})}\) at \(\mathbf{U}\) has the characterization
The tangent space of \({\mathrm {Gr}({r},{m})}\) at an element \(\mathcal {U}\) identifies with a subspace of \(T_{\mathbf{U}} {\mathrm {St}({r},{m})}\) (4), and specifically, which has the matrix characterization, i.e.,
where \(\mathbf{U}\) is the matrix characterization of \(\mathcal {U}\). In (5), the vector \(\xi _{\mathbf{U}}\) is the matrix characterization of the abstract tangent vector \(\xi _{\mathcal {U}} \in T_{\mathcal {U}} {\mathrm {Gr}({r},{m})}\) at \(\mathcal {U} \in {\mathrm {Gr}({r},{m})}\).
A second requirement is the computation of the Riemannian gradient of a cost function, say \(f : {\mathrm {Gr}({r},{m})} \rightarrow \mathbb {R}\). Again exploiting the quotient structure of the Grassmann manifold, the Riemannian gradient \({\mathrm {grad}}_{\mathcal {U}} f\) of f at \(\mathcal {U} \in {\mathrm {Gr}({r},{m})}\) admits the matrix expression
where \({\mathrm {Grad}}_{\mathbf{U}} f\) is the (Euclidean) gradient of f in the matrix space \(\mathbb {R}^{m \times r}\) at \(\mathbf{U}\).
A third requirement is the notion of a straight line along a tangential direction on the Grassmann manifold. This quantity is captured with the exponential mapping operation on the Grassmann manifold. Given a tangential direction \(\xi _{\mathcal {U}} \in T_{\mathcal {U}} {\mathrm {Gr}({r},{m})}\) that has the matrix expression \(\xi _{\mathbf{U}}\) belonging to the subspace (5), the exponential mapping along \(\xi _{\mathbf{U}}\) has the expression (Absil et al. 2008, Section 5.4)
where \(\mathbf{W}\varvec{\Sigma }{} \mathbf{V}^\top \) is the rank-r singular value decomposition of \(\xi _{\mathbf{U}}\). The \(\cos (\cdot )\) and \(\sin (\cdot )\) operations are on the diagonal entries.
Finally, a fourth requirement is the notion of the logarithm map of an element \(\widetilde{\mathcal {U}}\) at \(\mathcal {U}\) on the Grassmann manifold. The logarithm map operation maps \(\widetilde{\mathcal {U}}\) onto a tangent vector at \(\mathcal {U}\), i.e., if \(\widetilde{\mathcal {U}}\) and \(\mathcal {U}\) have matrix operations \(\widetilde{\mathbf{U}}\) and \(\mathbf{U}\), respectively, then the logarithm map finds a vector in (5) at \(\mathbf{U}\). The closed-form expression of the logarithm map \( \mathrm{Log}_{\mathcal {U}} (\widetilde{\mathcal {U}})\), i.e.,
where \(\mathbf{PS} \mathbf{Q}^\top \) is the rank-r singular value decomposition of \((\widetilde{\mathbf{U}} - \mathbf{U} \mathbf{U}^\top \widetilde{\mathbf{U}})(\mathbf{U}^\top \widetilde{\mathbf{U}})^{-1}\) and \(\arctan (\cdot )\) operation is on the diagonal entries.
3 Motivation
We look at a decentralized learning of the subspace learning problem of the form
where \({\mathrm {Gr}({r},{m})}\) is the Grassmann manifold. We assume that the functions \(f_i: \mathbb {R}^{m\times r} \rightarrow \mathbb {R}\) for all \(i=\{1,\ldots ,N \}\) are smooth. In this section, we formulate two popular class of problems as subspace learning problems of the form (8) on the Grassmann manifold. The decentralization learning setting for (8) is considered in Sect. 4.
3.1 Low-rank matrix completion as subspace learning
The problem of low-rank matrix completion amounts to completing a matrix from a small number of entries by assuming a low-rank model for the matrix. The rank constrained matrix completion problem can be formulated as
where \(\Vert \cdot \Vert _F\) is the Frobenius norm, \(\lambda \) is the regularization parameter (Boumal and Absil 2015, 2011), and \({\mathbf{Y }^ \star }\in \mathbb {R}^{n\times m}\) is a matrix whose entries are known for indices if they belong to the subset \((i,j)\in \varOmega \) and \(\varOmega \) is a subset of the complete set of indices \(\{(i,j):i\in \{1,...,m\}\text { and }j\in \{1,...,n\}\}\). The operator \([\mathcal {P}_{\varOmega }(\mathbf{Y})]_{ij}=\mathbf{Y}_{ij}\) if \((i,j) \in \varOmega \) and \([\mathcal {P}_{\varOmega }(\mathbf{Y})]_{ij}=0\) otherwise is called the orthogonal sampling operator and is a mathematically convenient way to represent the subset of known entries. The rank constraint parameter r is usually set to a low value, e.g., \(r \ll (m, n)\). The particular regularization term \(\Vert \mathbf{Y} - \mathcal {P}_{\varOmega }(\mathbf{Y})\Vert _F^2\) in (9) is motivated in (Dai et al. 2011; Boumal and Absil 2015, 2011), and it specifically penalizes the large predictions. An alternative to the regularization term in (9) is \(\Vert \mathbf{Y} \Vert _F^2\).
A way to handle the rank constraint in (9) is by using the parameterization \(\mathbf{Y} = \mathbf{U} \mathbf{W}^\top \), where \(\mathbf{U} \in {\mathrm {St}({r},{m})}\) and \(\mathbf{W} \in \mathbb {R}^{n \times r}\) (Boumal and Absil 2015, 2011; Mishra et al. 2014). The problem (9) reads
The inner least-squares problem in (10) admits a closed-form solution. Consequently, it is straightforward to verify that the outer problem in \(\mathbf{U}\) only depends on the column space of \(\mathbf{U}\), and therefore, is on the Grassmann manifold \({\mathrm {Gr}({r},{m})}\) and not on \({\mathrm {St}({r},{m})}\) (Dai et al. 2012; Boumal and Absil 2015, 2011). Solving the inner problem in closed form, the problem at hand is
where \(\mathbf{W}_{\mathbf{U}}\) is the unique solution to the inner optimization problem in (10) and \(\mathcal {U}\) is the column space of \(\mathbf{U}\) (Dai et al. 2012). It should be noted that (11) is a problem on the Grassmann manifold \({\mathrm {Gr}({r},{m})}\), but computationally handled with matrices \(\mathbf{U}\) in \({\mathrm {St}({r},{m})}\).
Consider the case when \(\mathbf{Y}^\star = [\mathbf{Y}_1^\star , \mathbf{Y}_2^\star ,\ldots , \mathbf{Y}_N^\star ]\) is partitioned along the columns such that the size of \(\mathbf{Y}_i^\star \) is \(m\times n_i\) with \(\sum n_i = n\) for \(i=\{1,2,\ldots , N\}\). \(\varOmega _i\) is the local set of indices for each of the partitions. The column-partitioning of \(\mathbf{Y}^\star \) implies that \(\mathbf{W}^\top \) can also partitioned in (10) along the columns similarly, i.e., \(\mathbf{W}^\top =[\mathbf{W}_1^\top , \mathbf{W}_2^\top ,\ldots , \mathbf{W}_N^\top ]\), where \(\mathbf{W}_i \in \mathbb {R}^{n_i \times r}\). Hence, an equivalent reformulation of (11) is the finite-sum problem
where \(f_i({\mathcal {U}}) :=0.5\Vert \mathcal {P}_{\varOmega _i}({{\mathbf{UW}}}_{i{\mathbf{U}}}^\top ) - \mathcal {P}_{\varOmega _i}(\mathbf{Y}^\star _i)\Vert _F^2 + \lambda \Vert \mathbf{UW}_{i\mathbf{U}}^\top - \mathcal {P}_{\varOmega }(\mathbf{UW}_{i\mathbf{U}}^\top )\Vert _F^2\) and \({{\mathbf{W}}}_{i{\mathbf{U}}}\) is the least-squares solution to \(\mathrm{arg\,min}_{\mathbf{W}_i \in \mathbb {R}^{n_i \times r }} \Vert \mathcal {P}_{\varOmega _i}(\mathbf{UW}_{i }^\top ) - \mathcal {P}_{\varOmega _i}(\mathbf{Y}_i^\star )\Vert _F^2 + \lambda \Vert \mathbf{UW}_{i }^\top - \mathcal {P}_{{\varOmega }_i}(\mathbf{UW}_{i }^\top )\Vert _F^2 \) for each of the data partitions. The problem (12) is of type (8).
3.2 Low-dimensional multitask feature learning as subspace learning
We next transform an important problem in the multitask learning setting (Caruana 1997; Baxter 1997; Evgeniou et al. 2005) as a subspace learning problem on the Grassmann manifold. The paradigm of multitask learning advocates joint learning of related learning problems. A common notion of task-relatedness among different tasks (problems) is as follows: tasks share a latent low-dimensional feature representation (Ando and Zhang 2005; Argyriou et al. 2008; Zhang et al. 2008; Jawanpuria and Nath 2011; Kang et al. 2011). We propose to learn this shared feature subspace. We first introduce a few notations related to multitask setting.
Let T be the number of given tasks, with each task t having \(d_t\) training examples. Let \((\mathbf{X}_t, y_t)\) be the training instances and corresponding labels for task \(t=1,\ldots ,T\), where \(\mathbf{X}_t\in \mathbb {R}^{d_t\times m}\) and \(y_t\in \mathbb {R}^{d_t}\). Argyriou et al. (2008) proposed the following formulation to learn a shared latent feature subspace:
Here, \(\lambda \) is the regularization parameter, \(\mathbf{O}\) is an orthogonal matrix of size \(m \times m\) that is shared among T tasks, \(w_t\) is the weight vector (also know as task parameter) for task t, and \(\mathbf{W}:=[w_1, w_2, \ldots , w_T]^\top \). The term \(\Vert \mathbf{W^\top }\Vert _{2,1} :=\sum \nolimits _j (\sum \nolimits _i \mathbf{W}_{ij}^2)^{1/2}\) is the (2, 1) norm over the matrix \(\mathbf{W^\top }\). It enforces the group sparse structure (Yuan and Lin 2006) across the columns of \(\mathbf{W}\). The sparsity across columns in \(\mathbf{W}\) ensures that we learn a low-dimensional latent feature representation for the tasks. The basis vectors of this low-dimensional latent subspace are the columns of \(\mathbf{O}\) corresponding to non-zeros columns of \(\mathbf{W}\). Hence, solving (13) leads to a full rank \(m\times m\) latent feature space \(\mathbf{O}\) and performs feature selection (via sparse regularization) in this latent space. This is computationally expensive especially in large-scale applications desiring a low (r) dimensional latent feature representation where \(r\ll m\). In addition, the sparsity inducing 1-norm is non-smooth which poses additional optimization challenges.
We instead learn only the basis vectors of the low-dimensional latent subspace, by restricting the dimension of the subspace (Ando and Zhang 2005; Lapin et al. 2014). The proposed r-dimensional multitask feature learning problem is
where \(\mathbf{U}\) is an \(m\times r\) matrix in \({\mathrm {St}({r},{m})}\) representing the low-dimensional latent subspace. Similar to the earlier matrix completion case, the inner least-squares optimization problem in (14) is solved in closed form by exploiting the least-squares structure. It is readily verified that the outer problem (14) is on \({\mathcal {U}}\), i.e., the search space is the Grassmann manifold. To this end, the problem is
where \(w_{t{\mathbf{U}}}\) is the least-squares solution to \(\mathrm{arg\,min}_{w_t \in \mathbb {R}^{r }} \Vert \mathbf{X}_t \mathbf{U}w_t - y_t \Vert _F^2 + \lambda \Vert w_t\Vert _2^2\). More generally, we distribute the T tasks in (15) into N groups such that \(\sum n_i = T\). This leads to the formulation
where \(\mathcal {T}_i\) is the set of the tasks in group i. The problem (16) is also a particular case of (8).
4 Decentralized subspace learning with gossip
We exploit the finite-sum (sum of N sub cost functions) structure of the problem (8) by distributing the tasks among N agents, which perform certain computations, e.g., computation of the functions \(f_i\) given \({\mathcal {U}}\), independently. Although the computational workload gets distributed among the agents, all agents require the knowledge of the common \({\mathcal {U}}\), which is an obstacle in decentralized learning. To circumvent this issue, instead of one shared subspace \({\mathcal {U}}\) for all agents, each agent i stores a local subspace copy \(\mathcal {U}_i\), which it then updates based on information from its neighbors. For minimizing the communication overhead between agents, we additionally put the constraint that at any time slot only two agents communicate, i.e, each agent has exactly only one neighbor. This is the basis of the standard gossip framework (Boyd et al. 2006). A similar architecture is also exploited in Bonnabel (2013) for decentralized covariance matrix estimation. It should be noted that although we focus on this agent network, our cost formulation can be extended to any arbitrary network of agents.
Following (Bonnabel 2013), the agents are numbered according to their proximity, e.g., for \( i \leqslant N -1\), agents i and \(i + 1\) are neighbors. Equivalently, agents 1 and 2 are neighbors and can communicate. Similarly, agents 2 and 3 communicate, and so on. This communication between the agents allows to reach a consensus on the subspaces \(\mathcal {U}_i\). Our proposed approach to handle the finite-sum problem (8) in a decentralized setting is to solve the problem
where \(d_i\) in (17) is specifically chosen as the Riemannian distance between the subspaces \(\mathcal {U}_i\) and \(\mathcal {U}_{i + 1}\) for \(i\leqslant N-1\) and \(\rho \geqslant 0\) is a parameter that trades off individual (per agent) task minimization with consensus.
For a large \(\rho \), the consensus term in (17) dominates, minimizing which allows the agents to arrive at consensus, i.e., their subspaces converge. For \(\rho = 0\), the optimization problem (17) solves N independent tasks and there is no consensus among the agents. For a sufficiently large \(\rho \), the problem (17) achieves the goal of approximate task solving along with approximate consensus. It should be noted that the consensus term in (17) has only \(N-1\) pairwise distances. For example, (Bonnabel 2013) uses this consensus term structure for covariance matrix estimation. It allows to parallelize subspace learning, as discussed later in Sect. 5.3. Additionally, the standard gossip formulation allows to show the benefit of the trade-off weight \(\rho \) in practical problems.
It should be noted that although we focus on a particular agent-agent network, our cost formulation can be extended to any arbitrary network of agents. For other complex (and communication heavy) agent-agent networks, the consensus part of (17) has additional terms. In particular, let the agent network be a graph G(V, E), where V represents the set of nodes (node \(v_i \in V\) corresponds to agent i) and E represents the set of edges. The edge \(e_{ij} \in E\) between the nodes \(v_i\) and \(v_j\) represents that the nodes communicate. Then, the general formulation is as follows:
where \(d_{ij}\) is the Riemannian distance between the subspaces \(\mathcal {U}_i\) and \(\mathcal {U}_j\). In subsequent sections, we focus on (17) to keep the exposition simple. However, our proposed algorithm and the discussion can be extended to (18).
5 The Riemannian gossip algorithm for (17)
In this section, we focus on proposing a stochastic algorithm for (17) by appropriately sampling the terms in the cost function of (17). This leads to simpler updates of the agent specific subspaces. Additionally, it allows to exploit parallelization of updates. To this end, we exploit the stochastic gradient algorithm framework on Riemannian manifolds (Bonnabel 2013; Sato et al. 2017; Zhang et al. 2016).
As a first step, we reformulate the problem (17) as a single sum problem, i.e.,
where \(g_i(\mathcal {U}_i, \mathcal {U}_{i+1}) := \alpha _i f_k(\mathcal {U}_i) + \alpha _{i+1} f_{i+1}(\mathcal {U}_{i+1}) + 0.5\rho d_k^2 (\mathcal {U}_{i}, \mathcal {U}_{i+1})\). Here, \(\alpha _i\) is a scalar that ensures that the cost functions of (19) and (17) remain the same with the reformulation, i.e., \(\sum g_i = f_1 +\cdots + f_N + 0.5\rho ( d_1^2 (\mathcal {U}_1, \mathcal {U}_2) + d_2 ^2(\mathcal {U}_2, \mathcal {U}_3) +\cdots + d_{N-1} ^2 (\mathcal {U}_{N-1}, \mathcal {U}_{N}) )\). Equivalently, \(\alpha _i = 1\) if \(i=\{1, N \}\), else \(\alpha _i = 0.5\).

At each iteration of the stochastic gradient algorithm, we sample a sub cost function \(g_i\) from the cost function in (19) uniformly at random (we stick to this sampling process for simplicity). Based on the chosen sub cost function, the subspaces \(\mathcal {U}_i\) and \(\mathcal {U}_{i+1}\) are updated by following the negative Riemannian gradient (of the sub cost function \(g_i\)) with a stepsize. The stepsize sequence over the iterations satisfies the conditions that it is square integrable and its summation is divergent (this is explicitly mentioned in the proof of Proposition 1 later).
The overall algorithm is listed as Algorithm 1, which converges to a critical point of (19) almost surely (Bonnabel 2013). An outcome of the updates from Algorithm 1 is that agents 1 and N update twice the number of times the rest of agents update.
The matrix characterizations of implementing Algorithm 1 are shown in Table 1. The development of some of the expressions are discussed earlier in Sect. 2. The asymptotic convergence analysis of Algorithm 1 follows directly from the proposition below.
Proposition 1
Algorithm 1 converges to a first-order critical point of (19).
Proof
The problem (19) can be modeled as
where \(\mathcal {V}:=(\mathcal {U}_1, \mathcal {U}_2,\ldots , \mathcal {U}_N)\), \(\mathcal {M}\) is the Cartesian product of N Grassmann manifolds \({\mathrm {Gr}({r},{m})}\), i.e., \(\mathcal {M}:= \mathrm{Gr}^N(r,m)\), and \(h_i: \mathcal {M} \rightarrow \mathbb {R}: \mathcal {V} \mapsto h_i(\mathcal {V}) = g_i(\mathcal {U}_i, \mathcal {U}_{i+1})\). The updates shown in Algorithm 1 precisely correspond to stochastic gradients updates for the problem (20).
It should be noted that \(\mathcal {M}\) is compact and has a Riemannian structure, and consequently, the problem (20) is an empirical risk minimization problem on a compact manifold. The key idea of the proof is that for a compact Riemannian manifold, all continuous functions of the parameter are bounded, e.g., the Riemannian Hessian of \(h(\mathcal {V})\) is upper bounded for all \(\mathcal {V} \in \mathcal {M}\). We assume that 1) the stepsize sequence satisfies the condition that \(\sum \gamma _k = \infty \) and \( \sum (\gamma _k)^2 < \infty \) and 2) at each time slot k, the stochastic gradient estimate \(\mathrm {grad}_{{\mathcal {V}}} h_i\) is an unbiased estimator of the batch Riemannian gradient \(\sum _i \mathrm {grad}_{\mathcal {V}} h_i\). Under those assumptions, Algorithm 1 converges to a first-order critical point of (19). A rigorous convergence analysis of stochastic gradients on compact manifolds to first-order critical points is presented in (Bonnabel 2013, Theorem 1). \(\square \)
5.1 Computational complexity
For an update of \(\mathcal {U}_i\) with the formulas shown in Table 1, the computational complexity depends on the computation of partial derivatives of the cost functions in (9) and (13), e.g., the gradient \({\mathrm {Grad}}_{\mathcal {U}_i} f_i\) computation of agent i. The three main sources of computations are shown below.
-
1.
Task-related computations
-
Matrix completion problem (9): the computational cost of the partial derivatives for agent i is \(O(|\varOmega _i|r^2 + n_i r ^3 + m r^2)\).
-
Multitask feature learning problem (13): the computational cost of the partial derivatives is \(O(m|\mathcal {T}_i| r^2 + |\mathcal {T}_i| r ^3 + m r^2 + (\sum _{t = \mathcal {T}_i} d_t)m)\), where \(\mathcal {T}_i\) is the group of tasks assigned to agent i.
-
-
2.
Consensus-related computations Communication between agents i and \(i+1\) involves computing \(d_i(\mathcal {U}_i,\mathcal {U}_{i+1})\) which costs \(O(mr^2 + r^3)\).
-
3.
Manifold-related computations Computing the exponential and logarithm mappings cost \(O(mr^2 + r^3)\). Computation of the Riemannian gradient costs \(O(mr^2)\).
As discussed above, the computational cost in the matrix completion problem scales linearly with the number of known entries. In the multitask feature learning problem, the computational cost scales linearly with the number of training examples. In both the problems, the task-related computations dominate over the manifold and consensus related computations, which make the proposed algorithm scalable to large-scale problem instances (shown in Sect. 6).
5.2 Preconditioned variant
The performance of first order algorithms (including stochastic gradients) often depends on the condition number of the Hessian of the cost function (at the minimum). For the matrix completion problem (9), the issue of ill-conditioning arises when data \(\mathbf{Y}^\star \) have power law distributed singular values. Additionally, a large value of \(\rho \) in (17) leads to convergence issues for numerical algorithms. The recent works (Ngo and Saad 2012; Mishra and Sepulchre 2014; Boumal and Absil 2015) exploit the concept of manifold preconditioning for the matrix completion problem (9). In particular, the Riemannian gradients are scaled by computationally cheap matrix terms that arise from the second order curvature information of the cost function. This operation on a manifold requires special attention. In particular, the matrix scaling must be a positive definite operator on the tangent space of the manifold (Mishra and Sepulchre 2014; Boumal and Absil 2015).
Given the Riemannian gradient, e.g, \(\mathrm {grad}_{\mathcal {U}_i} g_i\) for agent i, the proposed preconditioner for (17) is
where \(\mathbf{I}\) is the \(r\times r\) identity matrix. The use of preconditioning (21) costs \(O(n_i r^2 + r^3)\), which is computationally cheap to implement. The term \(\mathbf{W}_{i{\mathbf{U}}_i} ^\top \mathbf{W}_{i{\mathbf{U}}_i}\) captures a block diagonal approximation of the Hessian of the simplified (but related) cost function \( \Vert {{\mathbf{U}_i\mathbf{W}}}_{i{\mathbf{U}_i}}^\top - \mathbf{Y}^\star _i \Vert _F^2\), i.e., an approximation for (9) and (13) (Ngo and Saad 2012; Mishra and Sepulchre 2014; Boumal and Absil 2015). The term \(\rho \mathbf{I}\) is an approximation of the second order derivative of the square of the Riemannian distance. Finally, it should be noted that \({\mathbf{W}_{i{\mathbf{U}}_i} ^\top \mathbf{W}_{i{\mathbf{U}}_i}} + {\rho \mathbf{I}} \succ 0\).
5.3 Parallel variant
The particular structure (also known as the red–black ordering structure in domain decomposition methods) of the cost terms in (19), allows for a straightforward parallel update strategy for solving (19). We look at the following separation of the costs, i.e., the problem is
where the subspace updates corresponding to \(g_{\mathrm{odd}}\) (and similarly \(g_{\mathrm{even}}\)) are parallelizable.
We apply Algorithm 1, where we pick the sub cost function \(g_{\mathrm{odd}}\) (or \(g_{\mathrm{even}}\)) with uniform probability. The key idea is that sampling is on \(g_{\mathrm{odd}}\) and \(g_{\mathrm{even}}\) and not on the sub cost functions \(g_i\) directly. This strategy allows to perform \(\lfloor (N-1)/2 \rfloor \) updates in parallel.
6 Numerical comparisons
Our proposed algorithm (Stochastic Gossip) presented as Algorithm 1 and its preconditioned (Precon Stochastic Gossip) and parallel (Parallel Gossip and Precon Parallel Gossip) variants are compared on various different benchmarks on matrix completion and multitask problems. In many cases, our decentralized gossip algorithms match the generalization performance of competing (tuned) batch algorithms.
Stochastic algorithms with N agents are run for a maximum of \(200(N-1)\) iterations. The parallel variants are run for 400N iterations. Overall, because of the agent–agent network structure, agents 1 and N end up performing a maximum of 200 updates and rest all other agents perform 400 updates. The stepsize sequence is defined as \(\gamma _k = a/(1 + bk)\), where k is the time slot. The constants a and b are set using fivefold cross validation on the training data.
Our implementations are based on the Manopt toolbox (Boumal et al. 2014). All simulations are performed in Matlab on a 2.7 GHz Intel Core i5 machine with 8 GB of RAM. The comparisons on the Netflix and MovieLens-10M datasets are performed on a cluster with larger memory.
6.1 Benefit of the Grassmann geometry against the Euclidean geometry
In contrast to the proposed formulation (17), an alternative is to consider the formulation
where the problem is in the Euclidean space and the consensus among the agents is with respect to the Euclidean distance. Although this alternative choice is appealing for its numerical simplicity, the benefit of exploiting the geometry of the problem is shown in Fig. 1. We consider a matrix completion problem instance in Fig. 1, where we apply Stochastic Gossip algorithms with \(N=6\) agents. Figure 1 shows the performance of only two agents for clarity, where agent 1 performs 200 updates and agent 2 performs 400 updates. This because of the agent-agent network structure as discussed in Sect. 5. As shown in Fig. 1, the algorithm with the Euclidean formulation (23) performs poorly due to a very slow rate of convergence. Our approach, on the other hand, exploits the geometry of the problem and obtains a lower mean squared error (MSE).
6.2 Matrix completion comparisons
For each synthetic example considered here, two matrices \(\mathbf{A} \in \mathbb {R}^{m \times r}\) and \(\mathbf{B} \in \mathbb {R}^{n \times r}\) are generated according to a Gaussian distribution with zero mean and unit standard deviation. The matrix product \(\mathbf{AB} ^\top \) gives a random matrix of rank r (Cai et al. 2010). A fraction of the entries are randomly removed with uniform probability. Noise (sampled from the Gaussian distribution with mean zero and standard deviation \(10^{-6} \)) is added to each entry to construct the training set \(\varOmega \) and \(\mathbf{Y}^\star \). The over-sampling ratio (OS) is the ratio of the number of known entries to the matrix dimension, i.e, \(\mathrm{OS} = |\varOmega |/(mr +nr -r^2)\). We also create a test set by randomly picking a small set of entries from \(\mathbf{AB} ^\top \). The matrices \(\mathbf{Y}^\star _i\) are created by distributing the number of n columns of \(\mathbf{Y}^\star \)equally among the agents. The train and test sets are also partitioned similarly among N agents. All the algorithms are initialized randomly and the regularization parameter \(\lambda \) in (11) is set to \(\lambda = 0\) for all the below considered cases (except in Case 5 below, where \(\lambda = 0.01\)). For cases 1 to 4 below, we fix the number of agents N to 6. In Figs. 2 and 3, however, we show the plots for agents 1 and 2 to make the performance distinctions clearer.
Case 1: effect of \(\rho \). Here, we consider a problem instance of size \(10{,}000 \times 100{,}000\) of rank 5 and OS 6. Two scenarios with \(\rho = 10^3\) and \(\rho = 10^{10}\) are considered. Figure 2a, b show the performance of Stochastic Gossip. Not surprisingly, for \(\rho = 10^{10}\), we only see consensus (the distance between agents 1 and 2 tends to zero). For \(\rho = 10^3\), we observe both a low MSE on the matrix completion problem as well as consensus among the agents.
Case 2: performance of Stochastic Gossip versus Parallel Gossip. We consider Case 1 with \(\rho = 10^3\). Figure 2c, d show the performance of Stochastic Gossip and Parallel Gossip, both of which show a similar behavior on the training set (as well as on the test set, which is not shown here for brevity).
Case 3: ill-conditioned instances. We consider a problem instance of size \(5000 \times 50{,}000\) of rank 5 and impose an exponential decay of singular values with condition number 500 and OS 6. Figure 2e, f show the performance of Stochastic Gossip and its preconditioned variant for \(\rho = 10^3\). During the initial updates, the preconditioned variant aggressively minimizes the completion term of (17), which shows the effect of the preconditioner (21). Eventually, consensus among the agents is achieved.
Case 4: Comparisons with state-of-the-art. We show comparisons with D-LMaFit (Ling et al. 2012; Lin and Ling 2015), the only publicly available decentralized algorithm to the best of our knowledge. It builds upon the batch matrix completion algorithm in (Wen et al. 2012) and is adapted to decentralized updates of the low-rank factors. It requires an inexact dynamic consensus step at every iteration by performing an Euclidean average of low-rank factors (of all the agents). In contrast, our algorithms enforce soft averaging of only two agents at every iteration with the consensus term in (17). We employ a smaller problem instance in this experiment since the D-LMaFit code (supplied by its authors) does not scale to large-scale instances. D-LMaFit is run for 400 iterations, i.e., each agent performs 400 updates. We consider a problem instance of size \(500\times 12{,}000\), rank 5, and OS 6. D-LMaFit is run with the default parameters. For Stochastic Gossip, we set \(\rho = 10^3\). As shown in Fig. 3, Stochastic Gossip quickly outperforms D-LMaFit. Overall, Stochastic Gossip takes fewer number of updates of the agents to reach a high accuracy.
Case 5: comparisons on the Netflix and the MovieLens-10M data-sets. The Netflix dataset (obtained from the code of Recht and Ré (2013)) consists of 100, 480, 507 ratings by 480, 189 users for 17, 770 movies. We perform 10 random 80 / 20-train/test partitions. The training ratings are centered around 0, i.e., the mean rating is subtracted. We split both the train and test data among the agents along the number of users. We run Stochastic Gossip with \(\rho = 10^7\) (set with cross validation) and for \(400(N-1)\) iterations and \(N=\{2,5,10,15,20 \}\) agents. We show the results for rank 10 (the choice is motivated in (Boumal and Absil 2015)). Additionally for Stochastic Gossip, we set the regularization parameter to \(\lambda =0.01\). For comparisons, we show the best test root mean square error (RMSE) score obtained by RTRMC (Boumal and Absil 2011, 2015), which is a fine tuned batch method for solving the matrix completion problem on the Grassmann manifold. RTRMC employs a second-order preconditioned trust-region algorithm. In order to compute the test RMSE for Stochastic Gossip on the full test set (not on the agent-partitioned test sets), we use the (Fréchet) mean subspace of the subspaces obtained by the agents as the final subspace obtained by our algorithm. Table 2 shows the RMSE scores for Stochastic Gossip and RTRMC averaged over ten runs. Table 2 shows that the proposed gossip approach allows to reach a reasonably good solution on the Netflix data with different number of agents (which interact minimally among themselves). It should be noted that as the number of agents increases, the consensus problem (17) becomes challenging. Similarly, consensus of agents at higher ranks is more challenging as we need to learn a larger common subspace. Figure 4 shows the consensus of agents for the case \(N=10\) (shown only three plots for clarity).
We also show the results on the MovieLens-10M dataset of 10, 000, 054 ratings by 71, 567 users for 10, 677 movies (MovieLens 1997). The setup is similar to the earlier Netflix case. We run Stochastic gossip with \(N=\{5,10 \}\) and \(\rho = 10^5\). We show the RMSE scores for different ranks in Table 3.
6.3 Multitask comparisons
In this section, we discuss the numerical results on the low-dimensional multitask feature learning problem (16) on different benchmarks. The regularization parameter \(\lambda \) that is used to solve for \(w_t\) in (16) is set to \(\lambda = 0\) for Case 6 and is set to \(\lambda = 0.1\) for Case 7.
Case 6: synthetic datasets. We consider a toy problem instance with \(T=1000\) tasks. The number of training instance in each task t is between 10 and 50 (\(d_t\) chosen randomly). The input space dimension is \(m =100\). The training instances \(\mathbf{X}_t\) are generated according to the Gaussian distribution with zero mean and unit standard deviation. A 5-dimensional feature subspace \(\mathbf{U}_*\) for the problem instance is generated as a random point on \(\mathbf{U}_* \in {\mathrm {St}({5},{100})}\). The weight vector \(w_t\) for the task t is generated from the Gaussian distribution with zero mean and unit standard deviation. The labels for training instances for task t are computed as \(y_t = \mathbf{X}_t \mathbf{U}_*\mathbf{U}_*{^\top }w_t\). The labels \(y_t\) are subsequently perturbed with a random mean zero Gaussian noise with \(10^{-6}\) standard deviation. The tasks are uniformly divided among \(N=6\) agents and Stochastic Gossip is initialized with \(r=5\) and \(\rho = 10^3\).
Figure 5a shows that all the agents are able to converge to the optimal subspace \(\mathbf{U}_*\).
Case 7: comparisons on multitask benchmarks. We compare the generalization performance with formulation (16) solved by the proposed gossip algorithm against state-of-the-art multitask feature learning algorithms Alt-Min (proposed by Argyriou et al. (2008) for formulation (13)). Alt-Min solves an equivalent convex problem of (13). Conceptually, Alt-Min alternates between the subspace learning step and task weight vector learning step. Alt-Min does optimization over an \(m\times m\)-dimensional space. In contrast, we learn a low-dimensional \(m\times r\) subspace in (16), where \(r\le m\). As discussed below, the experiments show that our algorithms obtain a competitive performance even for values of r where \(r < m\), thereby making the formulation (16) suitable for low-rank multitask feature learning. As a baseline, we also compare against a batch variant for (16) on the Grassmann manifold. In particular, we implement a trust-region algorithm for (16). Similar to Stochastic Gossip, the trust-region method learns a low-dimensional \(m\times r\) subspace.
We compare Stochastic Gossip, Alt-Min, and Trust-region on two real-world multitask benchmark datasets: Parkinsons and School. In the Parkinsons dataset, the goal is to predict the Parkinson’s disease symptom score at different times of 42 patients with \(m = 19\) bio-medical features (Frank and Asuncion; Jawanpuria and Nath 2012; Muandet et al. 2013). A total of 5, 875 observations are available. The symptom score prediction problem for each patient is considered as a task (\(T=42\)). The School dataset consists of 15, 362 students from 139 schools (Goldstein 1991; Evgeniou et al. 2005; Argyriou et al. 2008). The aim is to predict the performance (examination score) of the students from the schools, given the description of the schools and past record of the students. A total of \(m =28\) features are given. The examination score prediction problem for each school is considered as a task (\(T=139\)).
We perform 10 random 80 / 20-train/test partitions. We run Stochastic Gossip with \(\rho = 10^6\), \(N=6\), and for \(200(N-1)\) iterations. Alt-Min and Trust-region are run till the relative change in the objective function (across consecutive iterations) is below the value \(10^{-8}\). Following (Argyriou et al. 2008; Jawanpuria and Nath 2011; Chen et al. 2011), we report the performance of multitask algorithms in terms of normalized mean squared error (NMSE). It is defined as the ratio of the mean squared error (MSE) and the variance of the label vector.
Table 4 shows the NMSE scores (averaged over all T tasks and ten runs) for all the algorithms. The comparisons on benchmark multitask learning datasets show that we are able to obtain smaller NMSE: 0.339 (Parkinsons, \(r=5\)) and 0.761 (School, \(r=3\)). We also obtain these NMSE at a much smaller rank compared to Alt-Min algorithm. The table also shows that Stochastic Gossip obtains NMSE scores close to the trust-region algorithm across different ranks.
Figure 5b shows the NMSE scores obtained by different agents, where certain agents outperform Alt-Min. Overall, the average performance across the agents matches that of the batch Alt-Min algorithm.
7 Conclusion
We have proposed a decentralized Riemannian gossip approach to subspace learning problems. The sub-problems are distributed among a number of agents, which are then required to achieve consensus on the global subspace. Building upon the non-linear gossip framework, we modeled this as minimizing a weighted sum of task solving and consensus terms on the Grassmann manifold. The consensus term exploits the rich geometry of the Grassmann manifold, which allows to propose a novel stochastic gradient algorithm for the problem with simple updates. Experiments on two interesting applications—low-rank matrix completion and multitask feature learning—show the efficacy of the proposed Riemannian gossip approach. Our experiments demonstrate the benefit of exploiting the geometry of the search space that arise in subspace learning problems.
Currently in our gossip framework setup, the agents are tied with a single learning stepsize sequence, which is akin to working with a single universal clock. As future research direction, we intend to work on decoupling the learning rates used by different agents (Colin et al. 2016).
References
Abernethy, J., Bach, F., Evgeniou, T., & Vert, J.-P. (2009). A new approach to collaborative filtering: Operator estimation with spectral regularization. Journal of Machine Learning Research, 10, 803–826.
Absil, P.-A., Mahony, R., & Sepulchre, R. (2008). Optimization algorithms on matrix manifolds. Princeton, NJ: Princeton University Press.
Álvarez, M. A., Rosasco, L., & Lawrence, N. D. (2012). Kernels for vector-valued functions: A review. Foundations and Trends in Machine Learning, 4, 195–266.
Amit, Y., Fink, M., Srebro, N., & Ullman, S. (2007). Uncovering shared structures in multiclass classification. In Proceedings of the 24th international conference on machine learning (pp. 17–24).
Ando, R. K., & Zhang, T. (2005). A framework for learning predictive structures from multiple tasks and unlabeled data. Journal of Machine Learning Research, 6(May), 1817–1853.
Argyriou, A., Evgeniou, T., & Pontil, M. (2008). Convex multi-task feature learning. Machine Learning, 73(3), 243–272.
Balzano, L., Nowak, R., & Recht, B. (2010). Online identification and tracking of subspaces from highly incomplete information. In The 48th annual Allerton conference on communication, control, and computing (Allerton) (pp. 704–711).
Baxter, J. J. (1997). A Bayesian/information theoretic model of learning to learn via multiple task sampling. Machine Learning, 28, 7–39.
Baxter, J. J. (2000). A model of inductive bias learning. Journal of Artificial Intelligence Research, 12, 149–198.
Bishop, C . M. (2006). Pattern recognition and machine learning. Berlin: Springer.
Blot, M., Picard, D., Cord, M., & Thome, N. (2016). Gossip training for deep learning. Technical report, arXiv preprint arXiv:1611.04581.
Bonnabel, S. (2013). Stochastic gradient descent on Riemannian manifolds. IEEE Transactions on Automatic Control, 58(9), 2217–2229.
Boumal, N., & Absil, P. -A. (2011). RTRMC: A Riemannian trust-region method for low-rank matrix completion. In Advances in neural information processing systems 24 (NIPS) (pp. 406–414).
Boumal, N., & Absil, P.-A. (2015). Low-rank matrix completion via preconditioned optimization on the Grassmann manifold. Linear Algebra and its Applications, 475, 200–239.
Boumal, N., Mishra, B., Absil, P.-A., & Sepulchre, R. (2014). Manopt: A Matlab toolbox for optimization on manifolds. Journal of Machine Learning Research, 15, 1455–1459.
Boyd, S., Ghosh, A., Prabhakar, B., & Shah, D. (2006). Randomized gossip algorithms. IEEE Transaction on Information Theory, 52(6), 2508–2530.
Cai, J. F., Candès, E. J., & Shen, Z. (2010). A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 20(4), 1956–1982.
Candès, E. J., & Recht, B. (2009). Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 9(6), 717–772.
Caruana, R. (1997). Multitask learning. Machine Learning, 28(1), 41–75.
Cetingul, H. E., & Vidal, R. (2009). Intrinsic mean shift for clustering on Stiefel and Grassmann manifolds. In IEEE conference on computer vision and pattern recognition (CVPR).
Chen, J., Zhou, J., & Jieping, Y. (2011). Integrating low-rank and group-sparse structures for robust multi-task learning. In ACM SIGKDD international conference on knowledge discovery and data mining (pp. 42–50).
Colin, I., Bellet, A., Salmon, J., & Clémençon, S. (2016). Gossip dual averaging for decentralized optimization of pairwise functions. In International conference on machine learning (ICML) (pp. 1388–1396).
Dai, W., Kerman, E., & Milenkovic, O. (2012). A geometric approach to low-rank matrix completion. IEEE Transactions on Information Theory, 58(1), 237–247.
Dai, W., Milenkovic, O., & Kerman, E. (2011). Subspace evolution and transfer (SET) for low-rank matrix completion. IEEE Transactions on Signal Processing, 59(7), 3120–3132.
Edelman, A., Arias, T. A., & Smith, S. T. (1998). The geometry of algorithms with orthogonality constraints. SIAM Journal on Matrix Analysis and Applications, 20(2), 303–353.
Evgeniou, T., Pontil, M. (2004). Regularized multi-task learning. In ACM SIGKDD international conference on knowledge discovery and data mining (KDD) (pp. 109–117).
Evgeniou, T., Micchelli, C. A., & Pontil, M. (2005). Learning multiple tasks with kernel methods. Journal of Machine Learning Research, 6, 615–637.
Frank, A., & Asuncion, A. UCI machine learning repository. http://archive.ics.uci.edu/ml. Accessed 4 Jan 2019.
Goldstein, H. (1991). Multilevel modelling of survey data. Journal of the Royal Statistical Society. Series D (The Statistician), 40(2), 235–244.
Harandi, M., Hartley, R., Salzmann, M., & Trumpf, J. (2016). Dictionary learning on Grassmann manifolds. In Algorithmic advances in Riemannian geometry and applications (pp. 145–172).
Harandi, M., Salzmann, M., & Hartley, R. (2017). Joint dimensionality reduction and metric learning: A geometric take. In International conference on machine learning (ICML).
Harandi, M., Salzmann, M., & Hartley, R. (2018). Dimensionality reduction on SPD manifolds: The emergence of geometry-aware methods. IEEE Transactions on Pattern Analysis & Machine Intelligence, 40(1), 48–62.
He, J., Balzano, L., & Szlam, A. (2012). Incremental gradient on the Grassmannian for online foreground and background separation in subsampled video. In IEEE conference on computer vision and pattern recognition (CVPR).
Jacob, L., Bach, F., & Vert, J. P. (2008). Clustered multi-task learning: A convex formulation. In Advances in neural information processing systems 21 (NIPS).
Jalali, A., Ravikumar, P., Sanghavi, S., & Ruan, C. (2010). A dirty model for multi-task learning. In Advances in neural information processing systems 23 (NIPS).
Jawanpuria, P., & Nath, J. S. (2011). Multi-task multiple kernel learning. In SIAM international conference on data mining (SDM) (pp. 828–830).
Jawanpuria, P., & Nath, J. S. (2012). A convex feature learning formulation for latent task structure discovery. In International conference on machine learning (ICML) (pp. 1531–1538).
Jin, P. H., Yuan, Q., Iandola, F., & Keutzer, K. (2016). How to scale distributed deep learning? Technical report, arXiv preprint arXiv:1611.04581.
Kang, Z., Grauman, K., & Sha, F. (2011). Learning with whom to share in multi-task feature learning. In International conference on machine learning (ICML) (pp. 521–528).
Kapur, A., Marwah, K., & Alterovitz, G. (2016). Gene expression prediction using low-rank matrix completion. BMC Bioinformatics, 17, 243.
Keshavan, R. H., Montanari, A., & Oh, S. (2009). Low-rank matrix completion with noisy observations: A quantitative comparison. In Annual Allerton conference on communication, control, and computing (Allerton) (pp. 1216–1222).
Keshavan, R. H., Montanari, A., & Oh, S. (2010). Matrix completion from a few entries. IEEE Transactions on Information Theory, 56(6), 2980–2998.
Kumar, A., & Daume, H. (2012). Learning task grouping and overlap in multi-task learning. In International conference on machine learning (ICML).
Lapin, M., Schiele, B., & Hein, M. (2014). Scalable multitask representation learning for scene classification. In Conference on computer vision and pattern recognition.
Ling, Q., Xu, Y., Yin, W., & Wen, Z. (2012). Decentralized low-rank matrix completion. In IEEE international conference on acoustics, speech and signal processing (ICASSP) (pp. 2925–2928).
Lin, A.-Y., & Ling, Q. (2015). Decentralized and privacy-preserving low-rank matrix completion. Journal of the Operations Research Society of China, 3(2), 189–205.
Markovsky, I., & Usevich, K. (2013). Structured low-rank approximation with missing data. SIAM Journal on Matrix Analysis and Applications, 34(2), 814–830.
Meyer, G., Journée, M., Bonnabel, S., & Sepulchre, R. (2009). From subspace learning to distance learning: A geometrical optimization approach. In IEEE/SP 15th workshop on statistical signal processing (pp. 385–388).
Meyer, G., Bonnabel, S., & Sepulchre, R. (2011). Regression on fixed-rank positive semidefinite matrices: A Riemannian approach. Journal of Machine Learning Research, 11, 593–625.
Mishra, B., & Sepulchre, R. (2014). R3MC: A Riemannian three-factor algorithm for low-rank matrix completion. In Proceedings of the 53rd IEEE conference on decision and control (CDC) (pp. 1137–1142).
Mishra, B., Kasai, H., & Saroop, A. (2016). A Riemannian gossip approach to decentralized matrix completion. Technical report, arXiv preprint arXiv:1605.06968, 2016. A shorter version appeared in the 9th NIPS Workshop on Optimization for Machine Learning.
Mishra, B., Meyer, G., Bonnabel, S., & Sepulchre, R. (2014). Fixed-rank matrix factorizations and Riemannian low-rank optimization. Computational Statistics, 29(3–4), 591–621.
MovieLens. MovieLens (1997). http://grouplens.org/datasets/movielens/. Accessed 4 Jan 2019.
Muandet, K., Balduzzi, D., & Schölkopf, B. (2013). Domain generalization via invariant feature representation. In International conference on machine learning (ICML) (pp. 10–18).
Ngo, T. T., & Saad, Y. (2012). Scaled gradients on Grassmann manifolds for matrix completion. In Advances in neural information processing systems 25 (NIPS) (pp. 1421–1429).
Ormándi, R., Hegedűs, I., & Jelasity, M. (2013). Gossip learning with linear models on fully distributed data. Concurrency and Computation: Practice and Experience, 25(4), 556–571.
Recht, B., & Ré, C. (2013). Parallel stochastic gradient algorithms for large-scale matrix completion. Mathematical Programming Computation, 5(2), 201–226.
Rennie, J., & Srebro, N. (2005). Fast maximum margin matrix factorization for collaborative prediction. In International conference on machine learning (ICML) (pp. 713–719).
Sarlette, A., & Sepulchre, R. (2009). Consensus optimization on manifolds. SIAM Journal on Control and Optimization, 48(1), 56–76.
Sato, H., Kasai, H., & Mishra, B. (2017). Riemannian stochastic variance reduced gradient. Technical report, arXiv preprint arXiv:1702.05594.
Shah, D. (2009). Gossip algorithms. Foundations and Trend in Networking, 3(1), 1–125.
Tron, R., Afsari, B., & Vidal, R. (2011). Average consensus on Riemannian manifolds with bounded curvature. In IEEE conference on decision and control and European control conference (CDC-ECC) (pp. 7855–7862).
Tron, R., Afsari, B., & Vidal, R. (2013). Riemannian consensus for manifolds with bounded curvature. IEEE Transactions on Automatic Control, 58(4), 921–934.
Turaga, P., Veeraraghavan, A., & Chellappa, R. (2008). Statistical analysis on Stiefel and Grassmann manifolds with applications in computer vision. In IEEE conference on computer vision and pattern recognition (CVPR).
Wen, Z., Yin, W., & Zhang, Y. (2012). Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Mathematical Programming Computation, 4(4), 333–361.
Yuan, M., & Lin, Y. (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society Series B, 68, 49–67.
Zhang, Y. (2015). Parallel multi-task learning. In IEEE international conference on data mining (ICDM).
Zhang, Y., & Yang, Q. (2017). A survey on multi-task learning. Technical report, arXiv:1707.08114v1.
Zhang, Y., & Yeung, D. Y. (2010). A convex formulation for learning task relationships in multi-task learning. In Uncertainty in artificial intelligence.
Zhang, H., Reddi, S. J., & Sra, S. (2016). Riemannian svrg: Fast stochastic optimization on Riemannian manifolds. In Advances in neural information processing systems (NIPS) (pp. 4592–4600).
Zhang, J., Ghahramani, Z., & Yang, Y. (2008). Flexible latent variable models for multi-task learning. Machine Learning, 73(3), 221–242.
Zhong, L. W., & Kwok, J. T. (2012). Convex multitask learning with flexible task clusters. In International conference on machine learning (ICML).
Zhou, Y., Wilkinson, D., Schreiber, R., & Pan, R. (2008). Large-scale parallel collaborative filtering for the Netflix prize. In International conference on algorithmic aspects in information and management (AAIM) (pp. 337–348).
Acknowledgements
We thank the editor and two anonymous reviewers for carefully checking the paper and providing a number of helpful remarks. Most of the work was done when Bamdev Mishra and Pratik Jawanpuria were with Amazon.com.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Editors: Masashi Sugiyama and Yung-Kyun Noh.
Rights and permissions
About this article
Cite this article
Mishra, B., Kasai, H., Jawanpuria, P. et al. A Riemannian gossip approach to subspace learning on Grassmann manifold. Mach Learn 108, 1783–1803 (2019). https://doi.org/10.1007/s10994-018-05775-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-018-05775-x