Skip to main content
SpringerLink
Log in

Determination of periodic solutions for nonlinear oscillators with fractional powers by He’s modified Lindstedt-Poincaré method

  • Published:
Meccanica Aims and scope Submit manuscript

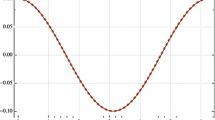
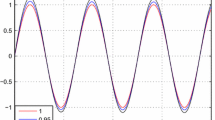
Abstract

He’s modified Lindstedt-Poincaré method is applied to nonlinear oscillatiors with fractional powers. Comparison of the obtained results with exact solutions provides confirmation for the validity of He’s modified Lindstedt-Poincaré method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Brogliato R (1988) Nonsmooth mechanics. Springer, Berlin

    Google Scholar 

  2. Oyedeji KO (2005) An analysis of a nonlinear elastic force van der Pol oscillator equation. J Sound Vib 281:417–422

    Article  MathSciNet  ADS  Google Scholar 

  3. Mickens RE, Oyedeji KO, Rucker SA (2003) Analysis of the simple harmonic oscillator with fractional damping. J Sound Vib 268:839–842

    Article  MathSciNet  ADS  Google Scholar 

  4. Mickens RE (1994) Nonstandard finite difference models of differential equations. World Scientific, Singapore

    MATH  Google Scholar 

  5. Hogan SJ (2003) Relaxation oscillations in a system with a piecewise smooth drag coefficient. J Sound Vib 263:467–471

    Article  MathSciNet  ADS  Google Scholar 

  6. Mickens RE (2003) A combined equivalent linearization and averaging perturbation method for non-linear oscillator equations. J Sound Vib 264:1195–1200

    Article  MathSciNet  ADS  Google Scholar 

  7. Lim CW, Wu BS (2003) Accurate higher-order approximations to frequencies of nonlinear oscillators with fractional powers. J Sound Vib 281:1157–1162

    Article  MathSciNet  ADS  Google Scholar 

  8. He JH (2003) Linearized perturbation technique and its applications to strongly nonlinear oscillators. Comput Math Appl 45:1–8

    Article  MATH  MathSciNet  Google Scholar 

  9. He JH (2006) Non-perturbative methods for strongly nonlinear problems. dissertation.de-verlag im Internet GmbH, Berlin

  10. He JH (2005) Limit cycle and bifurcation of nonlinear problems. Chaos Solitons Fractals 26:827–833

    Article  MATH  Google Scholar 

  11. He JH (2003) Determination of limit cycles for strongly nonlinear oscillators. Phys Rev Lett 90:174301

    Article  ADS  Google Scholar 

  12. Öziş T, Yıldırım A (2007) A note on He’s homotopy perturbation method for van der Pol oscillator with very strong nonlinearity. Chaos Solitons Fractals 34:989–991

    Article  Google Scholar 

  13. Öziş T, Yıldırım A (2007) Determination of limitcycles by a modified straightforward expansion for nonlinear oscillators. Chaos Solitons Fractals 32:445–448

    Article  Google Scholar 

  14. Öziş T, Yıldırım A (2007) Determination of frequency-amplitude relation for duffing-harmonic oscillator by the energy balance method. Comput Math Appl 54:1184–1187

    Article  MATH  MathSciNet  Google Scholar 

  15. Öziş T, Yıldırım A (2007) Determination of periodic solution for a u1/3 force by He’s modified Lindstedt-Poincaré method. J Sound Vib 301:415–419

    Article  ADS  Google Scholar 

  16. Öziş T, Yıldırım A (2007) A study of nonlinear oscillators with u1/3 force by He’s variational iteration method. J Sound Vib 306:372–376

    Article  ADS  Google Scholar 

  17. He JH (1999) Analytical solution of a nonlinear oscillator by the linearized perturbation technique. Commun Nonlinear Sci Numer Simul 4:109–113

    Article  MATH  MathSciNet  ADS  Google Scholar 

  18. He JH (1999) Modified straightforward expansion. Meccanica 34:287–289

    Article  MATH  Google Scholar 

  19. Mickens RE (2001) Oscillations in an x 4/3 potential. J Sound Vib 246:375–378

    Article  MathSciNet  ADS  Google Scholar 

  20. He JH (2002) Modified Lindstedt-Poincaré methods for some strongly non-linear oscillations, part I: expansion of a constant. Int J Non-Linear Mech 37:309–314

    Article  MATH  Google Scholar 

  21. Wang SQ, He JH (2008) Nonlinear oscillator with discontinuity by parameter-expansion method. Chaos Solitons Fractals 35:688–691

    Article  MATH  MathSciNet  Google Scholar 

  22. Shou DH, He JH (2007) Application of parameter-expanding method to strongly nonlinear oscillators. Int J Nonlinear Sci Numer Simul 8:121–124

    Google Scholar 

  23. Zengin FO, Kaya MO, Demirbag SA (2008) Application of parameter-expansion method to nonlinear oscillators with discontinuities. Int J Nonlinear Sci Numer Simul 9:267–270

    Google Scholar 

  24. Zhang LN, Xu L (2007) Determination of the limit cycle by He’s parameter-expansion for oscillators in a u(3)/(1+u(2)) potential. Z Naturforsch A, J Phys Sci 62:396–398

    Google Scholar 

  25. Xu L (2007) Application of He’s parameter-expansion method to an oscillation of a mass attached to a stretched elastic wire. Phys Lett A 368:259–262

    Article  ADS  Google Scholar 

  26. Xu L (2007) Determination of limit cycle by He’s parameter-expanding method for strongly nonlinear oscillators. J Sound Vib 302:178–184

    Article  ADS  Google Scholar 

  27. Nayfeh AH (1973) Perturbation methods. Wiley-Interscience, New York

    MATH  Google Scholar 

  28. Mickens RE (1996) Oscillations in planar dynamics systems. World Scientific, Singapore

    Google Scholar 

  29. Jordan DW, Smith P (1987) Nonlinear ordinary differential equations. Clarendon, Oxford

    MATH  Google Scholar 

  30. Hagedorn P (1981) Nonlinear oscillations (translated by Wolfram Stadler). Clarendon, Oxford

    Google Scholar 

  31. He JH (2006) Some asymptotic methods for strongly nonlinear equations. Int J Mod Phys B 20:1141–1199

    Article  MATH  ADS  Google Scholar 

  32. He JH (2002) Recent developments in asymptotic methods for nonlinear ordinary equations. Int J Comput Numer Anal Appl 2:127–190

    MATH  MathSciNet  Google Scholar 

  33. Gottlieb HPW (2003) Frequencies of oscillators with fractional-power nonlinearities. J Sound Vib 261:557–566

    Article  MathSciNet  ADS  Google Scholar 

  34. Waluya SB, van Horssen WT (2003) On the periodic solutions of a generalized non-linear Van der Pol oscillator. J Sound Vib 268:209–215

    Article  ADS  Google Scholar 

  35. Wu B, Li P (2001) A method for obtaining approximate analytic periods for a class of nonlinear oscillators. Meccanica 36:167–176

    Article  MATH  Google Scholar 

  36. He JH (2000) A modified perturbation technique depending upon an artificial parameter. Meccanica 35:299–311

    Article  MATH  MathSciNet  Google Scholar 

  37. Marinca V, Herişanu N, Bota C (2008) Application of the variational iteration method to some nonlinear one-dimensional oscillations. Meccanica 43:75–79

    Article  MATH  Google Scholar 

  38. Villaggio P (2008) Small perturbations and large self-quotations. Meccanica 43:81–83

    Article  MATH  Google Scholar 

  39. Spanos PD, Di Paola M, Failla G (2002) A Galerkin approach for power spectrum determination of nonlinear oscillators. Meccanica 37:51–65

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Science Faculty, Ege University, 35100, Bornova-İzmir, Turkey

    Ahmet Yildirim

Authors
  1. Ahmet Yildirim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmet Yildirim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yildirim, A. Determination of periodic solutions for nonlinear oscillators with fractional powers by He’s modified Lindstedt-Poincaré method. Meccanica 45, 1–6 (2010). https://doi.org/10.1007/s11012-009-9212-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-009-9212-4

Keywords

Search

Navigation