Peak Oil: Testing Hubbert’s Curve via Theoretical Modeling

Abstract

A theoretical model of conventional oil production has been developed. The model does not assume Hubbert’s bell curve, an asymmetric bell curve, or a reserve-to-production ratio method is correct, and does not use oil production data as an input. The theoretical model is in close agreement with actual production data until the 1979 oil crisis, with an R ² value of greater than 0.98. Whilst the theoretical model indicates that an ideal production curve is slightly asymmetric, which differs from Hubbert’s curve, the ideal model compares well with the Hubbert model, with R ² values in excess of 0.95. Amending the theoretical model to take into account the 1979 oil crisis, and assuming the ultimately recoverable resources are in the range of 2–3 trillion barrels, the amended model predicts conventional oil production to peak between 2010 and 2025. The amended model, for the case when the ultimately recoverable resources is 2.2 trillion barrels, indicates that oil production peaks in 2013.

Introduction

There is considerable debate on when and how steeply oil production will peak, with a range of estimates from 2004 to 2047 (e.g., Aleklett, 2004; Deffeyes, 2002; Bakhtiari, 2004; Mohr and Evans, 2007; Wells, 2005a, 2005b; Wood, Long, and Morehouse, 2004). The considerable range in peak oil estimates is due to two main factors. The first factor is uncertainty in the conventional oil ultimately recoverable resources (URR), with Bauquis (2003) indicating that estimates typically range from 2 to 3 trillion barrels. The second factor is the different methods for modeling conventional oil production. Oil production is modeled in three distinct ways. Wells (2005a, 2005b), Mohr and Evans (2007), and Deffeyes (2002) used a bell (or Hubbert) curve to model oil production. The second method, used by Aleklett (2004) and Bakhtiari (2004), was a graphical model with limited data as to how the model is created. The last method, used by Wood, Long, and Morehouse (2004), assumed oil production declines with a reserves-to-production (R/P) ratio of 10. The different models create very different production profiles, and hence a wide range of predictions, which ultimately confuse the wider community. Rather than assume a production curve, and attempt to justify its use, this article will endeavor to generate a model based on theory. With the theory explained, we will then determine what the oil production profile looks like.

Review of Literature

Before explaining how the current model works, it is important to look carefully at the theoretical models developed by Reynolds (1999) and Bardi (2005). Reynolds (1999) explains qualitatively how oil discoveries are comparable to the Mayflower problem. Bardi (2005) using this technique explains the model mathematically as:

$$ p(t) = k(t)\frac{URR-C_{\rm d}(t)}{URR}, $$

(1)

where p(t) is the expected discovery percentage, URR is the Ultimate Recoverable Resources (TL), C _d(t) is the cumulative discoveries (TL), and k(t) is the technology function, which Bardi (2005) defines as “a simple linear function of the amount of previously found [oil reserves] that starts at 1 and increases proportionally to the total amount of found [oil reserves].” The models of Reynolds (1999) and Bardi (2005) are based on a simplified scenario with Robinson Crusoe digging for buried hardtacks (food).

The work done by Brandt (2007) is statistical. Brandt (2007) obtained production data for many places of various sizes. The result from Brandt’s (2007) research is that the rate difference, Δr, is slightly positive with a median value of 0.05 year⁻¹, which implies that on average the rate of increase is slightly larger than the rate of decrease (see Appendix A).

Model

The model of oil production is determined in several subsections. In the “Discovery” subsection, the amount of oil found in a given year will be determined. It will then be assumed that the amount of oil found each year is located in a single reservoir. The “Reservoir Production” subsection will model oil production in a reservoir by estimating the number of wells in operation and estimating the oil production per well. The world production model is then determined by adding up the oil production of all the reservoirs.

Discoveries

We will assume that finding oil is equivalent to the Mayflower problem, hence the expected discovery percentage function will be determined by Equation (1) (Bardi, 2005). Now the technology function k(t) must be between 0 and 1, in order for the expected discovery percentage to remain bounded between 0 and 1. It is worth noting that some optimists such as Linden (1998) believe that technology makes “marginal hydrocarbon resources” economic. It is also reasonable to assume that the technology function is non-decreasing. Given these constraints we will assume the technology function k(t) as:

$$ k(t) = \left[\hbox{tanh } \left(b_{\rm t}\left(t-t_{\rm t}\right)\right)+1\right]/2, $$

where b _t and t _t are constants with units (year⁻¹) and (year), respectively. Hence the expected discovery percentage function is:

$$ p(t)= \left[\hbox{tanh}\ \left(b_{\rm t}\left(t-t_{\rm t}\right)\right)+1\right] \frac{URR-C_{\rm d}(t)}{2URR}. $$

(2)

Initially, the expected discovery percentage is low as our knowledge is limited. As time goes by, the expected discovery percentage increases as our knowledge grows, whilst the amount of oil discovered is still small (relative to the URR). Eventually we have good knowledge of where the oil is to be found, but the amount of oil left to be discovered is small (relative to the URR), hence the expected discovery percentage is low. Let C _d(t) denote the cumulative discoveries of oil made at the beginning of year t. Now, the amount of oil found in year t equals the expected discovery percentage times the amount of oil left to be found in year t,

$$ C_{\rm d}(t+1)-C_{\rm d}(t) = p(t)(URR-C_{\rm d}(t)). $$

(3)

Now since the expected discovery percentage function p(t) is continuous, we can express Equation (3) in the continuous form as

$$ \frac{dC_{\rm d}(t)}{dt}= p(t) (URR-C_{\rm d}(t)). $$

Substituting Equation (2) for the expected discovery percentage function p(t) we obtain

$$ \frac{dC_{\rm d}(t)}{dt}=\left[\hbox{tanh } \left(b_{\rm t}\left(t-t_{\rm t}\right)\right)+1\right] \frac{(URR-C_{\rm d}(t))^2}{2 URR}. $$

(4)

With the trivial assumption that initially C _d(0) = 0, Equation (4) is solved to obtain

$$ C_{\rm d}(t)= URR - \frac{2 b_{\rm t} URR }{2 b_{\rm t} +t b_{\rm t} + \hbox{ln} \left(\frac{{\rm cosh} (b_{\rm t}(t-t_{\rm t}))}{{\rm cosh} (b_{\rm t} t_{\rm t})}\right)}. $$

(5)

Let y _d(t) denote the yearly discoveries (TL/year), dC _d(t)/dt, then by differentiating Equation (5) we obtain,

$$ y_{\rm d}(t) = \frac{2b_{\rm t}^2URR\left(1+{\rm tanh } (b_{\rm t}(t-t_{\rm t}))\right)} {\left(2b_{\rm t}+tb_{\rm t}+\hbox{ln}\left(\frac{{\rm cosh}(b_{\rm t}(t-t_{\rm t}))} {{\rm cosh}(b_{\rm t}t_{\rm t})}\right)\right)^2}. $$

(6)

Let URR _l denote the size of the lth reservoir (TL), which is assumed to be found in the year t _l . Now since we assume that the amount of oil found each year is found in a single reservoir, we have

$$ URR_l=y_{\rm d}(t_l). $$

Reservoir Production

To determine the production curve from a reservoir, we will assume that oil production is related to the number of wells drilled, and the production per well. Let $C_{{\rm p}_{l}}(t)$ denote the cumulative production from the lth reservoir (TL). Let w _l (t) denote the number of wells in operation at time t. The function w _l (t), will be defined by

$$ w_{l}(t) = w_{l_{\rm T}} +(1-w_{l_{\rm T}})e^{-k_{w_{l}}\left(\frac{C_{{\rm p}_{l}}(t)}{URR_{l}}\right)}, \quad t\geq t_l $$

(7)

where $k_{w_{l}}$ is a proportionality constant and $w_{l_{\rm T}}$ is the total number of wells in operation assuming $C_{{\rm p}_{l}}(t)$ increases to infinity. The boundary condition $C_{{\rm p}_{l}}(t_l)=0$ implies w _l (t _l ) = 1, hence initially there is only one well built. As cumulative production increases, the number of wells exponentially changes from 1 well to $w_{l_{\rm T}}$ wells. The total number of wells built is not $w_{l_{\rm T}}$ but $w_{l_{{\rm T}_{\rm act}}}$ which is defined as

$$ w_{l_{{\rm T}_{\rm act}}} = \left\lceil w_{l_{\rm T}}-(w_{l_{\rm T}}-1)e^{-k_{w_{l}}} \right\rceil . $$

Let’s assume that every well in the lth reservoir extracts a total of $URR_{l}/w_{l_{{\rm T}_{\rm act}}}$ (TL) of oil. Let the ith well start production in the $t_{l_i}\hbox{th}$ year, where $t_{l_i}$ is the year such that $\left\lceil w_{l}(t_{l_i}-1)\right\rceil < i \leq \left\lceil w_{l}(t_{l_i})\right\rceil$ (initially $t_{l_1}=t_l).$ Let $C_{{\rm p}_{l_{i}}}$ denote the cumulative production from well i. Production for an individual well is assumed to be the idealized well explained in Arps (1945). In this case, there is no water injection, and oil production in the ith well, $P_{l_{i}},$ is proportional to the pressure in the ith well, $Pr_{{l_i}}.$ Further the pressure in the well is proportional to the remaining amount of oil in the ith well, $(URR_{l}/w_{l_{{\rm T}_{\rm act}}}-C_{p_{l_{i}}}(t-t_{l_i})),$ as shown in Equations (8) and (9) (Arps, 1945):

$$ P_{l_i}(t) = k_{1_{l_i}} Pr_{l_i}(t), $$

(8)

$$ Pr_{l_i}(t) = k_{2_{l_i}} \left( URR_{l}/w_{l_{{\rm T}_{\rm act}}}-C_{p_{l_{i}}}(t)\right). $$

(9)

$k_{1_{l_i}}$ and $k_{2_{l_i}}$ are proportionality constants. Equations (8) and (9) can be combined to obtain

$$ P_{l_i}(t) = k_{1_{l_i}}k_{2_{l_i}} \left(URR_{l}/w_{l_{{\rm T}_{\rm act}}}-C_{{\rm p}_{l_{i}}}(t)\right). $$

Now, $dC_{{\rm p}_{l_{i}}}(t)/dt = P_{l_i}(t),$ hence

$$ \frac{dC_{{\rm p}_{l_{i}}}(t)}{dt} = k_{{\rm p}_{l_i}} \left(URR_{l}/w_{l_{{\rm T}_{\rm act}}}-C_{{\rm p}_{l_{i}}}(t)\right), $$

(10)

where $k_{{\rm p}_{l_i}}=k_{1_{l_i}}k_{2_{l_i}},$ and $C_{{\rm p}_{l_{i}}}(t_{l_i})=0.$ Now Equation (10) is solved to obtain

$$ C_{{\rm p}_{l_{i}}}(t) = \frac{URR_{l}}{w_{l_{{\rm T}_{\rm act}}}}\left[1-e^{-k_{{\rm p}_{l_i}}(t-t_{l_i})}\right], $$

and differentiating obtains the production curve

$$ P_{l_i}(t) = k_{{\rm p}_{l_i}}\frac{URR_{l}}{w_{l_{{\rm T}_{\rm act}}}}e^{-k_{{\rm p}_{l_i}}(t-t_{l_i})}. $$

Let the initial production of the ith well, in the lth reservoir be $P_{0_{l_i}},\,\, (P_{l_i}(t_{l_i})=P_{0_{l_i}} \, \forall i)$ then the production curve for the ith well is (Arps, 1945)

$$ P_{l_i}(t) = P_{0_{l_i}} e^{-P_{0_{l_i}}w_{l_{{\rm T}_{\rm act}}}(t-t_{l_i})/URR_{l}}. $$

Hence the cumulative production for the lth reservoir, $C_{{\rm p}_{l}}(t),$ is determined iteratively by

$$ C_{{\rm p}_{l}}(t+1) =C_{{\rm p}_{l}}(t)+ \sum_{i=1}^{\left\lceil w_{l}(t)\right\rceil}\left(\frac{P_{l_i}(t)+P_{l_i}(t+1)}{2}\right), $$

(11)

with the initial condition $C_{{\rm p}_{l}}(t_l)=0.$ The world’s cumulative production, C _p(t), is the sum of the cumulative production of the reservoirs,

$$ C_{\rm p}(t) = \sum_{l} C_{{\rm p}_{l}}(t) $$

For convenience we will assume that all wells in all reservoirs have the same initial production, P ₀, that is $P_0=P_{0_{l_i}},$ and $k_{\rm w}=k_{{\rm w}_{l}}.$

Results and Discussion

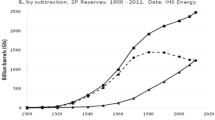
Bauquis (2003) indicates that URR estimates for conventional oil have remained constant at between 2 and 3 trillion barrels (318–477 TL) for the time period of 1973–2000. A pessimistic case will assume that the URR is 318 TL (2 trillion barrels); the optimistic case will assume the URR to be 477 TL (3 trillion barrels). A third, ideal case is also made where the URR is determined from the actual backdated discoveries data from Wells (2005b). We have several constants which need to be defined. For the discovery model we have URR, t _t and b _t, for the number of wells model, k _w, and $w_{l_{\rm T}}$ and for the production of a well we need P ₀. The variables for the discovery model were calculated by fitting the model to the actual data from Wells (2005b) using the coefficient of determination, R ² (for more details see Appendix B). The cumulative discoveries as a function of time is shown in Fig. 1.

Figure 1

The modeled cumulative discoveries as a function of time (the year 1860 is assumed as the start year t = 0.)

In order to determine valid estimates for k _w, $w_{l_{\rm T}},$ and P ₀, it was necessary to find some data. The best literature found to date is from EIA (2007), which has incomplete well and production data for all U.S. states. By analyzing the EIA (2007) data, we assumed P ₀ = 18.3 ML/year, k _w = 10.7 and $w_{l_{\rm T}}=0.072 URR_{l}/P_0 ,$ respectively (for more details see Appendix C). With the constants determined, the world model is shown in Fig. 2; and compared to actual production data from BP (2006), DeGolyer and MacNaughton Inc. (2006), CAPP (2006), Williams (2003), and Moritis (2005).

Figure 2

The production model compared to the actual data

The resulting model of production matches the production data with a reasonable precision up to the 1979 oil crisis (year 119 in Fig. 2) with an R ² value in all three cases of greater than 0.98. The theoretical models when fitted to the asymmetric exponential model, have a slightly positive rate difference of Δr ≈ 0.02 year⁻¹, which agrees with the statistical analysis of Brandt (2007), who indicated a median rate difference of Δr = 0.05 year⁻¹ (Appendix A). The theoretical models are approximately symmetrical and have R ² values of greater than 0.95 when compared to Hubbert curves with the same URR fitted to production data prior to 1979, with the ideal case compared to the Hubbert curve having an R ² value of 0.995.

The theoretical model was amended by use of a technique in Mohr and Evans (2007) to account for the 1979 oil crisis. The method in Mohr and Evans (2007) has four key components. First, the original theoretical curve is used to model oil production prior to the anomaly (1979 oil crisis). Second, simple linear or lower-order polynomials are fitted to the production data from the anomaly to the present day. Third, a polynomial is used to extend the recent production trend, and smoothly rejoin the original theoretical model in the future. Fourth, the model returns to the original theoretical model, shifted a certain distance into the future to ensure the area under the graph (URR) is the same. Modifying the theoretical production curve using the method in Mohr and Evans (2007) allowed for the 1979 oil crisis to be factored (Appendix D). The amended model, Fig. 3, indicates that the ideal case will peak in 2013, at 13.3 GL/d (83.5 mb/d). The optimistic case peaks in 2025 at 14.1 GL/d (88.8 mb/d), and the pessimistic case peaks in 2010, at 13 GL/d (81.8 mb/d).

Figure 3

Results of the modified model compared to the actual production data

Whilst the theoretical model matches the data with reasonable accuracy up to the 1979 oil crisis, R ² > 0.98, there are several gross simplifications. The assumption that P ₀ and k _w are constants for all wells and reservoirs is too simplistic. Also, instead of modeling four U.S. states and using these values to estimate P ₀ and k _w, it would be better to use a set of reservoir data, to determine the average P ₀ and k _w for each reservoir. Unfortunately, such data are not found.

Conclusion

A model has been developed to model oil production using simple theoretical logic. The model accurately replicates the actual discovery and production trends, whilst remaining theoretical. The model produces a bell curve, which is slightly asymmetric with a slightly larger rate of increase compared to the rate of decrease (Δr ≈ 0.02 year⁻¹). The model validates Hubbert’s empirical model which indicates that oil production follows a symmetric bell curve. The amended theoretical model indicates that conventional oil production will peak somewhere between 2010 and 2025, with the ideal case peaking in 2013, at 13.3 GL/d (83.5 mb/d).

Appendices

Appendix A: The Rate Difference

The rate difference, Δr, as defined by (Brandt, 2007) is

$$ \Updelta r = r_{\rm inc}-r_{\rm dec}, $$

where the rate of increase r _inc and rate of decrease r _dec are determined by fitting Equation (A.1) to the production data (Brandt, 2007).

$$ P^{\prime}(t) = \left\{ \begin{array}{lll} e^{r_{{\rm inc}}(t-T_{\rm start})} & \hbox{if} & t \leq T_{\rm peak} \\ P^{\prime}(T_{\rm peak})e^{-r_{\rm dec}(t-T_{\rm peak})} & \hbox{if} & t > T_{\rm peak} \end{array} \right. $$

(A.1)

where P′(t) is production in (barrels/year) and T _peak is the year the production peaks (year) and r _inc and r _dec are the rate constants (year⁻¹) and T _start is the year production was 1 barrel a year Brandt (2007). In calculating the rate difference of the theoretical model equation (A.1) was altered to

$$ P^{\prime}(t) = \left\{ \begin{array}{lll} P(40)e^{r_{{\rm inc}}(t-40)} & \hbox{if} & t \leq T_{\rm peak} \\ P^{\prime}(T_{\rm peak})e^{-r_{\rm dec}(t-T_{\rm peak})} & \hbox{if} & t > T_{\rm peak} \end{array} \right. $$

(A.2)

where P(40) is the production of oil estimated by the theoretical model in the year 1900. Using Equation (A.2) the rate difference for the pessimistic case was 0.0184 (years⁻¹), optimistic case was 0.0179 (years⁻¹), and the ideal case was 0.0217 (years⁻¹).

Appendix B: Coefficient of Determination

The coefficient of determination, R ², was used to measure the accuracy of the discovery model to the data.

$$ R^2=\sum_{n}\frac{[y_f(n)-\bar{y}_{a}]^2-[y_f(n)-y_a(n)]^2} {[y_f(n)-\bar{y}_{a}]^2} $$

For the pessimistic case URR = 2 trillion barrels and for the optimistic case URR = 3 trillion barrels. For the ideal case, the URR was a variable. The best fit was found by varying b _t, t _t (and URR for ideal case) to obtain the highest R ² value. The constants are shown in Table B.1. The actual data for the pessimistic and optimistic cases was truncated to the year 1966, as the optimists claim that oil reserves found in the past will grow.

Table B.1 The URR, b _t, and t _t for the 3 Cases

Appendix C: Determining the Constants

The method to determine valid estimates for the constants $k_{\rm w},\, w_{l_{\rm T}},$ and P ₀ in the reservoir production model is given in this section. The best data found is unfortunately state based rather than reservoir based data from EIA (2007). The production model was used with several cycles to model the production as a function of time, and the number of wells as a function of cumulative production for various states as shown in Figs. C.1–C.4.

Figure C.1

(a) The number of wells as a function of cumulative production for Alaska and (b) Production as a function of time for Alaska

Figure C.2

(a) The number of wells as a function of cumulative production for Alabama and (b) Production as a function of time for Alabama

Figure C.3

(a) The number of wells as a function of cumulative production for Nevada and (b) Production as a function of time for Nevada

Figure C.4

(a) The number of wells as a function of cumulative production for South Dakota and (b) Production as a function of time for South Dakota

Note our model assumes that no wells are shut down, and instead exponentially decay and although are still on-line, are in reality producing no significant quantity of oil. This is the reason for the poor fit of the well model for Nevada and South Dakota. Now observe that there is only one sensible option for the $w_{l_{\rm T}}$ constants, since these values need to match the actual total wells. The k _w values and P ₀ values determine the rate of increase in the wells model and are determined by trial and error so that the wells model and production model fit the data as accurately as possible. Whilst the values used produce reasonably accurate results, we need to check that the initial production values P ₀ correspond to the actual initial production. Unfortunately the initial production for all the wells is not known; however, the number of wells as a function of size and time is known (EIA 2007) and the model’s predictions were compared with the actual data for the four states, as shown in Figs. C.5–C.8 (Note that the size of the wells from EIA, 2007 is explained in Table C.1).

Table C.1 The Size of Wells from EIA (2007)

Figure C.5

The number of wells as a function of size and time for Alaska. (a) Actual and (b) Model

Figure C.6

The number of wells as a function of size and time for Alabama. (a) Actual and (b) Model

Figure C.7

The number of wells as a function of size and time for Nevada. (a) Actual and (b) Model

Figure C.8

The number of wells as a function of size and time for South Dakota. (a) Actual and (b) Model

The Figs. C.5–C.8 indicate a reasonable fit and hence the initial well productions P ₀ can be assumed to be reasonable estimates. The constants k _w, P ₀, and $w_{l_{\rm T}}$ used in the state models are shown in Table C.2.

Table C.2 The Constants for Various States

Now if we ignore the outlier of 32 for South Dakota, the average for k _w is 10.7 and this value is assumed to be constant in the world model; including the outlier the average becomes 12. By plotting w _T vs. URR _l /P ₀ we obtained the linear relation $w_{l_{\rm T}} = 0.072 URR_{l}/P_0$ which is shown in Fig. C.9. The linear relationship is expected, as increasing the size of the reservoir would increase the total number of wells needed. Equally if we have two reservoirs of the same size we could either have a small number of wells with a large initial production P ₀ or a large number of wells with a small initial production P ₀. Hence the linear relationship between $w_{l_{\rm T}}$ and URR _l /P ₀ was expected.

Figure C.9

$w_{l_{\rm T}}$ versus URR _l /P ₀

The value for P ₀ appears to have a great deal of variability. However, by analyzing the other U.S. state wells sizes from EIA (2007), we observe that Alaska along with Federal Pacific and Federal Gulf, have abnormally large wells compared to the rest of the U.S., we hence considered the Alaskan well production data as an outlier and ignored the data. Taking the initial production from Nevada, South Dakota, and Alabama, we obtain an average of 18.3 ML/year, which places it in category 16 in the EIA sizes. Hence we assumed that the values of the constants were P ₀ = 18.3 ML/year, k _w = 10.7, and $w_{l_{\rm T}}=0.072 URR_{l}/P_0.$

Appendix D: Amended Model

The amended model $C_{{\rm p}_{\rm mod}}(t)$ is determined from the method explained in Mohr and Evans (2007), and formally is:

$$ C_{{\rm p}_{\rm mod}}(t)=\left\{ \begin{array}{lll} C_{\rm p}(t) & \hbox{if} & t\leq 118 \\ f_1(t) & \hbox{if} & 118 < t\leq 123 \\ f_2(t) & \hbox{if} & 123 < t \leq 129 \\ f_3(t) & \hbox{if} & 129 < t\leq 145 \\ f_4(t) & \hbox{if} & 145 < t\leq t_2 \\ C_{\rm p}(t+(t_1-t_2)) & \hbox{if} & t_2 < t \end{array} \right. . $$

Now f ₁(t), f ₂(t), and f ₃(t) are small polynomials fitted to the production data using least squares method, and formally are:

$$ \begin{aligned}f_1(t) & = -0.82t+121.7 \\ f_2(t)& =0.43t-32.3\\ f_3(t)& = 0.007t^2-1.6t+109.5 \end{aligned} $$

the f ₄(t) is a 3rd degree polynomial. The polynomial was determined by the literature method explained generally in Mohr and Evans (2007). Specifically f ₄(t) is the 3rd degree polynomial such that the following equations are solved:

$$ \begin{aligned} f_4(145) &=p(145)\\ f'_4(145) & = p'(145)\\ f''_4(145) & = p''(145)\\ f_4(t_2) &=C_{\rm p}(t_1)\\ f'_4(t_2) &=C'_{\rm p}(t_1)\\ \int\limits_{t_0}^{t_1}{C_{\rm p}(t)dt} &=\int\limits_{145}^{t_2}{p(t)dt}. \end{aligned} $$

where t ₀ ≈ 138 and p(t) is a polynomial to replicate the long-term historic trend and is p(t) = −0.004t ² + 1.5t−104.6. With the list of equations solved, we obtain t ₁ = 153.5, t ₂ = 162, and f ₄(t) = −0.0012t ³ + 0.51t ² − 73.4t + 3515.6 for the ideal case. For the pessimistic case it was t ₁ = 147.2, t ₂ = 153.6, and f ₄(t) = −0.0041t ³ + 1.77t ² − 256.2t + 12353.8. t ₁ = 177.8, t ₂ = 196.4, and f ₄(t) = −0.00009t ³ + 0.036t ² − 4.3t + 178.8 for the optimistic case.