Skip to main content
SpringerLink
Log in

An extended Korteweg–de Vries equation: multi-soliton solutions and conservation laws

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

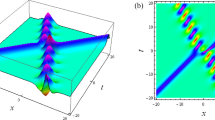
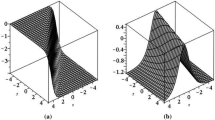
In this paper, we consider an extended KdV equation, which arises in the analysis of several problems in soliton theory. First, we converted the underlying equation into the Hirota bilinear form. Then, using the novel test function method, abundant multi-soliton solutions were obtained. Second, we have performed some distinct methods to extended KdV equation for getting some exact wave solutions. In this regard, Kudryashov’s simplest equation methods were examined. Third, the local conservation laws are deduced by multiplier/homotopy methods. Finally, the graphical simulations of the exact solutions are depicted.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering Transform. Cambridge University Press, Cambridge (1990)

    MATH  Google Scholar 

  2. Vakhnenko, V.O., Parkes, E.J., Morrison, A.J.: A Bäcklund transformation and the inverse scattering transform method for the generalised Vakhnenko equation. Chaos Solitons Fractals 17(4), 683 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  3. Hirota, R.: Direct method of finding exact solutions of nonlinear evolution equations. In: Bullough, R., Caudrey, P. (eds.) Backlund Transformations. Springer, Berlin (1980)

    Google Scholar 

  4. Malfliet, W., Hereman, W.: The tanh method: I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 54(6), 563–568 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  5. Wazwaz, A.M.: The tanh method for travelling wave solutions of nonlinear equations. Appl. Math. Comput. 154(3), 713 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Ma, W.X., Tingwen, H., Yi, Z.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82(6), 6065003 (2010)

    Article  Google Scholar 

  7. Ma, W.X., Yuncheng, Y.: Solving the Korteweg–de Vries equation by its bilinear form: Wronskian solutions. Trans. Am. Math. Soc. 357(5), 1753–1778 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. He, J.H., Wu, X.H.: Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 30(3), 700–708 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  9. Feng, Z.: The first-integral method to study the Burgers–Korteweg–de Vries equation. J. Phys. A Math. Gen. 35(2), 343 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ma, W.X.: Bilinear equations, Bell polynomials and linear superposition principle. Journal of Physics: Conference Series. vol. 411 No. 1. IOP Publishing (2013)

  11. Marchant, T.R.: Solitary wave interaction for the extended BBM equation. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 456, No. 1994, pp. 433–453. The Royal Society (2000)

  12. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  13. Wazwaz, A.M.: The simplified Hirota’s method for studying three extended higher-order KdV-type equations. J. Ocean Eng. Sci. 1, 181–185 (2016)

    Article  Google Scholar 

  14. Seadawy, A.R.: Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comput. Math. Appl. 70, 345–352 (2015)

    Article  MathSciNet  Google Scholar 

  15. Miao, Q., Wang, Y., Chen, Y., Yang, Y.: PDEBellII: A Maple package for finding bilinear forms, bilinear Bcklund transformations, Lax pairs and conservation laws of the KdV-type equations. Comput. Phys. Commun. 185(1), 357–367 (2014)

    Article  MATH  Google Scholar 

  16. Hirota, R.: The Direct Method in Soliton Theory, vol. 155. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  17. Singh, M., Gupta, R.K.: Bäcklund transformations, Lax system, conservation laws and multisoliton solutions for Jimbo–Miwa equation with Bell-polynomials. Commun. Nonlinear Sci. Numer. Simul. 37, 362–373 (2016)

    Article  MathSciNet  Google Scholar 

  18. Singh, M., Gupta, R.K.: Exact solutions for nonlinear evolution equations using novel test function. Nonlinear Dyn. 86(2), 1171–1182 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kudryashov, N.A.: Exact solitary waves of the Fisher equation. Phys. Lett. A 342, 99–106 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kudryashov, N.A.: Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 24, 1217–1231 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kudryashov, N.A.: One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 17, 2248–2253 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  22. Adem, A.R., Khalique, C.M.: Symbolic computation of conservation laws and exact solutions of a coupled variable-coefficient modified Korteweg–de Vries system. Comput. Math. Math. Phys. 56(4), 650–660 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Vitanov, N.K.: Application of simplest equations of Bernoulli and Riccati kind for obtaining exact traveling wave solutions for a class of PDEs with polynomial nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 15, 2050–2060 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yu, J., Wang, D.S., Sun, Y., Suping, Wu: Modified method of simplest equation for obtaining exact solutions of the Zakharov–Kuznetsov equation, the modified Zakharov–Kuznetsov equation, and their generalized forms. Nonlinear Dyn. 85, 2449–2465 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  25. Adem, A.R., Khalique, C.M.: Exact solutions and conservation laws of a two-dimensional integrable generalization of the Kaup–Kupershmidt equation. J. Appl. Math. 647313, 6 (2013)

    MathSciNet  MATH  Google Scholar 

  26. Cheviakov, A.F.: GeM software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 176, 48–61 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  27. Cheviakov, A.F.: Symbolic computation of local symmetries of nonlinear and linear partial and ordinary differential equations. Math. Comput. Sci. 4, 203–222 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  28. Adem, A.R., Khalique, C.M.: Conserved quantities and solutions of a (2+ 1)-dimensional Haragus-Courcelle–Il’ichev model. Comput. Math. Appl. 71(5), 1129–1136 (2016)

    Article  MathSciNet  Google Scholar 

  29. Moleleki, L.D., Muatjetjeja, B., Adem, A.R.: Solutions and conservation laws of a (3+1)-dimensional Zakharov–Kuznetsov equation. Nonlinear Dyn. 87, 2187 (2017)

    Article  MathSciNet  Google Scholar 

  30. Triki, H., Ak, T., Ekici, M., Sonmezoglu, A., Mirzazadeh, M., Kara, A.H., Aydemir, T.: Some new exact wave solutions and conservation laws of potential Korteweg–de Vries equation. Nonlinear Dyn. (2017). doi:10.1007/s11071-017-3467-4

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Arts and Sciences, Uludag University, 16059, Bursa, Turkey

    Yakup Yıldırım & Emrullah Yaşar

Authors
  1. Yakup Yıldırım
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Emrullah Yaşar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emrullah Yaşar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yıldırım, Y., Yaşar, E. An extended Korteweg–de Vries equation: multi-soliton solutions and conservation laws. Nonlinear Dyn 90, 1571–1579 (2017). https://doi.org/10.1007/s11071-017-3749-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3749-x

Keywords

Search

Navigation